please help its my birthday!!
Part A: Estimate the y-intercept of the function. What does the intercept represent in this context?
Part B: What are the domain and range of this function?

Answers
Answer:
See Below
Step-by-step explanation:
a.) y-int = 1,000
The y-int represents the base (lowest) price of the antique at age 0
b.) 0 to 10 years = 500
30 to 40 years ≈ 2000
Domain: all real numbers
Range: y ≥ 1,000
Happy Birthday :)
Answer:
Part A —> y intercept is 1000
Y intercept represents the value in dollars
X intercept represents the age of antique
Part B
Domain —> (1000,+oo)
Range —> (1000,+00)
Explanation :
Domain is the set of x values (input)
Range is the set of y values (output)
Related Questions
is y=-3x+2 a function? why is it/is it not a function?
Answers
It is a function.
You can try plot the graph of that equation and then plot a vertical line. You will see that the graph will only intercept the vertical line only once. That is a function.
Or you can look at the equation. Functions have the equations that start with "y=". Rather say that if you see "y" only (not y² or y³ just only y) then that is mostly a function.
The manager of a computer retails store is concerned that his suppliers have been giving him laptop computers with lower than average quality. His research shows that replacement times for the model laptop of concern are normally distributed with a mean of 3.1 years and a standard deviation of 0.5 years. He then randomly selects records on 49 laptops sold in the past and finds that the mean replacement time is 2.9 years. Assuming that the laptop replacement times have a mean of 3.1 years and a standard deviation of 0.5 years, find the probability that 49 randomly selected laptops will have a mean replacement time of 2.9 years or less.
Answers
The probability that 49 randomly selected laptops will have a mean replacement time of 2.9 years or less can be calculated using the z-score and the standard normal distribution.
To find the probability, we first calculate the z-score using the formula:
z = (x - μ) / (σ / √n)
where x is the sample mean (2.9 years), μ is the population mean (3.1 years), σ is the population standard deviation (0.5 years), and n is the sample size (49 laptops).
Plugging in the values, we have:
z = (2.9 - 3.1) / (0.5 / √49)
z = -0.2 / (0.5 / 7)
z = -0.2 / 0.0714
z ≈ -2.80
Next, we use a standard normal distribution table or calculator to find the probability corresponding to the z-score of -2.80. The probability can be found as the area under the curve to the left of the z-score.
By calculating the z-score, we standardize the sample mean with respect to the population mean and standard deviation. This allows us to compare the sample mean to the population distribution.
The negative z-score indicates that the sample mean of 2.9 years is below the population mean of 3.1 years. By looking up the corresponding probability from the standard normal distribution, we find that it is very unlikely to obtain a sample mean of 2.9 years or less by chance alone.
To know more about z-scores , refer here:
https://brainly.com/question/31871890#
#SPJ11
a bicycle has an average speed of 8.00 km/h. how far will it travel in 10.0 seconds
Answers
The bicycle will travel approximately 0.022 kilometers in 10.0 seconds at an average speed of 8.00 km/h.
To calculate the distance traveled by a bicycle in 10.0 seconds with an average speed of 8.00 km/h, we need to convert the time from seconds to hours to match the unit of the average speed.
Given:
Average speed = 8.00 km/h
Time = 10.0 seconds
First, we convert the time from seconds to hours:
10.0 seconds = 10.0/3600 hours (since there are 3600 seconds in an hour)
10.0 seconds ≈ 0.0027778 hours
Now, we can calculate the distance using the formula:
Distance = Speed × Time
Distance = 8.00 km/h × 0.0027778 hours
Distance ≈ 0.0222222 km
Therefore, the bicycle will travel approximately 0.022 kilometers in 10.0 seconds at an average speed of 8.00 km/h.
For more questions on average speed
https://brainly.com/question/4931057
#SPJ8
Your answer should be at 50 or more words. You imagine that your tutor is asked to record the \D, student name, date of birth, home address and phone number of every student in your tutorial and then email the spreadsheet to the unit convenor. What problems might arise? Note: there are around 120 students in this, unit and several tutors. You must start a thread before you can read and reply to other threads
Answers
There are several potential problems that might arise if a tutor is asked to record personal information such as student names, dates of birth, home addresses, and phone numbers for a large number of students and then email the spreadsheet to the unit convenor.
One major concern is the security and privacy of the students' personal information.
There are logistical challenges involved in managing and organizing the large amount of data.
One major concern is the security and privacy of the students' personal information. Emailing a spreadsheet containing sensitive data poses a risk of unauthorized access, interception, or data breaches. If the spreadsheet falls into the wrong hands, it could lead to identity theft, privacy violations, or misuse of personal information. Additionally, there is the issue of compliance with data protection regulations, such as the General Data Protection Regulation (GDPR), which requires the protection of personal data and imposes strict guidelines on its handling.
Moreover, there are logistical challenges involved in managing and organizing the large amount of data. Ensuring accuracy and maintaining data integrity becomes increasingly difficult with a higher number of students and multiple tutors. There may be instances of data entry errors, missing information, or duplication, which can lead to confusion and inaccuracies in student records.
To address these problems, it is important to establish secure data management protocols, such as using encrypted file transfer methods or secure file sharing platforms. Implementing strict access controls and limiting the number of individuals handling and transmitting the data can help mitigate the risks. It is also essential to comply with relevant privacy laws and regulations and provide clear guidelines to tutors on data protection and confidentiality. Regular data audits and reviews can help identify and rectify any potential issues in the data management process.
Learn more about data integrity here:
https://brainly.com/question/33539122
#SPJ11
In parallelogram M NOP, PK = 5x and K N = n2 – 14.
What is PN?
A. 7
B. 36
C. 70
D. 100

Answers
Answer:
C.) 70
Step-by-step explanation:
The line PN is made up of PK and KN (PN = PK + KN). We also know that PK must equal KN (definition of a parallelogram). Therefore, you can set the value of both lines equal to each other, solve for x, then add them together to find PN.
PN = ?
PK = 5x
KN = n² - 14
PK = KN <----- Both lines must equal one another
5x = n² - 14 <----- Substitute values in
0 = n² - 5x - 14 <----- Subtract 5x from both sides
0 = (x - 7)(x + 2) <----- Factor
x = 7 x = -2 <----- Set both parentheses equal to 0
The value for "x" can be 7 and -2. However, it does not make sense to use a negative value in this situation. If we were to plug -2 into the equations, it would result in lines with a negative value. Therefore, "x" must be 7. Next, plug this value in for "x" to find the numerical value of PK and KN.
PK = 5x -----> 5(7) = 35
KN = n² - 14 -----> (7)² - 14 = 35
The fact that these are equal makes sense. Now, add these two numbers to find the value of the overall line.
PK + KN = PN
35 + 35 = 70
Therefore, C.) 70 is the value of PN.
answer both A and B please

Answers
Answer:
3 and - 10
Step-by-step explanation:
(a)
when x = 0 in the interval x ≤ 0 then y = \(\frac{3}{2}\) x + 3 , so
y = \(\frac{3}{2}\) (0) + 3 = 0 + 3 = 3
when x = 0, the value of the function is 3
(b)
when x = 5 in the interval x > 0 then y = - 2x , so
y = - 2(5) = - 10
when x = 5 the value of the function is - 10
Answer: a. when x=0, the value of the function is 3
b. when x=5, the value of the function is -10
Step-by-step explanation:
\(\displaystyle\\y=\left \{ {{\frac{3}{2}x+3,\ if\ x\leq 0 } \atop {-2x,\ if\ x > 0}} \right.\)
\(\displaystyle\\x=0\\\\Hence,\\\\y=\frac{3}{2} (0)+3\\\\y=0+3\\\\y=3\)
\(x=5\\\\Hence,\\\\y=-2(5)\\\\y=-10\)

Drag each number to show whether or not it is a solution to the inequality shown.
Inequality: 20≥5+3x

Answers
Answer:
solutions: -15, 4 3/4
not solutions: 10 2/3 and 129
Step-by-step explanation:
Let's solve the inequality first
\(20 \geqslant 5 + 3x \\ 20 - 5 \geqslant 3x \\ 15 \geqslant 3x \\ 5 \geqslant x\)
so solution set must contain all the values that are less than equal to 5.
-15 and 4 3/4 are less than 5
so these are solutions.
129 and 10 2/3 are bigger than 5. That means these are not solutions.
We are interested in the activity diagram. Check all the correct
answers.
Please select at least one answer.
O a. There can be multiple end points, but only one starting
point.
O b. Any joint must hav
Answers
The correct statements regarding activity diagrams are:
a. There can be multiple end points, but only one starting point.
c. A branch can have multiple incoming arrows.
d. A decision point may have more than 2 outgoing arrows.
e. An indeterminacy is created when the successors of an activity have non-mutually exclusive conditions.
f. An activity can be nested within another activity.
Activity diagrams are graphical representations used in software engineering to depict the flow of activities or actions within a system. The correct statements regarding activity diagrams are as follows:
a. There can be multiple end points, but only one starting point:
Activity diagrams typically illustrate the flow of activities from a single starting point to multiple end points. This allows for depicting different termination points in the system's behavior.
c. A branch can have multiple incoming arrows:
A branch in an activity diagram represents a decision point where the flow of activities can diverge. It is possible for multiple incoming arrows to converge at a branch, indicating different paths leading to the decision point.
d. A decision point may have more than 2 outgoing arrows:
A decision point in an activity diagram represents a condition or a decision that determines the subsequent flow of activities. It is possible for a decision point to have more than two outgoing arrows, indicating different paths based on the decision outcome.
e. An indeterminacy is created when the successors of an activity have non-mutually exclusive conditions:
In an activity diagram, if the subsequent activities following a certain action have conditions that are not mutually exclusive, it creates an indeterminacy. This means that multiple paths may be followed simultaneously based on the different conditions.
f. An activity can be nested within another activity:
Activity diagrams support the nesting of activities within each other. This allows for representing complex activities or sub-processes within a larger activity, providing a hierarchical structure to the diagram.
In conclusion, the correct statements regarding activity diagrams include multiple end points and a single starting point, the possibility of multiple incoming arrows at a branch, the presence of more than two outgoing arrows at a decision point, the creation of indeterminacy with non-mutually exclusive conditions, and the ability to nest activities within one another.
To learn more about Activity diagrams visit:
brainly.com/question/33456875
#SPJ11
We are interested in the activity diagram. Check all the correct answers.
Please select at least one answer.
O a. There can be multiple end points, but only one starting point.
O b. Any joint must have been preceded by a branch.
O c. A branch can have multiple incoming arrows.
O d. A decision point may have more than 2 outgoing arrows.
Oe. An indeterminacy is created when the successors of an activity have non-mutually exclusive conditions.
Of. An activity can be nested within another activity.
At a coffee shop, the amount of tax due is calculated based on the cost of the customer's
order.
t = the amount of tax due
c = the cost of the order
Which of the variables is independent and which is dependent?
Answers
In this context, the dependent variable is t (amount of tax due) and the independent variable is c (cost of the order).In this scenario, the variables are t (the amount of tax due) and c (the cost of the order).
To determine which variable is independent and which is dependent, we need to understand their relationship.In this case, the amount of tax due, t, is calculated based on the cost of the customer's order, c. The tax amount is dependent on the cost of the order because it is directly influenced by the value of c. As the cost of the order changes, the amount of tax due will also change accordingly.
On the other hand, the cost of the order, c, is independent. It is not influenced or determined by the amount of tax due. The customer can choose the cost of their order, and the tax will be calculated based on that chosen amount.
For more such questions on variable
https://brainly.com/question/27894163
#SPJ8
a lamina occupies the part of the disk x2 y2 ≤ 1 in the first quadrant. find its center of mass if the density at any point is proportional to its distance from the y-axis.
Answers
the center of mass of the lamina is (x_cm, y_cm) = (3/16, 3/16).
To find the center of mass of the lamina, we need to calculate the coordinates (x_cm, y_cm) where the mass is concentrated.
The density at any point is proportional to its distance from the y-axis. This implies that the density (ρ) at a point (x, y) is given by ρ = kx, where k is a constant of proportionality.
To find the center of mass, we need to integrate over the lamina's region to calculate the mass (M) and the moments (Mx and My) about the x and y axes, respectively. Then, we can use these values to find the coordinates of the center of mass.
Let's proceed with the calculations:
1. Finding the mass (M):
The mass element dm at a point (x, y) is given by dm = ρ * dA, where dA is the differential area element.
Since ρ = kx, we have dm = kx * dA.
To calculate the mass, we integrate this expression over the region of the lamina:
M = ∫∫ρ * dA
= ∫∫kx * dA
= k * ∫∫x * dA
The region of integration is the part of the disk x² + y² ≤ 1 in the first quadrant.
We can rewrite the bounds of integration as follows:
0 ≤ x ≤ 1 (since it's in the first quadrant)
0 ≤ y ≤ √(1 - x²) (using the equation of the disk)
Now, we can set up the double integral:
M = k * ∫[0 to 1]∫[0 to √(1 - x²)]x * dy * dx
2. Finding the moments (Mx and My):
The moments about the x and y axes are given by:
Mx = ∫∫x * ρ * dA
My = ∫∫y * ρ * dA
Using the same region of integration and density expression, we can set up the double integral for My:
My = k * ∫[0 to 1]∫[0 to √(1 - x²)]y * x * dy * dx
3. Calculating the center of mass:
The coordinates of the center of mass (x_cm, y_cm) are given by:
x_cm = Mx / M
y_cm = My / M
Now, we can evaluate the integrals to find the mass and moments, and then calculate the coordinates of the center of mass:
Step 1: Calculate the mass M
M = k * ∫[0 to 1]∫[0 to √(1 - x²)]x * dy * dx
M = k * ∫[0 to 1]x * √(1 - x²) dx
Let u = 1 - x²
du = -2x dx
When x = 0, u = 1
When x = 1, u = 0
M = -k * ∫[1 to 0]√u du
M = k * ∫[0 to 1]√u du
M = k * (2/3) * u³/² |[0 to 1)
M = k * (2/3) * (1 - 0)
M = k * 2/3
Step 2: Calculate the moment Mx
Mx = k * ∫[0 to 1]∫[0 to √(1 - x²)]x * y * dy * dx
Mx = k * ∫[0 to 1]x * ∫[0 to √(1 - x²)]y * dy * dx
Mx = k * ∫[0 to 1]x * (1/2) * y² |[0 to √(1 - x²)] dx
Mx = k * ∫[0 to 1]x * (1/2) * (1 - x²) dx
Mx = k * (1/2) * ∫[0 to 1](x - x³) dx
Mx = k * (1/2) * (x²/2 - x⁴/4) |[0 to 1]
Mx = k * (1/2) * (1/2 - 1/4)
Mx = k * (1/2) * (1/4)
Mx = k/8
Step 3: Calculate the moment My
My = k * ∫[0 to 1]∫[0 to √(1 - x²)]y * x * dy * dx
My = k * ∫[0 to 1]x * ∫[0 to √(1 - x²)]y * dy * dx
My = k * ∫[0 to 1]x * (1/2) * y² |[0 to √(1 - x²)] dx
My = k * ∫[0 to 1]x * (1/2) * (1 - x²) dx
My = k * (1/2) * ∫[0 to 1](x - x³) dx
My = k * (1/2) * (x²/2 - x⁴/4) |[0 to 1]
My = k * (1/2) * (1/2 - 1/4)
My = k * (1/2) * (1/4)
My = k/8
Step 4: Calculate the coordinates of the center of mass
x_cm = Mx / M = (k/8) / (k * 2/3) = 3/16
y_cm = My / M = (k/8) / (k * 2/3) = 3/16
Therefore, the center of mass of the lamina is (x_cm, y_cm) = (3/16, 3/16).
Learn more about Center of mass here
https://brainly.com/question/13125378
#SPJ4
Solve and graph the following inequality: x - 19 is less than or equal to 27
Answers
You have the following inequality:
x - 19 ≤ 27
To solve the previous inequality, add 19 both sides and simplify:
x ≤ 27 + 19
x ≤ 46
The graph is:

Answer:
x is less than or equal to 8
Step-by-step explanation:
Which graphs form a function? (Choose all that apply)

Answers
To find it out on a graph is the line test
Draw a line going up and down and if it only passes the line once it’s a function but if it touches the line more then once it is not
hurry please and thank you #4

Answers
Considering the figure, the equation AB rests is on
y = -2/3 x because y decreases by 6 units for every unit that x increases and -6/9 = -2/3What is linear function ?A linear function consists of functions where the variables has exponents of 1.
The graph of linear functions is a straight line graph and the relationship is expressed in the form.
y = mx + c
The slope is represented as m, The slope by definition is the ratio of change of the output values to the change in the input values. The slope can also be called the rate of change
How to find the equation for which line AB liesWhen a line slopes from top left to bottom right, the line is said to have a negative slope. This coincides with the line in the figure hence the line will have a negative slope.
There is not enough information to get the y intercept, hence the line will be
y = mx
where m = -6/9 = -2/3
therefore y = -2/3 x
Learn more about slope of linear functions at:
https://brainly.com/question/20277632
#SPJ1
b. What's the probability a customer who ordered pancakes came to the diner late?
c. Are breakfast choice and meal time independent? Explain.

Answers
Answer:
b. To find the probability a customer who ordered pancakes came to thediner late, we need to look at the intersection of the "pancakes" row and the "late" column. This gives us a probability of 0.1, or 10%
c. To determine whether breakfast choice and meal time are independent, we need to see if the probability of one event changes based on the occurrence of the other event. In this case, it seems that breakfast choice and meal time are not independent, as the probability of being late seems to differ based on what breakfast item the customer chose. For example, the probability of being late is higher for customers who ordered pancakes compared to those who ordered cereal. Therefore, the choice of breakfast item appears to be related to the probability of being late, and so breakfast choice and meal time are not independent.
Step-by-step explanation:
In statistical process control, when a point falls outside of control limits, the probability is quite high that the process is experiencing _____________ .
A. common cause variation
B. student t variation
C. a reduction of variables
D. special cause variation
Answers
When a point falls outside of control limits in statistical process control, the probability is quite high that the process is experiencing special cause variation.
In statistical process control (SPC), control limits are used to define the range within which a process is expected to operate under normal or common cause variation. Common cause variation refers to the inherent variability of a process that is predictable and expected.
On the other hand, special cause variation, also known as assignable cause variation, refers to factors or events that are not part of the normal process variation. These are typically sporadic, non-random events that have a significant impact on the process, leading to points falling outside of control limits.
When a point falls outside of control limits, it indicates that the process is exhibiting a level of variation that cannot be attributed to common causes alone. Instead, it suggests the presence of specific, identifiable causes that are influencing the process. These causes may include equipment malfunctions, operator errors, material defects, or other significant factors that introduce variability into the process.
Therefore, when a point falls outside of control limits in statistical process control, it is highly likely that the process is experiencing special cause variation, which requires investigation and corrective action to identify and address the underlying factors responsible for the out-of-control situation.
Learn more about statistical process control here:
https://brainly.com/question/32323372
#SPJ11
The base of a parallelogram is six more than twice the height. The height is 5 inches. What is the length of the base?
Answers
The length of the base of the parallelogram is 16 inches.
What is parallelogram?
A parallelogram is a four-sided plane figure with opposite sides parallel and congruent (having the same length). This means that the opposite sides of a parallelogram are parallel to each other and have the same length. Additionally, the opposite angles of a parallelogram are equal in measure, which means they have the same degree of rotation.
Let's use the information given in the problem to set up an equation and solve for the length of the base.
From the problem, we know that the height of the parallelogram is 5 inches.
h = 5
We also know that the base of the parallelogram is six more than twice the height. Let's use b to represent the length of the base:
b = 2h + 6
Now we can substitute the value we know for the height and solve for the base:
b = 2(5) + 6
b = 10 + 6
b = 16
Therefore, the length of the base of the parallelogram is 16 inches.
To learn more about parallelogram visit the link:
https://brainly.com/question/970600
#SPJ1
The vertex of this parabola is at (-3,6). Which of the following could be it's equation?
A. y=-3(x+3)2-6
B. y=-3(x-3)2-6
C. y=-3(x+3)+6
D. y=-3(x-3)+6
Answers
Answer:
y=3(x+3)2-6
rip nip kip
40+70+60+120=300
the answer is 300....
Equation that could be the equation of parabola with vertex (-3 , 6)
What is parabola?A parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point (known as the focus) and from a fixed straight line which is known as the directrix.
Given,
Vertex of parabola (h,k) = (-3, 6)
Vertex-form equation of parabola
y = a(x - h)² + k
y = a(x - -3)² + 6
y = a(x + 3)² + 6
Equation of the parabola should be of form
y = a(x + 3)² + 6
Hence, y = -3(x + 3)² + 6 is the equation that could be the equation of parabola with vertex (-3 , 6)
Learn more about parabola here:
https://brainly.com/question/21685473
#SPJ7
Question is the image :

Answers

Answer:
x can be any real number except -5 and 7
Step-by-step explanation:
x is in the denominator and denominator cannot be 0
so 6 - |x-1| cannot be 0
==> |x-1| cannot be 6
because it's absolute value, so
x-1 cannot be 6 & x-1 cannot be -6
which give us the answer x cannot be 7 and x cannot be -5
so the answer is x can be any real number except -5 and 7
Help asap will give briniest

Answers
The frequency of each interval is:
81-100: 2
61-80: 2
1-20: 1
21-40: 1
41-60: 2
What is frequency interval?
Frequency refers to the number of times a particular value or event occurs within a given dataset or sample. In statistics, frequency is used to describe the distribution of values in a dataset, and it is often represented as a frequency table or histogram.
Frequency is often used in conjunction with other statistical measures such as mean, median, and mode to describe the central tendency and variability of a dataset. By analyzing the frequency of values within a dataset, we can identify patterns and trends, and make inferences about the population from which the sample was drawn.
According to the question:
Using the given intervals, we can count the frequency of each interval as follows
81-100: 2 (81, 97)
61-80: 2 (65, 44)
1-20: 1 (2)
21-40: 1 (24)
41-60: 2 (25, 38)
Total: 8
To know more about frequency interval visit:
https://brainly.com/question/27425467
#SPJ1
A NACA 23012 airfoil with chord of 5 feet is placed in a subsonic wind tunnel for testing. The wind tunnel operates at standard sea-level conditions at Mach 0.25. The airfoil is placed at an angle of attack of 6
∘
. Determine; a) the zero lift angle of attack, b) lift (lb/ft) (per unit span), c) drag (lb/ft) (per unit span), and d) moment about the quarter chord (ft-lb/ft) (per unit span). Assume Re=6×10
6
for chart information. A NACA 4412 airfoil with a chord of 1.75 meters is placed in a subsonic wind tunnel for testing. The flow velocity, pressure, temperature, and viscosity are 45 m/s,1 atm,267 K, and 1.65×10
−5
kg/m−s, respectively. The airfoil is placed at an angle of attack of 2
∘
. Determine (per unit span); a) the lift, b) drag, and c) moment about the quarter chord. For the airfoil and flow conditions of problem #2 find the angle of attack necessary to produce 700 N per meter span of lift.
Answers
A NACA 4412 airfoil with a chord of 1.75 meters is placed in a subsonic wind tunnel for testing.
A NACA 23012 airfoil with a chord of 5 feet is placed in a subsonic wind tunnel for testing. The wind tunnel operates at standard sea-level conditions at Mach 0.25. The airfoil is placed at an angle of attack of 6°.
Given,
Re = 6 × 106
Since the airfoil is symmetrical, it will have a zero lift angle of attack of 0°.
a) The zero lift angle of attack is 0°.
From the graph, α ≈ 9°
Lift coefficient, Cl = 0.5
Drag coefficient, C
d = 0.02
b) Lift (lb/ft) (per unit span)
Lift coefficient, Cl = 0.5 Lift,
L = 0.5 × 0.002378 × 525 × 52 × 5Lift,
L = 30.95 lb/ft
c) Drag (lb/ft) (per unit span)
Drag coefficient,
Cd = 0.02
Drag, D = 0.02 × 0.002378 × 525 × 52 × 5
Drag, D = 2.02 lb/ft
d) Moment about the quarter chord (ft-lb/ft) (per unit span)
Moment coefficient, Cm = -0.0458
From the graph, α ≈ 9°
Cm = -0.0458
Moment,
M = -0.0458 × 0.002378 × 525 × 52 × (5 / 4)
Moment, M = -5.95 ft-lb/ft
A NACA 4412 airfoil with a chord of 1.75 meters is placed in a subsonic wind tunnel for testing.
The lift, drag, and moment coefficients were determined for two airfoils at different attack and flow conditions angles. The zero lift and angle of attack required to produce a given lift were also calculated.
To know more about the drag coefficient, visit:
brainly.com/question/31824604
#SPJ11
−3x+7y=5x+2yminus, 3, x, plus, 7, y, equals, 5, x, plus, 2, y Complete the missing value in the solution to the equation. (−5,(-5,(−5,left parenthesis, minus, 5, comma )))right parenthesis
Answers
Answer:
\((-5,-8).\)
Step-by-step explanation:
Given the equation
\(-3x+7y=5x+2y\)
We need to find the missing value of the coordinate; (-5, __)
First, we collect like terms
\(-3x-5x=2y-7y\\\\-8x=-5y\)
When x=-5
\(-8*-5=-5y\\\\40=-5y\)
Dividing both sides by -5
\(y=-8\)
The missing value of the coordinate (-5,y) is -8.
Thus, the complete solution to the equation is \((-5,-8).\)
simplify 3/5 x 1/4: fractions work
Answers
Answer:
\( \frac{3}{20} \)
Step-by-step explanation:
\( \frac{3}{5} \times \frac{1}{4} \)
\( = \frac{3 \times 1}{5 \times 4} \)
Simplify
\( = \frac{3}{20} \)
If you have any more questions please let me know.
Answer:
\($\large\boxed{\frac{3}{20} = 0.15} $\)
Step-by-step explanation:
\($\frac{3}{5} \cdot \frac{1}{4} = \frac{3 \cdot 1}{5 \cdot 4}=\frac{3}{20} = 0.15 $\)
in the linear equation y= 3/4x + 2 what does 2 represent?
Answers
Answer: The y intercept.
Step-by-step explanation:
Using the form y = mx +b, m represents the slope and b is the y intercept. In the equation y = 3/4x + 2, the slope (m) = 3/4 and the y intercept (b) = 2
Proportions
Find the unknown number in each proportion. 8
x days
4 years
=
365.25 days
1 year
9.
33,264 feet
x miles
5,280 feet
1 mile
Answers
Answer:
8 x 182.625 = 4years
Step-by-step explanation:
hard to understand the rest maybe upload a picture
Use the Distance Formula and the Pythagorean Theorem to find the distance between each pair of points. M (10, −4) and N (2, −7)
Answers
Answer:
\(d=\sqrt{73}\approx8.54\)
Step-by-step explanation:
So we have the two points (10,-4) and (2,-7).
And we want to find the distance between them using the Distance Formula and the Pythagorean Theorem. Let's do each one individually.
1) Distance Formula.
The distance formula is:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2\)
Let's let (10,-4) be (x₁, y₁) and let's let (2,-7) be (x₂, y₂). So:
\(d=\sqrt{((2)-(10))+((-7)-(-4))^2\)
Simplify:
\(d=\sqrt{(2-10)^2+(-7+4)^2\)
Subtract:
\(d=\sqrt{(-8)^2+(-3)^2\)
Square:
\(d=\sqrt{64+9}\)
Add:
\(d=\sqrt{73}\)
Approximate:
\(d\approx8.54\)
So, the distance between (10,-4) and (2,-7) is approximately 8.54 units.
2) Pythagorean Theorem
Please refer to the graph.
So, we want to find the distance. This will be the length of the red line, or the hypotenuse.
First, let's find the length of the two legs.
The longer leg will be the difference between the two x-coordinates. So, the length of the longer leg is:
\((10-2)=8\)
Note: It doesn't matter if we do 2-10, which gives -8, since we are going to square anyways. Also, distance is always positive, so 8 would be our answer.
And the shorter leg is the difference between the two y-coordinates. Namely:
\((-7-(-4))=-3=3\)
So, the shorter leg is 3 units.
So now, we can use the Pythagorean Theorem, which is:
\(a^2+b^2=c^2\)
Substitute 8 for a and 3 for b. So:
\((8)^2+(3)^2=c^2\)
Square:
\(64+9=c^2\)
Add:
\(c^2=73\)
Take the square root:
\(c=\sqrt{73}\approx8.54\)
This is the same as our previous answer, so we can confirm that it's correct.
So, using both the distance formula and the Pythagorean Theorem, the distance between the two points is approximately 8.54.
And we're done!

Distance formula: d = √(x2-x1)²+(y2-y1)²
= √(2-10)²+(-7-(-4))²
= √-8²+(-3)²
= √64+9
= √73
≈ 8.54
Best of Luck!
Evaluate the integral by making the given substitution. (Use C for the constant of integration.) ∫x 3
(9+x 4
) 6
dx,u=9+x 4
Answers
∫x³(9+x⁴)⁶dx = x⁻¹² [(1/8)(9 + x⁴)⁸ - (9/7)(9 + x⁴)⁷] + C
Given, ∫x³(9+x⁴)⁶dx
Let u = 9 + x⁴
Differentiating with respect to x, we getdu/dx = 4x³Or, dx = du/4x³
Putting the value of dx in the given integral, we get∫x³(9+x⁴)⁶dx= ∫(u - 9)u⁶(1/4x³)du= (1/4) ∫(u - 9)u⁶(x⁴)⁻³du= (1/4) ∫(u - 9)(x⁴)⁻³(u⁶)duLet I = ∫(u - 9)(x⁴)⁻³(u⁶)du
Therefore, I = ∫(u - 9)u⁶(x⁴)⁻³du= ∫(u - 9)x⁻¹²(u⁶)du
Taking x⁻¹² out of the integral, we getI = ∫(u - 9)x⁻¹²(u⁶)du= x⁻¹² ∫(u - 9)u⁶du
Taking the integral of (u - 9)u⁶, we getI = x⁻¹² [(1/8)u⁸ - (9/7)u⁷] + C
Putting the value of u, we getI = x⁻¹² [(1/8)(9 + x⁴)⁸ - (9/7)(9 + x⁴)⁷] + C
Therefore, ∫x³(9+x⁴)⁶dx = x⁻¹² [(1/8)(9 + x⁴)⁸ - (9/7)(9 + x⁴)⁷] + C
Learn more about: Differentiating
https://brainly.com/question/33342920
#SPJ11
If A and B are any two events defined on a sample space S of an experiment, then p(A ∩ B) = p(A).p(B)
True or False
Answers
The statement is True only for independent events and False otherwise. The statement "p (A ∩ B) = p(A). p(B)" is not always true for any two events A and B defined on a sample space S of an experiment.
This equation only holds true if A and B are independent events, meaning that the occurrence of one event does not affect the probability of the other event happening. In other words, p(A|B) = p(A) and p(B|A) = p(B).
If A and B are dependent events, meaning that the occurrence of one event affects the probability of the other event happening, then the equation does not hold true. In this case, the probability of A and B occurring together (p(A ∩ B)) would be less than the product of the probabilities of A and B occurring separately (p(A).p(B)).
Therefore, the statement is not always true and depends on whether A and B are independent or dependent events.
Learn more about experiment here:
brainly.com/question/28198971
#SPJ11
You are given \( f=10 \) meissurements: \( 3,5,4,6,10,5,6,9,2,13 \). (D) Calculate \( x_{2} \) \( \frac{2}{x}= \) (b) Firud m. \( m= \) (c) Find the mode. (If these is more than one mode, enter your answer
Answers
Two values have frequency 2, so both are modes. They are 5 and 6. Therefore, the mode is 5 and 6.
Given measure: 3, 5, 4, 6, 10, 5, 6, 9, 2, 13.(D) To calculate \(x_2\), first we need to sort the data in ascending order: 2, 3, 4, 5, 5, 6, 6, 9, 10, 13
Now, we need to find the median, which is the middle value of the data. Since the data has even number of values, we will calculate the mean of middle two values, that is:(5+6)/2 = 5.5 Therefore, \(x_2 = 5.5\).\( \frac{2}{x}= \) To find the value of x, we will first cross-multiply and then take the reciprocal of both sides:\[\frac{2}{x} = y \Rightarrow 2 = xy \Rightarrow x = \frac{2}{y}\] Therefore, \( \frac{2}{x}= \frac{2}{y}\).
(b) To calculate Fried m, we will use the formula: \[f_m = L + \frac{(n/2 - F)}{f} \times c\]where L is the lower limit of the modal class, F is the cumulative frequency of the class preceding the modal class, f is the frequency of the modal class, c is the class interval, and n is the total number of values.
First, we will calculate the class interval:c = (upper limit of class - lower limit of class) = (7-6) = 1 Next, we will construct a frequency table to find the modal class:| Class Interval | Frequency ||-------------------|------------|| 2-3 | 1 || 3-4 | 1 || 4-5 | 1 || 5-6 | 2 || 6-7 | 2 || 7-8 | 1 || 9-10 | 1 || 10-11 | 1 || 13-14 | 1 |The modal class is the class with highest frequency.
Here, two classes have frequency 2, so both are modes. They are 5-6 and 6-7.
Therefore, L = 5, F = 2, f = 2, n = 10, and c = 1. Substituting the values, we get:\[f_m = L + \frac{(n/2 - F)}{f} \times c = 5 + \frac{(10/2 - 2)}{2} \times 1 = 7\] Therefore, Fried m = 7.
(c) To find the mode, we look for the value(s) with highest frequency. Here, two values have frequency 2, so both are modes. They are 5 and 6. Therefore, the mode is 5 and 6.
To know more about modes visit:
brainly.com/question/33298559
#SPJ11
Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. cos 13π 15 cos − π 5 − sin 13π 15 sin − π 5 Find its exact value.
Answers
As per the addition formula, the value of the trigonometric function is -0.809.
In statistics, function is defined as a relationship between inputs where each input is related to exactly one output.
Here we have to find the value of the trigonometric function cos(13/15)cos(-/5)-sin(13/15)sin(-/5) by using the addition and subtraction formula.
Here we have the following trigonometric function:
=> cos(13/15)cos(-/5)-sin(13/15)sin(-/5)
Now, we have to use the trigonometric addition formula,
=> Cos (A+B) = Cos A Cos B - Sin A Sin B
To solve the given function,
Here let us rewrite the given function based on the addition formula, then we get,
=> Cos ( 13π/15 + (-π/5) )
=> Cos( 12π/5)
=> Cos(144°)
=> -0.809
To know more about function here.
https://brainly.com/question/10354322
#SPJ4
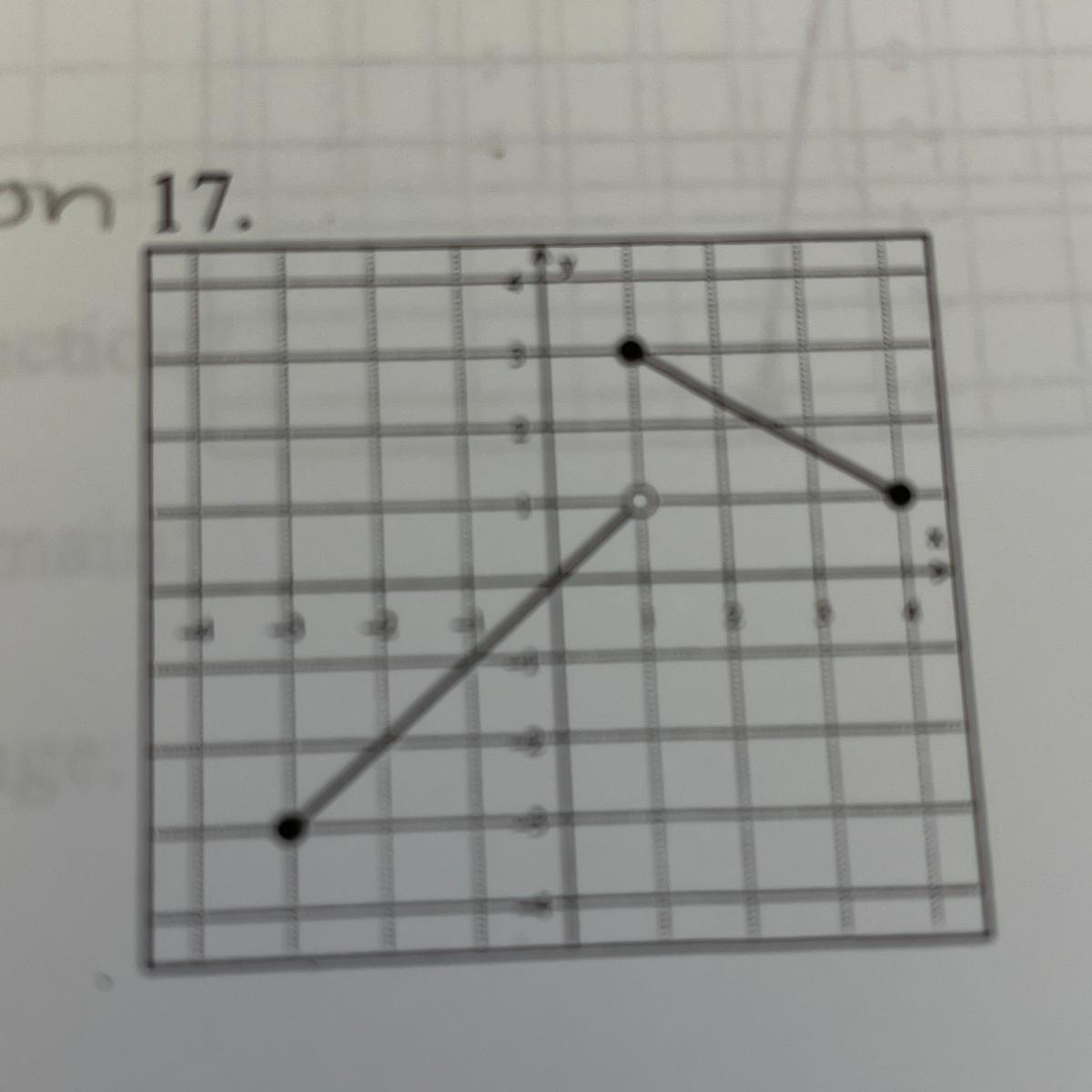
use the vertical line test to determine if the given relation is a function.