PLEASE HELP ILL GIVE BRAINLIEST AND 5 STARS AND THANKS!!!!! 60 POINTS!!!!
1) y= 2 x- 4 find parallel line through this point (-4,7)
2) y= -6x find parallel line through this point ( 4,9)
3) y= -½ x +3 find the perpendicular through this point ( 0,8)
4) y= -⅓ x find the perpendicular through this point (-2,1)
Answers
Answer:
1: y=2x+15
2: y=-6x+33
3: y=-1/2x+8
4: y=-\frac{1}{3}x+0.333
Step-by-step explanation:
Related Questions
find a vector equation of the line tangent to the graph of r(t) at the point p0 on the curve r(t)= (3t - 1) i + 13t j + 16 k; P0(-1, 4)
Answers
Vector equation of the line tangent to the graph of r(t) at the point p0 on the curve r(t) = (3t - 1) i + 13t j + 4 k.
What is the vector equation at the point P0(-1, 4)?To find a vector equation of the line tangent to the graph of r(t) at the point P0 on the curve r(t) = (3t - 1) i + 13t j + 16 k, where P0 is given as (-1,4), we can use the following steps:
Step 1: Find the derivative of r(t) with respect to t:
r'(t) = 3 i + 13 j
Step 2: Evaluate the derivative at the point P0:
r'(-1) = 3 i + 13 j
Step 3: Use the point P0 and the vector r'(-1) to form the vector equation of the tangent line:
r(t) = P0 + r'(-1) t
where t is a scalar parameter.
Plugging in the values, we get:
r(t) = (-1)i + 4j + (3i + 13j)t
Simplifying, we get:
r(t) = (3t - 1) i + 13t j + 4 k
Therefore, the vector equation of the line tangent to the graph of r(t) at the point P0 on the curve
r(t) = (3t - 1) i + 13t j + 16 k is
r(t) = (3t - 1) i + 13t j + 4 k.
Learn more about Tangent line
brainly.com/question/31326507
#SPJ11
by studying the diagram, state the solution of the system

Answers
In the graph, (3, -1)
a characteristic, usually a numerical value, which describes a sample is called a _______. a. parameter b. statistic C. constant d. variable
Answers
Answer: B. statistic
Step-by-step explanation: A characteristic, usually a numerical value, which describes a sample, is called a statistic.
math help please help

Answers
You purchased a five-pack of new light bulbs that were recalled because % of the lights did not work. What is the probability that at least one of your lights is defective?.
Answers
The probability that at least one of the lights is defective is 0.2661 .
in the question ,
it is given that
the total number of bulbs in the pack of new light bulbs is (n) = 5
percent of bulb that did not work is = 6%
probability that lights did not work is (p) = 0.06
probability that lights work is (q) = 1 - 0.06 = 0.94
let x be the number of defective lights
So ,the probability that at least one of your lights is defective
is P(x ≥ 1) = 1 - P(x<1)
= 1 - P(x = 0)
By Binomial Probability
= 1 - ⁿCₓ*(p)ˣ*(q)ⁿ⁻ˣ
= 1 - ⁵C₀*(0.06)⁰*(0.94)⁵⁻⁰
= 1 - 1*1*(0.94)⁵ ...because ⁵C₀ = 1
= 1 - (0.94)⁵
= 1 - 0.7339
= 0.2661
Therefore , The probability that at least one of the lights is defective is 0.2661 .
The given question is incomplete , the complete question is
You purchased a five-pack of new light bulbs that were recalled because 6% of the lights did not work. What is the probability that at least one of your lights is defective ?
Learn more about Probability here
https://brainly.com/question/28788900
#SPJ4
The circumference of a circle is 29x inches. Find the radius.
Step 2 of 3: Without substitution, solve the formula for the unknown variable in terms of the known variables.
Answers
Answer:
r = \(\frac{29x}{2\pi }\)
x = \(\frac{2\pi r}{29}\)
Step-by-step explanation:
C = 2\(\pi\)r
29x = 2\(\pi\)r --------- (i)
divide both sides of (i) by 2\(\pi\)
r = \(\frac{29x}{2\pi }\)
but when you divide both sides of (i) by 29, you get
x = \(\frac{2\pi r}{29}\)
Last week, Clay wrote 4 checks for $20 each from his checking account and
made one deposit of $96. What was the change in the balance of his account
over the week?*
Answers
Answer:
Step-by-step explanation:
clay will have
-80+96=16 dollars
the change in balance is +16
help appreciated thanks

Answers
Answer:
No
Step-by-step explanation:
x=(b-5)/c≠(5-b)/c
supposedly
b=6
c=1
x=6-5/1=1
x=5-6/1= -1
1≠ -1
Answer:
No
Step-by-step explanation:
x = b - 5 / L equal to - (5 - b) / L
If ∬_Df(X,Y)DA≥0, Then F(X,Y)≥0 For All (X,Y) In D True or False
Answers
The correct answer is False. The non-negativity of the double integral does not guarantee that the function itself is non-negative for all points in the region.
The inequality ∬_Df(X,Y)DA ≥ 0 represents the condition that the double integral of the function f(X, Y) over the region D is greater than or equal to zero. This means that the net "signed" area under the surface defined by the function f(X, Y) over the region D is either positive or zero.
However, this condition does not imply that the function f(X, Y) itself is non-negative (greater than or equal to zero) for all points (X, Y) within the region D. The function f(X, Y) may take both positive and negative values at different points in D, as long as the overall integral over the region is non-negative.
To illustrate this, consider a simple example where the region D is a circular disk centered at the origin. Let's assume that the function f(X, Y) is defined as f(X, Y) = X - Y. In this case, f(X, Y) can take negative values within the disk, but the double integral ∬_Df(X,Y)DA could still be non-negative if the positive and negative contributions balance out.
So, while the non-negativity of the double integral guarantees that the net signed area is non-negative over the entire region, it does not guarantee that the function itself is non-negative for all points in the region. Therefore, the statement "F(X,Y) ≥ 0 for all (X,Y) in D" is not necessarily true.
To learn more about inequality click here: brainly.com/question/20383699
#SPJ11
please help in the math
\( \frac{x + y}{x - y} + \frac{x - y}{x + y} - \frac{2( {x}^{2} - {y}^{2}) }{ {x}^{2} - {y}^{2} } \)
Answers
Answer:
\( \rm \displaystyle \frac{x + y}{x - y} + \frac{x - y}{x + y} - \frac{2( {x}^{2} - {y}^{2}) }{ {x}^{2} - {y}^{2} } = \boxed{ \displaystyle \frac{4y ^2}{(x - y)(x + y)} }\)
Step-by-step explanation:
we want to simplify the following
\( \rm \displaystyle \frac{x + y}{x - y} + \frac{x - y}{x + y} - \frac{2( {x}^{2} - {y}^{2}) }{ {x}^{2} - {y}^{2} }\)
notice that we can reduce the fraction thus do so:
\( \rm \displaystyle \frac{x + y}{x - y} + \frac{x - y}{x + y} - \frac{2 \cancel{( {x}^{2} - {y}^{2}) }}{ \cancel{{x}^{2} - {y}^{2} }}\)
\( \rm \displaystyle \frac{x + y}{x - y} + \frac{x - y}{x + y} - 2 \)
in order to simplify the addition of the algebraic fraction the first step is to figure out the LCM of the denominator and that is (x-y)(x+y) now divide the LCM by the denominator of very fraction and multiply the result by the numerator which yields:
\( \rm \displaystyle \frac{x + y}{x - y} + \frac{x - y}{x + y} - 2 \\ \\ \displaystyle \frac{(x + y)^2 + (x - y)^2 - 2(x + y)(x - y)}{(x - y)(x + y)} \)
factor using (a-b)²=a²+b²-2ab
\( \rm \displaystyle \frac{(x + y-(x - y) )^2}{(x - y)(x + y)} \)
remove parentheses
\( \rm \displaystyle \frac{(x + y-x + y) )^2}{(x - y)(x + y)} \)
simplify:
\( \rm \displaystyle \frac{4y ^2}{(x - y)(x + y)} \)
9514 1404 393
Answer:
4y²/(x² -y²)
Step-by-step explanation:
The expression simplifies as follows:
\(\dfrac{x+y}{x-y}+\dfrac{x-y}{x+y}-\dfrac{2(x^2-y^2)}{x^2-y^2}\\\\=\dfrac{(x+y)(x+y)+(x-y)(x-y)-2(x^2-y^2)}{(x-y)(x+y)}\\\\=\dfrac{(x+y)^2+(x-y)^2-2(x^2-y^2)}{x^2-y^2}\\\\=\dfrac{(x^2+2xy+y^2)+(x^2-2xy+y^2)-2(x^2-y^2)}{x^2-y^2}\\\\=\dfrac{2(x^2+y^2-(x^2-y^2))}{x^2-y^2}=\boxed{\dfrac{4y^2}{x^2-y^2}}\)
Una tienda ofrece descuentos en todos sus productos en el mismo porcentaje. Camila compró una silla de playa que costaba $26.970, pero pagó $21.576. Si además por un quitasol pagó $15.992. ¿Cuál era el precio original de este?
Answers
Answer:
Step-by-step explanation:
A store offers discounts on all its products at the same percentage. Camila bought a beach chair that cost $ 26,970, but paid $ 21,576. If he also paid $ 15,992 for a sunshade. What was the original price of this one?
Step 1
Find the percentage discount
% discount = Discount amount/ Original amount × 100
= $26,970 - $ 21,576/$26,970 × 100
= 0.2 × 100
= 20%
what is the range for the function f(x) = x2 – 9?
Answers
Answer:
In D=(−∞,−3]∪[3,+∞), the range of x→x2−9 is [0,+∞).
Step-by-step explanation:
Which equation represents a line which is perpendicular to the line y=2x-5y
A. 2x−y=−4
B. 2y−x=4
C. x+2y=-6
D.2x+y=-2
Answers
Answer:
c
Step-by-step explanation:
To find a perpendicular line, you must compare the slopes. With the equation y=2x-5, we're looking for the inverse/opposite slope of -1/2.
Option A still has a slope of 2. Option B, when everything is in the format of mx+b = y format is -x-4=-2y. which gives us 1/2 but not -1/2. C when everything is on the right side gives us -2y=x-6. Divide both sides by -2 to get the y by itself and you're left with y = -1/2x+3. Now we found the equation that gives us the -1/2 slope we were looking for.
heyy! i’ll give brainliest please help.

Answers
Answer:
the city at a lower altitude would have a colder climate
The quadratic functions f(x) and g(x) are described in the table.
x f(x) g(x)
−2 4 64
−1 1 49
0 0 36
1 1 25
2 4 16
3 9 9
4 16 4
5 25 1
6 36 0
In which direction and by how many units should f(x) be shifted to match g(x)?
A. Left by 18 units
B. Right by 18 units
C. Left by 6 units
D. Right by 6 units
Answers
The direction and by how many units should f(x) be shifted to match g(x) is Left by 6 units. Option C
How to determine the direction and by how many units should f(x) be shifted to match g(x)To determine the direction and magnitude of the shift needed for f(x) to match g(x), we can compare the corresponding values of f(x) and g(x) in the table.
For x = -2, f(x) = 4 and g(x) = 64.
For x = -1, f(x) = 1 and g(x) = 49.
For x = 0, f(x) = 0 and g(x) = 36.
For x = 1, f(x) = 2 and g(x) = 25.
For x = 2, f(x) = 4 and g(x) = 16.
By comparing the values, we can observe that the graph of f(x) is shifted to the right compared to g(x). To match the graph of g(x), we need to shift f(x) to the left.
The magnitude of the shift can be determined by the difference in x-values between the corresponding points of f(x) and g(x).
Learn more about magnitude at https://brainly.com/question/30337362
#SPJ1
The smiths purchased a house for $257,000. They sold their home for $350,000. What was the percent markup to the nearest percent?
Answers
Answer:
54%
Step-by-step explanation:
You used a student deck of 52 cards and selected a card at random find (c) 2 of heart
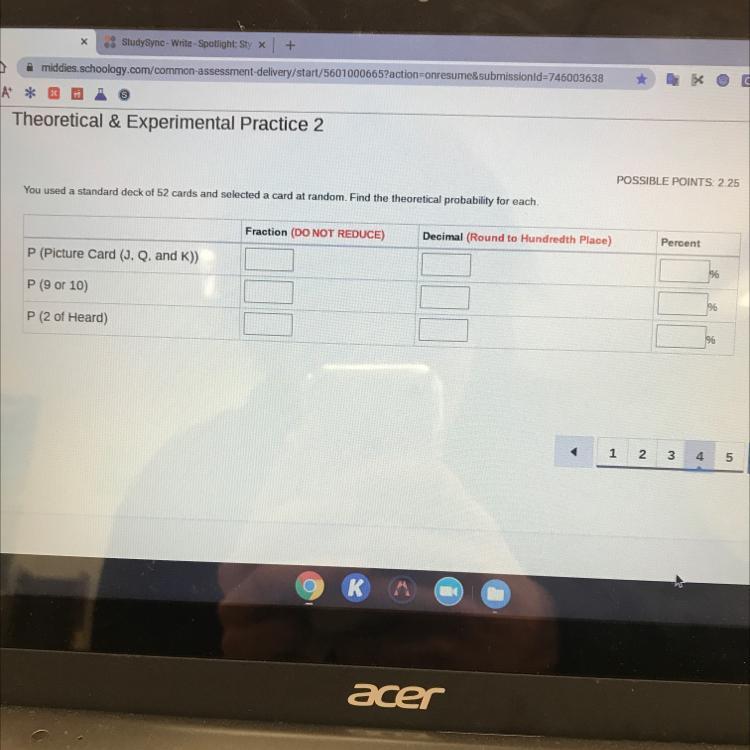
Answers
Definition
Theoretical Probability is the ratio of the number of favorable outcomes to the total possible outcomes of an event.
Expressing probability as a formula:
\(\text{probability = }\frac{Number\text{ of favorable outcomes}}{Total\text{ possible outcomes of an event}}\)Information about a standard deck of cards:
A standard deck of cards has four suits: hearts, clubs, spades, diamonds. Each suit has thirteen cards: ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, and king. Thus the entire deck has 52 cards total.
(a) Picture card (J, Q, and K)
In a standard deck, there are 4 Jacks, Queens, and Kings. Hence, the probability of J, Q, and K are:
\(\begin{gathered} \text{Number of picture cards = 4 }\times\text{ 3} \\ =\text{ 12} \end{gathered}\)Probability as a fraction:
\(=\text{ }\frac{12}{52}\)In decimal:
\(=\text{ }0.23\)Percent:
\(\begin{gathered} =\text{ 0.23 }\times\text{ 100} \\ =\text{ 23\%} \end{gathered}\)(b) 9 or 10
There are 4 cards labeled 9 and 10 each.
Probability as a fraction:
\(\begin{gathered} P(9or10)=\text{ P(9) + P(10)} \\ =\text{ }\frac{4}{52}\text{ + }\frac{4}{52} \\ =\text{ }\frac{8}{52} \end{gathered}\)In decimal:
\(=\text{ 0.15}\)In percent:
\(\begin{gathered} =\text{ 0.15 }\times\text{ 100} \\ =\text{ 15\%} \end{gathered}\)(c) 2 of heart
In a standard deck of cards, there are only one 2 of hearts.
Probability as a fraction:
\(=\text{ }\frac{1}{52}\)In decimal:
\(=\text{ 0.02}\)In percent:
\(\begin{gathered} =\text{ 0.02 }\times\text{ 100} \\ =\text{ 2\%} \end{gathered}\)A bag contains 50 tokens: 20 pink ,13 blue and 17 purble.if a person selects one token, replaces it,and then selects a second token,what is the probability of selecting 2 of the same colour
Answers
Answer:
Step-by-step explanation:
this is independent
20/50= 2/5= 40% of getting pink, probability of getting 2= 20%
13/50=0.26= 26% of getting blue, probability of getting 2= 13%
17/50=0.34=34% of getting purple, probability of getting 2 = 17%
70%
a. The opposite of
7/19
Answers
If the two figures are congruent, which statement is true?
A. BCDA ≅ FEHG
B. ABCD ≅ EFGH
C. BADC ≅ EFGH
D. ADCB ≅ HGFE

Answers
Answer:
A
Step-by-step explanation:
the order of letter should resemble the same shape
Andros has an oil fired heating system. In 30 days period he used a full tank of oil at a constant rate per day . At a different time of the year the amount of oil andros uses per day is 1/3 of the rate used in 30 days period . How many days should a full tank of oil last at this new rate
Answers
Answer:
90 days
Step-by-step explanation:
Let the rate per day for the 30 days period be x
Given that the rate drops to 1/3 of the rate used in 30 days period, it means that the new rate
= 1/3 x
If at a rate of x, the full tank runs for 30 days
at a rate of 1/3 x, the full tank would run for
= x/ (1/3 x) * 30 days
= 3 * 30 days
= 90 days
At the new rate, the full tank of oil will last for 90 days
a radio station gives a pair of concert tickets to the th correct caller who knows the birthday of the performer. for each person who calls, the probability is of knowing the performer's birthday. all calls are independent. define to be the number of calls needed to find a winner. (a) is a random variable. that is, identify the type of random variable and its parameter(s). (b) what is the probability that the th caller wins the tickets? (c) what is the probability that the station will need or more calls to find a winner?
Answers
The likelihood that the station will need 13 or more calls to determine a winner is 0.5 because each call is independent.
What is independent?Events A and B are considered to be independent events if their likelihood of occurring does not change as a result of the possibility that A will occur. P(A) = P(AB) = 1/2, which suggests that the likelihood of event. A occurring has not changed as a result of event B's happening. A pair of occurrences is considered independent if the occurrence of one does not change the likelihood that the other will also occur. The likelihood of both A and B happening is equal to the product of the probabilities of A and B (i.e., P), which is how mathematics expresses the independence of events A and B. (A and B)To learn more about independent, refer to:
https://brainly.com/question/25223322
#SPJ1
Suppose we choose a sample of size 100 from a population of monthly cable bills having standard deviation $20. If we assume the population mean bill is $65, what is the probability mean of our sample is greater than $70
Answers
The probability that the mean of our sample is greater than $70 is 0.62 or 62%.
How to obtain the probabilityThe probability of an event occurring is obtained by dividing the number of expected outcomes by the total number of events. In the question provided, we have a normal distribution, which means that we need the z score and this is gotten with the formula:
z = X - μ/σ
= 70 - 65/2
= 2.5
Now we find the P value for 2.5 and this is 0.9938
1 - 0.9938
= 0.0062
= 62%
Learn more about probability here:
https://brainly.com/question/24756209
#SPJ4
What is the area of the shaded region?

Answers
Answer: 12 cm^2
Step-by-step explanation:
Find area of small square = 2x2 = 4cm^2
Find Area of Big Square = 4x4 = 16cm^2
Area of Shaded Region = Area of Big Square - Area of small square = 16 - 4 = 12cm^2
What is the area of the parallelogram?

Answers
If you flip the other triangle and snap it together with the other triangle, you get a square so just do 8 times 7
(1) Find the volume in the first octant bounded by y^2=4−x and y=2z
(2) Find the volume bounded by z=x^2+y^2and z=4
Answers
the volume in the first octant bounded by\(y^2=4−x\) and y=2z is pi/36 sqrt(3).
(1) To find the volume in the first octant bounded by the surfaces \(y^2 = 4 - x\) and y = 2z, we can set up a triple integral in cylindrical coordinates.
First, we need to determine the bounds for our variables. Since we are working in the first octant, we know that 0 <= z, 0 <= theta <= pi/2, and 0 <= r.
Next, we need to find the equation for the upper and lower bounds of z in terms of r and theta. We can start with the equation \(y^2 = 4 - x\) and substitute y = 2z to get:
\((2z)^2 = 4 - x\)
\(4z^2 = 4 - x\)
\(x = 4 - 4z^2\)
We can then use this equation along with the equation z = y/2 to get the bounds for z:
\(0 < = z < = (4 - x)^(1/2)/2 = (4 - 4z^2)^(1/2)/2\)
Squaring both sides, we get:
\(0 < = z^2 < = (1 - z^2)/2\)
\(0 < = 2z^2 < = 1 - z^2\)
\(z^2 < = 1/3\)
So the bounds for z are:
\(0 < = z < = (1/3)^(1/2)\)
Finally, we can set up the triple integral in cylindrical coordinates:
V = ∫∫∫ r dz dtheta dr
with bounds:
0 <= r
0 <= theta <= pi/2
\(0 < = z < = (1/3)^(1/2)\)
and integrand:
r
So the volume in the first octant bounded by y^2=4−x and y=2z is:
V = ∫∫∫ r dz dtheta dr
= ∫ from 0 to\((1/3)^(1/2) ∫ from 0 to pi/2 ∫ from 0 to r r dz dtheta dr\)
= ∫ from 0 to\((1/3)^(1/2) ∫ from 0 to pi/2 r^2/2 dtheta dr\)
= ∫ from 0 to\((1/3)^(1/2) r^2 pi/4 dr\)
\(= pi/12 (1/3)^(3/2)\)
= pi/36 sqrt(3)
Therefore, the volume in the first octant bounded by\(y^2=4−x\) and y=2z is pi/36 sqrt(3).
(2) To find the volume bounded by z = x^2 + y^2 and z = 4, we can use a triple integral in cylindrical coordinates.
First, we need to determine the bounds for our variables. Since we are working in the region where z is bounded by \(z = x^2 + y^2\) and z = 4, we know that 0 <= z <= 4.
Next, we can rewrite the equation \(z = x^2 + y^2\) in cylindrical coordinates as \(z = r^2.\)
So the bounds for r and theta are:
0 <= r <= 2
0 <= theta <= 2pi
And the bounds for z are:
\(r^2 < = z < = 4\)
Finally, we can set up the triple integral in cylindrical coordinates:
V = ∫∫∫ r dz dtheta dr
with bounds:
0 <= r <= 2
0 <= theta <= 2pi
\(r^2 < = z < = 4\)
and integrand: 1
To know more about cylindrical coordinates, refer here:
https://brainly.com/question/30394340
#SPJ11
the length of a regtangle is 3 times the width. the perimeter is 3 times the width. the perimeter is 96 cm. find the width and length
Answers
In a rectangle where the length is 3 times the width, and the perimeter is 3 times the width. The perimeter is 96 cm, the length is 36 cm and the width is 12 cm.
Given,
Length of a rectangle is 3 times the width.
Perimeter is 3 times the width.
Perimeter is 96 cm.
Let w be the width of the rectangle.
The length of the rectangle is 3 times the width, so the length l is 3w.
The perimeter of the rectangle is equal to the sum of all its sides, so:
2w + 2(3w) = 96
2w + 6w = 96
8w = 96
w = 12
Therefore, the length is 36 cm and the width is 12 cm.
To know more about Perimeter refer here:
https://brainly.com/question/6465134
#SPJ11
Use Trigonometric substitution to eliminate the roots 1.1. 164+2 + 1 Use Trigonometric substitution to eliminate the roots 1.1. V64+2 + 1 1.2. V4z2 – 49
Answers
To eliminate the roots in 1.1 and 1.2, we can use trigonometric substitution. In 1.1, we can substitute x = 4 sin(theta) to eliminate the root of 4. In 1.2, we can substitute z = 7 sin(theta) to eliminate the root of 7.
1.1. V64+2 + 1 We can substitute x = 4 sin(theta) to eliminate the root of 4. This gives us:
V64+2 + 1 = V(16 sin^2(theta) + 2 + 1) = V16 sin^2(theta) + V3 = 4 sin(theta) V3 1.2. V4z2 – 49
We can substitute z = 7 sin(theta) to eliminate the root of 7. This gives us:
V4z2 – 49 = V4(7 sin^2(theta)) – 49 = V28 sin^2(theta) – 49 = 7 sin(theta) V4 – 7 = 7 sin(theta) (2 – 1) = 7 sin(theta)
Here is a more detailed explanation of the substitution:
In 1.1, we know that the root of 4 is 2. We can substitute x = 4 sin(theta) to eliminate this root. This is because sin(theta) can take on any value between -1 and 1, including 2.
When we substitute x = 4 sin(theta), the expression becomes V64+2 + 1 = V(16 sin^2(theta) + 2 + 1) = V16 sin^2(theta) + V3 = 4 sin(theta) V3
In 1.2, we know that the root of 7 is 7/4. We can substitute z = 7 sin(theta) to eliminate this root. This is because sin(theta) can take on any value between -1 and 1, including 7/4.
When we substitute z = 7 sin(theta), the expression becomes: V4z2 – 49 = V4(7 sin^2(theta)) – 49 = V28 sin^2(theta) – 49 = 7 sin(theta) V4 – 7 = 7 sin(theta)
To know more about root click here
brainly.com/question/16880173
#SPJ11
The original version of a song is 3 minutes long. The remix is 25% shorter. How long is the remix?
Answers
Answer = 2 minutes and 15 seconds
1 minute = 60 seconds
60 seconds times 3= 180 seconds
25% of 180 seconds = 45 seconds
180-45=135 seconds
convert into minutes
1 minute = 60 seconds
2 minutes = 120 seconds
135-120=15 seconds
2 minutes and 15 seconds
Answer:
2 mins 15 secs
Step-by-step explanation:
If the original version of the song is 100% in length, then the remix will be 75% of the length of the original, as:
100% - 25% = 75%
Convert 75% into a decimal:
⇒ 75% = 75/100 = 0.75
75% of 3 minutes
= 0.75 × 3
= 2.25 minutes
As there are 60 seconds in a minute,
= 0.25 of a minute = 0.25 × 60 = 15 seconds
Therefore, the length of the remix is 2 mins 15 secs
Please give the proof process: 2n3 + 3n +10 = Q( n³).
Answers
2n^3 + 3n + 10 can be written as a polynomial of the form Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3).
To prove that the expression 2n^3 + 3n + 10 is in the set Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3), we need to show that the expression can be written in the form a(n^3) for some constant "a".
Let's start by factoring out the common factor of n^3 from each term:
2n^3 + 3n + 10 = n^3(2 + 3/n^2 + 10/n^3)
Now, let's rewrite the expression as a single term multiplied by n^3:
2n^3 + 3n + 10 = (2 + 3/n^2 + 10/n^3)n^3
Simplifying the expression inside the parentheses:
= (2n^3 + 3n^2 + 10n^3)/n^3
= (12n^3 + 3n^2)/n^3
= 12 + 3/n
ow, we can see that the expression can be written in the form a(n^3), where a = 12 and n^3 = 3/n.
Therefore, we have shown that 2n^3 + 3n + 10 can be written as a polynomial of the form Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3).
Learn more about polynomial here
https://brainly.com/question/30478639
#SPJ11