PLEASE HELP, I WILL GOVE BRAINLIEST. Katrina's cat weighed 12 3/4 pounds at its last visit to the veterinarianSince that visit, the cat has gained 5/8 pound. How much does Katrina's cat weigh now? Show your work
Answers
Answer
13 1/2 pounds
Step-by-step explanation:
welcome ;)
Answer:
the cat now weighs 13 3/8 LBS
Step-by-step explanation:
convert the fractions so you can add them together,
mult 3/4 by two to get common denominators
6/8 + 5/8
the cat gained 11/8 pounds. (1 3/8)
since the numerator is larger we add the mixed number to the 12 pounds.
13 3/8 pounds.
Related Questions
how do you convert 3% into a decimal
Answers
Answer:
0.03
Step-by-step explanation:
Explanation: 3% is 3100 . so all you have to do is calculating 3100 ; which is 0.03 (skipping 2 decimal places from the number 3 to the left).
Answer:
explanation: we also convert 3/100 the answer is 0.03
11 less than the quotient of
4
44 and
�
xx.
Answers
The expression which is used to represents the statement "one-more than the quotient of a number x" and 4 is "x/4 + 1".
A "Quotient" is the result of a division operation between two numbers, where one number is divided by another. It represents the number of times one number is contained within another number.
An "Expression" is defined as "mathematical-phrase" which contain numbers, variables, and operators such as addition, subtraction, multiplication, and division. It can also contain functions and other mathematical symbols.
The quotient of a number"x" and 4 can be written as x/4.
So, one more than the quotient of a number x and 4 can be represented by the expression:
⇒ x/4 + 1,
Therefore, required mathematical expression is "x/4 + 1".
Learn more about Expression here
https://brainly.com/question/30553495
#SPJ1
The given question is incomplete, the complete question is
Write an expression to represent : One more than the quotient of a number x and 4.
A drum of water is 3/4 full. When 9 litres are drawn from it, it is half full. How much water does the drum hold what is the capacity of the drum
Answers
Answer:
OK, Here is your answer
Step-by-step explanation:
Let's assume the capacity of the drum be C litres.Since the drum is initially 3/4 full, the amount of water in it is 3/4 × C = (3/4)C liters.When 9 liters of water are drawn from the drum, the remaining amount of water is (3/4)C - 9 liters.Since the drum is now half full, the amount of water remaining in it is (1/2)C liters.Therefore, we can write the equation: (3/4)C - 9 = (1/2)CTo solve for C, let's first get rid of the fractions by multiplying both sides by 4.(3/4)C - 9 = (1/2)C → 3C - 36 = 2C → C = 36Therefore, the capacity of the drum is 36 liters.Hence, the drum holds 3/4 × 36 = 27 liters of water initially and after 9 liters of water are drawn, the remaining amount of water in it is 27 - 9 = 18 liters.
Answer:
18 Lieters.
Step-by-step explanation:
found the answer in his answer. ↑↑↑↑
5m - 12 = 2m + 6 + 3m
Answers
Bananas are selling for $0.85 a pound. Milan spent $9.86 on bananas. How many pounds of bananas did Milan buy?
Answers
Answer:
11.6 lbs
Step-by-step explanation:
Lavage Rapide is a Canadian company that owns and operates a large automatic car wash facility near Montreal. The following table provides estimates concerning the company’s costs:
Fixed Cost per Month Cost per Car Washed
Cleaning supplies $ 0.80
Electricity $ 1,400 $ 0.08
Maintenance $ 0.20
Wages and salaries $ 4,700 $ 0.40
Depreciation $ 8,000
Rent $ 2,100
Administrative expenses $ 1,400 $ 0.05
Answers
Lavage Rapide's total cost per car washed is $19.05.
What is equation?An equation in mathematics is a statement that states the equality of two expressions. An equation is made up of two sides that are separated by an algebraic equation (=). For example, the argument "2x + 3 = 9" asserts that the phrase "2x Plus 3" equals the value "9." The purpose of equation solving is to determine the value or values of the variable(s) that will allow the equation to be true. Equations can be simple or complicated, regular or nonlinear, and include one or more elements. The variable x is raised to the second power in the equation "x2 + 2x - 3 = 0." Lines are utilised in many different areas of mathematics, such as algebra, calculus, and geometry.
Fixed costs are expenses that do not change based on the number of units produced or sold. Variable costs, on the other hand, change with the level of production or sales. Here, the fixed costs are cleaning supplies, electricity, maintenance, wages and salaries, depreciation, rent, and administrative expenses.
The variable cost is the cost per car washed, which includes wages and salaries and administrative expenses.
To calculate the total cost per car washed, we need to add fixed costs to the variable cost per car. So, the total cost per car washed for Lavage Rapide would be:
Total Cost per Car Washed = Fixed Costs + Variable Cost per Car Washed
Total Cost per Car Washed =\(($0.80 + $1,400 + $0.20 + $4,700 + $8,000 + $2,100 + $1,400) + ($0.40 + $0.05)\)
Total Cost per Car Washed = $18,620 + $0.45
Total Cost per Car Washed = $19.05
Therefore, Lavage Rapide's total cost per car washed is $19.05.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
complete question:
Fixed Cost per Month Cost per Car Washed
Cleaning supplies $ 0.80
Electricity $ 1,400 $ 0.08
Maintenance $ 0.20
Wages and salaries $ 4,700 $ 0.40
Depreciation $ 8,000
Rent $ 2,100
Administrative expenses $ 1,400 $ 0.05
75 % of the students are boys . There are 24 boys . What is the total number of Students
PLEASE HELLPPPPPO
Answers
Answer:
32 students
Step-by-step explanation:
24 divided by .75 is 32
Based on the information given, there'll be 32 students.
Let the total number of students be represented by x.
From the information, it was stated that 75% of the students are boys and that there are 24 boys. Therefore, the total number of students will be:
75% × x = 24
0.75x = 24
x = 24/0.75
x = 32
There are 32 students.
Learn more about percentages on:
https://brainly.com/question/24304697
Keisha purchased a prepaid phone card for 25. Long distance calls cost 6 cents a minute using this card. Keisha used her card only once to make a long distance call. If the remaining credit on her card is 23.56 , how many minutes did her call last?
Answers
The prepaid card has an initial credit of $25
For long-distance calls, the cost is $0.06/min
After making a long-distance call the remaining credit is $23.56
To calculate the remaining credit you have to subtract the cost of the long-distance call to the initial credit on the card.
Let "x" represent the number of minutes the call lasted, then we can express the remaining credit on the card using the following expression:
\(23.56=25-0.06x\)From this expression, we can calculate the number of minutes (x) that the call lasted.
First, pass "25" to the left side of the expression by applying the opposite operation to both sides of it, i.e. subtract 25
\(\begin{gathered} 23.56-25=25-25-0.06x \\ -1.44=-0.06x \end{gathered}\)Second, divide both sides of the equation by -0.06 to determine the value of x:
\(\begin{gathered} -\frac{1.44}{-0.06}=-\frac{0.06x}{-0.06} \\ 24=x \end{gathered}\)x= 24 → this indicates that the call lasted 24 minutes.
Given g(x)=−x−1, find g(-4)
Answers
Answer:
3
Step-by-step explanation:
We just plug in -4 for x to get the equation: -(-4)-1. Negatives cancel out and we get 4-1 which is 3
Answer:
g(-4) = 3
Step-by-step explanation:
Plug in -4 for x in the given equation:
g(x) = - x - 1
g(-4) = - (-4) - 1
Note that if there are two negative signs directly next to each other, it would become a positive. Therefore:
- (-4) = 4
Simplify:
4 - 1 = 3
g(-4) = 3 is your answer.
~
Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature is 60 degrees at midnight and the high and low temperature during the day are 80 and 40 degrees, respectively. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.I don’t understand how my answer is wrong
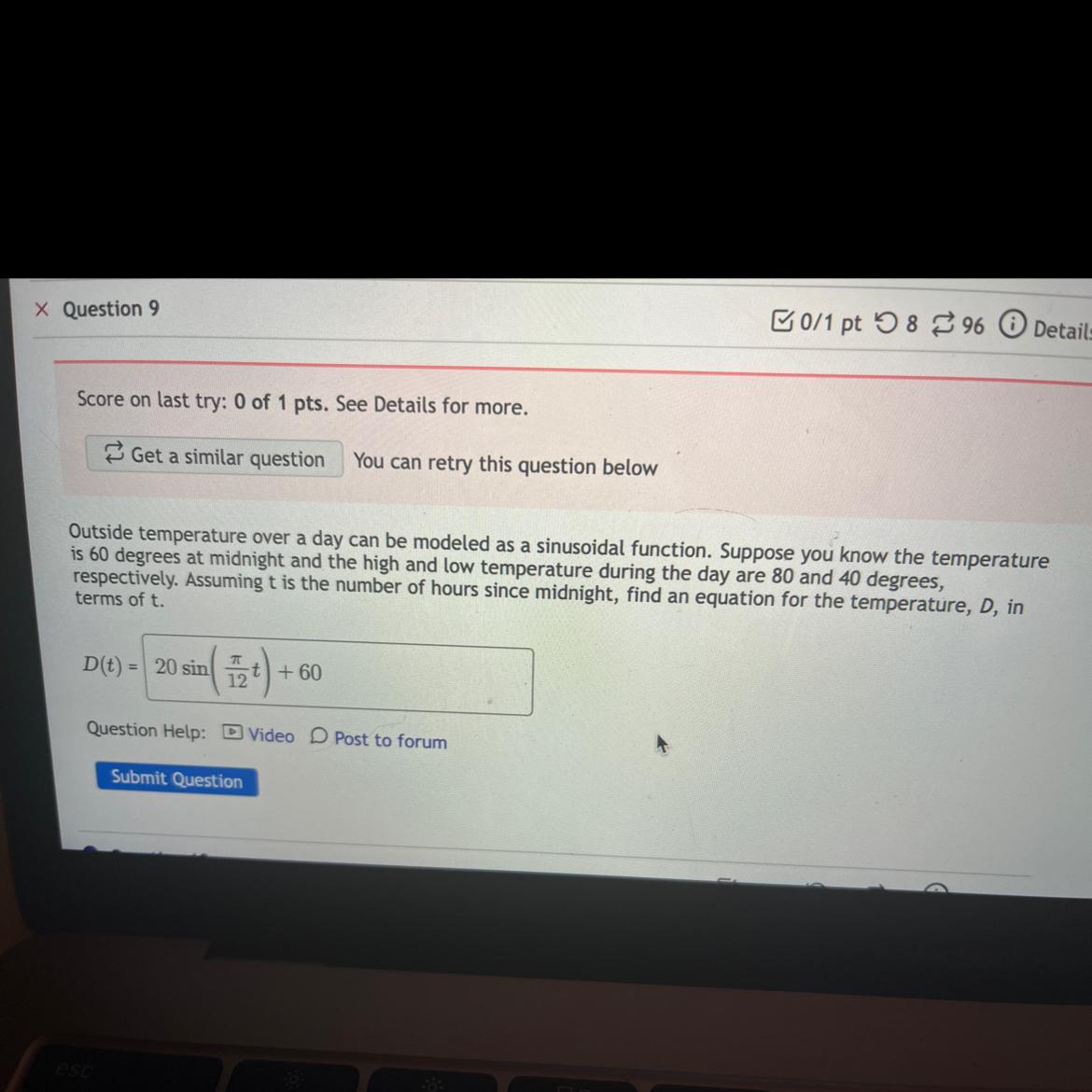
Answers
The range of the sin graph is the difference between the maximum and the minimum temperatures.
range = 80-40
amplituted = range/2 = 20
We also know that the period is 24 hours:
\(\begin{gathered} \frac{2\pi}{k\text{ }}\text{ = 24} \\ k\text{ = }\frac{\pi}{12} \end{gathered}\)When t = 0, temperature = 60
But we are told that the temperature does decrease after midnight so we need to flip the function vertically to make sure that it is still set to decrease and reach a minimum after midnight.
\(D(t)\text{ = -20sin\lparen}\frac{\pi}{12}t)\text{ + 60}\)2) 11 ft K-7 ft-K-8 ft- ·20 ft.
Answers
The area of the given figure is 192.5 ft².
Given is a figure we need to find its area,
By splitting the shape in 2, we can find the area.
Starting with the parallelogram (on the left), the area formula is A = b × h.
b (base) = 11 ft.
h (height) = 7 ft.
A (area) = (11 ft.)(7 ft.)
A = 77 ft.²
Then, the trapezoid's (on the right) area formula is A = [(a + b) ÷ 2] × h.
a (first base) = 8 ft.
b (second base) = (20 - 7) = 13 ft.
h (height) = 11 ft.
A = [(8 ft. + 13 ft.) ÷ 2] × 11 ft.
A = [(21 ft.) ÷ 2] × 11 ft.
A = (10.5 ft.) × 11 ft.
A = 115.5 ft.²
we can add them together to find the total area:
A = 77 ft.² + 115.5 ft.²
A = 192.5 ft.²
Hence, the area of the given figure is 192.5 ft².
Learn more about area click;
https://brainly.com/question/27683633
#SPJ1

find the perimeter of the composite figure. 11 19.5 16 m 18m

Answers
The perimeter of the composite figure that is given above would be = 96.6m.
How to calculate the perimeter of the given figure?To calculate the perimeter of the given shape, it has to be divided into two.
First shape is a rectangle. Therefore the perimeter of a rectangle is calculated with the formula = 2(l+w)
Where ;
length = 16m
width = 11m
perimeter = 2(16+11)
= 2×27
= 54m
The second shape:
Perimeter of triangle = l+w+h
where;
length = 18-11 = 7m
width = 16m
height = 19.5m
perimeter = 7+16+19.5 = 42.5m
Therefore, the perimeter of the shape = 54+42.5 = 96.6m
Learn more about perimeter here:
https://brainly.com/question/31619854
#SPJ1
Quinn bought a bouquet of flowers as a surprise for her grandfather. She had expected it would cost $15 but her prediction was 50% more than the actual cost of the flowers. What was the actual cost of the flowers?
Answers
To find 50% of 15, you multiply. 15*50% equals 7.5.
please help it's due tomorrow

Answers
Answer:
B. -414,720 x⁷y⁶
Step-by-step explanation:
To find the 4th term of the expansion of (2x - 3y²)¹⁰, we can use the binomial theorem.
The binomial theorem states that for an expression of the form (a + b)ⁿ:
\(\displaystyle (a+b)^n=\binom{n}{0}a^{n-0}b^0+\binom{n}{1}a^{n-1}b^1+...+\binom{n}{r}a^{n-r}b^r+...+\binom{n}{n}a^{n-n}b^n\\\\\\\textsf{where }\displaystyle \rm \binom{n}{r} \: = \:^{n}C_{r} = \frac{n!}{r!(n-r)!}\)
For the expression (2x - 3y²)¹⁰:
a = 2xb = -3y²n = 10Therefore, each term in the expression can be calculated using:
\(\displaystyle \boxed{\binom{n}{r}(2x)^{10-r}(-3y^2)^r}\quad \textsf{where $r = 0$ is the first term.}\)
The 4th term is when r = 3. Therefore:
\(\begin{aligned}\displaystyle &\;\;\;\;\:\binom{10}{3}(2x)^{10-3}(-3y^2)^3\\\\&=\frac{10!}{3!(10-3)!}(2x)^7(-3y^2)^3\\\\&=\frac{10!}{3!\:7!}\cdot2^7x^7(-3)^3y^6\\\\&=120\cdot 128x^7 \cdot (-27)y^6\\\\&=-414720\:x^7y^6\\\\ \end{aligned}\)
So the 4th term of the given expansion is:
\(\boxed{-414720\:x^7y^6}\)
PLZ HELP PLZZZZZZZZZ

Answers
Answer:
c.
Step-by-step explanation:
Rectangle JKLM is reflected across the x-axis and then the y-axis. The point I was
located at (-7, -3). What are the coordinates of point L after the two reflections?
Answers
Reflection involves mirroring a point over a line.
When L is reflected across the x and y axes, the new coordinates are (7,3)
Given that:
\((x,y) \to (-7,-3)\)
When a point is reflected across the x-axis, the rule is:
\((x,y) \to (x,-y)\)
So, we have:
\((-7,-3) \to (-7,3)\)
When a point is reflected across the y-axis, the rule is:
\((x,y) \to (-x,y)\)
So, we have:
\((-7,3) \to (7,3)\)
Hence, the new coordinates of L are (7,3)
Read more about reflections at:
https://brainly.com/question/17983440
5. Jermaine is thinking about attending college. However, he knows he
could get a job right out of high school making about $18,000 a year.
He could also work part time while attending 4 years of college and
make $7,000 a year. Assuming grants will pay for his college, how
long will it take Jermaine to recover his lost wages by choosing to go
to college instead of working full time after high school? He will make
$40,000 a year with his degree.
Answers
Answer:
2.5 years
Step-by-step explanation:
A teacher is 5 feet 8 inches tall and she shrinks to 9 inches. How tall will her pencil be if it undergoes the same scale shrink and was originally 12 inches?
A) 1.59 inches
B) 1.86 inches
C) 2.68 inches
D) 6.8 inches
Answers
Answer:
c
Step-by-step explanation:
2.68
A solid gold ingot has a volume of 200 cm3 and a mass of 3.9 kg.
What is the density of gold?
Answers
Step-by-step explanation:
convert 3.9 kg to grams
3.9×1000=3900 g
density = mass/ volume
= 3900/ 200
=19.5 g/cm3
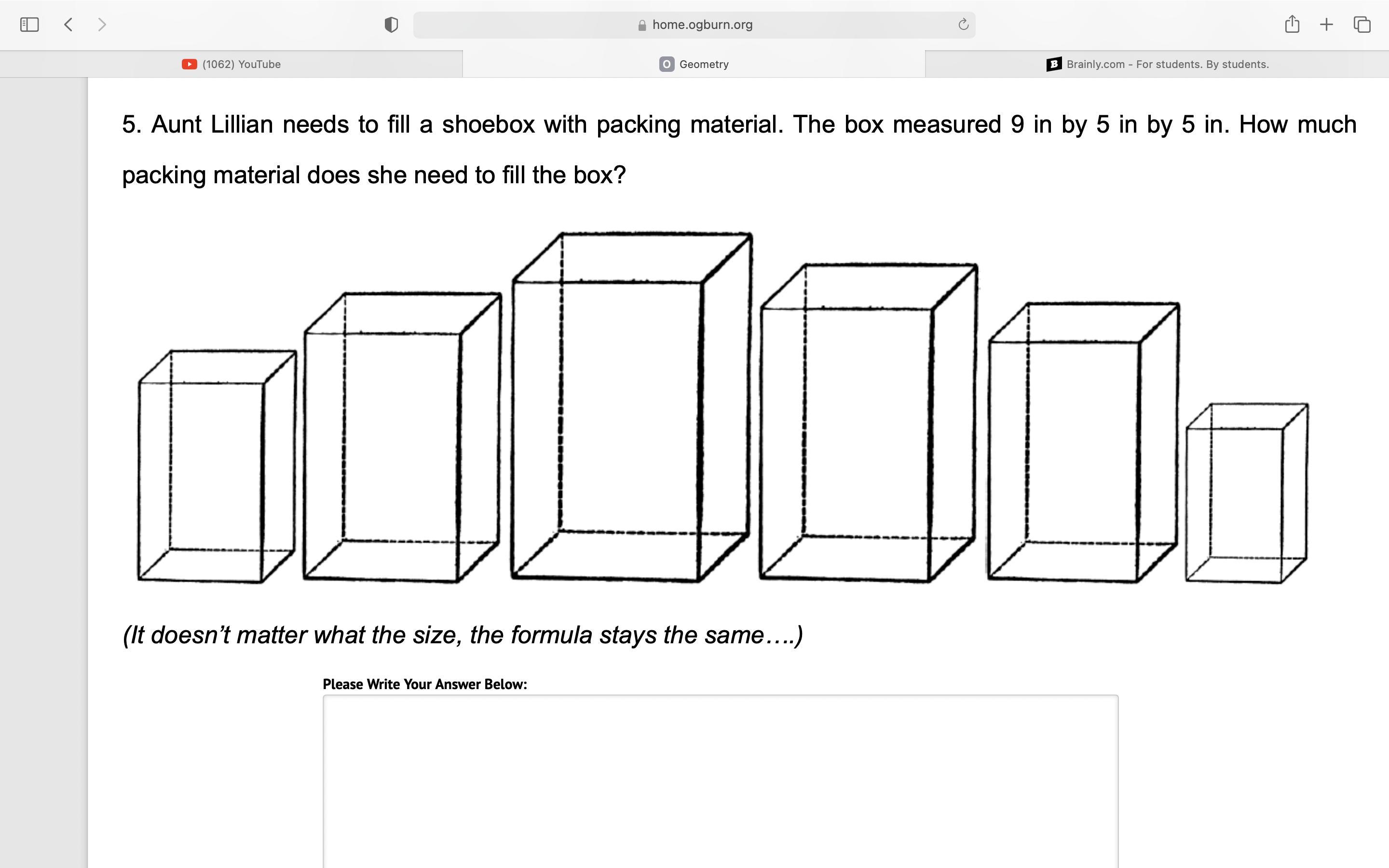
✎ READ AND ANSWER EACH PROBLEM
PLSS ANSWER IT THE QUESTION IS IN THE PICTURE ⬆︎⬆︎⬆︎⬆︎⬆︎

Answers
Answer:
2. 40
3. 10,500
4. 240
Step-by-step explanation:
The formula for volume is Length * Width * Height.
2. 5*2*4 = 40
3. 35*15*20= 10,500
4. 6*4*10=240
What percentage of the shape is blue?
Write your answer using a percent sign (%).

Answers
Answer:43%
Step-by-step explanation:
0.38, 1.52)
3
4
Over which interval does the growth rate of the exponential function continue to exceed the growth rate of the linear
function?
x = 0 to x= 3
x = 0 to x= 1.79
x=0.38 to x = 1.79
x= 1.79 to x - 3
Mark this and return
Save and Exit
Next
Submit
e here to search
Answers
Answer:
The best correct option is C
x = 1.79 to x = 3
Step-by-step explanation:
Making the sport off all little thing that crowed. They are still grouped into 7. Option C is theost appropriate.
Answer:
An exponential function and a linear function are graphed below
Over which interval does the growth rate of the exponential function continue to exceed the growth rate of the linear function?
a) x=0 to x=3
b) x=0 to x=1.79
c) x=0.38 to x= 1.79
d) x= 1.79 to x=3 <<<<<<< correct answer
Step-by-step explanation:
EDGE 2021
You are given that z > 2. Write an inequality for each expression.
a) 2z+ 9
b) 3(z - 4)
c) 4+2z
d) 5(3z-2)
Answers
a) The inequality for the expression 2z + 9 is 2z + 9 > 13.
b) The inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The inequality for the expression 4 + 2z is 4 + 2z > 8.
d) The inequality for the expression 5(3z - 2) is 15z - 10 > 20.
a) To write an inequality for the expression 2z + 9, we can multiply the given inequality z > 2 by 2 and then add 9 to both sides of the inequality:
2z > 2 * 2
2z > 4
Adding 9 to both sides:
2z + 9 > 4 + 9
2z + 9 > 13
Therefore, the inequality for the expression 2z + 9 is 2z + 9 > 13.
b) For the expression 3(z - 4), we can distribute the 3 inside the parentheses:
3z - 3 * 4
3z - 12
Since we are given that z > 2, we can substitute z > 2 into the expression:
3z - 12 > 3 * 2 - 12
3z - 12 > 6 - 12
3z - 12 > -6
Therefore, the inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The expression 4 + 2z does not change with the given inequality z > 2. We can simply rewrite the expression:
4 + 2z > 4 + 2 * 2
4 + 2z > 4 + 4
4 + 2z > 8
Therefore, the inequality for the expression 4 + 2z is 4 + 2z > 8.
d) Similar to the previous expressions, we can distribute the 5 in the expression 5(3z - 2):
5 * 3z - 5 * 2
15z - 10
Considering the given inequality z > 2, we can substitute z > 2 into the expression:
15z - 10 > 15 * 2 - 10
15z - 10 > 30 - 10
15z - 10 > 20
Therefore, the inequality for the expression 5(3z - 2) is 15z - 10 > 20.
for such more question on inequality
https://brainly.com/question/17448505
#SPJ8
Write an equation that could represent this situation: A builder needs to build a stack of bricks and take a break when the stack is 9 1/2 feet tall. He has built 1/3 of the stack already. How tall will the stack be when it is completed?
Answers
Answer:
273/6 feet is tall when work is complete
Given ∠A and ∠B are vertical angles with m∠A=20x+10 and m∠B=30x−10 .
What is x?
Enter your answer in the box.
ILL GIVE BRAINLIEST THANK YOU
Answers
Answer:
since angle a and b are vertical angles
therefore we can say that,
i) <A=<B
or,20x+10=30x-10
or,10+10=30x-20x
or,20=10x
.°. x=10.
Answer:
9
Step-by-step explanation:
Let the vector v have an initial point at (1,−1) and a terminal point at (7,2) what is the direction angle?
Answers
The direction angle of the vector with initial point (1, -1) and terminal point (7, 2) is approximately 26.57 degrees, found by calculating the arctangent of the ratio of the y and x components of the vector.
The direction angle of the vector v is the angle it makes with the positive x-axis, measured counterclockwise.
To find this angle, we need to calculate the difference between the y-coordinates and x-coordinates of the terminal and initial points of the vector, respectively. Then, we can use the arctangent function to find the angle.
Let's first find the components of the vector v
v = <7 - 1, 2 - (-1)> = <6, 3>
Now, we can find the direction angle as follows
θ = arctan(3/6)
θ = 0.4636 radians (in decimal form)
To convert this to degrees, we can multiply by 180/π
θ ≈ 26.57°
Therefore, the direction angle of the vector v is approximately 26.57 degrees.
To know more about direction angle:
https://brainly.com/question/28522105
#SPJ1
A young sumo wrestler decided to go on a special diet to gain weight rapidly. He gained weight at a constant rate.
The table compares the wrestler's weight (in kilograms) and the time since he started his diet (in months).
Time (months) Weight (kilograms)
1.5
1.51, point, 5
85.8
85.885, point, 8
3.0
3.03, point, 0
93.6
93.693, point, 6
4.5
4.54, point, 5
101.4
101.4101, point, 4
What was the wrestler's weight before he went on his diet?
Answers
The wrestler's weight before he went on his diet was 78.0 kilograms.
What is y-intercept?
In the context of a graph of a function, the y-intercept is the point where the graph intersects the y-axis. It is the value of the dependent variable (y) when the independent variable (x) is zero. Geometrically, the y-intercept is the value of the function at the point where it crosses the y-axis.
To determine the wrestler's weight before he went on his diet, we need to find the y-intercept of the linear function that represents his weight gain over time. This is because the y-intercept corresponds to the initial weight of the wrestler, i.e., his weight before he started his diet.
We can use the two data points where the time is 0 (i.e., at the start of the diet) to find the slope of the linear function:
(1.5, 85.8) and (3.0, 93.6)
The change in weight over the time interval of 1.5 to 3.0 months is:
93.6 - 85.8 = 7.8
The change in time over that interval is:
3.0 - 1.5 = 1.5
So the slope of the linear function is:
7.8 / 1.5 = 5.2
Now we can use the point-slope form of a linear function to write an equation for the wrestler's weight gain over time:
y - 85.8 = 5.2(x - 1.5)
where y represents the wrestler's weight and x represents the time in months.
To find the wrestler's weight before he went on his diet, we need to evaluate this equation at x = 0:
y - 85.8 = 5.2(0 - 1.5)
y - 85.8 = -7.8
y = 78.0
Therefore, the wrestler's weight before he went on his diet was 78.0 kilograms.
To learn more about y-intercept, visit the link:
https://brainly.com/question/29501432
#SPJ9
Amy wants to her ice cream cone filled exactly to the top. The radius of the cone is 2 in. and the height is 6 in. How much ice cream will it take to fill the cone?


Answers
Answer:
Answer given below in the following pictures.
I hope my answer helps you.

The sale price of a swimming pool after a 18.5% discount is $1092.10. Find the original list price of the pool.
Answers
.835x=1210.75 but where did i get .835 from?
.835 .835
X=1450
What is the solution to the system of equations below? x + 3 y = 15 and 4 x + 2 y = 30 (4, 10) (3, 6) (6, 3) (10, 4)
Answers
Answer:
x=15-3yin second equation,
4x+2y=30
2(2x+y)=30
2x+y=15
Now,putting the value of x from above
2×(15-3y)+y=15
30-6y+y=15
30-15=5y
y=3
Then,
x=15-3×3
x=6
#(6,3) is ans
Answer:
(6,3)
Step-by-step explanation: