Answers
Step-by-step explanation:
Pick ANY point in the blue region
(2,2) would be one of infinite possibilities
Related Questions
. Зn – 1 = 8
Pls tell me what n equals lol
Answers
Answer:
Зn – 1 = 8
3n=9
n=3
Hope This Helps!!!
Answer:
n=3
Step-by-step explanation:
add 1 to both sides
then divide both sides by 3
A project has five activities with the durations (days) listed
below:
Activity
Precedes
Expected
Duration
Variance
Start
A, B
-
-
A
C
40
0.31
B
E
32
0.25
C
D
21
0.35
Answers
The critical path is the path with the longest duration, which in this case is A -> B -> D -> E with a duration of 11 days.
To determine the critical path of the project, we need to find the longest path of activities that must be completed in order to finish the project on time. This is done by calculating the earliest start time (ES) and earliest finish time (EF) for each activity.
Starting with activity A, ES = 0 and EF = 4. Activity B can start immediately after A is complete, so ES = 4 and EF = 7. Activity C can start after A is complete, so ES = 4 and EF = 6. Activity D can start after B is complete, so ES = 7 and EF = 9. Finally, activity E can start after C and D are complete, so ES = 9 and EF = 11.
The variance for each activity is also given, which allows us to calculate the standard deviation and determine the probability of completing the project on time. The critical path is the path with the longest duration, which in this case is A -> B -> D -> E with a duration of 11 days.
Using the expected durations and variances, we can calculate the standard deviation of the critical path. This information can be used to determine the probability of completing the project on time.
Know more about earliest start time here:
https://brainly.com/question/31043653
#SPJ11
what is it the answer to 1/4 =100
Answers
The answer for the fraction 1/4 of 100 is 25.
Given,
The fraction; 1/4
We have to find the 1/4 of 100.
Fraction;
A fraction is referred to as the portion of a whole in mathematics. For instance, if a pizza is cut into four equal pieces, each one is represented by a quarter. Fractions make calculations quicker and easier by making it easier to distribute and judge numbers.
There are three main categories of fractions in mathematics. Proper fractions, incorrect fractions, and mixed fractions are these three types. The expressions with a numerator and a denominator are called fractions
Here,
1/4 of 100 = 1/4 x 100 = 25.
That is,
The answer for the fraction 1/4 of 100 is 25.
Learn more about fractions here;
https://brainly.com/question/17058737
#SPJ1
For number 8 find the variable using the properties of a parallelogram

Answers
Applying one of the properties of a parallelogram, the value of x is 10°, then 6x=60° and 12x=120°.
QuadrilateralsThere are different quadrilaterals, for example square, rectangle, rhombus, trapezoid, and parallelogram. Each type is defined accordingly to its length of sides and angles. For example, a parallelogram presents some properties that are presented below.
the opposite sides are equal and parallelthe opposite angles and the diagonals are equal.the adjacent angles are supplementary.The figure of the exercise shows two adjacent angles. From the property: the adjacent angles are supplementary, you have:
6x+12x=180
18x=180
x=10°
Therefore, 6x= 6*10=60° and 12x=12*10=120°.
Read more about the parallelogram here:
brainly.com/question/20526916
#SPJ1
Johnny charges $10 plus $7.50 per hour to mow lawns.
Answers
The linear equation of Johnny's charges is C(x) = 10 + 7.5x
How to determine the linear equationFrom the question, we have the following parameters that can be used in our computation:
Initial charge = $10
Hourly rate = $7.50
Let the number of hours be x and the total cost be C(x)
So, we have the following representation
C(x) = Initial charge + Hourly rate * x
Substitute the known values in the above equation, so, we have the following representation
C(x) = 10 + 7.5x
Hence, the function is C(x) = 10 + 7.5x
Read more about linear function at
https://brainly.com/question/15602982
#SPJ1
Complete question
Johnny charges $10 plus $7.50 per hour to mow lawns.
Determine the linear equation
In the parallelogram find the values of x and y

Answers
x+4=12 (parallel)
x= 12-4=8
I need help
how do I do this?

Answers
Answer:
lol easy its 5
Step-by-step explanation:
Find the equations of the tangents to the curve x = 6t^2 + 4, y = 4t^3 + 4 that pass through the point (10, 8). y=?? (smaller slope)
y=?? (larger slope)
Answers
The equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Curve isx = 6t^2 + 4, y = 4t^3 + 4the slope of tangent of this curve dy/dx is dy/dx=12t/(3t^2+2)Then, equation of tangent with slope m and passing through (x1, y1) is given by(y - y1) = m(x - x1) ............(1)Here, point is (10,8)Therefore, equation of tangent passing through (10, 8) will be of the form(y - 8) = m(x - 10)Let this tangent intersect the curve at point P. Then, the coordinates of point P are given byx = 6t^2 + 4y = 4t^3 + 4.
Equating this with equation (1), we get:4t^3 + 4 - 8 = m(6t^2 - 6)4t^3 = 6m(t^2 - 1)2t^3 = 3m(t^2 - 1)2t^3 + 3mt - 3m = 0t = -m/2 ± sqrt(m^2/4 + 3m)Therefore, the two tangents are given by:y - 8 = m1(x - 10), where m1 = -3/2 + sqrt(37)/2y - 8 = m2(x - 10), where m2 = -3/2 - sqrt(37)/2Hence, the equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Learn more about slope tangent here:
https://brainly.com/question/32393818
#SPJ11
Find the degree of the monomial.
6r2n4t

Answers
Answer:
idek
Step-by-step explanation:
Please Help!
Which inequality does this graph show?

Answers
Answer: Y= -5x+4
Step-by-step explanation:
Use <, >, or to compare the following numbers.
-12
8
9
0
-10
1
Answers
Answer:
-12 < 8 < 9 > 0 > -10 < 1
HELP ASPA PLEASE I will give brainliest
A state uses a combination of three letters (A – Z) followed by three digits (0 – 9) for
their standard vehicle license plates. How many different standard license plates are
possible using a combination of three letters followed by three digits.
Answers
Answer:
2340
Step-by-step explanation:
fundamental counting principle
Select all the equations where x = 3 is a solution.
Choose 2 answers:
А )x +4= 7
B) = 3 9 5 - 2 = 2
D) 8x = 32
E )X – 10 = 7
Answers
Answer:
Step-by-step explanation:
X +4=
8x=32
If O is an optimal solution to a linear program, then O is a
vertex of the feasible region. How do you prove
this?
Answers
To prove that if O is an optimal solution to a linear program, then O is a vertex of the feasible region, we can use the following argument:
Assume that O is an optimal solution to a linear program.
By definition, an optimal solution maximizes or minimizes the objective function while satisfying all the constraints.
Suppose O is not a vertex of the feasible region.
If O is not a vertex, it must lie on an edge or in the interior of a line segment connecting two vertices.
Consider two neighboring feasible solutions, A and B, that define the line segment containing O.
Since O is not a vertex, there exists a feasible solution on the line segment between A and B that has a higher objective function value (if maximizing) or a lower objective function value (if minimizing) than O.
This contradicts our assumption that O is an optimal solution since there exists a feasible solution with a better objective function value.
Therefore, our initial assumption that O is not a vertex must be false.
Thus, O must be a vertex of the feasible region.
By contradiction, we have shown that if O is an optimal solution to a linear program, then O must be a vertex of the feasible region.
me pueden mandar un ejercicio de polinomios que incluyan suma resta y multiplicacion resueltos y otra que incluya suma multiplicación y división. SE GANARAN 25 PUNTOS!!!!!!!
Answers
Answer:
?que significa POLINOMIOS?
Answer:
Step-by-step explanation:
Come up with two examples of ratio relationships that are interesting to you.
Answers
Answer:
radio relationships?what do u mean?
Find the slope of each line. Tell whether the slop is Positive, Negative, Undefined or Zero

Answers
Because the line crosses at the y axis and you would have to find another line that’s right on the corner of a square, so you divide 1 and 1 and it’s 1
Find the quotient: which expression is the result of dividing?
y - 2 underroot 3y^2 + 2y + 7
a. 3y – 4 –
b. 3y + 8 +
c. 3y + 8 –
d. 3y – 4 +
Answers
Answer:
你好你妈妈
Step-by-step explanation:
on a circle of radius 2, center (0, 0), find the x and y coordinates at angle 270 degrees (or 3π/2 in radian measure).
Answers
At an angle of 270 degrees (or 3π/2 radians) on a circle with a radius of 2 and center at (0, 0), the x-coordinate is 0 and the y-coordinate is -2.
To find the x and y coordinates at an angle of 270 degrees (or 3π/2 in radian measure) on a circle of radius 2 with center (0, 0), we can use the trigonometric definitions of sine and cosine.
The x-coordinate (x-value) represents the horizontal position on the circle, while the y-coordinate (y-value) represents the vertical position.
For a point on the unit circle (circle with radius 1) at a given angle θ, the x-coordinate is given by cos(θ) and the y-coordinate is given by sin(θ).
In this case, the circle has a radius of 2, so we need to multiply the cosine and sine values by 2 to get the x and y coordinates, respectively.
Using the angle 270 degrees (or 3π/2 in radian measure):
x-coordinate = 2 * cos(3π/2)
y-coordinate = 2 * sin(3π/2)
Evaluating these expressions:
x-coordinate = 2 * cos(3π/2) = 2 * 0 = 0
y-coordinate = 2 * sin(3π/2) = 2 * (-1) = -2
Therefore, at an angle of 270 degrees (or 3π/2 radians) on the circle of radius 2 with center (0, 0), the x-coordinate is 0 and the y-coordinate is -2.
To learn more about circles visit : https://brainly.com/question/24375372
#SPJ11
Find values of a and b that make the following equality into identity:
2x+5/(x-8)(2x+1)=a/x-8 + b/2x+1 !!!
please help!! giving 50 points
Answers
The value of a on that expression is 2\(\frac{1}{3}\) or 2,33. The value of b on that expression is 2\(\frac{2}{3}\) or 2,67.
How to find the value a and b?the first step you have to do is to simplify the expression as follow:
\(\frac{2x+5}{(x-8)(2x+1)} = \frac{a}{x-8} + \frac{b}{2x+1}\) .
\(\frac{2x+5}{(x-8)(2x+1)} = \frac{a(2x+1)}{(x-8)(2x+1)} + \frac{b(x-8)}{(2x+1)(x-8)}\)
\(\frac{2x+5}{(x-8)(2x+1)} = \frac{a(2x+1)+b(x-8)}{(x-8)(2x+1)}\)
2x + 5 = a(2x+1) + b(x-8)
2x + 5 = 2ax + a + bx - 8b
2x + 5 = (2a+b)x + (a - b)
Based on constant x, we can find out that:
2 = 2a+b
5 = a - b
Eliminate b, then
2 + 5 = 2a + a + b + (-b)
7 = 3a
a = 2\(\frac{1}{3}\) = 2.33
After getting a value then substitute a to 5 = a - b or 2 = 2a + b, then
5 = a - b
5 = 2\(\frac{1}{3}\) - b
b = 2\(\frac{1}{3}\) - 5
b = - 2\(\frac{2}{3}\) = -2.67
Learn more about math elimination here
https://brainly.com/question/14024488
#SPJ4
Jahari is making hamburgers for eight party guests. When Jahari weighs all of the hamburger meat, it weighs 5 pounds 8 ounces. Jahari wants to make hamburger patties that all weigh the same amount. About how many ounces does each hamburger patty weigh?
Answers
Answer:
11 ounces for each hamburger patty
Step-by-step explanation:
1 pound(lbs) = 16 ounces(oz)
Convert 5lbs into ounces
5x16 = 80oz
80 + 8 = 88 Add all the ounces together
/8 = Divide by 8 people
11oz each
Vector u has initial point at (4, 4) and terminal point at (–12, 8). Which are the magnitude and direction of u?
||u|| = 14.422; θ = 33.690°
||u|| = 14.422; θ = 146.310°
||u|| = 16.492; θ = 14.036°
||u|| = 16.492; θ = 165.964°
Answers
Let's find the magnitude of each component:
Let:
\((x1,y1)=(4,4)\)
\((x2,y2)=(-12,8)\)
\(u=ax+by\)
\(||u||=\sqrt{a^2+b^2}\)
So, let's find a and b:
\(a=|x2-x1|=|-12-4|=|-16|=16\)
\(b=|y2-y1|=|8-4|=|4|=4\)
so:
\(||u||=\sqrt{16^2+4^2}\)
\(||u||=\sqrt{272}\)
\(||u||\thickapprox16.492\)
And the direction is:
\(\theta=180-\text{tan}^{-1}\huge \text(\dfrac{b}{a}\huge \text)\)
\(\theta=180-\text{tan}^{-1}\huge \text(\dfrac{4}{16}\huge \text)\)
\(\theta\thickapprox180-\text{tan}^{-1}\huge \text(\dfrac{4}{16}\huge \text)\thickapprox165.964\)
The marketing club school is openings student store. They randomly survey 50 students who how much money they spend
onunch each day. What is the expected value for a student to spend on lunch each day?
Student Lunch Survey
Number of Dollars spent on
Students
Lunch Eschwy
510
SSS
05.18
5.07
See
signou
us
247
Answers
The expected value for a student to spend on lunch each day from the survey of 50 students is $5.18.
The expected value for a student to spend on lunch each day is derived from the survey of 50 students. This value is calculated by taking the total number of dollars spent by all of the surveyed students and dividing it by the total number of students surveyed. In this particular survey, the total number of dollars spent was $247, and the total number of students surveyed was 50. Dividing $247 by 50 gives us a value of $4.94. This value is then rounded up to the nearest cent to give us the expected value of $5.18. This expected value is the average amount of money that a student can expect to spend on lunch each day from the survey. It is important to note that this value is an estimate, as individual student spending habits may vary greatly.
Learn more about expected value here
https://brainly.com/question/18523098
#SPJ4
Find the equation of the line shown.
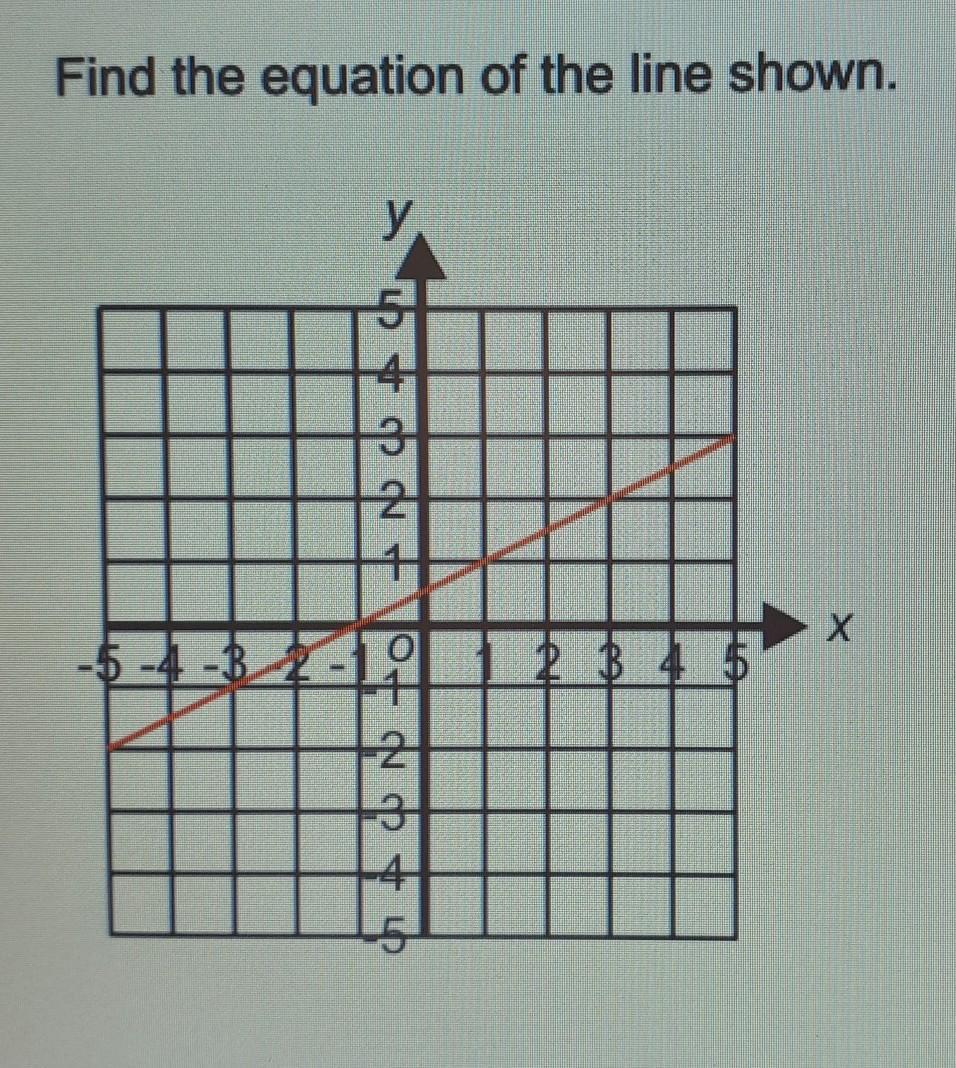
Answers
need desperate help, giving 100 pts

Answers
Answer:
(If you like this answer i would appreciate if u give brainliest but otherwise, i hope this helped ^^)
Step-by-step explanation:
Expanding the given expressions:
1. (3x+2)(4x-5) = 12x^2 - 15x + 8x - 10 = 12x^2 - 7x - 10
2. (5x-2)(2x+7) = 10x^2 + 35x - 4x - 14 = 10x^2 + 31x - 14
3. (x-4)(3x-y+3) = 3x^2 - xy + 3x - 12x + 4y - 12 = 3x^2 - xy - 9x + 4y - 12
4. (2y-1)(2y+1)(4y^2 +1) = (4y^2 - 1)(4y^2 + 1) = 16y^4 - 1
5. (3x-3)(8x+1) = 24x^2 + 3x - 24x - 3 = 24x^2 - 21x - 3
6. (-m-3)(2m-4) = -2m^2 + 4m + 6m - 12 = -2m^2 + 10m - 12
7. (5d-12)(3d+1) = 15d^2 + 5d - 36d - 12 = 15d^2 - 31d - 12
8. (3x^2+2x)(4x-1) = 12x^3 - 3x^2 + 8x^2 - 2x = 12x^3 + 5x^2 - 2x
9. (3t-13)(2t+2) = 6t^2 + 6t - 26t - 26 = 6t^2 - 20t - 26
10. (4a-2b)(12a+6b) = 48a^2 + 24ab - 24ab - 12b^2 = 48a^2 - 12b^2
19. Solve the following equations for x where x E [0, 2π]. a. sin(x) = - = c. 4 sin²(x) - 2 = 0 e. tan(x) = 1 b. cos(x) = -√2 d. sec(x) = 2 f. sin(2x) =
Answers
The interval [0, 2π], the solutions to this equation are x = 0, x = π/2, x = π, and x = 3π/2. These angles correspond to points on the unit circle where the y-coordinate is zero.
a. **Solving sin(x) = -1** in the interval [0, 2π]:
The equation sin(x) = -1 represents the value of the sine function equal to -1. In the given interval [0, 2π], the solutions to this equation are x = 3π/2 and x = 7π/2.
To understand this, we can visualize the unit circle. The sine function is negative at the angles 3π/2 and 7π/2, which correspond to the points (-1, 0) and (-1, 0) on the unit circle, respectively.
b. **Solving cos(x) = -√2** in the interval [0, 2π]:
The equation cos(x) = -√2 indicates that the cosine function equals -√2. However, there are no real solutions for this equation in the given interval [0, 2π]. The range of the cosine function is [-1, 1], and there is no value within this range that equals -√2.
c. **Solving 4sin²(x) - 2 = 0** in the interval [0, 2π]:
To solve this equation, we can rearrange it as 4sin²(x) = 2, and then divide both sides by 4 to obtain sin²(x) = 1/2. Taking the square root of both sides, we have sin(x) = ±√(1/2).
In the interval [0, 2π], the solutions to sin(x) = √(1/2) are x = π/4 and x = 3π/4. Similarly, the solutions to sin(x) = -√(1/2) are x = 5π/4 and x = 7π/4.
d. **Solving sec(x) = 2** in the interval [0, 2π]:
The equation sec(x) = 2 represents the secant function equal to 2. To solve this equation, we can take the reciprocal of both sides, yielding cos(x) = 1/2.
Within the interval [0, 2π], the solutions to cos(x) = 1/2 are x = π/3 and x = 5π/3. These angles correspond to points on the unit circle where the x-coordinate is 1/2.
e. **Solving tan(x) = 1** in the interval [0, 2π]:
The equation tan(x) = 1 signifies that the tangent function equals 1. In the given interval, the solutions to this equation are x = π/4 and x = 5π/4. These angles correspond to points on the unit circle where the y-coordinate is equal to the x-coordinate.
f. **Solving sin(2x) = 0** in the interval [0, 2π]:
The equation sin(2x) = 0 indicates that the sine of twice the angle is equal to zero. This implies that 2x is an integer multiple of π.
Within the interval [0, 2π], the solutions to this equation are x = 0, x = π/2, x = π, and x = 3π/2. These angles correspond to points on the unit circle where the y-coordinate is zero.
Learn more about interval here
https://brainly.com/question/27896782
#SPJ11
Polynomial Regression: Method of Least Squares My Solutions Problem Description: Read Chapter 15, "General Linear Least-Squares and Nonlinear Regression," from Chapra's textbook and watch/review Lecture 11. Using the same approach as was employed to derive Eqs. (14.15) and (14.16), derive the least-squares fit of the following model: y = a1*x + a2*x^2 That Is, determine the coefficients that result in the least-squares fit for a second-order polynomlal with a zero Intercept.
Answers
To derive the least-squares fit for the model y = a1x + a2x^2 with a zero intercept, we need to minimize the sum of squared residuals. Let's denote the observed data points as (xi, yi) for i = 1 to n.
The objective is to find the values of a1 and a2 that minimize the following sum of squared residuals:
SSR = ∑(yi - (a1xi + a2xi^2))^2
To find the minimum, we differentiate SSR with respect to a1 and a2 separately and set the derivatives equal to zero.
Partial derivative with respect to a1:
∂SSR/∂a1 = -2∑(yi - (a1xi + a2xi^2))*xi = 0
Partial derivative with respect to a2:
∂SSR/∂a2 = -2∑(yi - (a1xi + a2xi^2))*xi^2 = 0
Expanding the above equations:
∑(yixi) - a1∑(xi^2) - a2∑(xi^3) = 0 ------ (1)
∑(yixi^2) - a1∑(xi^3) - a2∑(xi^4) = 0 ------ (2)
Now, let's solve these equations to find the values of a1 and a2.
From equation (1):
a1∑(xi^2) + a2∑(xi^3) = ∑(yi*xi) ------ (3)
From equation (2):
a1∑(xi^3) + a2∑(xi^4) = ∑(yi*xi^2) ------ (4)
We can express equations (3) and (4) in matrix form as:
| ∑(xi^2) ∑(xi^3) | | a1 | = | ∑(yixi) |
| ∑(xi^3) ∑(xi^4) | | a2 | = | ∑(yixi^2) |
Solving this system of linear equations will give us the values of a1 and a2.
Once a1 and a2 are determined, we have the least-squares fit of the model y = a1x + a2x^2 with a zero intercept.
Know more about least-squares here:
https://brainly.com/question/29834077
#SPJ11
If you reflect a point from quadrant IV over the x axis, where will the
new point be located. *
Answers
Answer:
Quadrant I
Step-by-step explanation:
Quadrant IV (bottom right corner) reflects over the x axis into the top right corner or Quadrant I
find every point cc in the interval [−2,0] at which f(x)=9x3 takes on its average value. separate multiple answers with a comma. write the exact answer. do not round.
Answers
Answer:
the exact answer is x = -∛2.
Step-by-step explanation:
The average value of a function over an interval [a, b] is given by:
Avg = (1 / (b - a)) * ∫[a to b] f(x) dx
In this case, the interval is [−2, 0], so a = -2 and b = 0.
Avg = (1 / (0 - (-2))) * ∫[-2 to 0] (9x^3) dx
= (1 / 2) * ∫[-2 to 0] (9x^3) dx
= (1 / 2) * [9/4 * x^4] | [-2 to 0]
= (1 / 2) * (9/4 * (0^4 - (-2)^4))
= (1 / 2) * (9/4 * (0 - 16))
= (1 / 2) * (9/4 * (-16))
= (1 / 2) * (-36)
= -18
The average value of f(x) = 9x^3 over the interval [-2, 0] is -18.
Now, we need to find the points in the interval where the function takes on this average value of -18.
Setting f(x) = -18, we have:
9x^3 = -18
Dividing both sides by 9:
x^3 = -2
Taking the cube root of both sides:
x = -∛2
Therefore, the point cc in the interval [-2, 0] where f(x) = 9x^3 takes on its average value of -18 is x = -∛2.
i hope i helped!
(Chapter 14) If f(x,y) has two local maximal, then f must have a local minimum.TrueFalse
Answers
It is true that the existence of two local maxima does not guarantee the presence of a local minimum. It is possible for a function to have multiple local maxima and no local minimum.
For example, consider the function f(x,y) = x^4 - 4x^2 + y^2. This function has two local maxima at (2,0) and (-2,0), but no local minimum. Therefore, the statement "if f(x,y) has two local maximal, then f must have a local minimum" is false. The presence or absence of local maxima and minima depends on the behavior of the function in the immediate vicinity of a point, and cannot be determined solely based on the number of local maxima. It is possible for a function to have an infinite number of local maxima and minima, or none at all. Therefore, it is important to carefully analyze the behavior of a function in order to determine the presence or absence of local extrema.
Know more about maxima here:
https://brainly.com/question/31387277
#SPJ11
