Answers
okay so the 2x+6 is the red line
x<12 is the purple region
-3/4x+8 is the blue line
x is greater than or equal to 12 is black
the second picture shows when 8 ≤ x ≤ 16
in the second photo it shows the region where 8≤x≤12 which is the red shaded part


Related Questions
Draw the polygon with the given vertices in a coordinate plane.
22).(-5,5),(-4,1) pls help
Answers
Plot the given coordinates of the polygon in the coordinate plane and connect it with a smooth curve.
What are polygons?A two-dimensional geometric shape with a finite number of sides is called a polygon. A polygon's sides are constructed from segments of straight lines joined end to end.
What is a coordinate plane?A coordinate plane is a two-dimensional plane created by the intersection of two number lines. The x-axis, a horizontal number line, and the y-axis, a vertical number line, are two of these number lines.
Plot the points on the graph according to the given coordinates. Connect all the points. The polygon is triangle.
Learn more about polygon here:
https://brainly.com/question/24464711
#SPJ1

Lol shoe very good shoe

Answers
I need help please I can only find 2 of these solutions

Answers
Step 1: Isolate the Sin Operator
\(8 sin(\frac{\pi }{6} x)=2\\sin(\frac{\pi }{6} x)=0.25\\\\\)
Step 2: Use Inverse Sin(arcsin) to isolate the term with the x variable
Note that since trig functions have 2 general solutions, this will give us one of our general solutions.
\(x=\frac{6 arcsin(0.25)}{\pi } =0.48\)
x₁= 0.48
Solving for x₂
Use the period identity for Sin Functions
\(sin(x)=sin(\pi -x)\)
X in this case is arcsin(0.25)
\(\frac{\pi }{6} x=\pi -arcsin(0.25) = 5.52\)
So our two general solutions are 0.48 and 5.52
Step 3: Period
Trig Functions have periodic behavior and this function period is
\(\frac{2\pi }{1} (\frac{6}{\pi } )= 12\)
So our general solutions are
0.48±12k, where k is an integer
5.52±12k, where k is an integer
Let k=1, and we get our next set of solutions:
12.48 and 17.52
So our answer is 0.48,5.52,12.48,17.52
ILL GIVE BRAINEST Simplify the expression.
3 + 8(2x - 1) - 2x
O A. -18x- 4
O B. 14x + 2
O C. 14x-5
D. -18x - 11
Answers
Answer:
c
Step-by-step explanation:
...................................
Evaluate 26 + a if a = 8
Answers
Answer:
34
Step-by-step explanation:
= 26 + 8
= 34
Complete the square to re-write the quadratic function in vertex form:
y= x2 - 5x +9
Answer: y =
Submit Answer
Answers

What is the surface area of the figure shown? (Use 3.14 for pi.)

Answers
I need help on this question
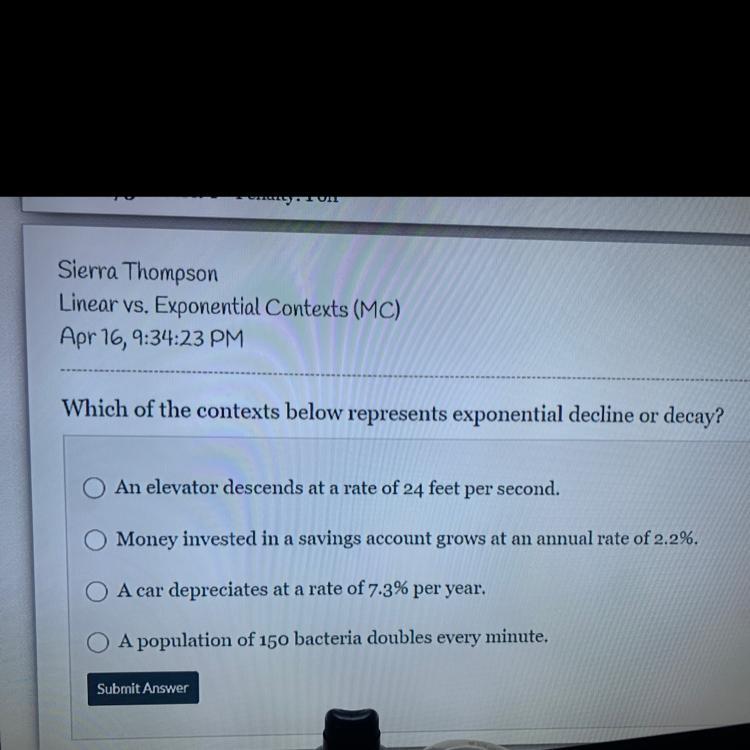
Answers
The correct option is the third one, it can be written as the equation:
y = A*(1 - 0.073)ˣ
Which one represents an exponential decay?A general exponential decay can be written as:
y = A*(b)ˣ
Where A is the initial value, and b is the base.
It is an exponential decay only if 0 < b < 1.
From the given options, the one that can be modeled with an exponential decay is a car whose price depreciuates at a rate of 7.3% per year, because if the initial price of the car is A, we can write it as:
y = A*(1 - 0.073)ˣ
Learn more about exponential decays at:
https://brainly.com/question/27822382
#SPJ1
Each side length of a triangle is 4 cm. What type of triangle is it?
☐ right
□acute
Equilateral
Isosceles
Answers
Answer: Equilateral
Step-by-step explanation:
It's equilateral because it says that each side of the triangle is 4cm. In simple words, all the sides of triangle are equal. Such a triangle is called an equilateral triangle.
Hope you understood.
please help meeeeee!!!!!!!!!!!!!

Answers
Answer:
\(\mbox{\large t = \boxed{1} second}\)
Step-by-step explanation:
The function relating time and height of the ball is given as
\(h(t) = -16t^2 + 16t + 320\cdots\cdots \cdots(1)\)
with the variables h, t as defined in the question
We are asked to find the time at which the ball reaches a height of 320 feet
Substitute 320 for h in Equation (1) and solve for t
\(320 = -16t^2 + 16t + 320\\\\\textrm{Switching sides, }\\\\\\-16t^2 + 16t + 320 = 320\\\\\textrm{Subtract 320 from both sides to get}\\\\\\-16t^2 + 16t = 0\)
Carry 16t to the right side:
\(-16t^2 = -16t\\\\\)
Divide both sides by -16t:
\(\dfrac{-16t^2}{-16t} = \dfrac{-16t}{-16t}\\\\\implies t = 1\)
That means the ball has a height of 320 feet when t = \(\boxed{1}\) second
We can check if this correct by plugging in t=1 into the original equation:
At t = 1
- 16t² + 16t + 320
= -16(1)² + 16(1) + 320
= -16 + 16 + 320
= 320
Hence t = 1 checks out
Answer: the ball has height 320 feet when t=0, 1 seconds
Step-by-step explanation:
\(Given: \ h(t)=-16t^2+16t+320\ \ \ \ h(t)=32\ feet\\\\Find\ t\geq 0\\\\\)
\(Solution\)
\(h(t)=-16t^2+16t+320\\\\320=-16t^2+16t+320\\\\0=-16t^2+16t\\\\0+16t^2=-16t^2+16t+16t^2\\\\16t^2=16t\\\\16t^2-16t=16t-16t\\\\16t^2-16t=0\\\\16(t^2-t)=0\)
We divide both parts of the equation by 16:
\(\displaystyle\\t^2-t=0\\\\t(t-1)=0\\\\\left \{ {{t=0} \atop {t-1=0}} \right. \ \ \ \ \ \ \Rightarrow\\\\t=0 \ \ \ \ t=1\)

the kappa iota sigma fraternity polled its members on the weekend party theme. the vote was as follows: six for toga, four for hayride, eight for beer bash, and two for masquerade. display the vote count in a pareto chart.
Answers
Pareto chart is a type of bar graph which often displays the data in descending order of frequency.
It is made up of vertical bars, with the height of each bar representing the frequency of occurrence for each category. The chart is named after Vilfredo Pareto, who used it to analyze economic data in the late 19th century.
For the given data, we calculate the cumulative frequency of the data by adding the frequencies of each category.
Toga: 6
Hayride: 6 + 4 = 10
Beer Bash: 10 + 8 = 18
Masquerade: 18 + 2 = 20
The Pareto chart is created by plotting the cumulative frequency against the categories. The chart is plotted with the categories on the x-axis and the cumulative frequency on the y-axis.
Toga: 6 (30%)
Hayride: 10 (50%)
Beer Bash: 18 (90%)
Masquerade: 20 (100%)
Hence, the Pareto chart for the given data is as follows:
Toga: 30%
Hayride: 20%
Beer Bash: 40%
Masquerade: 10%
Learn more about Pareto chart here:
https://brainly.com/question/17840218
#SPJ4
12 cupcakes cost $16.79 what is the unit price
Answers
Answer:
The unit price is $1.3991 or $1.40 when rounded
Step-by-step explanation:
To find the unit rate you divide the price by the amount of cupcakes. This would be set up as $16.79÷12
Find the measure of TU
A. 8
B. 12
C. 14
D. 11

Answers
Answer:
D. 11
Step-by-step explanation:
First apply the secant-secant theorem to find the value of x.
Thus,
VU(TU + VU) = VW(BW + VW) (secant-secant theorem)
Substitute
(7)(x + 4 + 7) = (9)(-2 + x + 9)
7(x + 11) = 9(7 + x)
7x + 77 = 63 + 9x
Collect like terms
7x - 9x = 63 - 77
-2x = -14
Divide both sides by -2
x = 7
✔️Find TU
TU = x + 4
Substitute get value of x
TU = 7 + 4 = 11
Answer:
11
Step-by-step explanation:
Given: A (-3, 5) and B (4, -2), what is the length of AB?
Answers
After considering the given data we come to the conclusion that the length of AB is 12.124 units, under the condition that A (-3, 5) and B (4, -2) are the given coordinates.
The distance between two points in a plane can be found using the distance formula which is an application of the Pythagorean theorem. The formula is given by d=√ ( ((x₂ – x₁ )² + (y₂ – y₁ )²)
Here (x₁, y₁) and (x₂, y₂) are the coordinates of the two points.
Applying the given coordinates of A (-3, 5) and B (4, -2), we can evaluate the distance between them as follows:
d = √( (4 - (-3))² + (-2 - 5)² )
= √(7² + (-7)²)
= √(98 + 49)
= √147
= 12.124
Therefore, the length of AB is approximately 12.124 units.
To learn more about Pythagorean theorem
https://brainly.com/question/28981380
#SPJ1
The mean annual salary for intermediate level executives is about $74000 per year with a standard deviation of $2500. A random sample of 36 intermediate level executives is selected. What is the probability that the mean annual salary of the sample is between $71000 and $73500?
Answers
Answer:
11.51% probability that the mean annual salary of the sample is between $71000 and $73500
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
\(\mu = 74000, \sigma = 2500, n = 36, s = \frac{2500}{\sqrt{36}} = 416.67\)
What is the probability that the mean annual salary of the sample is between $71000 and $73500?
This is the pvalue of Z when X = 73500 subtracted by the pvalue of Z when X = 71000. So
X = 73500
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{73500 - 74000}{416.67}\)
\(Z = -1.2\)
\(Z = -1.2\) has a pvalue of 0.1151
X = 71000
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{71000 - 74000}{416.67}\)
\(Z = -7.2\)
\(Z = -7.2\) has a pvalue of 0.
0.1151 - 0 = 0.1151
11.51% probability that the mean annual salary of the sample is between $71000 and $73500
A regional survey found that 60% of all families who indicated an intention to buy a new car bought a new car within 3 months, that 10% of families who did not indicate an intention to buy a new car bought one within 3 months, and that 26% indicated an intention to buy a new car. If a family chosen at random bought a car, find the probability (as a percent) that the family had not previously indicated an intention to buy a car. (Round your answer to two decimal places.)
Answers
Let A be the event that a family chose at random indicated an intention to buy a new car and let B be the event that a family chose at random bought a new car within 3 months.
We are asked to find P(A'), which is the probability that a family chosen at random had not previously indicated an intention to buy a car.
We can use the given information to write the following conditional probabilities:
P(B | A) = 60%
P(B | A') = 10%
P(A) = 26%
We can use these probabilities to apply Bayes' theorem to find P(A' | B), which is:
P(A' | B) = P(B | A') * P(A') / P(B)
Substituting the values from the problem, we have:
P(A' | B) = (10%) * (100% - 26%) / (60% * 26% + 10% * (100% - 26%))
= (10%) * (74%) / (60% * 26% + 10% * 74%)
= (10%) * (74%) / (15.4% + 7.4%)
= (10%) * (74%) / (22.8%)
= 43.86%
Therefore, the probability that a family chosen at random had not previously indicated an intention to buy a car is 43.86%.
Learn more about probability:
https://brainly.com/question/28021875
#SPJ4
a number m is no less than -1 or less than or equal to -5 1/3
Answers
Answer:
Step-by-step explanation:
y=5 1/3 can be expressed in infinite ways
PREMISES
y=5 1/3 expressed as a fraction
CALCULATIONS
The mixed number 5 1/3 can be written in various ways:
y=5 1/3
y=
(.25/.046875, .5/.09375, 1/.1875, 2/.375, 4/.75, 8/1.5, 16/3 as improper fractions or 5.3333 repeating as a decimal fraction]
The function
f(x) = 5sqrt(x + 13) + 5 has an inverse f ^ - 1 * (x) defined on the domain x < 5 Find the inverse. x >= - 13
Answers
The inverse function: \(f^{-1} (x) =\) \((\frac{x -5}{5} )^{2} -13\)
The inverse is defined on the domain x < 5 and x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5.
What is a function?A function is a relationship that exists between two sets of numbers, with each input from the first set, known as the domain, corresponding to only one output from the second set, known as the range.
Given function is; \(f(x) = 5\sqrt{(x + 13)} + 5\)
To find the inverse of the given function, we first replace f(x) with y:
⇒ \(y = 5\sqrt{(x + 13)} + 5\)
Subtract 5 from both sides:
⇒ \(y -5 = 5\sqrt{(x + 13)}\)
⇒ \(\frac{(y -5)}{5} = \sqrt{(x + 13)}\)
⇒ \((\frac{y -5}{5} )^{2} = x + 13\)
⇒ \((\frac{y -5}{5} )^{2} -13 = x\)
Now we have x in terms of y, so we can replace x with f⁻¹(x) and y with x to get the inverse function:
f⁻¹(x) = \((\frac{x -5}{5} )^{2} -13\)
The domain of the inverse function is x ≥ 5, because this is the range of the original function, and we were given that the inverse is defined on the domain x < 5. However, we must also exclude the value x = 5, because the denominator of the fraction \((\frac{x -5}{5} )^{2}\) becomes zero at this value. Therefore, the domain of f⁻¹(x) is x > 5.
We were given that x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5. Therefore, the domain of the inverse function becomes the range of the original function, and the range of the inverse function becomes the domain of the original function.
To know more about domain, visit:
https://brainly.com/question/26098895
#SPJ1
The weights of four similar packs of tomatoes are listed below.
Pack A: 2.456 pounds
Pack B: 2.457 pounds
Pack C: 2.454 pounds
Pack D: 2.459 pounds
Malcolm rounds the weights to the nearest hundredth pound. Which weight does
not round to 2.46 pounds?
A 2.456 pounds
B 2.457 pounds
C 2.454 pounds
D 2.459 pounds
Answers
Answer:
The weight that does not round to 2.46 pounds is C 2.454 pounds.
Step-by-step explanation:
Based on the given information, the weights of the four similar packs of tomatoes are as follows:
Pack A: 2.456 poundsPack B: 2.457 poundsPack C: 2.454 poundsPack D: 2.459 poundsMalcolm rounds the weights to the nearest hundredth pound. To round to the nearest hundredth pound, we look at the digit in the hundredths place. If it is 5 or greater, we round up the digit in the tenths place. If it is less than 5, we leave the digit in the tenths place as it is. Therefore, we can obtain the rounded weights as follows:
Pack A: 2.46 poundsPack B: 2.46 poundsPack C: 2.45 poundsPack D: 2.46 poundsFrom the above rounded weights, we see that Pack C rounds to 2.45 pounds and does not round to 2.46 pounds. Therefore, the weight that does not round to 2.46 pounds is C 2.454 pounds.
What is the range of f?
O -15≤x≤35
Oy > 15
Oy> 35
O all real numbers
Answers
The possible values for the range of f(x) are given by:
y > 15.y > 35.all real numbers.What is the range of a function f(x)?The range of a function f(x) is the set that contains all possible output values for the function. Looking at the graph of the function, the range is composed by the values of y.
In this problem, the function is not given, so I can't give you an exact answer, but since the range is composed by the values of y, the first option is not possible, and the possible values for the range of f(x) are given by:
y > 15.y > 35.all real numbers.More can be learned about the range of a function at https://brainly.com/question/28015028
#SPJ1
name of the vertex of <4 name the side of <1 write another name <5 classify each angle
Answers
Answer:
A. vertex B
B. Side BC and BD
C. Angle EBD
Step-by-step explanation:Me and my Teacher did this together
Find slope or line grab
Answers
Answer:
Step-by-step explanation:
divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those same 2 points .
How many hours in a year?
Answers
Answer:
Here is your answer hope it helps u have a great day ahead....

Find the GCF of 207c^3 and 108c^2
Answers
Answer: 9c²
Step-by-step explanation:
To find the Greatest Common Factor of 207c³ and 108c², first factor them down to their primes and see what they have in common.
207c³ 108c²
∧ ∧ ∧ ∧
9·23 c·c·c 9·12 c·c
∧ ∧ ∧
3·3 3·3 3·4
∧
2·2
207c³: 3·3·23 c·c·c
108c²: 2·2·3·3·3·4 c·c
GCF = 3·3 c·c
= 9c²
The GCF of 207c^3 and 108c² is 9c²
Given the expressions \(207c^3 \ and \ 108c^2\)
We are to find the GCF of both terms
First, we need to get the factors as shown::
207c³ = 9 * 23 * c² * c
108c² = 9 * 12 * c²
From the factors, we can see that 9 and c² are common to both terms:
The GCF of 207c^3 and 108c² is 9c²
Learn more here: https://brainly.com/question/21612147
PLS HELP The histogram displays donations in dollars to a charity. A histogram titled Donations to Charity In Dollars with the x-axis labeled Donations. The x-axis has intervals of 10 to 19, 20 to 29, 30 to 39, 40 to 49, and 50 to 59. The y-axis is labeled Number of Donations and starts at 0 with tick marks every one unit up to 5. There is a shaded bar above 10 to 19 that stops at 4, above 20 to 29 that stops at 3, above 30 to 39 that stops at 1, and above 50 to 59 that stops at 1. There is no shaded bar for 40 to 49. Which statement best describes the spread and distribution of the data?
The data is almost symmetric, with a maximum range of 49. This might happen if the charity suggested donation minimum of $35 and donors followed that.
The data is skewed, with a maximum range of 49. This might happen if the donations were only allowed in cash and many donors did not have much cash on them.
The data is bimodal, with a maximum range of 49. This might mean that the most popular amounts to donate were between 10 and 19 and 51 and 59 dollars.
The data is symmetric, with a maximum range of 59. This might happen if everyone donated a percent of their salaries.
Answers
Based on the given histogram, the data is skewed with a maximum range of 49.
This is because the frequency bars are not evenly distributed across the x-axis intervals, indicating that the data is not symmetric. The lack of a shaded bar for the 40 to 49 interval also suggests that there were fewer donations in that range compared to the other intervals.
One possible explanation for this skewness could be that the charity had suggested donation levels, with a minimum of $10, resulting in a large number of donations in the 10 to 19 interval. Additionally, the shaded bar stopping at 1 for the 30 to 39 and 50 to 59 intervals suggests that there were fewer donations in those ranges. This could be due to a variety of reasons, such as donors being more likely to give in the suggested $10 increments, or the charity's fundraising efforts being more effective at attracting donors in certain age or income brackets.
Overall, the histogram does not suggest a bimodal distribution, as there is not a clear separation between two distinct modes. The maximum range of 49 also indicates that there were no extreme outliers or large donations that would skew the data towards a higher range. Therefore, it is likely that the data represents a typical distribution of donations to a charity, with most donors giving smaller amounts and fewer donors giving larger amounts.
Learn more about histogram here:
https://brainly.com/question/30354484
#SPJ1
Factor this x2 − 2x + 3.
Answers
The quadratic expression x² − 2x + 3 cannot be factorized
How to factor the expressionFrom the question, we have the following parameters that can be used in our computation:
x² − 2x + 3
Rewrite as
f(x) = x² − 2x + 3
A quadratic expression is represented as
f(x) = ax² + bx + c
By comparison, we have
a = 1
b = -2
c = 3
The determinant (D) of the expression is calculated as
D = b² - 4ac
Substitute the known values in the above equation, so, we have the following representation
D = (-2)² - 4 * 1 * 3
Evaluate
D = -8
When the determinant of a quadratic expression is less than 0, the expression has no real root
This in other words mean that the expression cannot be factorized
The determinant, -8 is less than 0
So, x² − 2x + 3 cannot be factorized
Hence, the conclusion is that the expression x² − 2x + 3 cannot be factorized
Read more about factored expression at
https://brainly.com/question/723406
#SPJ1
can someone please help me

Answers
Answer: 19
Step-by-step explanation:
Type < or > to make this statement true -a___-b
Answers
The comparisons that are true are 11. -5 < 0 12. 9 > -8 14. 55 > -75 15. -32 < -24 16. 89 > 73 17. -58 < -51 19. 17 < 23 20. 18 > -36 and that is not true are 13. -7 = -7 (not true) 18. -32 > 4 (not true)
To make each statement true, write < or >. We need to compare two values for each statement to determine whether it is true or false.
To indicate that the first value is less than the second value, write <.
Alternatively, to indicate that the first value is greater than the second value, write >.
Below are the comparisons: 11. -5 < 0 12. 9 > -8 13. -7 > -7 14. 55 > -75 15. -32 < -24 16. 89 > 73 17. -58 < -51 18. -32 > 4 19. 17 > 23 20. 18 > -36
To determine the direction of inequality, we need to compare the values.
We used inequality signs such as > (greater than) or < (less than) to indicate which value is larger or smaller than the other.
For more questions on comparisons
https://brainly.com/question/30097421
#SPJ8
The correct question would be as
Write > or < to make each statement true.
11. -5 0
12. 9 -8
13. -7 7
14. 55 -75
15. -32 -24
16. 89 73
17. -58 -51
18. -32 4
19. 17 23
20. 18 -36
A football coach needs to divide 48 players into two groups.
He wants the ratio of players in Group 1 to players in Group 2 to be 1 to 3.
How many players will be in Group 2?
Answers
Answer:
36 players
Step-by-step explanation:
Total players = 48
Group 1 : Group 2
1:3
For Group 1:
=48X3÷4
=12
For Group 2:
=48X3÷4
=36
Group 1 players+Group 2 players=48 players
12+36=48
Solve the following 20!/17!
Answers
Answer:
6840
Step-by-step explanation:
20 ! = 20*19*18*17*.......1
17 =17*16*15*.....1
20!
-----
17!
20*19*18*17*.......1
---------------------------
17*16*15*.....1
Canceling like terms
20*19*18
------------
1
6840
Answer:
\(20!/17!\)
\(\frac{20!}{17!}=20\cdot \:19\cdot \:18\)
\(20\cdot \:19\cdot \:18=6840\)
\(OAmalOHopeO\)
