Answers
Answer:
Equation:
C = 1.75x + 5 25
A 22-mile ride costs $43.75.
Step-by-step explanation:
Because there is a flat fee of 5.25, only the first two equations could possibly be correct.
Then check with the examples given. If a 7 mile ride costs 17.50, the second equation cannot possibly be right. 7 miles times over $5 per mile will cost more than $35 not even including the flat fee.
Check:
1.75(7) + 5.25 = 17.50
and
12(1.75) + 5.25 = 26.25
So, the correct equation is
C = 1.75x + 5.25
Next use this equation to find the cost of the 22 mile ride.
1.75(22) + 5.25
= 43.75
Related Questions
In 32 days, a person saved $56. What was the person's average daily savings?
Answers
Answer: $ 1792
Step-by-step explanation:
The number 0.3333... repeats forever, therefore, it is irrational
Answers
Answer:
FALSE
Step-by-step explanation:
A repeating decimal is a rational number.
0.3333(repeating) = 1/3
__
A non-repeating infinite decimal is an irrational number. √2 and π are examples of such numbers.
Find the size of angle x.
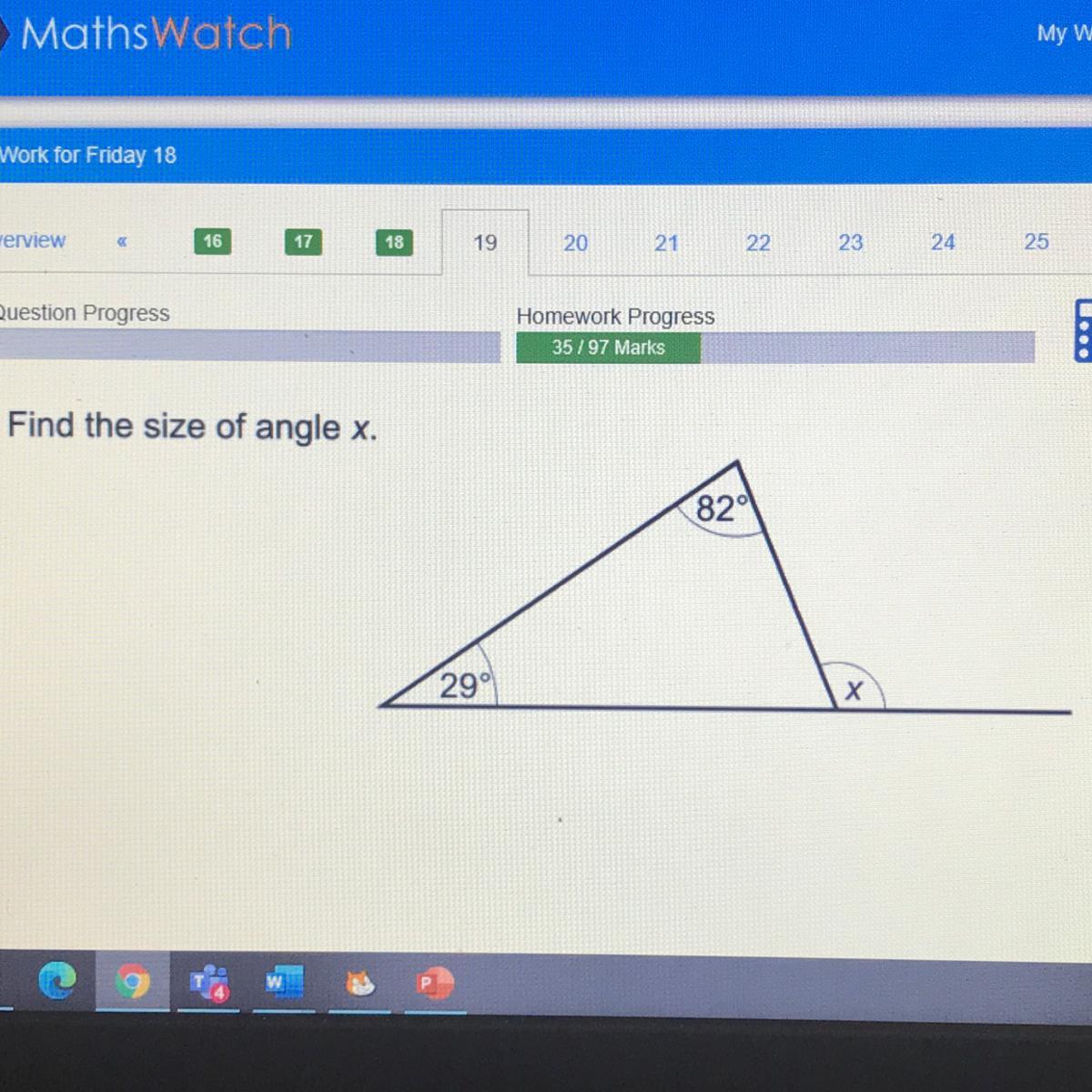
Answers
Answer:
x = 111
Step-by-step explanation:
180- 82 -29 is 69 and 180-69 is x which x is equal to 111
Answer:
111°
Step-by-step explanation:
By exterior angle theorem:
\(x = 82 \degree + 29 \degree \\ = 111 \degree\)
Find the missing lengths!!!!!!!

Answers
Answer:
13
Step-by-step explanation:
It is a square so the length of 1 side = \(\sqrt{169}\) = 13
Points A and B are on opposite sides of a lake. Another point, C. is 94.4 meters from Angle A. The measure of Angle A is 72° and the measure of Angle C is 30°. Find the distance between A and B.
Answers
To find the distance between points A and B, we can use trigonometry and the given information.
Let's label the distance between A and B as "d". We know that point C is 94.4 meters away from point A. From angle A, we have the measure of 72°, and from angle C, we have the measure of 30°.
Using trigonometry, we can use the tangent function to find the value of "d".
tan(72°) = d / 94.4
To solve for "d", we can rearrange the equation:
d = tan(72°) * 94.4
Using a calculator, we can evaluate the expression:
d ≈ 4.345 * 94.4
d ≈ 408.932
Therefore, the distance between points A and B is approximately 408.932 meters.
use the form of the definition of the integral given in theorem 4 to evaluate the integral. 21. y 5 2 s4 2 2xd dx
Answers
In the given question, using the form of the definition of the integral we have to evaluate the given integral.
The given integral is:
\(\int^{5}_{2}(4-2x)dx\)
A theorem that connects the ideas of differentiating a function and integrating a function is known as the fundamental theorem of calculus. With the exception of a constant value that relies on where one starts to compute area, the two procedures are inverses of one another.
We can write it as
\(\int^{5}_{2}(4-2x)dx=4\int^{5}_{2}dx-2\int^{5}_{2}xdx\)
Using the integral formula: \(\int{x^{n}dx} = \frac{x^{n+1}}{n+1}\)
\(\int^{5}_{2}(4-2x)dx=4[x]^{5}_{2}-2[x^2/2]^{5}_{2}\)
Now solving;
\(\int^{5}_{2}(4-2x)dx\) = 4[5-2]-2[{(5)^2-(2)^2/2]
\(\int^{5}_{2}(4-2x)dx\) = 4*3-2[(25-4)/2]
\(\int^{5}_{2}(4-2x)dx\) = 12-2[21/2]
\(\int^{5}_{2}(4-2x)dx\) = 12 - 21
\(\int^{5}_{2}(4-2x)dx\) = -9
To learn more about fundamental theorem of calculus link is here
brainly.com/question/2293034
#SPJ4
The right question is:
Use the form of the definition of the integral given in theorem 4 to evaluate the integral.
\(\int^{5}_{2}(4-2x)dx\)
twenty professiional athlets were asked what age did you graduate from college the responses are displayed in the histogram below
Answers
According to the given graph:
Age at graduation (in years) between 45 to 50 years.Age at graduation (in years) between 20 to 25 years.What is histogram?A histogram is a data representation that looks like a bar graph that bins a variety of classifications into columns and along the horizontal x-axis. The number count or percentage of occurrences inside this data for each column is represented by the vertical y-axis. Columns can be utilized to display data distribution patterns.
When should a histogram be used?When you're taking continuous measurements and you want to understand the distribution of results and look for outliers, use histograms. These graphs divide your continuous measurements into value ranges known as bins.
According to the given data:Based on these data, the numbers below appear to represent the smallest.:
= Age at graduation (in years) between 45 to 50 years.
Based on these data, the numbers below appear to represent the largest.
= Age at graduation (in years) between 20 to 25 years.
To know more about histogram visit:
https://brainly.com/question/16819077
#SPJ9
I understand that the question you are looking for is:
Twenty professional athletes were asked, “What age did you graduate from college?” The responses are displayed in the histogram below.
Frequency 20 30 Age at graduation (in years) 40 50
(a) Which of the statistics below appear to be the smallest based on these data?
(b) Which of the statistics below appear to be the largest based on these data?

graphing inequality's

Answers
Answer :
\(\boxed{\textsf {The red area is the required answer . }}\)
Step-by-step explanation:
A linear inequality in two variables is given to us and we need to plot it's graph .So the the given inequality is ,
\(\sf\implies y \geq- \dfrac{1}{5}x +5 \)
So firstly let's simplify out the inequality for easy plotting of the graph .
\(\sf\implies y \geq- \dfrac{1}{5}x +5 \\\\\sf\implies y \geq \dfrac{-x+5(-5)}{5}\\\\\sf\implies y \geq \dfrac{-x-25}{5}\\\\\sf\implies y \geq -(1)\dfrac{x+25}{5}\)
Now let's put some values of x to get values of y .
• Firstly put x = 0 then we get , y is greater than or equal to 0+5/5 (-1) = 5/5(-1) = -1 . Hence we get y ≥ (-1) .
• Secondly put x = 1 , then we get , y is greater than or equal to 1+5/5(-1)=6/5(-1) = -6/5 . Hence we get y ≥ -6/5 .
• Thirdly put x = -1 , then we get y is greater than or equal to -1+5/5(-1) = -4/5 . Hence we get y ≥ -4/5
• Fourthly put x = (-5) , then we get y is greater than or equal to -5+5/5(-1) = 0 .Hence we get y ≥ 0 .
With reference to these let's plot a graph . For the graph kindly refer to the attachment :) .
Here in the graph the red area shows the possible values of x and y .

You have several numbers in a data set: 5, 7, 9, 11, 13, 15, 17. What is the z Score for the number 15? (the SD is 4.32)
Answers
The value of the z-score for the number 15 in a data set is 0.93.
Define z-score.
A data point's z-score, also known as a standard score, indicates how far it deviates from the mean. In practical terms, however, it's a measurement of how many standard deviations a raw number is from or above the population mean.
You can plot a z-score on a normal distribution graph. Z-scores can be anywhere between -3 and +3 standard deviations.
∴ z = (x – μ) / σ
Given:
σ = 4.32
x = 15
Data set: 5, 7, 9, 11, 13, 15, 17
So, mean = 5 + 7 + 9 + 11 + 13 + 15 + 17/7
= 77/7
μ = 11
z = (x – μ) / σ
= (15 - 11)/4.32
= 4/4.32
z = 0.93
To know more about z-score visit:
brainly.com/question/15016913
#SPJ1
NO LINKS!! URGENT HELP PLEASE!!!
9. Find the equation of the PARABOLA with a vertex at (-2, 6) and passing through the point (1, -3)
Answers
Answer:
y= -x²-4x+2
Step-by-step explanation:
write in vertex form
a(x-h)²+k
in our case h = -2 and k= 6
y=a(x+2)²+6
now we just need to solve for a. we know that when x= 1 y = -3. plug these values in and solve for a
-3= a(1+2)²+6
-9=9a
a= -1
thus the formula is -(x+2)²+6
generally, teachers want things in standard form, so expand the exponent and simplify.
-(x²+4x+4)+6
y= -x²-4x+2
Answer:
\(y = -x^2 - 4x + 2\)
Step-by-step explanation:
The equation of a parabola in vertex form is:
\(y = a(x - h)^2 + k\)
where (h, k) is the vertex of the parabola.
In this case, the vertex is (-2, 6), so h = -2 and k = 6.
We also know that the parabola passes through the point (1, -3).
Plugging these values into the equation, we get:
\(-3 = a(1 - (-2))^2 + 6\)
\(-3 = a(3)^2 + 6\)
-9 = 9a
a = -1
Substituting a = -1 into the equation for a parabola in vertex form, we get the equation of the parabola:
\(y = -1(x + 2)^2 + 6\)
This equation can also be written as:
\(y = -x^2 - 4x -4+6\\y=x^2-4x+2\)
Write the equation of a line that is perpendicular to y = 2x +9
and passes through (-8, -2).
Answers
Answer:
is 17 la mejor respuesta
Consider the equation below.
-2(5x + 8) = 14 + 61
The equation was solved using the following steps.
-10r - 16 = 14 + 6r
Step 1:
Step 2:
Step 3:
-163 – 16 = 14
-16= 30
Step 4:
30
=
-16
Step 5:
1 =
Complete the statements below with the process used to achieve steps 1-4.
Answers
Answer:
x = -91/10
Step-by-step explanation:
-2(5x + 8) = 14 + 61
-10x -16 = 75
-10x = 91
-10x/-10 = 91/-10
x = -91/10
Rectangles abcd and klmn are similar. If their permitted are 20 and 16, and the area of the larger rectangle is 25, what is the area of the smaller rectangle?
Answers
The area of the smaller rectangle (KLMN) is 16.
Since rectangles ABCD and KLMN are similar, their corresponding sides are proportional.
Let's assume the length of side AB in rectangle ABCD is x, and the length of side KL in rectangle KLMN is y.
We can set up the proportion:
(x/y) = (20/16)
To find the area of the smaller rectangle, we need to determine the ratio of their areas.
Since the area of a rectangle is given by the product of its length and width, the ratio of the areas will be equal to the square of the ratio of their sides:
(Area of ABCD)/(Area of KLMN) = (x²)/(y²)
We are given that the area of ABCD is 25, so we have:
25/(Area of KLMN) = (x²)/(y²)
To find the area of KLMN, we need to substitute the values of x and y from the proportion:
25/(Area of KLMN) = (20/16)²
Simplifying the right side:
25/(Area of KLMN) = (5/4)²
25/(Area of KLMN) = 25/16
Cross-multiplying:
25 × 16 = 25 × (Area of KLMN)
400 = 25 × (Area of KLMN)
Dividing both sides by 25:
16 = Area of KLMN
Therefore, the area of the smaller rectangle (KLMN) is 16.
Learn more about similarity click;
https://brainly.com/question/26451866
#SPJ1
Find the weight in pounds of a 140-kilogram person. Round to the nearest hundredth.
Answers
Answer:
308.65 lb
Step-by-step explanation:
1 lb = 0.45359 kg
140 kg * (1 lb)/(0.45359 kg) = 308.65 lb
1 kilogram ≈ 2.205 pounds
Multiply.
140 * 2.205 = 308.70 pounds
Best of Luck!
DQ2 Do all linear transformations have a matrix representation? If so, what theorem establishes this? If not, provide a counter-example
Answers
Yes, This is established by the Rank-Nullity Theorem, A counter-example would be a transformation that is not linear.
Yes, all linear transformations have a matrix representation. The theorem that establishes this is the Matrix Representation Theorem. This theorem states that given a linear transformation T : V → W where V and W are vector spaces over a field F, then there is a unique matrix A such that T(v) = Av for any v in V. This theorem proves that any linear transformation can be represented by a matrix.
A counter-example of a linear transformation that does not have a matrix representation is a transformation that maps a vector in one vector space to a vector in a different vector space. For example, if V is a vector space over the field F, and W is a vector space over another field K, then the linear transformation T : V → W does not have a matrix representation since the size of the matrix would need to be different for each vector in the different vector spaces.
Learn more about linear here
https://brainly.com/question/27749345
#SPJ1
You are offered two different sales jobs. The first company offers a straight commission of 5% of the sales.
The second company offers a salary of $ 210 per week plus 2% of the sales. How much would you have to
sell in a week in order for the straight commission offer to be at least as good?
Answers
Answer:
The offers are equal at $7,000, after $7,000 more money will be made with a straight commission.
Step-by-step explanation:
.05x = .02x + 210 Subtract .02x from both sides.
.03x = 210 Divide both sides by .03
x = $7,000.
Multiply. Write your answer as a fraction in simplest form.
8
X
9

Answers
Answer:
40/54 = 20/27
Step-by-step explanation:
Look at question on the image

Answers
Answer: 170
Step-by-step explanation:
The formula for the area of a triangle is 1/2bh, where b is the base length, and h is the height.
So- Essentially you’d just need to plug in the variables to solve this. the semicircle on the bottom serves to tell you the base length.
1/2(20)(17)
170
Copy and complete the graphic organizer. List the types of triangles that can be solved by using each law. Consider the following types of triangles: ASA. AAS, SAS, SSA, and SSS. Law of Sines B. Enumerate the formulas for the Law of Cosines if the given is segitga ABC
Answers
The degree of angle C is approximately 150°.
Law of Sines:
ASA: SinA/a = SinB/b = SinC/c
AAS: SinA/a = SinB/b = SinC/c
SAS: SinA/a = SinB/b = SinC/c
SSA: SinA/a = SinB/b = SinC/c
SSS: SinA/a = SinB/b = SinC/c
Law of Cosines:
Segitga ABC: c² = a² + b² – 2ab cosC
The Law of Cosines is a mathematical formula that states that the square of the length of a triangle's longest side (c) is equal to the sum of the squares of the other two sides (a and b) minus twice the product of the other two sides and the cosine of the angle between them (C). To calculate the cosine of the angle (C) in segitga ABC, the following formula can be used: CosC = (a² + b² - c²) / 2ab. For example, if the length of side a is 3, the length of side b is 4, and the length of side c is 5, the cosine of angle C can be calculated as follows: CosC = (3² + 4² - 5²) / 2(3)(4) = -1/24. Therefore, the degree of angle C is approximately 150°.
Learn more about degree here:
https://brainly.com/question/14569348
#SPJ4
If the sales tax in Texas is 8.25%, what is the
total cost of a new backpack for $36?
Answers
Answer:
\(Total\ Cost = \$38.97\)
Step-by-step explanation:
Given
\(Backpack = \$36\)
\(Sales\ Tax = 8.25\%\)
Required
Determine the Total Cost
Total cost is calculated as thus
\(Total\ Cost = Backpack + Backpack * Sales\ Tax\)
\(Total\ Cost = \$36 + \$36 * 8.25\%\)
\(Total\ Cost = \$36 + \$2.97\)
\(Total\ Cost = \$38.97\)
Solve the following quadratic inequality x^2+x-6>0
Answers
Answer:
x < -3 or x > 2
Step-by-step explanation:
x² + x - 6 > 0
Convert the inequality to an equation.
x² + x - 6 = 0
Factor using the AC method and get:
(x - 2) (x + 3) = 0
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.
x - 2 = 0
x = 2
x + 3 = 0
x = -3
So, the solution is x < -3 or x > 2
Triniti had $500 in a savings account at the beginning of the summer. She withdraws $25 each week for food, clothes, and movie tickets. Write an inequality that represents Triniti’s situation and use w for the number of weeks. How many weeks can Triniti withdraw money in her account?
Answers
Answer:500-25x
Step-by-step explanation:
HELPPPPOMOGMGOGMGOGKM PLS ANSWER THIS CORRECTLY PLZZZ THIS IS FOR A VERY IMPORTANT TEST YOUWILL GET BRAINLIEST HELP

Answers
Answer:
i cant give u the answer but here is an example hope this helps slope = "rise over run" the difference in y values divided by the difference in x values
= 6/-3 = -2 = m. It's negative because as x increases, y decreases
plug that into the point slope formula, with either point. generally use the most simple point
y-h= m(x-k) where m= -2 and (k,h) = (2,-2)
y+2 = -2(x-2)
simply if you want
Y = -2x +4 -2 = -2x +2
or
2x +y = 2
Step-by-step explanation:
Answer:
Your slope is -1
Your y inter is -3
Step-by-step explanation:
Hope this helps you :)
The collection of natural numbers is an example of an element.
A.
True
B.
False
Answers
Hope this helps
The perimeter of the triangle is 6a + 3 units. Write an expression in simplest form for the length of Side 3.

Answers
Answer:
Side 3 = a - 2
Step-by-step explanation:
Perimeter of a ∆ = sum of all the sides of a triangle
Perimeter of the given ∆ = 6a + 3 units
Side 1 = 2(a + 3)
Side 2 = 3a - 1
Side 3 = ?
Therefore:
Side 3 = Perimeter - sum of side 1 and 2
Thus:
Side 3 = 6a + 3 - [2(a + 3) + (3a - 1)]
Side 3 = 6a + 3 - [2a + 6 + 3a - 1]
Side 3 = 6a + 3 - [5a + 5]
Side 3 = 6a + 3 - 5a - 5
Side 3 = a - 2
The length of the third side is a-2.
Given that:
Perimeter of triangle: 6a + 3
Length of first side: 2(a+3)
Length of second side: 3a -1
Let the length of the third side of the triangle be x.
Then as perimeter of a triangle is sum of lengths of all 3 sides of the triangle, thus we have:
\(2(a+3) + x + 3a -1 = 6a + 3\\\\x = 6a - 2a - 3a + 3 - 6 + 1\\\\x = a - 2\)
Thus we have length of the third side as a -2.
Learn more here:
https://brainly.com/question/24388271
Paperback books sell for $5.95 normally. The book shelf offers them for 15% off. How much do you save? What is the price of a paperback book at the book shelf?
Answers
Answer:
Use the given functions to set up and simplify
15
%
.
5.95
=
15
%
=
0.15
A 13 foot board is cut into 2 pieces, if one piece is x feet long express the other length in terms x
Answers
Answer:
if they are equal then it would be 6.5
Kimberly wants to buy a new pair of jeans. If the jeans were originally $48.00, but are on sale with a 20% discount, how much will Kimberly have to pay for the jeans?
Answers
Answer:
38.40
Step-by-step explanation:
48x .20=9.6
48-9.6=38.4
The amount of the money that Kimberly has to pay for the jeans will be $38.4.
What is the percentage?The quantity of anything is stated as though it were a fraction of a hundred. A quarter of 100 can be used to express the ratio.
Kimberly wants to buy a new pair of jeans.
If the jeans were originally $48.00, but are on sale with a 20% discount.
Then the amount of the money that Kimberly has to pay for the jeans will be
⇒ $48 (1 – 0.20)
⇒ $48 x 0.80
⇒ $38.4
More about the percentage link is given below.
https://brainly.com/question/8011401
#SPJ2
Segment WT = 9. Find the length of W'T' if WT is dilated with a scale factor of 5.
Answers
Answer: 45
Step-by-step explanation:
\(W'T'=(9)(5)=45\)
Evaluate 3x2 + 3x - 9, when x = 2
Answers
3x2 =6 +3(2)-9
= 3
Answer:
9
Step-by-step explanation:
3x^2 + 3x - 9
Substitute x = 2 into the equation.
3(2)^2 + 3(2) - 9
3(4) + 6 - 9
12 + 6 - 9
18 - 9 =
9
