PLAY AMOUNG US WITH ME PLZ FAZWQ
Answers
Answer:
OKAY!! :D
Step-by-step explanation:
Answer:
sorry cant
Step-by-step explanation:
Related Questions
Question Completion Status: QUESTION 9 How many subsets with at least 5 elements the set of cardinality 7 has? Give your answer in numerical form QUESTION 10 Which of the following is a coefficient of the term containing x7 in the binomial expansion of (2x-1) 11? Select ALL that applies. 42,240 28-(4) 128-(1¹4) 0-(17) 128 -128 QUESTION 11 Please show your work for Question 10 on paper and upload the image. Attach Fle Click Save and Submit to save and submit. Click Save All Answers to save all answers 2104223_1&content_id=_66717882_18
Answers
The formula to find the number of subsets with at least k elements is given by nCk+1 − 1.So, the number of subsets with at least 5 elements the set of cardinality 7 has is: nC5+1 − 1 = 7C6 − 1 = 7 − 1 = 6.
The formula to find the number of subsets with at least k elements is given by nCk+1 − 1, where n is the number of elements in the set. The derivation is given below:Let S be a set with n elements.We want to find the number of subsets of S with at least k elements. For this, we can use the complement of the event "subset with at least k elements". The complement is "subset with less than k elements".Now, a subset of S can have 0 elements, 1 element, 2 elements, ..., n elements. Hence, the total number of subsets of S is 2n.Let's count the number of subsets of S with less than k elements. A subset of S with less than k elements can have 0 elements, 1 element, 2 elements, ..., k-1 elements. Hence, the total number of subsets of S with less than k elements is: 2^0 + 2^1 + 2^2 + ... + 2^(k-1) = 2^k − 1 (using the formula for sum of geometric series) Therefore, the number of subsets of S with at least k elements is given by the complement: 2n − (2^k − 1) = 2n − 2^k + 1 = nCk+1 − 1 (using the formula for sum of binomial series).Hence, the number of subsets with at least 5 elements the set of cardinality 7 has is: nC5+1 − 1 = 7C6 − 1 = 7 − 1 = 6.
Therefore, the number of subsets with at least 5 elements the set of cardinality 7 has is 6. In the binomial expansion of (2x-1)11, the term containing x7 is -4624x7. The coefficient of x7 is -4624. Option D is correct. The binomial expansion of (2x-1)11 is given by: (2x-1)11 = 1(2x)11 − 11(2x)10 + 55(2x)9 − 165(2x)8 + 330(2x)7 − 462(2x)6 + 462(2x)5 − 330(2x)4 + 165(2x)3 − 55(2x)2 + 11(2x) − 1 The general term in the binomial expansion is given by: T(r+1) = nCr prqn-r Here, n = 11, p = 2x, q = -1 For the term containing x7, r+1 = 8. Therefore, r = 7. T(8) = 11C7 (2x)7 (-1)^4 = 330x7 Thus, the coefficient of x7 is 330. But the coefficient of -x7 is -330.So, the term containing x7 is -330x7. Hence, the coefficient of x7 is -330 × -1 = 330.
Therefore, the coefficient of the term containing x7 in the binomial expansion of (2x-1)11 is 330.
To know more about cardinality visit:
brainly.com/question/29093097
#SPJ11
determine whatever ABCD is a parallelogram by using the midpoint formula.
A(3,3) B (1.2) C(-3.1) D (-1.4)

Answers
Answer:
Not a parallelogram.
Step-by-step explanation:
By the midpoint formula, the midpoint of a segment between \((x_{0},\, y_{0})\) and \((x_{1},\, y_{1})\) is:
\(\begin{aligned} \left(\frac{x_{0} + x_{1}}{2},\, \frac{y_{0} + y_{1}}{2}\right)\end{aligned}\).
A quadrilateral is a parallelogram if and only if the midpoints of the two diagonals are the same.
The two diagonals of quadrilateral \({\sf ABCD}\) are segment \(\sf{AC}\) and segment \({\sf BD}\), respectively.
Using the midpoint formula, the midpoint of segment \({\sf AC}\) (between \({\sf A}\; (3,\, 3)\) and \({\sf C}\; (-3,\, 1)\)) would be:
\(\begin{aligned} & \left(\frac{3 + (-3)}{2},\, \frac{3 + 1}{2}\right) \\ =\; & (0,\, 2)\end{aligned}\).
Likewise, the midpoint of segment \({\sf BD}\) (between \({\sf B}\; (1,\, 2)\) and \({\sf D}\; (-1,\, 4)\) would be \((0,\, 3)\).
Thus, quadrilateral \({\sf ABCD}\) would not be a parallelogram since the midpoints of its two diagonals are not the same.
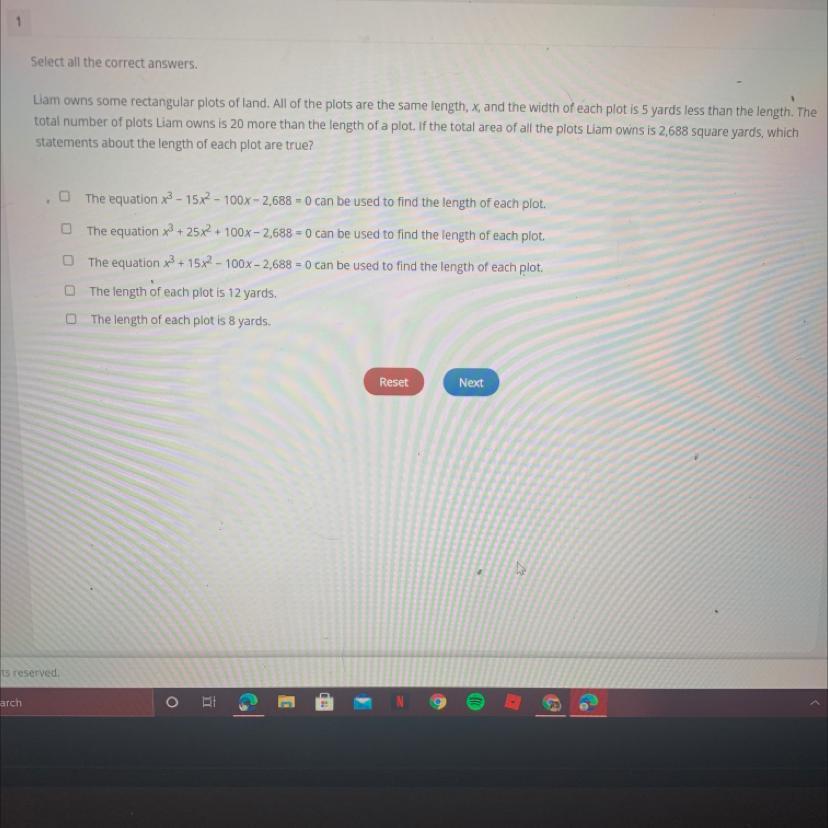
(PLEASE HELP 30 POINTS)
Select all the correct answers.
Liam owns some rectangular plots of land. All of the plots are the same length, x, and the width of each plot is 5 yards less than the length. The
total number of plots Liam owns is 20 more than the length of a plot. If the total area of all the plots Liam owns is 2,688 square yards, which
statements about the length of each plot are true?
The equation x3 - 15x2 - 100x - 2,688 0 can be used to find the length of each plot.
The equation x3 + 25x2 + 100% -2,688 = 0 can be used to find the length of each plot.
o o o o o
The equation x3 + 15x2 - 100x - 2,688 = 0 can be used to find the length of each plot.
The length of each plot is 12 yards.
The length of each plot is 8 yards.
Answers
Answer:
We have to:
"All of the plots are the same length, x"
L = x
"and the width of each plot is 5 yards less than the length"
W = x-5
"The total number of plots Liam owns is 20 more than the length of a plot"
20 + x
"the total area of all the plots Liam owns is 2,688 square yards"
A = (20 + x) * (x) * (x-5)
A = (20x - 100 + x ^ 2 -5x) * (x)
A = (x ^ 2 + 15x - 100) * (x)
2688 = (x ^ 3 + 15x ^ 2 - 100x)
x ^ 3 + 15x ^ 2 - 100x = 2688
x ^ 3 + 15x ^ 2 - 100x - 2688 = 0
Answer:
*** The equation x3 + 15x2 - 100x - 2.688 = 0 can be used to find the length of each plot.
Answer:x^3+15x^2-100x-2,688=0
Step-by-step explanation:
Sep,
At a sale, dresses were sold for 95% of their original
price. If the dresses originally cost $200 each, how
much did a dress cost on sale?
Answer:
Submit Answer
Answers
Answer:
$10
Step-by-step explanation:
200*0.05=10
Answer:
$10
Step-by-step explanation:
90% = 0.95
200×0.95= 190
200-190=10
Help me please! Late homework

Answers
2)Main Answer: a)1,8,27,64,125,216,343,512
b)I,II,III,IV,V,VI,VII,VIII,IX,X,XI
Concept and definitions should be there:
A conjecture is an educated guess that is based on known information. Example. If we are given information about the quantity and formation of section 1, 2 and 3 of stars our conjecture would be as follows.
Given data
a)Next five terms 1,8,27,64
b)Next five terms I,II,III,IV,V
Solving part
using conjecture
a)Next five terms 1,8,27,64,125,216,343,512
Notice that the difference between consecutive terms is 7.
Conjecture: n3, n=1,2,3...
Final Answer:1,8,27,64,125,216,343,512
b))Next five terms I,II,III,IV,V,VI,VII,VIII,IX,X,XI
Conjecture: n, n=i,ii,iii,...
Final Answe:I,II,III,IV,V,VI,VII,VIII,IX,X,XI
To learn about more about the reciprocal of the divisor visit:brainly.com/question/11054655 #SPJ9.
3)Quastion incompleted
4)Main answer :The number 14 is even and therefore is divisible by 2. This is the correct statement.
Given data
The statement which uses deductive reasoning to draw the conclusion is C. The number 14 is even and therefore is divisible by 2.
Solving part
The number 14 is even and therefore is divisible by 2. This is the correct statement.
Final Answer:The number 14 is even and therefore is divisible by 2. This is the correct statement.
To learn about more about the reciprocal of the divisor visit:brainly.com/question/23829807 #SPJ9.
5)Main Answer:X = -2
Concept and definitions should be there:This solution deals with linear equations with one unknown.
Given data
18x-2(3x+1)=5x-16
Solving part
We simplify the equation first:
18x−2(3x+1)=5x−16
18x+(−2)(3x)+(−2)(1)=5x+−16 (Distribute)
18x+−6x+−2=5x+−16
(18x+−6x)+(−2)=5x−16 (Combine Like Terms)
12x+−2=5x−16
12x−2=5x−16
Then we cancel out:
12x−2−5x=5x−16−5x
7x−2=−16
7x−2+2=−16+2
7x=−14
7x/7 = −14/7
x = -2
Final Answer:x = -2
To learn about more about the reciprocal of the divisor visit: brainly.com/question/13309562 #SPJ9.
3x+y=-8 Find the equation of a line perpendicular to the above line.
Answers
Answer:
y = 1/3x
Step-by-step explanation:
use a slope that is the opposite and reciprocal of -3, which would be 1/3
The selling price of a $10,000 5-year bond will be less than $10,000 if the A. Coupon rate is less than the market interest rate B. Coupon rate is greater than the market interest rate C. Coupon rate is equal to the market interest rate D. Maturity date is less than 5 years
Answers
The correct answer is A. The selling price of a bond is affected by the coupon rate and the market interest rate.
If the coupon rate is less than the market interest rate, investors will not be interested in buying the bond because they can get a higher return elsewhere. This results in the selling price of the bond being less than its face value of $10,000.
The selling price of a $10,000 5-year bond will be less than $10,000 if the:
A. Coupon rate is less than the market interest rate
This is because when the coupon rate (the interest paid by the bond) is lower than the market interest rate, investors would prefer to invest in other options that offer a higher return. Therefore, to attract buyers, the bond's selling price would be discounted to compensate for the lower coupon rate.
Learn more about price:
brainly.com/question/19091385
#SPJ11
Will give brainliest need quick answers

Answers
Answer:
u=1
v = 10
Step-by-step explanation:
For the triangles to be congruent
IG = PR
50 = u+49
50 - 49 = u
1 = u
GH = RQ
v+6 = 16
v = 16-6
v = 10
Please help meeeeeee

Answers
Answer:
see below
Step-by-step explanation:
$178 x .05 = $8.90 discount nearest hundredth
$178 - $8.90 = $169.10 sale price nearest hundredth
the half-life of radium-226 is 1600 years. suppose we have a 27-mg sample. (a) how much of the sample will remain after 4500 years? (round your answer to one decimal place.) mg (b) after how many years will only 15 mg of the sample remain? (round your answer to one decimal place.) yr
Answers
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
The result is obtained by using the exponential decay equation.
What is the exponential decay equation?The exponential decay equation can be used to calculate radioactive decay for the activity, the nuclei, and also the mass. The exponential decay equation for the mass is
\(m = m_{o} e^{-\lambda t}\)
Where
m = the initial massm₀ = the remaining massλ = decay constant (0.693/T½)T½ = half-lifet = decay timeThe half-life of radium-226 is 1600 years and the mass of a sample is 27 mg.
(a) What is the remaining mass after 4500 years?
(b) What is the decay time if the remaining mass is 15 mg?
First, let's calculate the decay constant.
λ = 0.693/T½
λ = 0.693/1600
λ = 0,000433
After 4500 years, the remaining mass is
\(m = m_{o} e^{-\lambda t}\)
\(m = 27 e^{-0.000433 \times 4500}\)
m = 27 × 0.142
m = 3.8 mg
If the remaining mass is 15 mg, the decay time is
\(m = m_{o} e^{-\lambda t}\)
\(15 = 27 e^{-0.000433 t}\)
\(ln \frac{15}{27} = ln (e^{-0.000433 t})\)
\(ln \frac{15}{27} = -0.000433 t\)
-0.588 = - 0.000433t
t = 1357.9 years
Hence,
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
Learn more about radioactive decay here:
brainly.com/question/9796067
#SPJ4
14 / 19 Marks
61%
.
Some of the children at a school arrive by car.
30% of the children at the school are boys.
• 60% of the boys at the school arrive by car.
• 80% of the girls at the school arrive by car.
What is the probability that a child chosen
at random from the school arrives by car? I
Give your answer as a decimal.
Answers
Answer:
Decimal version: 71%
Percentage version: 0.71
Step-by-step explanation:
You can build a two-way relative frequency table to represent the data:
These are the columns and rows:
Car No car Total
Boys
Girl
Total
Fill the table
30% of the children at the school are boys
Car No car Total
Boys 30%
Girl
Total
60% of the boys at the school arrive by car
That is 60% of 30% = 0.6 × 30% = 18%
Car No car Total
Boys 18% 30%
Girls
Total
By difference you can fill the cell of Boy and No car: 30% - 18% = 12%
Car No car Total
Boy 18% 12% 30%
Girl
Total
Also, you know that the grand total is 100%
Car No car Total
Boy 18% 12% 30%
Girl
Total 100%
By difference you fill the total of Girls: 100% - 30% = 70%
Car No car Total
Boy 18% 12% 30%
Girl 70%
Total 100%
80% of the girls at the school arrive by car
That is 80% of 70% = 0.8 × 70% = 56%
Car No car Total
Boy 18% 12% 30%
Girl 56% 70%
Total 100%
Now you can finish filling in the whole table calculating the differences:
Car No car Total
Boy 18% 12% 30%
Girl 56% 14% 70%
Total 74% 26% 100%
Having the table completed you can find any relevant probability.
The probability that a child chosen at random from the school arrives by car is the total of the column Car: 74%.
That is because that column represents the percent of boys and girls that that arrive by car: 18% of the boys, 56% of the girls, and 74% of all the the children.
IF YOU SOLVE THIS CORRECTLY WITH EXPLANATION U WILL GET BRAINILEST
-2r(8r+5)
Answers
Answer:
-16r^2 - 10r
Step-by-step explanation:
To simplify the expression -2r(8r+5), you can use the distributive property of multiplication over addition.
-2r(8r+5) = -2r * 8r - 2r * 5
First, let's simplify -2r * 8r:
-2r * 8r = -16r^2
Next, let's simplify -2r * 5:
-2r * 5 = -10r
Putting it all together, the simplified expression is:
-2r(8r+5) = -16r^2 - 10r
What is a displacement vector? How does this differ from distance?
How does this relate to velocity vs speed when considering both average and insantaneous.
Answers
A displacement vector is a vector that represents the overall change in position of an object, taking into account both the direction and magnitude of the change. It is a measurement of the distance and direction from an object's initial position to its final position.
Distance, on the other hand, is a scalar quantity that refers to the total amount of ground covered by an object, regardless of its direction. It is simply a numerical value indicating the length of the path traveled by an object.
When considering velocity vs speed, velocity is also a vector quantity that includes both the speed and direction of an object's motion. Average velocity is calculated by dividing the total displacement of an object by the time it took to travel that distance.
Average speed, however, is calculated by dividing the total distance traveled by the time it took to travel that distance.
Instantaneous velocity refers to the velocity of an object at a specific point in time, while instantaneous speed refers to the speed of an object at a specific point in time.
Both of these values can be calculated by taking the derivative of the object's position vs time graph. Overall, the difference between displacement and distance is that displacement takes direction into account, while distance does not. And when considering velocity vs speed, velocity includes both direction and speed, while speed only includes the numerical value of the distance traveled over time.
Learn more about displacement vector,
https://brainly.com/question/30615410
#SPJ11
Solve the inequality 2x - 3
Need help.... plz
Answers
Answer:
x=3/2
Step-by-step explanation:
2x-3=0
2x=0+3
2x=3
x=3/2
2x = 0 + 3
2x = 3
X = 3/2 , 1.5
7e4t + 200 = 2e4t +1500
Answers
-2e4t on both sides
5e+200=1500
-200 on both sides
5e=1300
divide 1300 by 5
e=260
YALL HELP‼️‼️‼️
It says to find the missing side of the triangle⁉️

Answers
Hi there!
you can use the Pythageron Therom for this one.
Basically you just need to apply this formula: a^2 + b^2 = c^2
And then find the root of the hypotenuse.
So, 15^2 + 8^2 = the hypotenuse^2
Which equals, 225 + 64 = 289
Square root of 289 = 17
17 is the answer you are looking for!
Please mark me brainliest if this helps!
Have a wonderful day!
What is the slope-intercept equation of the line below?

Answers
Answer:
C
Step-by-step explanation:
y=mx+b m=slope b=y-intercept, y-int: 4 slope: 3/1 but can just be put as 3. y=3x+4 bc it's a positive slope with a positive y-int.
Find the measure of each angle in
the problem.
RF contains noint P.

Answers
Answer:
1st option
Step-by-step explanation:
3z and 2z are adjacent angles on a straight line and sum to 180° , that is
3z + 2z = 180
5z = 180 ( divide both sides by 5 )
z = 36
Then
3z = 3 × 36 = 108°
2z = 2 × 36 = 72°
Solve the differential equation by variation of parameters. y + 2y' + y = e^-t ln t y(t)=
Answers
The general integral is provided by y = C1e-t + C2te-t + (1/2)(t2)e-t.
(m + 1)2 =0 is the characteristic polynomial for the differential equation y" +2y' + y = e-t.
Roots -1, -1. yh = C1e-t + C2te-t is the answer to the homogeneous equation at that point.
Use the method of variation of parameters, taking into account the independent integrals y1 = e-t, y2 = te-t, and Wronskian
W(t) = e-2t, to derive the specific integral related to f(t) = e-t.
Then, use the conventional formula yp = - y1(t)(Integral of Y2(t)f(t)dt/W(t)) +y
Obtain yp = (1/2)(t2)e-t for the given situation.
As a result, the general integral is provided by
y = C1e-t + C2te-t + (1/2)(t2)e-t.
Know more about equation at:
https://brainly.com/question/2972832
#SPJ4
utiliza la formula de la distancia para calcular la medida de los segmentos A(6,8)yB(3,4)AB=
Answers
Answer:
5.
Step-by-Step explanation:
Distance = √ [(6-3)^2 + (8-4)^2) ]
= √(9 + 16)
= √25
= 5.
The table shows a function what is the range of the function?
Answers
The range of the function f(x) = 2x^2 - 3x + 5 is (5/8, ∞).
To find the range of the function f(x) = 2x^2 - 3x + 5, we need to determine the set of all possible output values (y-values) for the corresponding input values (x-values). The range represents the set of all possible y-values.
One way to approach this is by considering the graph of the function, which is a parabola that opens upward since the coefficient of the x^2 term is positive. Since there is no restriction on the x-values, the parabola extends infinitely in both directions. Therefore, the range of the function is also infinite.
Mathematically, we can confirm this by considering the vertex of the parabola. The x-coordinate of the vertex can be found using the formula x = -b/2a, where a and b are the coefficients of the quadratic terms. In this case, a = 2 and b = -3, so x = -(-3)/(2*2) = 3/4. Substituting this value back into the function, we find that f(3/4) = 5/8.
Since the function is a parabola that opens upward, the y-values increase without bound as x approaches infinity. Therefore, the range of the function is (5/8, ∞).
Complete question should be What is the range of the function f(x) = 2x^2 - 3x + 5?
For more questions on function
https://brainly.com/question/29631554
#SPJ8
Identify the slope shown in the linear equation below. y = - 5x + 3
Answers
Answer:
Slope: -5 Y-intercept: 3
Step-by-step explanation:
the slope intercept of a linear equation is:
y=mx+b
were m is slope. and b is the y intercept
therfore the problem is:
y=-5x+3
m=-5 so the slope is -5
b=3 so the y-intrercept is 3
Answer:
-5
Step-by-step explanation:
The slope is always in front of the x
List the characteristics of a proportinonal relationship
Answers
Answer:
Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other. That constant is know as the "constant of proportionality".
The two requirements for a proportional relationship are: The ratio of the two variables maintain the same ratio.
write the equation for a parabola with a focus at (0,-5) and a directrix at y=-3
Answers
All done
Given the general identity tan X = , which equation relating the acute angles, A and C, of a right ∆ABC is true?
Answers
Answer:
A. tan A = sin A / sin C
Step-by-step explanation:
Answer:
tan A = sin A / sin C
Step-by-step explanation:

Determine whether the paired values represent a proportional relationship.
(-2,-4).(-1, - 2).(1, 2).(2, 4)
Answers
Answer:
(-1,-2) is the correct one but they all are the same
Find the work done by the force field
F(x, y, z) =
on a particle that moves along the line segment from (0, 0, 1) to (2, 1, 0).
Answers
The work done by the force field F along the line segment from (0, 0, 1) to (2, 1, 0) is 1/3.
The work done by a force field F along a curve C is given by the line integral:
W = ∫C F · dr
where dr is the differential of the position vector r(t) along the curve, and the dot (·) represents the dot product.
In this case, the curve C is the line segment from (0, 0, 1) to (2, 1, 0), which we can parameterize as:
r(t) = <2t, t, 1 - t> for 0 ≤ t ≤ 1.
The differential of r(t) is:
dr = <2, 1, -1> dt
The force field F(x, y, z) = <yz, xz, xy>, so we can evaluate F at each point along the curve to obtain:
F(r(t)) = <t, 2t(1 - t), t>
Finally, we can compute the dot product F · dr:
F · dr = <t, 2t(1 - t), t> · <2, 1, -1> dt
= 2t + 2t(1 - t) - t dt
= 2t - 2t^2 dt
Integrating this expression over the interval [0, 1], we get:
∫C F · dr = ∫0^1 (2t - 2t^2) dt
= [t^2 - (2/3)t^3]0^1
= 1 - (2/3)
= 1/3
Therefore, the work done by the force field F along the line segment from (0, 0, 1) to (2, 1, 0) is 1/3.
To learn more about work done visit:
brainly.com/question/25573309
which of the following statements about huffman greedy algorithm are true? assume
Answers
a) A symbol with a frequency of at least 0.4 will never be encoded with two or more bits. - True
b) A symbol with a frequency of at least 0.5 will never be encoded with two or more bits. - False
c) If all symbol frequencies are less than 0.33, all symbols will be encoded with at least two bits. - False
d) If all symbol frequencies are less than 0.5, all symbols will be encoded with at least two bits. - True
a) The Huffman greedy algorithm assigns shorter codes to symbols with higher frequencies. Therefore, a symbol with a frequency of at least 0.4 will never be encoded with two or more bits because it has a higher frequency and will be assigned a shorter code.
b) This statement is false. The Huffman greedy algorithm does not guarantee that a symbol with a frequency of at least 0.5 will always be encoded with a single bit. The encoding depends on the distribution of frequencies and the construction of the Huffman tree.
c) This statement is false. If all symbol frequencies are less than 0.33, it is possible that some symbols will be encoded with a single bit if they have a high frequency, while others may be encoded with more than two bits depending on their frequencies.
d) This statement is true. If all symbol frequencies are less than 0.5, the Huffman greedy algorithm guarantees that all symbols will be encoded with at least two bits. This is because the algorithm assigns shorter codes to symbols with higher frequencies, and since all frequencies are less than 0.5, none of the symbols will have a high enough frequency to be encoded with a single bit.
To learn more about Huffman greedy algorithm click here:
brainly.com/question/29898146
#SPJ11
Which graph represents a system of equations with one solution?
Answers
This graph represent a system of equation with one solution. The blue point is the solution.
Hope this helps ^◇^

Find the slope of the points (2, 13) and (8, 1)
Answers
y2-y1/x2-x1
take the y coordinate of the second pair of coordinates and subtract it by the y coordinate of the first pair, then take the x coordinate from the second pair of coordinates and subtract it from the x coordinate from the first pair. then put your answer from the y coordinate over the answer from the x coordinates. 1 - 13 / 8 - 2, then you get -12/6, which simplifies to 2.
Hope this helps :)