Parker drank 36 fluid ounces of a sports drink at her basketball game. How many pints did she drink
Answers
Answer:
2 1/4 pints
Step-by-step explanation:
create a ratio with the fact there are 16 ounces in 1 cup
let 'p' = number of pints
16 = 36
1 p
cross-multiply: 16p = 36
p = 36/ 16, which is 9/ 4, or 2 1/4
Related Questions
Michal got a $50 gift card to an online music store. He bought an $10 album.He wants to buy songs that cost $1.25? Per song. Write and some solve an inequality to find the most songs he can.
Answers
Answer:
Step-by-step explanation:
Step-by-step explanation:
Given that:
Worth of gift card = $50
Cost of album purchased = $10.00
Cost per song to purchase = $1.25
Number of songs to purchase = n
Inequality to model the situation :
Cost of album + cost per song * (Number of songs) ≤ worth of gift card
$10.00 + ($1.25 * n) ≤ $50
$10.00 + $1.25n ≤ $50
Which of the following Statements are true?
Statement 1: A STOP sign is a regular
octagon.
Statement 2: An equilateral triangle has
three angles.

Answers
Answer:
C. Both statements are true
A bus driver makes 31309.02 a year. If they get paid weekly, how much do they get each paycheck? Round to the nearest cent
Answers
Answer:
Step-by-step explanation:
651
Answer:
$602.1/week
Step-by-step explanation:
There are 52 weeks in a year.
31309.02 / 52 = 602.0965..
AKA : $602.1 per week
determine the number of line segments in the hundredth pattern
(its the triangle one, starts with one then two then three …..
Answers
There are 4850 line segments in the hundredth pattern of the triangular number sequence.
The pattern you're referring to is often called the triangular number sequence. In this sequence, each term represents the number of dots required to form an equilateral triangle with sides of increasing length. To determine the number of line segments in the hundredth pattern, we need to consider the number of sides and diagonals in each triangle.
Let's analyze the pattern step by step:
Pattern 1:
The first pattern consists of a single dot, which does not form any line segments.
Pattern 2:
The second pattern consists of three dots forming an equilateral triangle. It has three sides.
Pattern 3:
The third pattern consists of six dots forming an equilateral triangle. It has three sides and three diagonals.
Pattern 4:
The fourth pattern consists of ten dots forming an equilateral triangle. It has three sides and six diagonals.
We can observe that for each pattern, the number of sides remains constant at 3. However, the number of diagonals increases by one with each pattern. The formula to calculate the number of diagonals in an equilateral triangle is given by:
Number of diagonals = (n * (n - 3)) / 2,
where n represents the number of sides (which is 3 in the case of an equilateral triangle).
Using this formula, we can calculate the number of diagonals for the hundredth pattern:
Number of diagonals = (100 * (100 - 3)) / 2
= (100 * 97) / 2
= 4850.
Since each diagonal forms a line segment, the number of line segments in the hundredth pattern is equal to the number of diagonals, which is 4850.
Therefore, there are 4850 line segments in the hundredth pattern of the triangular number sequence.
For more such questions on line segments visit:
https://brainly.com/question/2437195
#SPJ8
Grace rides the bus to her grandmother's house each day. A one way trip is 8.12 miles. How many miles does
she travel after 5 days help on 1 and 2 please extra points

Answers
40.6 miles and $9.77
Step-by-step explanation:
[Number 1]
8.12 × 5
= 40.6 miles
[Number 2]
2.79 × 3 ½
= 2.79 × 3.5
= 9.765
≈ $ 9.77
HELPPP!!! PLEASEEEEEEE

Answers
Answer:
Step-by-step explanation:
37
2, 5, 8, 11, 14,... ... ... ....
a30
What’s the missing term
Answers
Answer:
17, 20, 23, 26, 29, 32,
Step-by-step explanation:
Answer:
17, 20, 23, 26, 29, 32, 35....
Step-by-step explanation:
cause that's how math was made
"don't have a good day, have a great day"
-Guy
Help ASAP! And explain!
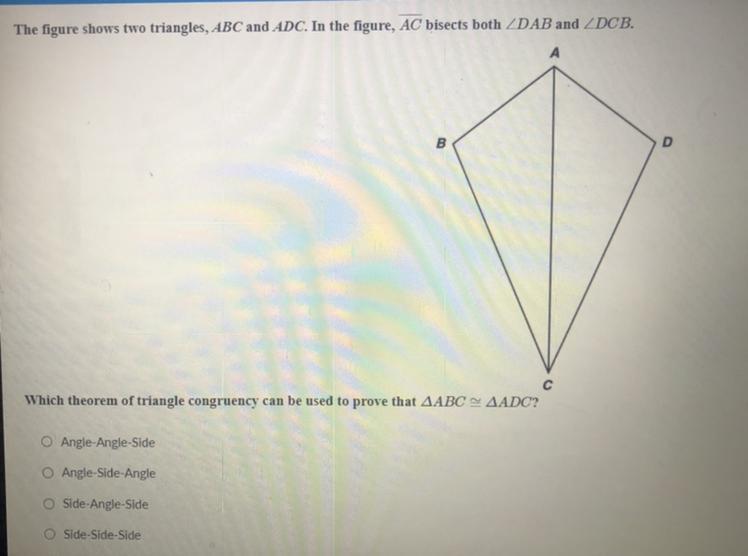
Answers
Answer: B) Angle-Side-Angle
This abbreviates to ASA.
============================================
Explanation:
We're told that segment AC bisects angle DAB. This means angle DAB is cut into two equal halves. Those two smaller equal angles are angle DAC and angle CAB. So we can say angle DAC = angle CAB.
Also, we're told that segment AC bisects angle DCB. This means angle DCA = angle ACB
Lastly, through the reflexive property, we know that AC = AC. Any segment is congruent to itself.
These three facts allow use to use ASA. Note how the congruent sides are between the congruent angles mentioned. With ASA, the "S" is between the "A"s to reflect this.
-------------
We can break things down like this:
A: angle DAC = angle CABS: segment AC = segment ACA: angle DCA = angle ACBThe order matters and ASA is slightly different from AAS. In the case of AAS, the side is not between the angles.
Susan is running a 5k race. The graph of distance vs. time is shown.
What interval is she running the fastest?

Answers
The interval of the graph at which Susan is running fastest is from point A ( 0 , 0 ) to B ( 10 , 3 )
Given data ,
Susan is running a 5k race. The graph of distance vs. time is shown
So , the slope of the first line is m₁
And , the slope of the second line is m₂
where the points are A ( 0 , 0 ) , B ( 10 , 3 ) , C ( 20 , 4 )
Now , slope of AB is
m₁ = ( 3/10 ) = 0.3
And , m₁ = 0.3 kilometers per minute
And , slope of BC is
m₂ = ( 4 - 3 ) / ( 20 - 10 )
m₂ = 1/10
m₂ = 0.1 kilometers per minute
Therefore , the interval is fastest at second line from B ( 10 , 3 ) , C ( 20 , 4 )
Hence , Susan is running fastest is from point A ( 0 , 0 ) to B ( 10 , 3 )
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ1
Find the equation of the hyperbola that has foci at (±3,0) and vertices at (±2,0).
Answers
The equation of the hyperbola with foci at (±3,0) and vertices at (±2,0) is\((x^2 / 4) - (y^2 / 5) = 1\).
To find the equation of a hyperbola, we need to determine its center, vertices, and foci. In this case, we can observe that the hyperbola is centered at the origin (0, 0) since the foci and vertices lie along the x-axis.
Let's denote the distance between the center and each focus as c, and the distance between the center and each vertex as a. In this scenario, the foci are located at (±3, 0), and the vertices are at (±2, 0).
From the given information, we can deduce that c = 3 and a = 2. Now, we can calculate the value of b using the relationship between a, b, and c in a hyperbola:
\(c^2 = a^2 + b^2\)
Plugging in the values, we have:
\(3^2 = 2^2 + b^2\\9 = 4 + b^2\\b^2 = 9 - 4\\b^2 = 5\)
Now we have all the necessary values to write the equation of the hyperbola. Since the foci lie on the x-axis and the center is at the origin, the equation of the hyperbola in standard form is:
\((x^2 / a^2) - (y^2 / b^2) = 1\)
Plugging in the values for a and b, we get:
\((x^2 / 2^2) - (y^2 / 5) = 1\\(x^2 / 4) - (y^2 / 5) = 1\)
Therefore, the equation of the hyperbola with foci at (±3,0) and vertices at (±2,0) is\((x^2 / 4) - (y^2 / 5) = 1\).
for such more question on hyperbola
https://brainly.com/question/16454195
#SPJ8
I just need to quickly know if my answers are correct thank you!

Answers
1) All of these questions are about evaluating those functions for each input.
9) So, let's check them out evaluating each one.
\(\begin{gathered} f(4)\Rightarrow f(x)=(\frac{1}{2}x)+13 \\ f(4)=(\frac{1}{2}\cdot4)+13 \\ f(4)=2+13\Rightarrow f(4)=15 \\ D \end{gathered}\)10)
\(\begin{gathered} f(x)=\frac{3}{5}x-10 \\ f(5)=\frac{3}{5}(5)-10 \\ f(5)=3-10 \\ f(5)=-7 \end{gathered}\)11)
\(\begin{gathered} f(x)=x^2+7 \\ f(-1)=(-1)^2+7\Rightarrow f(-1)=1+7\Rightarrow f(-1)=8 \end{gathered}\)12)
\(\begin{gathered} f(x)=3x^3-12x^2 \\ f(2)=3(2)^3-12(2)^2 \\ f(2)=24-48 \\ f(2)=-24 \end{gathered}\)What is the area enclosed by the curves???

Answers
i think

Simplify the expression
9v^2(u^2+ uv -5v^2)
Answers
Answer:
9u^2v^2+9uv^3-45v^4
plz give brainliest
Step-by-step explanation:
You invest $75 in a savings account that pays 2% annual interest. If you make no additional deposits or withdrawals, how many years will it take for the account to grow to at least $100?
A. 12 years
B. 10 years
C. 15 years
D. 17 years
Hurry please i need help
Answers
First, you would do 75 • .02 to figure out what 2% of 75 is, which it is 1.5.
Then, you divide 25 by 1.5, and get 16.66; which you would round to 17.
Hope this helps !
The time taken to amount to be $100 is approx. 17 years.
Option D is correct.
Simple interest:It is given that, principal amount is $75 and rate of interest is 2%.
Let us consider that, time taken to become amount $100 is t years.
Interest = 100 - 75 = $25
As we know that,
Interest = (P*r*t)/100
Where P is principal, r is rate and t is time.
\(25=\frac{75*2*t}{100} \\\\t=\frac{2500}{150}=16.67\)
Therefore, time taken to amount to be $100 is approx. 17 years.
Learn more about the interest here:
https://brainly.com/question/25793394
( I WILL BE GIVING EXTRA POINTS AND BRAINLIEST TO WHO EVER HELPS ME!! :D)
A recipe needs two and one sixth cups of walnuts and eight and one eighth cups of peanuts. How many cups of nuts are needed for the recipe in all?
A) ten and two fourteenths cups
B) ten and fourteen forty eighths cups
C) eleven and fourteen forty eighths cups
D) eleven and two fourteenths cups
(Here is an image if needed) :

Answers
Answer:
B I think
Step-by-step explanation:
Eight eighths in one cup. Took that and multiplied that and added the single eighth. Six sixths in one cup. Took that and multiplied that and added the single sixth again. Added the total up and got 10.2916666667. Rounded. Hope this helps!
Answer:
b
Step-by-step explanation:
You deposit $5000 in an account earning 5% interest compounded continuously. How much will you have in the account in 5 years? Round to the nearest cent.
Answers
(12sin(pi/2x)*lnx)/((x³+5)(x-1))
lim as x approaches 1
Answers
The limit of the given function as x approaches 1 is 0.
To find the limit of the given function as x approaches 1, we need to evaluate the expression by substituting x = 1. Let's break it down step by step:
1. Begin by substituting x = 1 into the numerator:
\(\[12\sin\left(\frac{\pi}{2}\cdot 1\right)\ln(1) = 12\sin\left(\frac{\pi}{2}\right)\ln(1) = 12(1)\cdot 0 = 0\]\)
2. Now, substitute x = 1 into the denominator:
(1³ + 5)(1 - 1) = 6(0) = 0
3. Finally, divide the numerator by the denominator:
0/0
The result is an indeterminate form of 0/0, which means further analysis is required to determine the limit. To evaluate this limit, we can apply L'Hôpital's rule, which states that if we have an indeterminate form 0/0, we can take the derivative of the numerator and denominator and then evaluate the limit again. Applying L'Hôpital's rule:
4. Take the derivative of the numerator:
\(\[\frac{d}{dx}\left(12\sin\left(\frac{\pi}{2}x\right)\ln(x)\right) = 12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{x} + \frac{\sin\left(\frac{\pi}{2}x\right)\ln(x)}{x}\right)\]\)
5. Take the derivative of the denominator:
\(\[\frac{d}{dx}\left((x^3 + 5)(x - 1)\right) = \frac{d}{dx}\left(x^4 - x^3 + 5x - 5\right) = 4x^3 - 3x^2 + 5\]\)
6. Substitute x = 1 into the derivatives:
Numerator: \(\[12\left(\cos\left(\frac{\pi}{2}\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{1} + \sin\left(\frac{\pi}{2}\right) \cdot \frac{\ln(1)}{1}\right) = 0\]\)
Denominator: 4(1)³ - 3(1)² + 5 = 4 - 3 + 5 = 6
7. Now, reevaluate the limit using the derivatives:
lim as x approaches 1 of \(\[\frac{{12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{{-1}}{{x}} + \sin\left(\frac{\pi}{2}x\right) \cdot \frac{{\ln(x)}}{{x}}\right)}}{{4x^3 - 3x^2 + 5}}\]\)
= 0 / 6
= 0
Therefore, the limit of the given function as x approaches 1 is 0.
For more such questions on L'Hôpital's rule
https://brainly.com/question/24116045
#SPJ8
How many cards does each friend have? See image below

Answers
Marlene earned $178 at her summer job. She already had savings of $98.25. She buys a T-shirt for $19.50. How much money does she have left?
Answers
Answer:
$256.75
Step-by-step explanation:
$178 + $98.25 = $276.25
$276.75 - $19.50 = $256.75
- The area of a rectangle can be found by using A
24w + w2, where w represents the
width. What is the width of the rectangle when the area is 3456 in.2 ?
Answers
Answer:
26w
Step-by-step explanation:
X3-x-9=0 bisection method
Answers
Step-by-step explanation:
The bisection method is a root-finding algorithm that repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. To apply the bisection method to the equation x^3 - x - 9 = 0, you need to find two initial values a and b such that f(a) and f(b) have opposite signs. This means that there is at least one root of the equation in the interval [a, b].
Let’s take a = 2 and b = 3 as our initial interval. We can see that f(2) = 2^3 - 2 - 9 = -1 and f(3) = 3^3 - 3 - 9 = 18, so f(a) and f(b) have opposite signs.
Now we can apply the bisection method as follows:
Calculate the midpoint c = (a + b)/2 = (2 + 3)/2 = 2.5.
Evaluate f© = 2.5^3 - 2.5 - 9 ≈ 5.625.
Since f© > 0 and f(a) < 0, there must be a root in the interval [a, c]. So we set b = c and repeat the process.
Calculate the new midpoint c = (a + b)/2 = (2 + 2.5)/2 = 2.25.
Evaluate f© ≈ 1.765625.
Since f© > 0 and f(a) < 0, there must be a root in the interval [a, c]. So we set b = c and repeat the process.
We can continue this process until we reach the desired level of accuracy.
The basic rate pay is K8.20. If the overtime is paid at time-and-a-quarter, what is the overtime rate of pay?
Answers
The overtime rate of pay is K10.25.
The overtime rate of pay can be calculated by multiplying the basic rate pay by the time-and-a-quarter factor. In this case, the basic rate pay is K8.20.
To determine the overtime rate of pay, we need to calculate one-quarter (1/4) of the basic rate pay, and then add that amount to the basic rate pay. One-quarter of K8.20 is calculated as (1/4) * K8.20 = K2.05.
By adding the calculated overtime amount to the basic rate pay, we get the overtime rate of pay: K8.20 + K2.05 = K10.25.
Therefore, the overtime rate of pay is K10.25.
For more such questions on pay,click on
https://brainly.com/question/25793394
#SPJ8
I’ll give brainliest! Please help

Answers
Answer:
65
Step-by-step explanation:
The lines are parallell so m1 = m5, and m3=m8. 180-115 is 65
Please help asap with this question!! :)

Answers
Answer:
Step-by-step explanation:
3x + 9x +12 = 180 {linear pairr}
12x + 12 =180
12x = 180 - 12
12x = 168
x = 168/12
x = 14
3x = 3*14 = 42
4y - 10 + 3x = 180 {linear pair}
4y - 10 + 42 = 180
4y + 32 =180
4y = 180 - 32
4y = 148
y = 148/4
y = 37
Answer:
x = 14, y = 37
Step-by-step explanation:
The angle vertically opposite (4y-10) is also a corresponding angle to (9x + 12) so that means that angles (4y-10) and (9x+12) are equal.
4y-10 = 9x+12 -----Equation 1
You also know that (4y-10) and 3x add up to 180° since they both lie on a straight line.
4y-10+3x = 180 -----Equation 2
From the above equation, I'm going to isolate (4y-10) so that I know a value that I can substitute in Equation 1.
4y-10 = 180-3x -----Equation 3
Substitute 4y-10 = 180-3x into Equation 1.
4y-10 = 9x+12
180-3x = 9x+12
Put the like terms together.
180-12 = 9x+3x
Evaluate.
12x = 168
Find x.
x = 168 ÷ 12
x = 14
Subsitite x = 14 into Equation 3.
4y-10 = 180-3x
= 180-3(14)
= 180-42
= 138
Isolate 4y.
4y = 138+10
= 148
Find y.
y = 148 ÷ 4
y = 37
En el cine, el precio de admisión de un niño es de 6 dólares y de un adulto es de 9,20 dólares . El sábado se vendieron 146 boletos de admisión para un total de ventas de 1135,20 dólares . ¿Cuántos boletos de admisión de niños se vendieron ese día?
Answers
Answer:
65 boletos.
Step-by-step explanation:
Antes de resolverSabemos que el precio para un niño es 6 dólares, y el precio para un adulto es 9,20 dólares. Además, el cine se vendió 146 boletos, y recibió 1135,20 dólares.
El procesoVamos a resolver este problema con un sistema, usando 2 varibles.
No sabemos cuantos boletos de niño el cine vendió, entonces el cine vendió <<x>> boletos de niños. Tampoco sabemos cuantos boletos de adultos vendió, entonces vendió <<y>> boletos de adultos.
En total, vendió 146 boletos; el número de los boletos de niños con el número de los boletos de adultos es 146 boletos.
Usando las variables, x + y = 146 boletos.
Esta es una de las equaciones que necesitamos.
Porque todos los boletos de niños es 6 dólares, si el cine vendió <<x>> boletos, su total de ventas (de boletos de niños) es <<6x>> dólares.
Lo mismo es verdad para los boletos de adultos; todos los boletos de adultos es 9,20 dólares, entonces si vendió <<y>> boletos, el total de ventas de boletos de adultos es <<9,20y>> dólares.
En total, las ventas de los boletos de niños + las ventas de los boletos de adultos es 1135,20 dólares.
O, con variables, es 6x + 9,20y = 1135,20
Nuestra sistema es:
x + y = 146
6x + 9,20y = 1135,20
Ahora necesitamos resolver esta sistema.
Podemos usar la sustitución. Vamos a resolver una de las eqaciones para una variable, y después, usar el valor de esa variable para encontrar la solución para una de las variables, y después, usar esa solución para encontrar la solución de la otra variable.
Podemos mover <<y>> al otro lado.
x + y = 146 => x = 146 - y
Ahora, podemos sustituir <<x>> para 146 - y en 6x + 9,20y = 1135,20
6(146-y) + 9,20y = 1135,20
Multiplica.
876 - 6y + 9,20y = 1135,20
Combina los términos que son los mismos.
876 + 3,20y = 1135,20
Mueva 876 al otro lado.
876 + 3,20y = 1135,20 => 3,20y = 259,20
Divide todo por 3,20.
3,20y/ 3,20 = 259,20/ 3,20
y = 81
Entonces, el cine vendió 81 boletos de adultos.
La respuestaRecuerda, esta (81 boletos de adultos) no es lo que necesitamos. Necesitamos cuantos boletos de niños vendió.
Entonces, podemos substituir <<y>> con 81 en x = 146 - y. Recuerda que <<x>> es cuantos boletos de niños vendió.
x = 146 - y => x = 146 - 81 => 65
Entonces, el cine vendió 65 boletos de niños.
For each random variable defined here, describe the set of possible values for the variable, and state whether the variable is discrete. X = the number of unbroken eggs in a randomly chosen standard egg carton Y = 5 the number of students on a class list for a partic- ular course who are absent on the first day of classes U = 5 the number of times a duffer has to swing at a golf ball before hitting it X = 5 the length of a randomly selected rattlesnake Z = 5 the sales tax percentage for a randomly selected amazon.com purchase Y = 5 the pH of a randomly chosen soil sample X = 5 the tension (psi) at which a randomly selected tennis racket has been strung X = 5 the total number of times three tennis players must spin their rackets to obtain something other than UUU or DDD (to determine which two play next)
Answers
In the order provided in the question, X is a discrete random variable, Y is not a random variable, U is a discrete random variable, X is a continuous random variable, Z is a continuous random variable, Y is a continuous random variable, X is a continuous random variable, and X is a discrete random variable.
• X = the number of unbroken eggs in a randomly chosen standard egg carton The possible values for X are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, or 12, as an egg carton can have anywhere between 0 and 12 unbroken eggs. X is a discrete random variable since it takes on a finite number of possible values.
• Y = 5 the number of students on a class list for a particular course who are absent on the first day of classes The only possible value for Y is 5, so it is not a random variable.
• U = 5 the number of times a duffer has to swing at a golf ball before hitting it The possible values for U are all positive integers starting from 5. U is a discrete random variable since it takes on a countable number of possible values.
• X = 5 the length of a randomly selected rattlesnake. The possible values for X are all positive real numbers. X is a continuous random variable since it can take on any value within a range of values.
• Z = 5 the sales tax percentage for a randomly selected amazon.com purchase The possible values for Z are all percentages between 0% and 100%, including decimal values. Z is a continuous random variable since it can take on any value within a range of values.
• Y = 5 the pH of a randomly chosen soil sample. The possible values for Y are all positive real numbers. Y is a continuous random variable since it can take on any value within a range of values.
• X = 5 the tension (psi) at which a randomly selected tennis racket has been strung. The possible values for X are all positive real numbers. X is a continuous random variable since it can take on any value within a range of values.
• X = 5 the total number of times three tennis players must spin their rackets to obtain something other than UUU or DDD (to determine which two play next) The possible values for X are 1, 2, 3, and so on, since the players can keep spinning the rackets indefinitely. X is a discrete random variable since it takes on a countable number of possible values.
Learn more about continuous random variable here brainly.com/question/17238189
#SPJ4
whats the perimeter of this shape??

Answers
The perimeter of the shape is 10 inches.
How to calculate the perimeter?It's important to note that the perimeter of a shape or calculated by adding all the sides together.
In this case, this is a rectangle and the perimeter will be:
Perimeter = 2(length + width)
Length = 4 inches
Width = 1 inch
Perimeter = 2(length + width)
Perimeter = 2(4 + 1)
Perimeter = 10 inches.
Learn more about perimeter on:
brainly.com/question/19819849
#SPJ1
Trigonometry: Measure tal Excel In Opt. Mathematics - Book 9 ) If the number of degrees of a certain angle added to the number of gra same angle is 152, find the angle in degrees.
Answers
The angle in degrees is 873.1843.
Let the measure of the angle be θ in degrees. Therefore, the measure of the same angle in gradians is (θ × π/180).
According to the given information, the number of degrees of a certain angle added to the number of gradians of the same angle is 152.(θ) + (θ × π/180) = 152.
Simplifying the above equation, we get:(θ) + (θ/180 × π) = 152.
Multiplying both sides of the equation by 180/π, we get:
θ + θ = (152 × 180)/π2θ = (152 × 180)/πθ = (152 × 180)/(3.14)θ = 873.1843
Thus, the angle in degrees is 873.1843.
For more such questions on angle, click on:
https://brainly.com/question/25770607
#SPJ8
A survey showed that, in one city, 20.7% of the population used
product X, 50% use product Y and among users Y, 36.5% use X. Randomized interview
However, a resident in that city, calculate the probability that that person
a) Use both X and Y;
b) Neither X nor Y
Answers
Answer:
Step-by-step explanation:
a) 0.5*0.365=18.25%
b) (100%-20,7%-50%)=29.3
Which smallest number is subtracted from the number 12675 to make it a perfect square?