Parallelogram be is a scaled copy of parallelogram U what is the value of w ( please answer ASAP I'm in a rush)

Answers
A scaled-down version of parallelogram is parallelogram be. What does w equal for U
X has a value of 4.
Line BC and line AD are parallel in the picture that was submitted, and segment 15 is the midpoint.
The Midsegment TrapezoidTheorem states that a line going through the midpoint of a trapezoid leg, parallel to both bases, will also go through the midpoint of the other leg
The formula for calculating a trapezoid's midsegment is as follows:
As a result, x has a value of 4.
A trapezoid is a quadrilateral with one pair of opposite sides parallel. It can have right angles (a right trapezoid), and it can have congruent sides (isosceles), but those are not required.
To learn more about trapezoid,
Visit : https://brainly.com/question/20374834
#SPJ9

Related Questions
What is the solution set of {x|x 5
Answers
Answer:
5x
Step-by-step explanation:
Find the area of the shape. Either enter an exact answer in terms of pi or use 3.14 for pi and enter your answer as a decimal.

Answers
Answer:
Area = 3π.
Step-by-step explanation:
This is 3/4 of a circle whose area is 3/4πr^2
= 3/4 * 2^2 * π
= = 3/4 * 4 * π
= 3π
What is 241m as a fraction of 5.4km
Answers
Answer:
i think 223/499
Step-by-step explanation:
NOWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW

Answers
Answer: X=147
Step-by-step explanation:
33+114= 147
two angles added together equals x
x=147
180-147=33
X=147°
Use a calculator to work out
2.45x107 x 4.76×10¹2
8.06×103
Give your answer in standard form to 3
significant figures.
Answers
Answer: 1.247834e+15
Step-by-step explanation: Used Calculator
find the diameter d(c d) of the opening 20cm from the vertex
Answers
The diameter d(c d) of the opening 20cm from the vertex is approximately 16.33cm.
To find the diameter of the opening 20cm from the vertex, we can use the fact that the cross-section of a cone is a circle. We can also use the formula for the slant height of a cone, which is given by the equation:
s = sqrt(r^2 + h^2)
where s is the slant height, r is the radius of the circular base, and h is the height of the cone.
In this case, we know that the height of the cone is 20cm from the vertex. We also know that the radius of the circular base is d/2, where d is the diameter we are trying to find.
So, using the formula for the slant height, we can write:
s = sqrt((d/2)^2 + 20^2)
We also know that the slant height of the cone is equal to the distance from the vertex to any point on the circumference of the base. Therefore, we can write:
s = r
where r is the radius of the circle formed by the cross-section of the cone at a height of 20cm from the vertex.
Now, equating the expressions for s and r, we get:
sqrt((d/2)^2 + 20^2) = d/2
Squaring both sides and simplifying, we get:
d^2 - 4d - 800 = 0
Using the quadratic formula, we can solve for d and get:
d = (4 + sqrt(4^2 + 4*800))/2
d = 4 + sqrt(3204))/2
d ≈ 16.33
Therefore, the long answer to your question is that the diameter of the opening 20cm from the vertex is approximately 16.33cm.
To know more about diameter visit:
https://brainly.com/question/5501950
#SPJ11
Use the procedures developed in this chapter to find the general solution of the differential equation. 3x3y''' + 28x2y'' + 55xy' + 9y = 0
Answers
Substitute \(x=e^t\). By the chain rule,
\(\dfrac{dy}{dx} = \dfrac{dy}{dt}\cdot\dfrac{dt}{dx}\)
Now \(t=\ln(x)\implies\frac{dt}{dx}=\frac1x\), so
\(\dfrac{dy}{dx} = \dfrac1x \dfrac{dy}{dt} \\\\ ~~~~~~~~ \iff \dfrac{dy}{dt} = x\dfrac{dy}{dx}\)
Differentiate both sides again to recover the second and third derivatives.
\(\dfrac{d^2y}{dx^2} = -\dfrac1{x^2}\dfrac{dy}{dt} + \dfrac1x \dfrac{d\frac{dy}{dt}}{dx} \\\\ ~~~~~~~~ = -\dfrac1{x^2}\dfrac{dy}{dt} + \dfrac1x \left(\dfrac{d\frac{dy}{dt}}{dt}\cdot\dfrac{dt}{dx}\right) \\\\ ~~~~~~~~ = -\dfrac1{x^2} \dfrac{dy}{dt} + \dfrac1{x^2}\dfrac{d^2y}{dt^2} \\\\ ~~~~~~~~ \iff \dfrac{d^2y}{dt^2} - \dfrac{dy}{dt} = x^2 \dfrac{d^2y}{dx^2}\)
\(\dfrac{d^3y}{dx^3} = \dfrac2{x^3}\dfrac{dy}{dt} - \dfrac1{x^2}\dfrac{d\frac{dy}{dt}}{dx} - \dfrac2{x^3} \dfrac{d^2y}{dt^2} + \dfrac1{x^2}\dfrac{d\frac{d^2y}{dt^2}}{dx} \\\\ ~~~~~~~~ = \dfrac2{x^3} \dfrac{dy}{dt} - \dfrac1{x^2}\left(\dfrac{d\frac{dy}{dt}}{dt}\cdot\dfrac{dt}{dx}\right) - \dfrac2{x^3} \dfrac{d^2y}{dt^2} + \dfrac1{x^2}\left(\dfrac{d\frac{d^2y}{dt^2}}{dt}\cdot\dfrac{dt}{dx}\right) \\\\ ~~~~~~~~ = \dfrac2{x^3} \dfrac{dy}{dt} - \dfrac1{x^3} \dfrac{d^2y}{dt^2} - \dfrac2{x^3} \dfrac{d^2y}{dt^2} + \dfrac1{x^3}\dfrac{d^3y}{dt^3} \\\\ ~~~~~~~~ \iff \dfrac{d^3y}{dt^2} - 3 \dfrac{d^2y}{dt^2} + 2 \dfrac{dy}{dt} = x^3 \dfrac{d^3y}{dx^3}\)
The ODE then transforms to a linear one,
\(3\left(\dfrac{d^3y}{dt^2} - 3 \dfrac{d^2y}{dt^2} + 2 \dfrac{dy}{dt}\right) + 28\left(\dfrac{d^2y}{dt^2} - \dfrac{dy}{dt}\right) + 55\dfrac{dy}{dt} + 9 y = 0\)
or using Lagrange's prime notation,
\(3(y''' - 3y'' + 2y') + 28(y'' - y') + 55y' + 9y = 0\)
\(3y''' + 19y'' + 33y' + 9y = 0\)
The characteristic equation is
\(3r^3 + 19r^2 + 33r + 9r = (r + 3)^2 \left(r + \dfrac13\right) = 0\)
with roots at \(r=-3\) and \(r=-\frac13\), so the general solution is
\(y(t) = C_1 e^{-1/3\,t} + C_2 e^{-3t} + C_3 t e^{-3t}\)
Back in terms of \(x\), we get
\(\boxed{y(x) = C_1 x^{-1/3} + C_2 x^{-3} + C_3 x^{-3}\ln(x)}\)
pls help i dont understand

Answers
Answer:
D and C should be correct.
Step-by-step explanation:
What is the longest increasing subsequence problem in dynamic programming?
Answers
The Longest Increasing Subsequence (LIS) problem is a classic problem in dynamic programming. Given a sequence of numbers, the problem is to find the longest subsequence in which the numbers are in increasing order. For example, given the sequence {3, 1, 5, 2, 4}, the longest increasing subsequence is {1, 2, 4}, which has length 3.
The LIS problem can be solved using dynamic programming by defining an array to store the length of the longest increasing subsequence that ends at each position in the sequence. The array is initialized to 1, and then for each position i in the sequence, the length of the longest increasing subsequence that ends at i is calculated by finding the maximum length of any subsequence that ends at a position j < i and has a smaller value than the value at i. The final solution is the maximum length of any subsequence in the array.
Find out more about dynamic programming
brainly.com/question/29809157
#SPJ4
7.) The online book is $29.00 but the tax and shipping is another 25%. What will it cost me with the tax and shipping?
Answers
Answer:
$36.25
Step-by-step explanation:
Shipping and tax are 25% the price of online book, thus it will be 25/100 x 29 = $7.25
Thus, total will be 29 + 7.25 = $36.25
This sketch represents Terry on horizontal ground, flying a kite K. an imaginary right
angled triangle TKZ can be drawn. The string TK is 18.2m long and makes an angle of
72 with the horizontal TZ.
Work out the value of
Answers
The measure of <TKZ is 18 degree.
The length of KZ is 17.3082 m.
The height of the kite K from the ground is 18.3082 m.
We have,
Angle of Elevation = 72
TK = 18.2 m
Using trigonometry
sin 72 = P/ H
sin 72 = P / 18.2
P = 17.3082
Now, cos 72 = B/H
cos 72 = B/ 18.2
B = 5.6238
Now, <TKZ = 180 - 90 - 72 (angle Sum property)
<TKZ = 18 degree
and, length of KZ = 17.3082 m
Not, the height of the kite K from the ground
= 18.3082 m
Learn more about Trigonometry here:
https://brainly.com/question/11016599
#SPJ1
A bakery offers a sale price of $3.30 for 3 muffins. what is the price per dozen?
Answers
Answer:
$13.20
Step-by-step explanation:
A dozen consists of 12 items. If you have 3 you must multiply the current amount by 4 to get 12. Therefore you must also multiply the price by 4.
3.30*4=13.20
When using the rational root theorem which of the following is a possible root function below

Answers
The possible rational roots are
\(=\frac{\text{factors of the constant}}{\text{factors of the lead coefficient}}\)The constant is 14, and its factors are:
\(\pm1,\pm2,\pm7,\pm14\)The lead coefficient is 1, and its factors are:
\(\pm1\)Then, the possible rational roots for this equation are
\(\frac{\pm1,\pm2,\pm7,\pm14}{\pm1}=\pm1,\pm2,\pm7,\pm14\)Since, 7 is a possible rational root, the answer is option C
Which expression is the opposite of 2(3x -8)?
Answers
The opposite of 2(3x-8) is 1/(6x-16)
What is inverse of an expression?The inverse of an expression is thesame as the opposite of an expression.
Inverse operations are pairs of mathematical manipulations in which one operation undo the action of the other. The inverse of a number usually means its reciprocal.The product of a number and its inverse will be equal to 1.
For example the reciprocal of 5 is 1/5. That is 5×1/5= 1
Also the inverse of a fraction like 5/7 is 7/5. That is 5/7× 7/5 = 1
Similarly, the inverse of 2(3x-8) will be 1/2(3x-8)
= 1/6x- 16.
Therefore the inverse of 2(3x-8) = 1/(6x-16)
learn more about inverse of expression from
https://brainly.com/question/3831584
#SPJ1
find a power series representation for the function and determine the interval of convergence. (give your power series representation centered at x = 0.) f(x)=1/(6 x)
Answers
The power series representation of f(x) is f(x) = (1/6) * (1 - x/6 + x²/36 - x³/216 + ...) and centered at x = 0. Also, the interval of convergence for the power series representation.
Understanding Power SeriesThe function f(x) = 1/(6x) can be represented as a power series using the geometric series formula. Recall that the geometric series formula is:
1 / (1 - r) = 1 + r + r² + r³ + ...
In this case, we can rewrite f(x) as:
f(x) = 1/(6x) = (1/6) * (1/x) = (1/6) * (1/(1 - (-x/6)))
Now, we can identify that the function is in the form of a geometric series with a common ratio of -x/6. Therefore, we can use the geometric series formula to write f(x) as a power series:
f(x) = (1/6) * (1/(1 - (-x/6)))
= (1/6) * (1 + (-x/6) + (-x/6)² + (-x/6)³ + ...)
Simplifying the expression:
f(x) = (1/6) * (1 - x/6 + x²/36 - x³/216 + ...)
This is the power series representation of f(x) centered at x = 0.
To determine the interval of convergence, we need to find the values of x for which the power series converges. In this case, the power series is a geometric series, and we know that a geometric series converges when the absolute value of the common ratio is less than 1.
In our power series, the common ratio is -x/6. So, for convergence, we have:
|-x/6| < 1
Taking the absolute value of both sides:
|x/6| < 1
-1 < x/6 < 1
-6 < x < 6
Therefore, the interval of convergence for the power series representation of f(x) is -6 < x < 6.
Learn more about power series here:
https://brainly.com/question/28158010
#SPJ1
Omar models a can of ground coffee as a right cylinder. He measures its height as 5 3/4 in. in and its circumference as 5 in. Find the volume of the can in cubic inches. Round your answer to the nearest tenth if necessary.
Answers
Answer:
28.75 inches
Step-by-step explanation:
1.) 5 3/4 x 5/1 = 28 3/4
2.) 28 3/4 simplified is 28.75
Hope that helps!
To prove that △vwz ~ △yxz by the sas similarity theorem, which other sides or angles should be used? wv and xy wv and zy ∠vzw ≅ ∠yzx ∠vwz ≅ ∠yxz
Answers
In order to prove that △VWZ ~ △YXZ by SAS theorem we must have ∠VZW ≅ ∠YZX. Thus, option c is the most appropriate choice.
To prove that △VWZ ~ △YXZ by SAS theorem, we must prove that two sides of each triangle such that the angle between these sides is congruent are also congruent.
now △VWZ ~ △YXZ is to be proved, it implies that -
∠V ↔︎ ∠Y
∠W ↔︎ ∠X
∠Z ↔︎ ∠Z
thus ∠VZW ≅ ∠YZX should be true.
hence, option c is correct and that automatically strikes out option d.
now the sides involving Z should also be congruent to prove that
△VWZ ~ △YXZ
thus, side WZ ≅ side XZ and side VZ ≅ side YZ
since we don't have such an option- options a and b are not the correct choices for this question.
Read more about the SAS test:
brainly.com/question/14252518
#SPJ4
The complete question is -
In the diagram, VZ/YZ=WZ/XZ
To prove that VWZ~YXZ by the SAS similarity theorem, Which other sides or angles should be used?
a. WV and XY
b. WV and YZ
c. ∠VZW ≅ ∠YZX
d. ∠VWZ ≅ ∠YXZ
Which values are within the range of the piecewise-defined function?
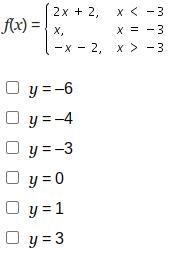
Answers
The values within the range of the piecewise-defined function are
y = -6, y = -4, y = 1 and y = 3.
What is a piecewise function?A piecewise function, or f(x), is a function with various definitions at various intervals of x. A piecewise function's graph is divided into sections that each correspond to one of its definitions. A very good illustration of a piecewise function is the absolute value function.
Given f(x) = 2x + 3, if x < -3
f(x) = x, if x = -3
f(x) = -x - 2, if x > -3
the function will be at x ≤ -3 and x ≥ -3
We now wish to determine which values fall within this function's range. Keep in mind that the set of possible outputs from a function constitutes its range.
The range of the first part of the function f(x) = 2*x + 2 has an upper bound at x = -3
f(-3) = 2*-3 + 2 = -6 + 2 = -4
Then the range of the first part is (-∞, -4)
Notice that the actual value -4 belongs to the range because x is smaller than and equal to -3.
The range of the second part has a lower bound for x = -3, the lower bound is:
f(-3) = -(-3) - 2 = 1
Then the range of this part is (1, ∞)
Then the range of the piecewise function is:
(-∞, -4) U (1, ∞)
and including -4 and 1
y = -6, y = -4
y = 1, y = 1
Hence values in the range are y = -6, y = -4, y = 1, and y = 3.
Learn more about piecewise function;
https://brainly.com/question/12561612
#SPJ1
F(x)=4x^2+3x+13
Find f(1)
Answers
Answer:
f(1) = 42
Step-by-step explanation:
Step 1: Switch all x out to 1 for f(1) which would look like this: f(1)=4(1)^2+3(1)+13
Step 2: You would then simplify it starting with 4(1)^2 which would equal 4 squared which equals 16.
Step 3: After simplifying you would have f(1)=16+3+13
Step 4: You then just add and get 42
Hope this helped :D
Simplify |-5 - 3| + (-8)
-10
-16
0
Answers
Answer:
The correct answer is option C.
Step-by-step explanation:
1) Simplify -5 - 3 to -8.
\( | - 8| - 8\)
2) Simplify | -8 | - 8 to 8.
\(8 - 8\)
3) Simplify.
\(0\)
Therefor, the answer is Option C. 0.
Answer:
0
Step-by-step explanation:
|-5 - 3| + (-8)
First simplify the absolute value
|-5 - 3| = |-8| and absolute value is positive so 8
8 + (-8) =0
persevere of all the students at north high school, 25% are enrolled in algebra and 20% are enrolled in algebra and health. a. if a student is enrolled in algebra, find the probability that the student is enrolled in health as well. p(algebra)
Answers
The probability that a student enrolled in algebra is also enrolled in health is 0.8.
Let's denote the event of a student being enrolled in algebra as A and the event of a student being enrolled in health as H. We are given that 25% of the students are enrolled in algebra (P(A) = 0.25) and 20% of the students are enrolled in both algebra and health (P(A ∩ H) = 0.20).
We want to find P(H|A), the probability that a student is enrolled in health given that the student is enrolled in algebra.
Using the conditional probability formula:
P(H|A) = P(A ∩ H) / P(A)
We substitute the given values:
P(H|A) = 0.20 / 0.25
Simplifying this expression:
P(H|A) = 0.80
Therefore, the probability that a student enrolled in algebra is also enrolled in health is 0.80, or 80%.
For more questions like Probability click the link below:
https://brainly.com/question/11234923
#SPJ11
find the coordinates of the missing endpoint if M is the midpoint of DF
F(2,9) M(-1,6)
Answers
Answer:
(-4,3)
Step-by-step explanation:
\(\frac{x+5}{x+9}+\frac{x+7}{x^{2}-9}÷\frac{x^{2}-9}{x+3}\)
Answers
The result for the division of the fractions in this problem is given as follows:
\(\frac{x^3 + 6x^2 + 7x + 18}{(x - 3)(x + 9)(x^2 - 9)}\)
How to divide two fractions?The division of two fractions is given by the multiplication of the first fraction by the inverse of the second fraction.
The first fraction in this problem is composed by the sum of two fractions, as follows:
\(\frac{x + 5}{x + 9} + \frac{x + 7}{x^2 - 9}\)
Applying the subtraction of perfect squares, we have that:
x² - 9 = (x - 3)(x + 3).
The second fraction is given as follows:
(x² - 9)/(x + 3).
Considering the factoring of x² - 9, the second fraction is given as follows:
x - 3.
Hence the inverse is of:
1/(x - 3).
Then the entire quotient is given as follows:
\(\left(\frac{x + 5}{x + 9} + \frac{x + 7}{x^2 - 9}\right) \times \frac{1}{x - 3}\)
The addition of the two fractions is given as follows:
\(\frac{(x + 5)(x^2 - 9) + (x + 7)(x + 9)}{(x + 9)(x^2 - 9)} = \frac{x^3 + 6x^2 + 7x + 18}{(x + 9)(x^2 - 9)}\)
Applying the multiplication by x - 3 in the denominator, the quotient is given as follows:
\(\frac{x^3 + 6x^2 + 7x + 18}{(x - 3)(x + 9)(x^2 - 9)}\)
Missing InformationThe problem asks for the quotient between the two fractions.
More can be learned about division of fractions at https://brainly.com/question/1622425
#SPJ1
It’s all due at midnight please help

Answers
The functions g and h, have values for the inverse functions g⁻¹(9) = 1 and h⁻¹(-1) = -1. The composite function (h o h⁻¹)(-1) is equal to -1.
What is Inverse of a functionA function is said to have an inverse if it is both one-to-one and onto
for the function g using y = mx + c, when x = 1 and y = 9
m = 8/5 and c = 37/5
g(x) = (8/5)x + 37/5
g⁻¹(x) = (5x - 37)/8
g⁻¹(9) = [5(9) - 37]/8
g⁻¹(9) = (45 - 37)/8
g⁻¹(9) = 8/8
g⁻¹(9) = 1
for the function h(x) = -3x - 4, the inverse;
h⁻¹(x) = -(x + 4)/3
h⁻¹(-1) = -(-1 + 4)/3
h⁻¹(-1) = -3/3 = -1
(h o h⁻¹)(-1) = -[3(-1)] - 4
(h o h⁻¹)(-1) = -(-3) - 4
(h o h⁻¹)(-1) = 3 - 4
(h o h⁻¹)(-1) = -1.
Therefore, for the functions g and h, the values for the inverse functions g⁻¹(9) = 1 and h⁻¹(-1) = -1. The composite function (h o h⁻¹)(-1) is equal to -1.
Know more about function here:https://brainly.com/question/14391067
#SPJ1
how many ways are there to put $4$ balls into $3$ boxes, given that the balls are not distinguished and neither are the boxes?
Answers
Answer:
Step-by-step explanation:
think that there are 15 ways ... call the boxes A, B, and C.
You could put all four b***s into either box A, or box B, or box C ---> 3 ways.
You could put three ball into one box and the other ball into another box:
-- 3 into A, 1 into B, 0 into C; or 3 into A, 0 into B, 1 into C; or 1 into A, 3 into B, 0 into C; or 1 into A, 0 into B, 3 into C; or 0 into A, 3 into B, 1 into C; or 0 into A, 1 into B, 3 into C ---> 6 ways
You could put two balls into one box and the other two balls into another box:
-- 2 into A, 2 into B, 0 into C; or 2 into A, 0 into B, 2 into C; or 0 into A, 2 into B, 2 into C ---> 3 ways.
You could put two b***s into one box and one ball into each of the other two boxes:
-- There are three boxes that could get the two b***s ---> 3 ways
Total: 3 + 6 + 3 + 3 = 15 ways.
plzzzzzzzz help fast im slow

Answers
Answer:
c
Step-by-step explanation:
Answer:
the first one
Step-by-step explanation:
The measure of one acute angle of a right triangle is 6 less than twice the measure of the other acute angle. Find the measure of each acute angle.
Answers
The measure of each of the acute angles of the right triangle is 32° and 58°.
A right triangle is a kind of triangle which has a right angle (90°) and two acute angles (less than 90°).
Let x = measure of one of the acute angles
If the measure of one acute angle of a right triangle is 6 less than twice the measure of the other acute angle, then
measure of the other acute angle = 2x - 6
The sum of all the angles of any triangle is equal to 180°. Hence,
90° + x + 2x - 6 = 180°
Solve for the value of x.
3x = 96
x = 32
Solve for the measure of the other acute angle.
2x - 6 = 2(32) - 6 = 58
Hence, the two angles are 32° and 58°.
Learn more about right triangles here: https://brainly.com/question/1635412
#SPJ4
Blue
A bowl contains:
• 3 red erasers
• 4 blue erasers
.6 green erasers
• 7 pink erasers
An eraser will be drawn from
the bowl and replaced 50 times.
What is a reasonable prediction
for the number of times a green
eraser will be drawn?
Answers
Answer:
i think it will be chose 3 times
Step-by-step explanation:
im not sure thats my pridiction
Answer:
0.4
Step-by-step explanation:
suppose one painter can paint the entire house in twelve hours, and the second painter takes eight hours to paint a similarly-sized house. how long would it take the two painters together to paint the house?
Answers
It would take the two painters together eight hours to paint the house
Step-by-step explanation: Given that, One painter can paint the entire house in twelve hours. The second painter takes eight hours to paint a similarly-sized house. To find, How long would it take the two painters together to paint the house? Suppose one painter takes x hours to paint the house.
Therefore, the other painter will take x-4 hours to paint the same house. According to the question, \(1/x+1/(x-4)=1/12+1/8\) Multiply by LCM, \(8(x-4)=12x+12(x-4)8x-32=6x+484x=80x=20\)Therefore, the first painter will take 20 hours to paint the house. The second painter will take 16 hours (20-4). Together they will take, \(1/20+1/16=0.1+0.0625=0.1625\) Thus, they will take 6.1538 hours which can be rounded to 4.8 hours.
See more about hours at: https://brainly.com/question/291457
#SPJ11
number of pages read by Mrs.V's class. Stem Leaf 1 24.45 23 7 7 7 8 9 314 4 69 4335 51 67 Key: 215 means 25 pages by the data in the stem and leaf plot? ess than 20 pages.
Answers
Given,
The stem and leaf plot of the data is shown in question.
The first statement is median is 30.
Here, the median of the data is 30.
Hence, statement 1 is correct.
The second statement is that the number of student who read less than 20 pages are 10.
But the number of student who reads less than 20 pages are 4.
Hence, statement 2 is also incorrect.
The third statement is over 50% of students read less than 20 pages
Here,
total number of students are 20.
The number of student who can read only pages less than 20 are 4.
4 is 20% of 20.
Hence, statement 3 is also incorrect.
The forth statement is the range of the data is 52.
Range= larger value - smaller value
= 67 - 12
= 55
Here, the range of the given data is the 55.
Hence, statement 4 is not correct.