Out of the 125 children at summer camp, 45 signed up for swimming and 38 signed up for arts and crafts. Twelve students who signed up for swimming also signed up for arts and crafts. If a child is randomly selected, what is the probability that they are signed up for swimming, if it is known that they did not sign up for arts and crafts? Please help!
Answers
Answer:33/125
Step-by-step explanation:
First, you subtract 12 from 45, because there were 45 who signed up for swimming and 12 of them also signed up for arts and crafts. So, there are 33 children, out of the 125, who only signed up for swimming. Which means there is a 33/125 chance that a child who only signed up for swimming is randomly selected.
Related Questions
The radius of a tire with the rim is 30 inches. The rim has a radius of 20 inches. What is the approximate area of the tire without the rim
Answers
The approximate area of the tire without the rim is approximately 1570 square inches.
To calculate the approximate area of the tire without the rim, we can subtract the area of the rim from the area of the entire tire.
The area of a circle is given by the formula:
\(A = \pi r^2,\)
where A represents the area and r represents the radius.
Let's calculate the area of the entire tire first:
Area of the entire tire \(= \pi (30 inches)^2\)
Next, let's calculate the area of the rim:
Area of the rim \(= \pi (20 inches)^2\)
Finally, we can subtract the area of the rim from the area of the entire tire to find the approximate area of the tire without the rim:
Approximate area of the tire without the rim = Area of the entire tire - Area of the rim
Approximate area of the tire without the rim \(= \pi (30 inches)^2 - \pi (20 inches)^2\)
Now we can calculate the approximate area:
Approximate area of the tire without the rim = π(900 square inches) - π(400 square inches)
Approximate area of the tire without the rim = π(500 square inches)
Since π is approximately equal to 3.14, we can further approximate the area:
Approximate area of the tire without the rim ≈ 3.14(500 square inches)
Approximate area of the tire without the rim ≈ 1570 square inches.
For similar question on area.
https://brainly.com/question/25292087
#SPJ11
(16+3)-10÷5×3^2? with explanation step by step
Answers
Here, we want to simplify the given expression
We shall use the order of simplification for this
The order is PEDMAS
We shall start with the terms in parentheses before we move to the exponents
We have;
\(\begin{gathered} (16+3)-10\div5\times3^2 \\ =\text{ 19-10}\div5\times3^2 \end{gathered}\)Next is the exponent
\(=\text{ 19-10}\div5\times9\)The next thing to do is to divide
\(=\text{ 19-}2\times9\)The next thing to do is to multiply
\(=\text{ 19-18}\)We then proceed to subtract;
\(=\text{ 19-18 = 1}\)The universal quantifier â (read: for all) introduces a variable and then asserts that,
for any symbol that can be bound to that variable, a following statement holds. For
example, if we wished to assert that for all apples x, x is red or green we could say:
Answers
This is a logical symbol, represented by the symbol â, which introduces a variable and asserts that any symbol that can be bound to that variable will satisfy a following statement.
In your example, the variable is "x" and the statement being asserted is "x is red or green". This means that for any apple that can be represented by the variable "x", it will either be red or green. So the statement can be written as: "âx (x is an apple -> x is red or green)" which reads as "for all apples x, x is red or green".
In order to assert that for all apples x, x is red or green using the universal quantifier, we can formulate the statement as follows:
∀x (A(x) → (R(x) ∨ G(x)))
Here's a step-by-step explanation of the statement:
1. "∀x" is the universal quantifier, which introduces the variable 'x' and asserts that the following statement holds for all possible values of 'x'.
2. "A(x)" represents the property of being an apple for the variable 'x'.
3. "R(x)" represents the property of being red for the variable 'x'.
4. "G(x)" represents the property of being green for the variable 'x'.
5. "R(x) ∨ G(x)" represents the disjunction (logical OR) of 'x' being red or green.
6. "A(x) → (R(x) ∨ G(x))" is the statement that if 'x' is an apple, then 'x' is either red or green.
So, the statement ∀x (A(x) → (R(x) ∨ G(x))) asserts that for all apples x, x is red or green.
Visit here to learn more about universal quantifier:
brainly.com/question/31518876
#SPJ11
enlarge shape q by a scale factor of -1/2 around the centre point (0,0
Answers
The new coordinates of the point in the transformed shape would be (-1/2x, -1/2y).
What is a transformation?A point is transformed when it is moved from where it was originally to a new location. Translation, rotation, reflection, and dilation are examples of different transformations.
A scale factor of -1/2 around the center point (0,0) would reflect the shape across the origin and also shrink it by a factor of 1/2.
The transformation can be represented by the matrix:
[-1/2 0]
[ 0 -1/2]
This matrix would be applied to the coordinates of each point in the shape to obtain the new coordinates of the transformed shape.
So, if a point in the shape had coordinates (x, y), the new coordinates of the point in the transformed shape would be (-1/2x, -1/2y).
To learn more about the transformations click here :
https://brainly.com/question/28029674
#SPJ1
The question seems to be incomplete the correct question would be:
Enlarge shape q by a scale factor of -1/2 around the center point (0,0). if a point in the shape had coordinates (x, y), what are the new coordinates?
billys cell phone bill is 40 dollars a month plus 50 cents for each minute he goes over
Answers
Answer:
.50x+40
Step-by-step explanation:
A water sprinkler sends water out in a circular pattern. What is the area formed by the water pattern if it can spray out 14 feet in any direction? Use 3.14 for x.
The area formed is about square feet.
(Type an integer or a decimal.)
Answers
The area formed by the water pattern of a sprinkler that can spray out 14 feet in any direction is about 615.44 square feet.
Explain the term area.
Area is the measure of the size of a two-dimensional surface or region, usually measured in square units. It is the amount of space enclosed by a flat shape or the surface of an object. The area of a shape can be calculated using formulas based on its dimensions and geometry.
According to the given information
The formula for calculating the area of a circle is A = πr² where A is the area and r is the radius of the circle. In this case, r = 14 feet and π = 3.14 so A = 3.14 x (14)² = 615.44 square feet
To know more about area visit
brainly.com/question/27683633
#SPJ1
omg please please help i really need it and i’ll give brainliest if you give a correct answer also here’s some angel numbers: 111 777 999 555

Answers
Answer:
There are 120 red marbles in the jar (last option)
Step-by-step explanation:
System of Equations
Let's call:
x = number of red marbles in the jar
y = number of blue marbles in the jar
It's given there are 320 marbles in the jar, thus:
x + y = 320
Solving for y:
y = 320 - x [1]
It's also given the ratio of blue marbles to red marbles is 5 to 3, thus:
\(\displaystyle \frac{y}{x}=\frac{5}{3}\)
Cross-multiplying:
3y = 5x [2]
Substituting [1] in [2]:
3(320 - x) = 5x
Operating:
960 - 3x = 5x
Adding 3x:
8x = 960
Dividing by 8:
x = 960/8 = 120
x = 120
There are 120 red marbles in the jar (last option)
if cos2A= -1/2 then show that cosA=1/2
Answers
Step-by-step explanation:
If cos 2A = tan-B, then show that cos 2B = tan-A.
In ABC, prove that
cos A = 1/2 (See proof below)
\(cos(2A) = 2cos^{2} A-1\)
Substitute cos 2A = -1/2 into the relationship above:
\(\frac{-1}{2} = 2cos^{2} A - 1\\\frac{-1}{2} + 1 = 2cos^{2} A\\\frac{1}{2} = 2cos^{2} A\)
Divide both sides by 2:
\(\frac{1}{4} = cos^{2} A\)
Square root both sides:
\(cosA = \sqrt{\frac{1}{4} } \\cosA = \frac{1}{2}\)
Proved
Learn more here: https://brainly.com/question/22852405
Please help mee!!! Will give brainliest!

Answers
Answer:
B.11+7=18
Step-by-step explanation:
its B because since its 7 days AFTER it means your going to have to add the 11 days plus this 7 days. Which would give you 18 days left till Susie's concert.
A rental car company charges $40 per day to rent a car and $0.08 for every mile driven. Justin wants to rent a car, knowing that:
He plans to drive 125 miles.
He has at most $170 to spend.
Write and solve an inequality which can be used to determine xx, the number of days Justin can afford to rent while staying within his budget.
Answers
The inequality we want to find is:
$40 + $0.08*x ≤ $170
Where x is the number of miles Justin can drive, and the solution is:
x ≤ 1,625
How to write the inequality?We know that there is a fixed cost of $40 plus $0.08 for every mile driven. So if you rent the car and drive for x miles, the total cost is:
C(x) = $40 + $0.08*x
We know that Justin has at most $170 to spend, so we can write the inequality:
$40 + $0.08*x ≤ $170
Solving this for x, we get:
$0.08*x ≤ $170 - $40
$0.08*x ≤ $130
x ≤ $170 /$0.08
x ≤ 1,625
So Justin can drive at most 1625 miles with the money he has.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
Answer:
Inequality: 40x+10≤170
Answer: x 4x≤4
Step-by-step explanation:
trust me
X-7/20=5/16 solve for x
Answers
x = 53/80 = 0.6625
if isn't right I have another equation
Answer:
13.25
Step-by-step explanation:
\(x - 7 \div 20 = 5 \div 16\)
by cross multiplying
16(x-7)=5(20)
16x-112=100
16x=100+112
16x=212
x=212 /16
×=13.25
if the question is this

Find a function of the form
y
=
A
sin
(
k
x
)
+
C
or
y
=
A
cos
(
k
x
)
+
C
whose graph matches this one:
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
-13
-14
1
2
3
4
5
6
7
8
9
10
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
(Leave your answer in exact form; if necessary, type pi for
π
.
y
=

Answers
Answer:
Step-by-step explanation:
The amplitude is 6, so A=6.
Also, the midline is y=-3, so C=-3.
The period is 10, so 2pi/k = 10 -> k=5.
Now we need to determine if this is a sine graph or a cosine graph. As the y-intercept is not the value of C, we can determine that this is a cosine graph, and thus y=6cos(5x)-3.
Newsweek performed a poll in which 567 American parents were asked the question, "Would you prefer to have your child taught by a male or female for grades K-2?" Only 12% responded that they would prefer to have their child taught by a male in grades K-2. Construct a 99% confidence interval for the poll.
Answers
At a 99% confidence level, the confidence interval for the proportion of American parents who prefer to have their child taught by a male teacher in grades K-2 is approximately 0.084878 to 0.155122.
To construct a confidence interval for the poll, we can use the formula for calculating the confidence interval for a proportion:
Confidence Interval = Sample proportion\(\ ^+_-\\)Margin of error
Given information:
Sample size (n) = 567
The proportion of parents preferring a male teacher (phat) = 0.12 (12%)
Confidence level = 99% (which corresponds to a z-value of approximately 2.576)
First, let's calculate the margin of error (ME):
\(= z * \sqrt{((phat * (1 - phat)) / n)}\\ = 2.576 * \sqrt{((0.12 * (1 - 0.12)) / 567)}\\ = 2.576 * \sqrt{(0.1056 / 567)}\\ = 2.576 * \sqrt{(0.0001860391)}\\ = 2.576 * 0.0136385729\\ = 0.035122 (rounded\ to\ five\ decimal\ places)\)
Now, we can calculate the confidence interval:
\(Confidence Interval = phat\ ^+_-\ ME\\Confidence Interval = 0.12\ ^+_-\ 0.035122\\Confidence Interval = (0.084878, 0.155122)\)
Therefore, at a 99% confidence level, the confidence interval for the proportion of American parents who prefer to have their child taught by a male teacher in grades K-2 is approximately 0.084878 to 0.155122.
Learn more about Confidence intervals at:
https://brainly.com/question/29576113
#SPJ4
Find the total differential of the function. \[ f(x, y)=x^{2} e^{2 y}+y \ln (x) \] \[ d f= \]
Answers
The total differential of the function \(\(f(x, y) = x^2 e^{2y} + y \ln(x)\)\) is:
\(\[df = (2x e^{2y} + \frac{y}{x})dx + (2x^2 e^{2y} + \ln(x))dy\]\)
To obtain the total differential of the function \(\(f(x, y) = x^2 e^{2y} + y \ln(x)\)\), we can compute the partial derivatives with respect to each variable and then express the total differential \(\(df\)\) as the sum of the differentials of each variable multiplied by their respective partial derivatives.
Let's calculate it step by step:
1. Calculate the partial derivative with respect to x, denoted as \(\(\frac{\partial f}{\partial x}\)\):
\(\[\frac{\partial f}{\partial x} = 2x e^{2y} + \frac{y}{x}\]\)
2. Calculate the partial derivative with respect to y, denoted as \(\(\frac{\partial f}{\partial y}\)\): \(\[\frac{\partial f}{\partial y} = 2x^2 e^{2y} + \ln(x)\]\)
3. Express the total differential \(\(df\)\) using the calculated partial derivatives:
\(\[df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy\]\)
Substituting the values of the partial derivatives we obtain the total total differential of the function \(\(f(x, y) = x^2 e^{2y} + y \ln(x)\)\) as:
\(\[df = (2x e^{2y} + \frac{y}{x})dx + (2x^2 e^{2y} + \ln(x))dy\]\)
To know more about total differential refer here:
https://brainly.com/question/33115232#
#SPJ11
Alice draws a 2-card hand from a standard 52-card deck and counts aces, while Bob rolls two dice and counts aces. The game show host randomly picks either Alice or Bob behind a curtain, tells you something about the number of aces the mystery person obtained, and asks you to guess who it is. If the host tells you the mystery person got two aces, and you guess it is Bob, what is the probability you are right?
Answers
The probability that you are right is 0%.
Alice draws a 2-card hand from a standard 52-card deck, which means there are only four aces in the deck. On the other hand, Bob rolls two dice, each with six sides, so there are only two ways to roll two aces: rolling a double 1 or rolling a double 6. These events are much less likely compared to Alice drawing two aces from the deck.
Given that the game show host tells you that the mystery person obtained two aces, the only possible explanation is that it must be Alice. Bob simply does not have a high enough probability of rolling two aces to be considered as the mystery person in this scenario.
In summary, because Bob's chances of rolling two aces are significantly lower than Alice's chances of drawing two aces, the probability of you being right by guessing Bob is 0%.
Learn more about probability
brainly.com/question/31828911
#SPJ11
Two cars travel at the same speed to different destinations. Car A reaches its destination in 12 minutes. Car B reaches its destination in 18 minutes. Car B travels 4 miles farther than Car A. How fast do the cars travel? Write your answer as a fraction in simplest form.
Answers
Answer:
chatGPT
Step-by-step explanation:
Let's denote the speed of each car as v, and the distance that Car A travels as d. Then we can set up two equations based on the information given:
d = v * (12/60) (since Car A reaches its destination in 12 minutes)
d + 4 = v * (18/60) (since Car B travels 4 miles farther than Car A and reaches its destination in 18 minutes)
Simplifying the equations by multiplying both sides by 60 (to convert the minutes to hours) and canceling out v, we get:
12v = 60d
18v = 60d + 240
Subtracting the first equation from the second, we get:
6v = 240
Therefore:
v = 240/6 = 40
So the cars travel at a speed of 40 miles per hour.
find the four second partial derivatives. observe that the second mixed partials are equal. z = x4 − 6xy 2y3.
Answers
The four second partial derivatives are:
∂²z/∂x² = 12x²
∂²z/∂y² = -24xy - 90xy⁴
∂²z/∂x∂y = -12y² - 90xy⁴
∂²z/∂y∂x = -12y² - 90xy⁴
How to find the partial derivatives?We are given the function:
z = x⁴ − 6xy²y³
The first-order partial derivatives are:
∂z/∂x = 4x³ − 6y²y³
∂z/∂y = -12xy² - 18xy⁵
Differentiating these partial derivatives with respect to x and y again:
∂²z/∂x² = ∂/∂x (4x³ − 6y²y³ ) = 12x²
∂²z/∂y² = ∂/∂y (-12xy² - 18xy⁵) = -24xy - 90xy⁴
To find the mixed partial derivatives, we differentiate the first partial derivatives with respect to the other variable:
∂²z/∂x∂y = ∂/∂x (-12xy² - 18xy⁵) = -12y² - 90xy⁴
∂²z/∂y∂x = ∂/∂y (4x³ − 6y²y³) = -12y² - 90xy⁴
As observed, the second mixed partial derivatives, ∂²z/∂x∂y and ∂²z/∂y∂x, are equal to each other: -12y² - 90xy⁴
So, the four second partial derivatives are:
∂²z/∂x² = 12x²
∂²z/∂y² = -24xy - 90xy⁴
∂²z/∂x∂y = -12y² - 90xy⁴
∂²z/∂y∂x = -12y² - 90xy⁴
Read more about Partial Derivatives at: https://brainly.com/question/31399205
#SPJ4
a company plans to manufacture a rectangular box with a square base, an open top, and a volume of 246 in.3. the cost of the material for the base is 0.2 cents per square inch, and the cost of the material for the sides is 0.3 cents per square inch. determine the dimensions of the box that will minimize the cost of manufacturing it. what is the minimum cost?
Answers
The dimensions of the box that will minimize the cost of manufacturing it: base = 9.04 in and y = 3.01 in
And the minimum cost is 32.65 cents
Let us assume that x represents the base side of the box, and y represents the height of the box.
The volume of the box would be:
V = x²y
246 = x²y ........(1)
The cost of the material for the base is 0.2 cents per square inch, and the cost of the material for the sides is 0.3 cents per square inch.
Since this box has 4 sides and 1 base, the total cost would be,
C = (0.2 × x² × 1) + (0.3 × 4 × xy)
C = 0.2x² + 1.2x(246x⁻²) (from (1) y = 246x⁻²)
C = 0.2x² + 295.2 x⁻¹
Consider derivative with respect to x,
dC/dx = 0.4x - 295.2 x⁻²
Consider dC/dx = 0
So, 0.4x - 295.2 x⁻² = 0
0.4x³ = 295.2
x³ = 738
So, x = 9.04
So, the value of y would be:
y = 246 x⁻²
y = 246 × (9.04)⁻²
y = 3.01
So, the minimum cost would be:
C = (0.2 × 0.04² × 1) + (0.3 × 4 × 9.04 × 3.01)
C = 32.65
Therefore, the minimum cost is: 32.65 cents
Learn more about the cost here:
https://brainly.com/question/19075809
#SPJ4
tim drives at an average speed of 80km per hour for 3 hours 35 minutes work out how many kilometres tim drives
Answers
Answer:
286 2/3 km
Step-by-step explanation:
Recalling that 1 hour = 60 minutes, we convert '3 hours 35 minutes' to
3 + (35/60) hours, or 3 35/60 hours, or 3.5833 hours.
Since distance = (rate)(time),
the distance driven by tim is (80 km/hr)(3.5833 hrs) = 286 2/3 km
In a survey of 400 likely voters, 214 responded that they would vote for the incumbent and 186 responded that they would vote for the challenger. Let p denote the fraction of all likely voters who preferred the incumbent at the time of the survey.
and let p be the fraction of survey respondents who preferred the incumbent.
Using the survey results, the estimated value of p is
Answers
Answer:
\(p = \frac{214}{400} = .535 = 53.5\%\)
the full screen guys

Answers
Answer:
(-2 2/3,0)
(0,2)
Step-by-step explanation:
Just did it
Answer:
Step-by-step explanation:
the two points are(0,2), (-8/3,0)

a reliability coefficient determined by the correlation between scores on half of the items on a measure with scores on the other half of the measure is called reliability.
Answers
The reliability coefficient determined by the correlation between scores on half of the items on a measure with scores on the other half of the measure is called split-half reliability.
This method is commonly used to estimate the internal consistency of a measurement instrument. The measure is divided into two halves, and the scores on one half are compared to the scores on the other half using correlation analysis.
A high correlation indicates that the two halves of the measure are consistent and reliable in measuring the same construct. However, split-half reliability assumes that the two halves of the measure are equivalent and that the items are interchangeable, which may not always be the case. Other methods, such as Cronbach's alpha, may be used to assess reliability more accurately.
To know more about reliability:
https://brainly.com/question/21771345
#SPJ4
stuck on this question need some help

Answers
Answer:
1. The graphs of f(x) and h(x) are both quadratic functions with a minimum point. However, the minimum point of f(x) is located at (6,0), while the minimum point of h(x) is located at (2,3).
2. The graphs of g(x) and h(x) both open upwards and are quadratic functions. However, the vertex of g(x) is located at the origin (0,0), while the vertex of h(x) is located at (2,3).
3. The graph of g(x) is a simple parabola that opens upwards, while the graphs of f(x) and h(x) are more complex parabolas with a minimum point and an upward opening. The graph of f(x) is centered at (6,0), while the graph of h(x) is centered at (2,3).
Which operation should you perform first in the expression 12×42?
Answers
Answer:
Muitiplication
Step-by-step explanation:
12x42=504
I would perform the multiplication (12 × 16) last.
A mayor estimates that 4,000 people will attend
the first day of the county fair. A total of 8,400
people actually attend the first day of the fair.
What is the percent error of the mayor's estimate?
Round the answer to the nearest tenth percent, if
necessary.
Answers
Answer:
48%
Step-by-step explanation:
4000÷8400=.476...
.476=48%
Answer:
52.4%
Step-by-step explanation:
A spinner with repeated colors numbered from 1
to 8 is shown. Sections 1 and 8 are purple.
Sections 2 and 3 are yellow. Sections 4, 5, and 6
are blue. Section 7 is orange.
Which statement about probability is true?
The probability of landing on orange is greater
than the probability of landing on purple.
The probability of landing on yellow is less than
the probability of landing on blue.
The probability of landing on orange is equal to
the probability of landing on yellow.
The probability of landing on purple is equal to
the probability of landing on blue.
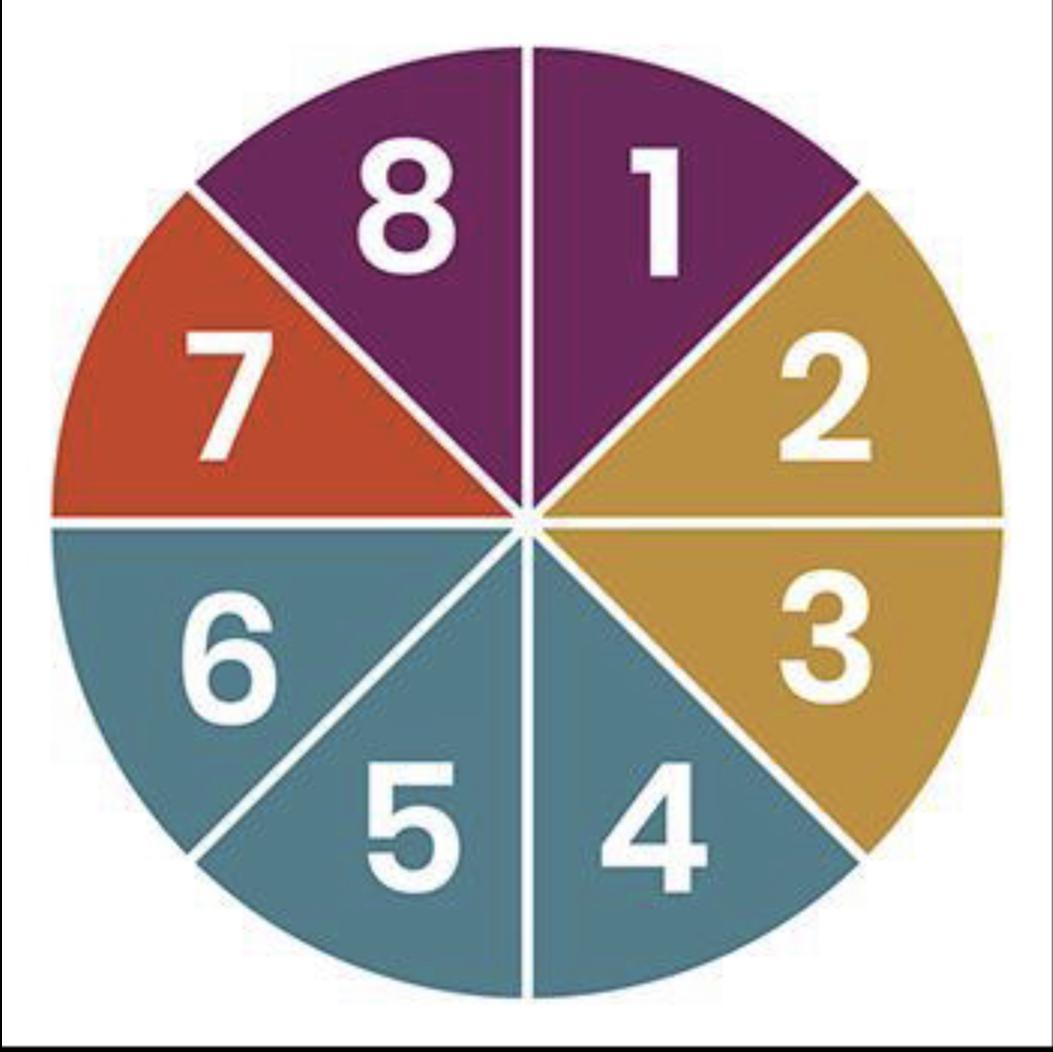
Answers
Answer: The probability of landing on orange is equal to the probability of landing on purple
Step-by-step explanation:
The spinner has a total of 8 equally-sized sections, and each section has a unique color. Therefore, the probability of landing on any particular section is 1/8 or 0.125.
Looking at the colors on the spinner, we can see that there are two purple sections, two yellow sections, three blue sections, and one orange section.
Therefore, the probability of landing on orange is 1/8 or 0.125, which is equal to the probability of landing on purple (sections 1 and 8). So the statement "The probability of landing on orange is equal to the probability of landing on purple" is true.
On the other hand, the probability of landing on yellow is 2/8 or 0.25, which is greater than the probability of landing on blue (sections 4, 5, and 6), which is 3/8 or 0.375. So the statement "The probability of landing on yellow is less than the probability of landing on blue" is false.
Therefore, the correct statement about probability is "The probability of landing on orange is equal to the probability of landing on purple."
One mechanic services 4 drilling machines for a steel plate manufacturer. Machines break down on an average of once every 4 working days, and broakdowns tend to Poisson distribution. The mechanic can handie an average of one repair job per day. Repairs follow a negative exponential distribution: a) On the average, how many machines are waiting for service? The average number of machines waiting for service is (Round your response to three decimal places.)
Answers
Therefore, the average number of machines waiting for service is 0.083 (rounded to three decimal places).
To calculate the average number of machines waiting for service, we can use the concept of the M/M/1 queue, where arrivals follow a Poisson distribution and service times follow a negative exponential distribution.
In this case, the arrival rate (λ) is 1 breakdown every 4 working days, and the service rate (μ) is 1 repair job per day.
The utilization factor (ρ), which represents the system's utilization, can be calculated as ρ = λ/μ = (1/4)/(1) = 1/4.
The average number of machines waiting for service (Lq) can be calculated using the formula Lq = ρ² / (1 - ρ).
Plugging in the values, we have Lq = (1/4)²/ (1 - 1/4) = 1/12.
To know more about average number,
https://brainly.com/question/32640470
#SPJ11
Which function is graphed on the right?

Answers
Answer: \(y=2^{x-2}+3\)
Step-by-step explanation:
To find the equation from a graphed function, you can substitute points into each equation to find the original:
A point on the graph is (2, 4). Substituting this into each equation, we get:
\(4=2^{2+3} -2\), which claims that 4 is equal to 30, which is incorrect.
\(4=2^{2-3} +2\), which claims that 4 is equal to 3/2, which is incorrect.
\(4=2^{2-2}+3\), which claims that 4 is equal to 4, which is correct.
We can test the third function further by taking another point on the graph, (3, 5), and substituting it into the function:
\(5=2^{3-2} +3\), which claims that 5 is equal to 5, which is correct.
Answer:
the answer is C on edge 2020
the answer to the next question is
Sketch the graph of y=7x
Reflect the graph across the y-axis to show the function y=7^-x
Stretch the graph vertically by a factor of 3 to show the function y=3x7^-x
Shift the graph up 2 units to show the function y=3x7^-x +2
Step-by-step explanation:
I NEED HELP ASPA
A small university enrolls in-state and out-of-state students. Enrolled in their most recent freshman class was 243. The school reported that it enrolled seven in-state students for every two out-of-state students. How many of each type of student was enrolled in the freshman class?
Answers
convert 336g to m³
\(336g \: to \: m3\)
Answers
The conversion 336g to m³ is impossible because they measure different units
How to convert 336g to m³From the question, we have the following parameters that can be used in our computation:
Convert 336g to m³
To convert a unit to another, the units must measure the same quantity
Take for instance:
Grams can be converted to kilograms because they both measure mass
Using the above as a guide, we have the following:
336g to m³ cannot be done because of the different quantities they represent
Read more about metric units at
https://brainly.com/question/229459
#SPJ1