Mary has $100. She spends $150. What is her balance?
Answers
Answer:
is this right question ❓
Related Questions
for each of the number lines, write an absolute value equation in the form |x-c|=d, where c and d are some numbers, to satisfy the given solution set.

Answers
An absolute value is the numerical value of a number without consideration of its sign. It can be represented graphically by a straight line known as a number line. Absolute value equations are equations that include absolute values of variables or unknown quantities. The following are examples of how to write an absolute value equation in the form |x-c|=d to fit the provided solution sets:
Example 1:
Solution set: {x|x≤-3 or x≥1}
Absolute value equation: |x-(-1)|=4
Explanation: -1 is the midpoint of the two ranges (-3 and 1) in the solution set. |x-(-1)|=|x+1| is the absolute value expression for the midpoint -1. The distance d from -1 to the solutions' furthest endpoints, 1 and -3, is four, hence the value of d in the absolute value equation is 4.
For such more question on equations
https://brainly.com/question/22688504
#SPJ11
SOLVE FAST I NEED HELP PLEASE FASTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT

Answers
Answer:
36
Step-by-step explanation:
27/3=9
9*4=36
Pls help me with my math

Answers
Answer: -5 < x < 3
Step-by-step explanation:
Subtract 6 from both sides of the equation (-4 and 12, with a result of -10 < x < 6) and then divide by two on both sides (with the result being the answer.
What is the answer? Please

Answers
7. Which of the following illustrates the commutative property of multiplication?
(1) 5(2x) =(5-2)x
(2) 4(2x+5) = 4 - 2x+4-5
(3) x2 +5=5+x2
(4) 2x -3x = 2-3-X-X
show work pleasee
Answers
How is the sum expressed in sigma notation?
22 + 27 + 32 + 37 + 42 + 47
Enter your answer by filling in the boxes.
the sum from i is equal to 1 to blank of open paren close paren$$

Answers
The sum of the arithmetic sequence is S = 207 and the summation notation is S = ∑i=1 to 6 ( 5n + 17 )
What is Arithmetic Progression?An arithmetic progression is a sequence of numbers in which each term is derived from the preceding term by adding or subtracting a fixed number called the common difference "d"
The general form of an Arithmetic Progression is a, a + d, a + 2d, a + 3d and so on. Thus nth term of an AP series is Tn = a + (n - 1) d, where Tₙ = nth term and a = first term. Here d = common difference = Tₙ - Tₙ₋₁
Sum of first n terms of an AP: Sₙ = ( n/2 ) [ 2a + ( n- 1 ) d ]
Given data ,
Let the arithmetic sequence be represented as A
Now , the value of A is
A = 22 + 27 + 32 + 37 + 42 + 47
The number of terms n = 6
So , the value of i ranges from 1 to 6
Now , the summation is represented as ∑i=1 to 6 ( 5n + 17)
when n = 1
S₁ = 5 ( 1 ) + 17 = 22
when n = 2
S₂ = 22 + 5 ( 2 ) + 17
S₂ = 22 + 27
when n = 3
S₃ = 22 + 27 + 5 ( 3 ) + 17
S₃ = 22 + 27 + 32
Hence , the sum of the arithmetic sequence is S = 207
To learn more about arithmetic sequence click :
https://brainly.com/question/1522572
#SPJ1
Please help me solve this angle problem. It is due today!
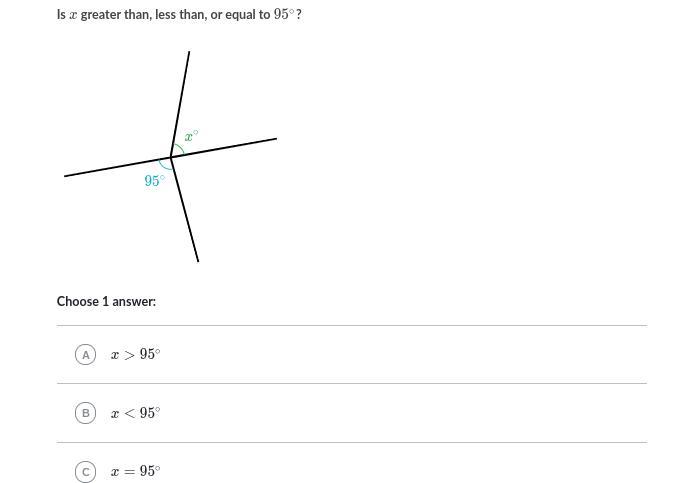
Answers
No explanation
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
!!!Need an answer ASAP!!! A right triangle has a hypotenuse of 16 and a leg of 9. find the length of the other leg.
Answers
Answer:1
Step-by-step explanation:√16 - √9=x
4-3=1
√1=1
Solve. Write or draw to explain. Amy has 12 stickers. Jen has 9 stickers. They place 7 stickers on each page of a book. How many pages are in the book? Math Spot thpicks
Answers
Answer:
There's 3 pages in the book
Step-by-step explanation:
You add both of the amounts of stickers (12+9=21), then you divide by the amount on each page (21÷7=3)
Hope this helped!
round 1456 to nearest 10
Answers
Answer:
1460
Step-by-step explanation:
rounding to the nearest ten, that is nearest to 1456 which would be 1460 (hope this helps! ) ♡
Answer:
1460
Step-by-step explanation:
Original number is 1 4 5 6
To round to the nearest ten, look at the digit in the 10's place and the digit immediately to the right of it
The digit in the tens place is 5
If the digit to the immediate right of this digit is 5 or greater, round the digit in the tens place up by one digit and set the immediate right digit to 0
So 5 rounds up to 6
The 6 to the immediate right(units place becomes 0)
1 4 5 6 rounded to nearest ten==> 1 4 6 0
Find the surface area
of the figure below:
19 cm
30 cm.

Answers
The surface area of the figure is approximately 997.5π cm².
We have,
The figure has two shapes:
Cone and a semicircle
Now,
The surface area of a cone:
= πr (r + l)
where r is the radius of the base and l is the slant height.
Given that
r = 15 cm and l = 19 cm, we can substitute these values into the formula:
= π(15)(15 + 19) = 885π cm² (rounded to the nearest whole number)
The surface area of a semicircle:
= (πr²) / 2
Given that r = 15 cm, we can substitute this value into the formula:
= (π(15)²) / 2
= 112.5π cm² (rounded to one decimal place)
The surface area of the figure:
To find the total surface area of the figure, we add the surface area of the cone and the surface area of the semicircle:
Now,
Total surface area
= 885π + 112.5π
= 997.5π cm² (rounded to one decimal place)
Therefore,
The surface area of the figure is approximately 997.5π cm².
Learn more about cones here:
https://brainly.com/question/13798146
#SPJ1
If the surface area of an orange is 616 cm2 what is its radius?
Answers
9514 1404 393
Answer:
7.0 cm
Step-by-step explanation:
The relationship between radius and area of a sphere is ...
A = 4πr²
Then the radius as a function of area is ...
r = √(A/(4π)) = (√(A/π))/2
For an area of 616 cm², the corresponding radius is ...
r = (√(616/π))/2 ≈ 7.0 cm . . . . radius of the orange
Hope you could understand.
If you have any query, feel free to ask.


Does anyone know the correct answer.

Answers
So 8^2 + 15^2 = hypotenuse^2
Hypotenuse^2 = 289
Hypotenuse = 17 cm
Try this for the second one!!
3
Supplementary Angles measure
(0.5 Points)
degrees. (Knowledge) (S)
180
55
U 90
Answers
supplementary angles measure 180°
Which of these strategies would eliminate a variable in the system of equations?
(2x + 3y = -5
2x - 3y = 10
Choose all answers that apply:
Add the equations.
Subtract the bottom equation from the top equation.
Multiply the top equation by 2. then add the equations.
Answers
Answer:
add the equationssubtract the bottom equation from the top equationStep-by-step explanation:
The coefficients of the x-terms are 2 and 2, so subtracting one equation from the other will give an x-coefficient of 0, eliminating the x-terms. One might choose to subtract the bottom equation, as it is the one with the least y-coefficient. This strategy would result in a y-term with a positive coefficient:
(2x +3y) -(2x -3y) = (-5) -(10)
6y = -15 . . . . . . the result of subtracting the bottom equation
__
The coefficients of the y-terms are 3 and -3, so adding the two equations will give a y-coefficient of 0, eliminating the y-terms.
(2x +3y) +(2x -3y) = (-5) +(10)
4x = 5 . . . . . . the result of adding the two equations.
__
A variable could be eliminated by ...
add the equationssubtract the bottom equation from the top equation_____
Additional comment
The third choice would give ...
2(2x +3y) +(2x -3y) = 2(-5) +(10)
6x +3y = 0 . . . . . . . . eliminates the constant. Both variables remain.
How would you type the answer for GE as in picture for an edpuzzle answer ? What does the check mark symbol mean ?

Answers
Based on the image attached, the solution for GE is approximately 22.72.
What is the expression ?To be able to solve the equation √129 + √129 = GE, one need to simplify the expression and then isolate GE.
Step 1: One can add the square roots:
Note that the equation:
√129 + √129 = GE.
Step 2: Do put together the square root terms:
2√129 = GE.
Step 3: Then Divide by 2:
√129 = GE/2.
Step 4: The Square both sides:
129 = (GE²)/4.
Step 5: So, Multiply by 4:
516 = GE².
Lastly, Take the square root:
√516 = √(GE²)
√516 = GE
GE = 22.72. approx.
Learn more about expression from
https://brainly.com/question/1859113
#SPJ1
See text below
Step 26
Solve the equation for GE:
√129+√129 = GE
GE=2/129
Show steps
foreign direct investment helps improve the economic situation of a recipient country by increasing —- opportunities in the country that the company invests in.
Answers
Foreign direct investment helps improve the economic situation of a recipient country by increasing employment opportunities in the country that the company invests in.
When foreign companies invest in a recipient country, they often establish or expand their operations, which requires hiring local workers. This leads to job creation and reduces unemployment rates in the recipient country.
Increased employment opportunities result in more individuals having access to income and improved standards of living.
Foreign direct investment also contributes to the transfer of technology, knowledge, and skills to the recipient country. Multinational companies often bring advanced technologies, production techniques, and management practices that may not have been available or widely adopted in the recipient country.
Furthermore, foreign direct investment stimulates domestic investment and encourages the growth of local businesses. When foreign companies invest in a recipient country, they often form partnerships or engage in supply chain relationships with local firms.
Overall, foreign direct investment increases employment opportunities, fosters technology transfer, and stimulates domestic investment, all of which contribute to improving the economic situation of a recipient country.
for similar questions on company invests.
https://brainly.com/question/27717275
#SPJ8
Quadrilateral QRST has vertices Q(−1,0), R(2,2), S(5,0), T(−1,−4). Determine whether QRST is a trapezoid and if so, determine whether it is an isosceles trapezoid.


Answers
The quadrilateral QRST is a trapezoid and not an isosceles trapezoid.
What is trapezoid?A trapezoid, also known as a trapezium, is a flat closed shape having 4 straight sides, with one pair of parallel sides.
Given that, a quadrilateral QRST has vertices Q(−1,0), R(2,2), S(5,0), T(−1,−4).
We need tof verify that it is a trapezoid or not, we will find slopes of each side,
Slope = y₂-y₁ / x₂-x₁
Slope QR = 2-0 / 2+1 = 2/3
Slope RS = 0-2 / 5-2 = -2/3
Slope ST = -4-0 / -1-5 = 2/3
Slope QT = -4/0 = not defined
QR ║ ST
Since, two slope are equal therefore, the quadrilateral QRST is a trapezoid
Finding the distance between QS and TR
QS = √(5+1)²+(0-0)² = 6 units
TR = √(-1-2)²+(-4-2)² = √9+36 = √45 = 6.70
Since, QS ≠ TR, it is not an isosceles trapezoid.
Hence, the quadrilateral QRST is a trapezoid and not an isosceles trapezoid.
Learn more about trapezoid click;
https://brainly.com/question/12623349
#SPJ1
PLEASE HELP
IM CONFUSED

Answers
the correct answers are E(-4, 5) and F(3, 2). According to given probabilities condition
How to solve the question?
To find the coordinates of Checkpoints E and F, we need to first understand what is meant by "located at CD's location in a 180° rotation of the course."
A 180° rotation means that we flip the course upside down, with the line segment connecting Checkpoints C and D acting as the axis of rotation. This means that Checkpoints E and F will be on the same line as CD, with E being the reflection of C and F being the reflection of D across the line CD.
To find the coordinates of E, we reflect C across the line CD. To do this, we first find the slope of the line CD:
slope = (2 - 5) / (-3 - (-4)) = -3
The midpoint of CD is:
midpoint = ((-3 + (-4))/2 , (2 + 5)/2) = (-3.5, 3.5)
The line perpendicular to CD passing through the midpoint has slope -1/(-3) = 1/3. Using point-slope form, we can find the equation of this line:
y - 3.5 = (1/3)(x + 3.5)
Simplifying, we get:
y = (1/3)x + 4
To reflect C across CD, we can find the intersection point of this line with the line passing through C and CD. This line has slope -3 and passes through (-4, 5). Using point-slope form, we can find its equation:
y - 5 = (-3)(x + 4)
Simplifying, we get:
y = -3x - 7
Setting these two equations equal to each other, we get:
(1/3)x + 4 = -3x - 7
Solving for x, we get:
x = -4
Substituting this value back into either equation, we get:
y = 5
Therefore, the coordinates of Checkpoint E are (-4, 5).
To find the coordinates of F, we reflect D across CD. We can use a similar method as above to find the line passing through D and CD:
slope = (2 - 5) / (-3 - (-4)) = -3
y - 2 = (-3)(x + 3)
Simplifying, we get:
y = -3x - 7
To reflect D, we find the intersection point of this line with the line perpendicular to CD passing through the midpoint:
y - 3.5 = (1/3)(x - (-3.5))
Simplifying, we get:
y = (1/3)x + 4
Setting these two equations equal to each other, we get:
(1/3)x + 4 = -3x - 7
Solving for x, we get:
x = 3
Substituting this value back into either equation, we get:
y = 2
Therefore, the coordinates of Checkpoint F are (3, 2).
So the correct answers are E(-4, 5) and F(3, 2).
To know more about probability visit :-
https://brainly.com/question/13604758
#SPJ1
A mover places a cylindrical container on a dolly, as shown. Calculate the angle of elevation, U,
from the base of the dolly to the ground.
A. 52.0°
B. 38.0°
C. 38.6°
D. 51.4°
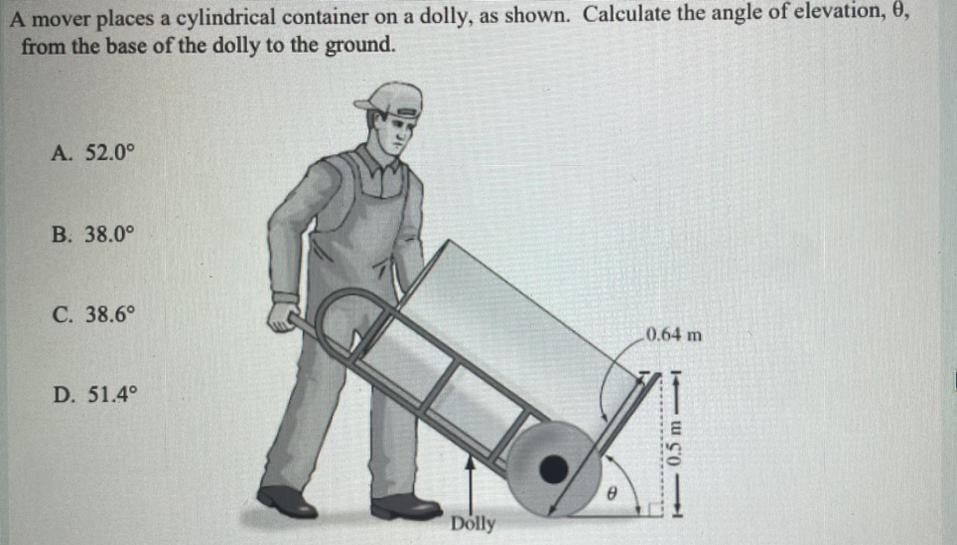
Answers
Check the picture below.
\(\sin( \theta )=\cfrac{\stackrel{opposite}{0.5}}{\underset{hypotenuse}{0.64}} \implies \sin^{-1}(~~\sin( \theta )~~) =\sin^{-1}\left( \cfrac{0.5}{0.64} \right) \\\\\\ \theta =\sin^{-1}\left( \cfrac{0.5}{0.64} \right)\implies \theta \approx 51.4^o\)
Make sure your calculator is in Degree mode.
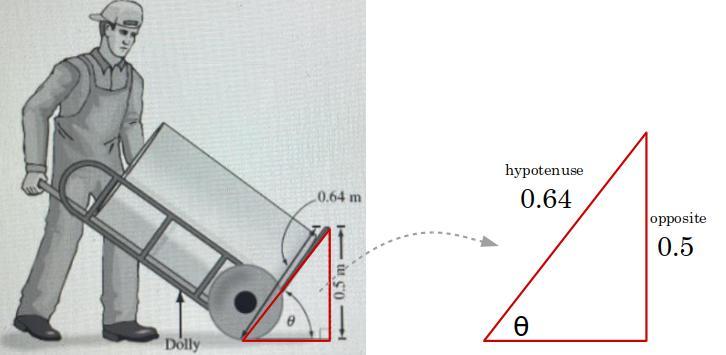
I NEED MAJOR HELP WITH THIS QUESTION
Instriction; using the following image, solve for tbe trigonometry ratios of < D and < F .

Answers
Answer:
Kindly check explanation
Step-by-step explanation:
Since the triangle is right angled ; we can solve for x using Pythagoras :
x = hypotenus ; hence ;
x² = opposite² + adjacent²
x² = 15² + 8²
x² = 225 + 64
x² = 289
x = √289
x = 17
Using Trigonometry :
Sin D = side opposite D / hypotenus = 8/17
Cos D = side Adjacent D / hypotenus = 15 / 17
Tan D = side opposite D / Adjacent side = 8/15
Sin F = side opposite F / hypotenus = 15/17
Cos F = side Adjacent F / hypotenus = 8 / 17
Tan F = side opposite F / Adjacent side = 15/8
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1

PLEASE HELP TODAY I WILL GIVE BRAINLIST

Answers
Answer: Triangle C only
Step-by-step explanation: using the formula to find out if the triangle are right angle (a^2+b^2=c^2) the legs are supposed to equal to the hypotenuse. A and B arentaren't equal to the hypotenuse
Question 9
Which measurement is closest to the distance between point p and point q in units?
14
13
P
12
11
10
9
R
Q
1 2 3 4 5 6 7 8 9 10 11 12 13 14
43
87654321
7
3
0
Answer
A 17 units
B) 13 units
(C) 11 units
D 2.4 units

Answers
Answer:
that means the answer is c
Kelly has 4 times as many songs on her music player as lou. Tiffany has 6 times as many songs on her music as lou. Altogether they 682 songs. How many songs does kelly have?
Answers
kelly has 248 songs on her music player which is 4 times as many songs on as Lou.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Assuming Lou has x no. of songs on her music player.
So, Kelly has 4x songs and Tiffany has 6x songs on their music players.
Altogether they 682 songs.
∴ x + 4x + 6x = 682.
11x = 682.
x = 62 songs.
So, Kelly has 4(62) = 248 songs.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
A data set is given as follows:
Please give the best fit using the least squares with the following functions
(1) y = ax + b;
(2) y = ax + b;
and draw their respective graphs.
(Probability and Statistics)

Answers
Entering the values obtained from the data in the table based on the
given functions of y = a·x + b, and y = a·|x| + b, we have;
(1) y = -0.0614·x + 1.58772
(2) y = 0.3824·x + 0.91168
How can the best fit lines be obtained?The least squares regression formula is presented as follows;
\(a = \mathbf{\dfrac{\sum \left(x_i - \bar x\right) \times \left(y_i - \bar y\right) }{\sum \left(x_i - \bar x\right )^2 }}\)
(1) From the data in the table, and by using MS Excel, we have;
\(\overline x\) = -0.2
\(\overline y\) = 1.6
\(\sum \left(x_i - \bar x\right) \times \left(y_i - \bar y\right)\) = -1.4
\(\sum \left(x_i - \bar x\right )^2\) = 22.8
Which gives;
\(a = \dfrac{-1.4}{22.8 } \approx \mathbf{-0.0614}\)
1.6 ≈ b - 0.0614 × (-0.2)
b = 1.6 - 0.0614 × (0.2) = 1.58772
The equation of best fit for the function, y = a·x + b, is therefore;
y = -0.0614·x + 1.58772(2) For the function, y = a·|x| + b, we have;
\(\overline x\) = 1.8
\(\overline y\) = 1.6
\(\sum \left(x_i - \bar x\right) \times \left(y_i - \bar y\right)\) = 2.6
\(\sum \left(x_i - \bar x\right )^2\) = 6.8
Which gives;
\(a = \dfrac{2.6}{6.8} \approx \mathbf{0.3824}\)
1.6 ≈ b + 0.3824 × (1.8)
b = 1.6 - 0.3824 × (1.8) = 0.91168
The equation of best fit for the function, y = a·|x| + b, is therefore;
y = 0.3824·x + 0.91168Learn more about the least squares regression line here:
https://brainly.com/question/15882801


The Jukes bought a refrigerator for $680. They had to pay 12% down and the remainder in 24 equal installments. How much money did they pay down?
Answers
Answer:
81.6$
Step-by-step explanation:
if 100% =$680
what about 12%
Answer:
81.6$
Step-by-step explanation:
Suppose f is a continuous function on [-2, 2) such that
f(-2) = 1, f(2) = -1
Which of the properties below follow without further restriction on f by applying the Intermediate Value Theorem?
a. f(c) = 0 for some c in (-2, 2).
b. the graph of f(-x) + x crosses the x-axis on (-2, 2);.
c. f(c) < 1 for all c in (-2, 2).
1. b and c only.
2. a and b only.
3. b only.
4. a only
5. c only.
6. a and c only.
7. all of them.
8. none of them.
Answers
Answer:
2. a and b only.
Step-by-step explanation:
We can check all of the given conditions to see which is true and which false.
a. f(c)=0 for some c in (-2,2).
According to the intermediate value theorem this must be true, since the extreme values of the function are f(-2)=1 and f(2)=-1, so according to the theorem, there must be one x-value for which f(x)=0 (middle value between the extreme values) if the function is continuous.
b. the graph of f(-x)+x crosses the x-axis on (-2,2)
Let's test this condition, we will substitute x for the given values on the interval so we get:
f(-(-2))+(-2)
f(2)-2
-1-1=-3 lower limit
f(-2)+2
1+2=3 higher limit
according to these results, the graph must cross the x-axis at some point so the graph can move from f(x)=-3 to f(x)=3, so this must be true.
c. f(c)<1 for all c in (-2,2)
even though this might be true for some x-values of of the interval, there are some other points where this might not be the case. You can find one of those situations when finding f(-2)=1, which is a positive value of f(c), so this must be false.
The final answer is then 2. a and b only.
There are 5 white balls, 8 red balls, 7 yellow balls and 4 green balls in a container. A ball is chosen at random. What is the probability of choosing neither white nor green
Answers
Answer: 5/8
Step-by-step explanation:
i just added all of them & took out the white and green balls ......... oh and i also simplified itAnswer:
The probability is 5/8
Step-by-step explanation:
First, we must add all the numbers together. 5 + 8 + 7 + 4 = 24. Now, let's add the white balls and green balls. 5 + 4 = 9. Therefore, the probability of choosing a white or green ball is 9/24 which also equals 3/8. To find out the probability of NOT choosing white or green, we must subtract 9 from 24. 24 - 9 = 15. So, the probability of choosing neither the white or green balls equals 15/24 which also equals 5/8.
Hope this helps!!