Maria bicycled every day for 14 days. She traveled 294 miles. How many miles did she travel per day?
Answers
Answer:
Maria bicycled 21 miles per day.
Step-by-step explanation:
294/14=21
Hope this helps!
Related Questions
What is the absolute value of | -23|?
Use this number line to determine the absolute value
- 1
22 23
1
1
3
3
Enter your answer in the box as a mixed number in simplest form
Answers
х
y
6
17
10
25
12
29
This relationship is proportional or nonproportional:
The slope is
The y-intercept is

Answers
Slope is 2 or 2x
Y-intercept is 5 or +5
Stress state is given as following.. σ
ij
=
⎣
⎡
20
−4
0
−4
−15
0
0
0
10
⎦
⎤
Calculate normal stress and shear stress acting on a plane perpendicular to direction inclined 30
∘
counter clockwise to σ
11
and direction of three principal stresses and maximum shear stress.
Answers
The normal stress and shear stress acting on a plane perpendicular to direction inclined 30° counter clockwise to σ 11 are σn = 16−15√3 and τ = 2+15√3/4. The maximum shear stress is 17.5.
The stress tensor σ given in the problem is:
σ = 201504−400−1500−1010
The normal stress is given by
σn = σ11cos²θ+σ22sin²θ−2σ12sinθcosθ
where
θ = 30°
θ = 30° is the angle between the direction perpendicular to the plane and the direction of σ11
σ11 = 20
σ22 = −15
σ12 = −4
Here is a detailed calculation:
σn = 20cos²(30)+(-15)sin²(30)-2(-4)sin(30)cos(30)
σn = 20cos²(30)+(-15)sin²(30)+4sin(30)cos(30)
σn = 20(3/4)+(-15)(1/4)+4(1/2)(√3/2)
σn = 12−15√3+4√3
σn = 16−15√3
The normal stress is σn = 16−15√3
The shear stress acting on a plane perpendicular to direction inclined 30° counter clockwise to σ11
σ11 is given by:
τ = σ12(sin²θ−cos²θ)+0.5(σ11−σ22)sin2θ
where
θ = 30°
θ=30° is the angle between the direction perpendicular to the plane and the direction ofσ11.
σ11 = 20
σ22 = −15
σ12 = −4
Here is a detailed calculation:
τ = −4(sin²(30)−cos²(30))+0.5(20−(−15))sin(60)
τ = −4((1/4)−(3/4))+0.5(20+15)(√3/2)
τ = 4(1/2)+0.5(35)(√3/2)
τ = 2+15√3/4
The shear stress is τ = 2+15√3/4
Maximum shear stress
The maximum shear stress is given by
τmax = 0.5(σ1−σ2)
whereσ1σ1 andσ2σ2 are the first and second principal stresses.
The eigenvalues of the stress tensor σ are found by solving the characteristic equation:
det(σ−λI)=0
Here is a detailed calculation:
σ−λI = [20150−λ−400−1500−λ0−400−15−λ10−λ]
σ−λI = 0(20150−λ)[(−λ)(−λ−15)+0(−400)]−(−4)[0(−λ−15)+(−400)(−λ)]+0[0(−400)+(20150−λ)(−λ)]
σ−λI = 0λ³+35λ²−605λ−1875
σ−λI = 0
λ = −25,5,3
The maximum shear stress occurs on the plane of maximum shear stress which is at 45° 45° to the coordinate axes.
The maximum shear stress is found to be
τmax = 0.5(σ1−σ2)
τmax = 0.5(20−(−15))
τmax = 17.5.
Therefore, the maximum shear stress is τmax = 17.5.
Learn more about the normal and shear stress from the given link-
https://brainly.com/question/28485445
#SPJ11
Rewrite each geometry formula using function notation. Use the same variables as the formula in your function. Evaluate each function when r=5 feet. Do not round; write answers in terms of pi, if necessary. Explain the meaning of the result.
a. Diameter, d=2r
The formula using function notation is _______; The value when r=5 is _______; The diameter of the circle is ______ feet when the radius is ________ feet.
b. Area, A=pi x r^2
The formula using function notation is _______; The value when r=5 is _______; The area of the circle is ______ feet when the radius is ________ feet.
c. Circumference C=2 x pi r
The formula using function notation is _______; The value when r=5 is _______; The Circumference of the circle is ______ feet when the radius is ________ feet.
Answers
Answer:
A) d(r) = 2r
Value when r = 5 is 10 ft.
diameter is 10 ft when the radius is 5ft
B) A(r) = πr²
Value when r = 5 is 25π ft²
Area is 25π ft² when radius is 5 feet
C) C(r) = 2πr
Value when r = 5 is 10π
Circumference is 10π when radius is 5 feet
Step-by-step explanation:
A) Using function notation, since d = 2r
d(r) = 2r
d(5) = 2(5)
d(5) = 10 feet
This means that the diameter is 10 ft when the radius is 5ft
B) Area = πr²
In function notation, its;
A(r) = πr²
When radius is 5 feet,
Area is; A(5) = π(5²) = 25π
It means Area is 25π ft² when radius is 5 feet
C) Circumference is 2πr
In function notation, it's;
C(r) = 2πr
When r = 5 feet,
Circumference is;
C(5) = 2π(5)
C(5) = 10π
Please help me answer these 2 questions with a FULL explanation so I know how to do the rest myself. Giving brainliest.

Answers
Answer to 1:
\(\frac{x^3}{2y^25}\)
First thing you want to do is combine like terms on the bottom. Since it's multiplication, all you have to do is add the exponents. So for x you'd get x raised to the -9 power and for y you'd get 2y raised to the power of 7
Second thing is the numerator of the fraction. Since this is raising what is inside the paranthesis to a power, you must multiply this power by the powers of x and y, respectively. You should get x raised to the power of -6 and y raised to the power of -18
Here's where it gets complicated. to rationalize the problem, you must add parts from the numerator and denominator or vice versa. You cannot have any negative exponents anywhere in the fraction. So that means for x you have to add 9 to the x on the top to cancel out the -6 and rationalize the remaining x's. You should end up with x^3.
For y, you work the opposite way. Since the negatives are only on the top, you simply add 18 to the bottom y's and it remains rationalized.
If done correctly this should come out to x^3/2y^25
Answer to 2:
(x^20y^12)/256
First thing you can do on this one is to cancel out the x^0s. Anything to the power of 0 equals one so only the coefficients will remain. Multiply those together and you'll get 4.
Next you will rationalize the ys. Add the bottom 3 to the top to cancel out the denominator and you're left with y^-3. Leave it like this for now.
Now is the difficult part. You must take everything that is inside the parenthesis to the power of -4. That includes the coefficients and the exponents. 4^-4 = 1/256. This means that you now must move the coefficients to the bottom. You should currently have y^-3/(256x^5).
Now take the exponents to the power using the same rules as question 1. -3*-4 = 12 and 5*-4 = -20. You should now have y^12/(256x^-20)
Lastly, we must rationalize the denominator. To do so, move the x^-20 to the numerator and make the exponent positive. After doing this, you have the answer: (x^20y^12)/256
Question 3 Let X1, X2,..., Xn be independent random variables, each having a uniform distri- bution over (0,1). Let M = maximum (X₁, X₂,..., Xn). Show that the distribution function of M, FM(-), is given by FM(x)=x, 0≤x≤1 What is the probability density function of M?
Answers
The distribution function of M, FM(-), is given by FM(x) = x, 0 ≤ x ≤ 1.
The probability density function of M is\(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
In order to understand the distribution function of M, we need to consider the probability that M is less than or equal to a given value x. Since each Xi is uniformly distributed over (0,1), the probability that Xi is less than or equal to x is x.
For M to be less than or equal to x, all of the random variables Xi must be less than or equal to x. Since these variables are independent, their joint probability is the product of their individual probabilities. Therefore, the probability that M is less than or equal to x can be expressed as the product of n x's: P(M ≤ x) = x * x * ... * x = \(x^n\).
The distribution function FM(x) is defined as the probability that M is less than or equal to x. Therefore, FM(x) = P(M ≤ x) = \(x^n\).
To find the probability density function (PDF) of M, we differentiate the distribution function FM(x) with respect to x. Taking the derivative of \(x^n\)with respect to x gives us \(n * x^(^n^-^1^)\). Since the range of M is (0,1), the PDF is defined only within this range.
The distribution function of M is FM(x) = x, 0 ≤ x ≤ 1, and the probability density function of M is \(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
Learn more about probability
brainly.com/question/32575884
#SPJ11
the probability that a specific vulnerability within an organization will be attacked by a threat is known as . a. determinism b. externality c. potential
Answers
The probability that a specific vulnerability within an organization will be attacked by a threat is known as potential.
Potential refers to the likelihood that a specific vulnerability in an organization's security will be exploited by a threat actor or attacker. In the field of information security, the concept of potential is used to assess the risk associated with a particular vulnerability.
This risk assessment helps organizations to prioritize their security efforts and allocate resources where they are most needed. Determinism is a philosophical and scientific concept that refers to the idea that events are determined by prior causes, rather than by random chance.
Externality is an economic term that refers to the impact of an economic activity on parties not directly involved in the activity. For example, pollution from a factory may have externalities that affect the health and well-being of people who live near the factory.
To learn more about vulnerability click on,
https://brainly.com/question/29023407
#SPJ4
An ice cream stand offers single-scoop waffle-cones or bowls. Three flavors are available: strawberry, chocolate, and vanilla. Write the sample space to represent all of the options. How many options are there?
Answers
Answer:
Sample space: 6 Total options: 9
Step-by-step explanation:
The sample space is the amount of variables, this being 6 in total. The options are the total amount of configurations possible with the sample space, this being nine.
I haven't done this in a while so my answer may not be the most reliable, I would use another source if you are still unsure. Good luck!
In ΔEFG, is it possible for segment GE to measure 6 units?
Answers
According to the triangle inequality theorem, the measure for the third side can be GE = 6 units, because: A. 3 + 5 > 6, 5 + 6 > 3, and 6 + 3 > 5.
What is the Triangle Inequality Theorem?The triangle inequality theorem states that the set of side measurements that will form a triangle will be the set of side lengths whereby the sum of any two sides will be greater than the third side of the triangle.
For example, if a, b, and c are the side lengths of a triangle, then:
a + b > ca + c > bb + c > aThus, we have the given lengths:
FE = 3 units
FG = 5 units
Therefore, the third side length would be GE = 6 units based on the triangle inequality theorem because:
3 + 5 > 6
5 + 6 > 3
6 + 3 > 5
Learn more about triangle inequality theorem on:
https://brainly.com/question/309896
#SPJ1

an fbi survery shows that about 30% of all property crimes go solved. suppose that in long island city 5 such crimes are comitted and they are each deemed independent of each toher. what is the prrobabilty that exactly 2 of these 5 crimes will be solved
Answers
The answer is 0.441 using probabilty.
What is Probability ?
Mathematical explanations of the likelihood that an event will occur or that a statement is true are referred to as probabilities.
x:- Number of crimes solved
X = B( n = 5 , p = 0.3 )
P[x ] =\((\frac{n}{x})\)* \(p^{x}\) * \((1-p)^{x}\)
Probabilty that exactly 2 of these 5 crimes will be solved
P[x = 3] = binomial(5,2) * .3² * 0.7³ = 0.441
Hence the probabilty that exactly 2 of these 5 crimes will be solved is 0.441.
Learn more about Probability , by the following link.
brainly.com/question/13604758
#SPJ4
plase answer the second one
thanks

Answers
Answer:
0,01
Step-by-step explanation:
0,0001 = 1 / 10000
√0,0001
= √( 1 / 10000 )
= √1 / √10000
= 1 / 100
= 0,01
what are the answers to fit in the boxes?

Answers
The quantities needed to make multiple loaves of bread can be solved for by multiplying each recipe used for a loaf of bread by number of loaves of bread
Ratio and proportionA loaf of bread
Flour = 2 cupsWater = 12 tablespoonsSalt = 1 teaspoon2 loaves of bread
multiply each ingredients by 2
Flour = 4 cupsWater = 24 tablespoonsSalt = 2 teaspoon3 loaves of bread
multiply each ingredients by 3
Flour = 6 cupsWater = 36 tablespoonsSalt = 3 teaspoon4 loaves of bread
multiply each ingredients by 4
Flour = 8 cupsWater = 48 tablespoonsSalt = 4 teaspoonLearn more about ratio and proportion:
https://brainly.com/question/1781657
#SPJ1
1. Find the percent of area under a normal curve between the mean and−1.18 standard deviations from the mean. (Note that positive indicates above the mean, while negative indicates below the mean.)The percentage of area under a normal curve between the mean and −1.18 standard deviations is2. Find the percent of the total area under the standard normal curve between the following z-scores.z= −1.6 and z = 0.7The percent of the total area between z=−1.6 and z = 0.7 is3. Find the z-score that best satisfies the condition. 36% of the total area is to the left of z.z=
Answers
The percent of area under a normal curve between the mean and −1.18 standard deviations is 38.10% and between z=−1.6 and z = 0.7 is 70.32% and the z-score that best satisfies the condition is z=−0.4.
To find the percent of area under a normal curve between the mean and −1.18 standard deviations from the mean, we need to use a standard normal distribution table or calculator.
The area to the left of −1.18 standard deviations is 0.1190, and the area to the left of the mean is 0.5000. To find the area between them, we subtract the smaller area from the larger area:
0.5000 - 0.1190 = 0.3810
Therefore, the percent of area under a normal curve between the mean and −1.18 standard deviations is 38.10%.
To find the percent of the total area under the standard normal curve between z=−1.6 and z = 0.7, we again need to use a standard normal distribution table or calculator.
The area to the left of −1.6 is 0.0548, and the area to the left of 0.7 is 0.7580. To find the area between them, we subtract the smaller area from the larger area:
0.7580 - 0.0548 = 0.7032
Therefore, the percent of the total area between z=−1.6 and z = 0.7 is 70.32%.
To find the z-score that best satisfies the condition that 36% of the total area is to the left of z, we need to use a standard normal distribution table or calculator.
We look for the z-score that corresponds to a cumulative probability of 0.36. This is approximately −0.4, which means that 36% of the total area under the standard normal curve is to the left of z=−0.4. Therefore, the z-score that best satisfies the condition is z=−0.4.
To Lear learn more about standard deviation and z-score go to:
https://brainly.com/question/17063183#
#SPJ11
using a single composite transformation matrix for k transformations of n points, what is the required number of multiplications?
Answers
The required number of multiplications using a single composite transformation matrix for k transformations of n points is n × k.
In computer graphics, composite transformation matrices are used to transform points and shapes. These matrices are created by combining multiple transformations into a single matrix, allowing for efficient processing of large amounts of data. The number of multiplications required to perform a composite transformation depends on the number of points being transformed and the number of transformations being applied.
If there are n points and k transformations, then the required number of multiplications is n × k.
This is because each point needs to be multiplied by the composite transformation matrix k times.
Therefore, the total number of multiplications is n × k.
To learn more about “transformation matrices” refer to the https://brainly.com/question/20366660
#SPJ11
how many 130lb to kg
Answers
130 pounds weight is equivalent to 59.09 kg.
To convert pounds (lb) to kilograms (kg), you can use the conversion factor of 1 lb = 0.453592 kg. So to convert 130 lb to kg, you would multiply 130 by 0.453592.
This gives you the equivalent weight of 59.09 kg. It's worth noting that the pound is a unit of weight commonly used in the United States and the United Kingdom, while the kilogram is the standard unit of mass in the International System of Units (SI). It's important to use the correct unit of measurement when working with weights and masses in different contexts.
The conversion factor can be memorized or looked up in a conversion table or calculator. It's important to note that the pound and kilogram are both units of measurement for weight, however, the pound is used mainly in the United States and United Kingdom, while the kilogram is widely used across the world and is the standard unit of weight under International System of Units (SI).
To know more about conversion factor on the link below:
brainly.com/question/30166433#
#SPJ11
The diagram shows two right-angled triangles that share a common side. 6 10. Show that x is between 11 and 12.

Answers
We have two right-angled triangles that share a common side, with side lengths 6 and 10. Let's label the sides of the triangles as follows:
Triangle 1:
Side adjacent to the right angle: 6 (let's call it 'a')
Side opposite to the right angle: x (let's call it 'b')
Triangle 2:
Side adjacent to the right angle: x (let's call it 'c')
Side opposite to the right angle: 10 (let's call it 'd')
Using the Pythagorean theorem, we can write the following equations for each triangle:
Triangle 1:\(a^2 + b^2 = 6^2\)
Triangle 2: \(c^2 + d^2 = 10^2\)
Since the triangles share a common side, we know that b = c. Therefore, we can rewrite the equations as:
\(a^2 + b^2 = 6^2\\b^2 + d^2 = 10^2\)
Substituting b = c, we get:
\(a^2 + c^2 = 6^2\\c^2 + d^2 = 10^2\)
Now, let's add these two equations together:
\(a^2 + c^2 + c^2 + d^2 = 6^2 + 10^2\\a^2 + 2c^2 + d^2 = 36 + 100\\a^2 + 2c^2 + d^2 = 136\)
Since a^2 + 2c^2 + d^2 is equal to 136, we can conclude that x (b or c) is between 11 and 12
For more such questions on right angled triangle.
https://brainly.com/question/64787
#SPJ8
If two independent large samples are taken from two populations, the sampling distribution of the difference between the two sample means will have a mean of one. will have a variance of one. can be approximated by a normal distribution. can be approximated by any distribution.
Answers
The statement "the sampling distribution of the difference between the two sample means will have a mean of one" is not necessarily true, and neither is the statement "will have a variance of one" or "can be approximated by any distribution."
The sampling distribution of the difference between two sample means from independent populations will have a mean equal to the difference between the population means. However, the variance of the sampling distribution will depend on the sample sizes and the variances of the two populations.
If the sample sizes are large enough (usually considered to be greater than or equal to 30) and the population variances are known or assumed to be equal, then the sampling distribution of the difference between two sample means can be approximated by a normal distribution.
Therefore, the statement "the sampling distribution of the difference between the two sample means will have a mean of one" is not necessarily true, and neither is the statement "will have a variance of one" or "can be approximated by any distribution." However, the statement "can be approximated by a normal distribution" is generally true if the sample sizes are large enough and the population variances are known or assumed to be equal.
for such more question on sampling distribution
https://brainly.com/question/15713806
#SPJ11
how do you factor 5n^2-13n+6=0 by grouping?
Answers
Answer: 5n²-13n+6=(n-2)(5n-3)=0
Step-by-step explanation:
\(5n^2-13n+6=0\\\\5n^2-10x-3n+6=0\\\\5n(n-2)-3(n-2)=0\\\\(n-2)(5n-3)=0\)
Write the equation for the line through the given point with the given slope. Write equations in slope intercept from.
(4, 0); m = 0
Answers
The Equation of the Line is y = 0 which is the equation is of the X-axis
What is Slope of Line?
The slope is defined as the ratio of "rise" divided by "run" between two points on a line, or the ratio of altitude change to horizontal distance between any two locations on the line.
We are given that the slope of the line is 0
and, the intercept point is (4, 0)
Equation of line: y - y1 = m (x - x1)
y - 0 = 0
y = 0
Implies that the equation is of the X-axis
To learn more about Slope of a Line from the given link
https://brainly.com/question/3493733
#SPJ1
which rotation about its center will carry a regular hexagon onto itself
Answers
1. Ryan bought a brand new car for $18,000. Its value depreciated at a rate of 1. 2%. A. Write a function to represent the value of the car as a function of time. Use technology to estimate the number of years it will take for the value to reach each given amount. B. $17,000 c. $15,000 d. Half of the starting value e. One-third the starting value g. $10,000
Answers
A. To represent the value of the car as a function of time, we can use the formula for exponential decay:
Value = Initial Value * (1 - Rate)^(Time)
In this case, the initial value is $18,000 and the rate of depreciation is 1.2% or 0.012. The function can be written as:
Value = $18,000 * (1 - 0.012)^(Time)
Using technology, such as a calculator or spreadsheet software, you can estimate the number of years it will take for the value to reach each given amount by solving for Time in the above equation. Simply substitute the given value for Value and solve for Time.
B. To find the number of years it will take for the value to reach $17,000, solve the equation:
$17,000 = $18,000 * (1 - 0.012)^(Time)
C. To find the number of years it will take for the value to reach $15,000, solve the equation:
$15,000 = $18,000 * (1 - 0.012)^(Time)
D. To find the number of years it will take for the value to reach half of the starting value ($9,000), solve the equation:
$9,000 = $18,000 * (1 - 0.012)^(Time)
E. To find the number of years it will take for the value to reach one-third of the starting value ($6,000), solve the equation:
$6,000 = $18,000 * (1 - 0.012)^(Time)
G. To find the number of years it will take for the value to reach $10,000, solve the equation:
$10,000 = $18,000 * (1 - 0.012)^(Time)
By solving these equations using technology, you can estimate the number of years it will take for the car's value to reach each given amount based on the given rate of depreciation.
Learn more about exponential here
https://brainly.com/question/30127596
#SPJ11
L+S = 17 3L + 2S=46
Please show your work
Answers
Answer:
S= 5, L= 12
Step-by-step explanation:
To find the value of L and S, we need to first label the 2 equations.
L +S= 17 -----(1)
3L +2S= 46 -----(2)
From (1):
L= 17 -S -----(3) (-S on both sides)
Subst. (3) into (2):
3(17-S) +2S= 46
3(17) -3S +2S= 46 (expand)
51 -S= 46
-S= 46 -51 (-51 on both sides)
-S= -5
S= 5 (divide by -1 throughout)
Subst. S=5 into (3):
L= 17 -5
L= 12
ABCD is inscribed in circle P. find m

Answers
The value of ∠ADC is,
⇒ ∠ADC = 108°.
Since, We know that,
An angle is combination of two rays (half-lines) with a common endpoint. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle.
We have to given that;
In the circle P,
ABCD is inscribed quadrilateral.
And, ∠DAB = 110°,
⇒ ∠ABC = 72°
Hence, To find the value of ∠ADC.
We know that,
Theorem:
A quadrilateral can be inscribed in a circle if and only if the opposite angles are supplementary that is, sum of the opposite angles will be 180°.
Hence, According to the theorem,
⇒ ∠ABC + ∠ADC = 180°
⇒ ∠ADC + 72 = 180
⇒ ∠ADC = 108°
Therefore, We get;
The value of ∠ADC is 108°.
Learn more about the angle visit:;
https://brainly.com/question/25716982
#SPJ1

Suppose a batch of steel rods produced at a steel plant have a mean length of 170 millimeters and a standard deviation of 10. What is the size of a typical sampling error in repeated sampling of = 20 rods? Round to 2 places
Answers
The size of the typical sampling error in repeated sampling of 20 rods would be 5 millimeters.
The concept of sampling error is related to the idea of sampling from a population to estimate a population parameter. It is the difference between the sample statistic (e.g. mean) and the population parameter.
A sampling error in repeated sampling occurs when the mean of a sample differs from the population mean as a result of randomly selecting a sample. In the case of the given problem, the mean of the entire batch of steel rods is 170 millimeters and the standard deviation is 10 millimeters.
The size of the typical sampling error in this case can be estimated using the formula:
Sampling Error = Standard Error × Standard Deviation/Square Root of Sample Size
Plugging in the given values, the sampling error will be:
Sampling Error = 10 × 10/ √20 = 5 millimeters
Therefore, the size of the typical sampling error in repeated sampling of 20 rods would be 5 millimeters.
Learn more about the random sample here:
https://brainly.com/question/12719656.
#SPJ4
Which numbers are a distance of 2 units from 8 on a number line?
(If your answer is wrong I'm deleting it)

Answers
Answer:
10 and 6 I believe
A school math team consists of 3 juniors and 5 seniors. How man different groups can be formed that consist of one junior and 2 seniors
Answers
There are ten ways a committee of five can be formed (all three seniors and two of the five juniors).
Plz Help, and solve. Show your work. I will give Brainliest. A - 7 = -13 solve and show your work 10X - 8 = 9X + 8 Can a right triangle have sides that measure 12, 16, and 20? Show your work and answer.
Answers
Answer:
A - 7 = -13
Add 7
A = -6
10X - 8 = 9X + 8
Add 8
10X = 9X + 16
Subtract 9X
X = 16
In a right triangle, where a and b are the shorter sides, and c is the longer side a^2+b^2=c^2
Thus, plug in the values.
12^2+16^2=20^2
144+256=400
400=400.
Because the equation is true, 12, 16, and 20 can be a right triangle
Hope it helps <3
Answer:
For the first question/equation, A=-6. You can just add seven on both sides.
A-7+7=-13+7 A=-6
For the second question, X=16. You can minus 9x on both sides, then plus 8 on both sides. 10X-9X-8+8=9X-9X+8+8=X=16
For the last one, yes, it can because of 12^2+16^2=20^2. Which simplified is . 144+256= 400. So, yeah. It can be a right triangle.
$8,000 was deposited into an account that was compounded annually at 6% interest over 7 years. How much interest was earned on the account? Interest=(
Answers
Answer:$4029
Step-by-step explanation:
Given
Principal amount \(P=\$8000\)
Interest rate \(R=6\%\)
Time period \(T=7\ yr\)
Amount after T years is given by
\(A=P[1+R\%]^T\)
Put values
\(\Rightarrow A=8000[1+0.06]^7\\\Rightarrow A=\$12,029\)
Interest is the difference of amount and principal, that is
\(\Rightarrow C.I.=12,029-8000=\$4029\)
On a number line, suppose the coordinate of A is 0, and AR = 12. What are the possible coordinates of the midpoint of AR?
The possible coordinates for midpoints of the segment are
?
Answers
The midpoint of AR is (1/2 , 1).
Let the points be:
A(0,0) = (x₁,y₁)
B(1,2) = (x₂,y₂)
Midpoint = (x₁₊x₂/2) , (y₁₊y₂/2)
A location in the middle of a line connecting two points is referred to as the midpoint. The midpoint of a line is located between the two reference points, which are its endpoints. The line that connects these two places is split in half equally at the halfway. In addition, the halfway is reached if a line is drawn to divide the line that connects these two places.
= (0₊1/2) , (0₊2/2)
=(1/2 , 2/2)
= (1/2 , 1)
hence the midpoint of the number line is (1/2 , 1).
Learn more about midpoint form here:
https://brainly.com/question/5566419
#SPJ9
Please help solve :D
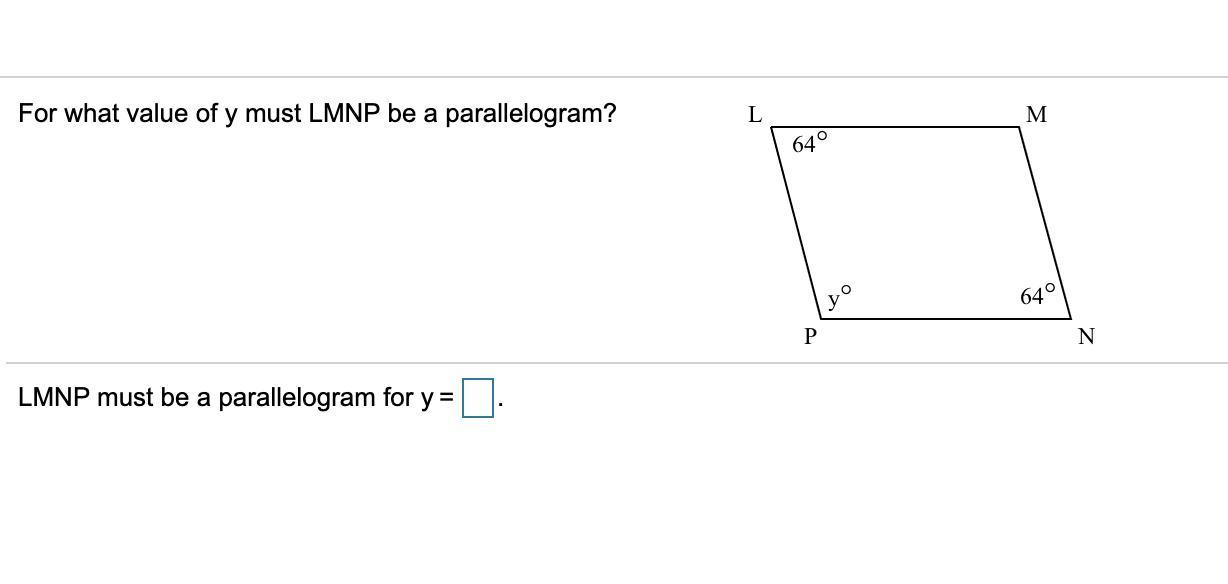
Answers
So y = 180-64 = 116 degrees