Magnus has to play 15 games in a chess tournament. At some point during the tournament Magnus has: ● Won half the games he has played ● Lost one-third of the games he has played ● 2 games have ended in a tie How many games does Magnus have left to play?
Answers
Answer:
3 games left to play
Step-by-step explanation:
Let’s say Magnus has played x games so far. According to the information given, he has won x/2 games and lost x/3 games. The number of tied games is given as 2. So we can write an equation: x/2 + x/3 + 2 = x. Solving for x, we get that Magnus has played 12 games so far. Since he has to play a total of 15 games in the tournament, he still has 15 - 12 = 3 games left to play.
Magnus has played 12 games and he has 3 games left to play in the tournament.
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Let Magnus has played x games, then according to the given information:
He has won half the games he has played, which is equal to (1/2)x.
He has lost one-third of the games he has played, which is equal to (1/3)x.
2 games have ended in a tie.
So, the total number of games played by Magnus is:
x = (1/2)x + (1/3)x + 2
Multiplying by 6
6x = 3x + 2x + 12
Simplifying, we get:
x = 12
Therefore, Magnus has played 12 games so far, and he has 3 games left to play in the tournament.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ2
Related Questions
Is the answer of 18 + pie rational or irrational?

Answers
Answer:
The answer is irrational
Step-by-step explanation:
The number pi is irrational because its digits go on and on in an unpredictable pattern. So if you added 18 to it, it wouldn't change the fact that the numbers in the decimal places are unpredictable.
find the vertex f(x)=2(x+14)^2-6
Answers
Answer:
(-14,-6)
Step-by-step explanation:
what the metric system of measurement is based on the number?
Answers
The metric system of measurement is based on the number 10.
This system is also known as the International System of Units (SI) and is used in most countries around the world. In the metric system, various units of measurement are defined as multiples or fractions of a base unit, which is defined for each quantity being measured. For example, the base unit for length is the meter, and the base unit for mass is the kilogram. Prefixes such as kilo-, centi-, and milli- are used to indicate multiples or fractions of the base unit, based on factors of 10. For example, a kilometer is 1000 meters, a centimeter is 1/100 of a meter, and a milligram is 1/1000 of a gram. This makes the metric system easy to use and convert between units, as well as consistent and universally recognized.
To learn more about the metric system, refer:-
https://brainly.com/question/29953513
#SPJ4
a³+ 1 + 2a² + 2a, a3 - 1 and a²+a2 +1
Answers
HOPE IT HELPS YOU
MARK AS BRAINLIEST

A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472.
Find the substance’s half-life, in days. Round your answer to the nearest tenth.
Answers
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472. The substance's half-life, in days, is approximately 4.7 days.
The half-life of a substance is the time it takes for half of the substance to decay or undergo a transformation. The half-life can be determined using the formula:
t = (0.693 / k)
where t is the half-life and k is the decay constant.
In this case, we are given that the sample has a k-value of 0.1472. We can use this value to calculate the half-life.
t = (0.693 / 0.1472) ≈ 4.7 days
Therefore, the substance's half-life, rounded to the nearest tenth, is approximately 4.7 days.
For more such questions on k-value, click on:
https://brainly.com/question/1978047
#SPJ8
Help tell me the numbers in order

Answers
help meh for brainlist

Answers
Answer:
A. 312
Step-by-step explanation:
For the rectangle center multiply 6*4=24
Area of a trapezoid: ((a+b)/2)h so with this we can determine that the area of one side is 40, since there are 2 sides the area would be 80 total
24+80=104
For 3 bows: 104*3=312
Factorize
4a^2-24a^2b^2+9b^2
Answers

1. 42.78 + 19.56
2. 0.0997 + 1.4
3. $62.74 + $1.75 + $12
4. 40.75 – 17. 46
5. 0.95 – 0.68
6. $60 - $31.74
7. 5.4 x 0.07
8. 5.9 x 1.2
9. 0.24 ÷ 0.8
10. 6.56 ÷ 4
Answers
1. - 62.34
2. - 1.4997
3. - $76.49
4. - 23.29
5. - 0.27
6. - $28.26
7. - 0.378
8. - 7.08
9. - 0.3
10. - 1.64
Answer:
1. 62.34
2. 1.4997
3. $76.49
4. 23.29
5. 0.27
6. $28.26
7. 0.378
8. 7.08
9. 0.3
10. 1.64
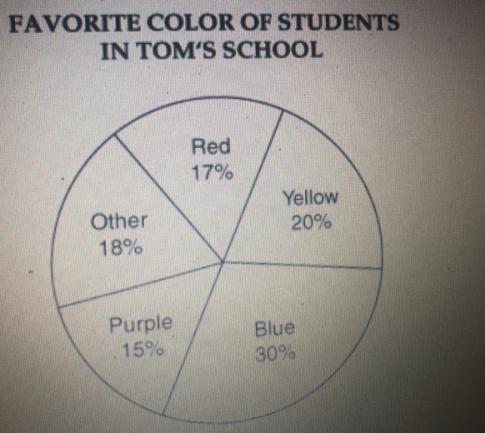
Tom surveyed 150 students at his school to find out each student's favorite color. His results are shown in the circle graph above. Candace asked 15 of her friends from the same school to choose their favorite color, and 5 people chose yellow. According to Tom's survey, how many of Candace's friends would have been expected to choose yellow?

Answers
We have that in Tom's survey he obtained that 20% of the students like the yellow color (see graph above).
Then, in Candance's (small) survey, she asked 15 friends. According to Tom's survey, Candance should have obtained that 20% of her friends like the yellow color.
Therefore, we need to find 20% of 15 (friends) to find the expected number of friends that Candance should have had using the results of Tom's survey. Then, we have:
\(\frac{20}{100}\cdot15=\frac{300}{100}=3\)Hence, according to Tom's survey, Candance's friends would have been expected to be 3 to choose (of her 15 friends) yellow (3 is 20% of 15).
a and b are different numbers selected from the first twenty-five whole numbers: 1 through 25. If a is greater than b, what is the smallest value that the expression below can have?
Answers
The smallest Value that the expression (a - b) can have is 1 when 'a' is 2 and 'b' is 1.
To determine the smallest value that the expression can have, let's analyze the given scenario. We are selecting two different numbers, 'a' and 'b,' from the first twenty-five whole numbers (1 through 25). Since 'a' is stated to be greater than 'b,' we need to find the minimum possible value for the expression.
The expression is not specified, so we'll consider the difference between 'a' and 'b' (a - b) as the expression in this case. To minimize this expression, we need to select the smallest possible values for 'a' and 'b.'
Since 'a' must be greater than 'b' and both 'a' and 'b' are different numbers, the smallest value for 'a' would be 2 (the smallest whole number greater than 1), and the smallest value for 'b' would be 1.
Now we can substitute these values into the expression: (a - b) = (2 - 1) = 1.
Therefore, the smallest value that the expression (a - b) can have is 1 when 'a' is 2 and 'b' is 1.
For more questions on Value .
https://brainly.com/question/843074
#SPJ8
Ten years ago, Rapunzel's hair was 19 cm long. Now her hair is 20,193 cm long.
Approximately how many times as long is Rapunzel's hair now as it was ten years ago?
Answers
Answer:
1065. 1 * 10^3
Step-by-step explanation:
1 *10^3 = 1000Their wanting the ApproximationSolve and graph. Thank you so much!

Answers
Answer:
Step-by-step explanation:
6 + x/2 >= -4
x/2 >= -10
x >= -20
solution is b
What is the TOTAL amount in his account after 2 years
Answers
Answer:
900000000000000
Step-by-step explanation:
what is 2-3 added to 4+6
Answers
Answer:
2-3 is 1 ~
1 + 4 is 5
5+6 = 11
Step-by-step explanation:
So ur answer is 11.
An item sells for $75 and is on sale for 35% off. The sales tax is 9.8%. What is the final cost of the item?
Answers
The final cost of the item after a 35% discount and 9.8% sales tax is $53.54.
The given problem is related to percentage discounts and sales tax and can be solved using the following steps:
Step 1: Firstly, we need to determine the discount amount, which is 35% of the original price. Let's calculate it. Discount = 35% of the original price = 0.35 x $75 = $26.25
Step 2: Now, we will calculate the new price after the discount by subtracting the discount amount from the original price.New Price = Original Price - Discount AmountNew Price = $75 - $26.25 = $48.75
Step 3: Next, we need to calculate the amount of sales tax. Sales Tax = 9.8% of New Price Sales Tax = 0.098 x $48.75 = $4.79
Step 4: Finally, we will calculate the final cost of the item by adding the new price and the sales tax.
Final Cost = New Price + Sales Tax Final Cost = $48.75 + $4.79 = $53.54
Therefore, the final cost of the item after a 35% discount and 9.8% sales tax is $53.54.I hope this helps!
For more such questions on final cost
https://brainly.com/question/29509552
#SPJ8
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
(2.569
3
2. Stephanie has 3 bags of soil to put in her garden. Each bag of soil will cover 125 ft.
How many square feet will Stephanie be able to cover if she uses all these bags of soil?
(7.3A)
Answers
i cant understand your question define briefly
For which value of a does 4 = a +| x – 4| have no solution?
-6
0
4
6
Answers
Answer:
a = 6
Step-by-step explanation:
Hello!
First, let's isolate the Absolute Value bracket.
4 = a + |x - 4|4 - a = |x - 4|Based on the definition of Absolute value, the outcome should always be a positive number. Therefore, if the product, 4 - a, is a negative number, it will have no solutions.
That means a has to be greater than 4 for it to be negative. a should be 6.
a = 6
(01.06 LC)
Expand and simplify: (2x + 5y) (x - 3y) (5 points)
Answers
Answer:
2x² - xy - 15y²
Step-by-step explanation:
(2x + 5y)(x - 3y)
Each term in the second factor is multiplied by each term in the first factor, that is
2x(x - 3y) + 5y(x - 3y) ← distribute parenthesis
= 2x² - 6xy + 5xy - 15y² ← collect like terms
= 2x² - xy - 15y²
Algebra 2 help ASAP... Please I'm being times I have 29mins left!!!!

Answers
Answer: -27a³b⁶ + 8a⁹b¹²
Step-by-step explanation:
a lawyer researched the average number of years served by 45 different justices on the supreme court. the average number of years served was 13.8 years with a standard deviation of 7.3 years. what is the 95% confidence interval estimate for the average number of years served by all supreme court justices? place your limits, rounded to 1 decimal place,
Answers
"a lawyer researched the average number of years served by 45 different justices on the supreme court. the average number of years served was 13.8 years with a standard deviation of 7.3 years.
The 95% confidence interval estimate for the average number of years served by all supreme court justices is [11.2, 16.4].According to the central limit theorem , a sampling distribution of the means is usually distributed in a normal distribution, given a big enough sample size, which means that it has a bell-shaped curve. It has a standard deviation that can be estimated by dividing the population standard deviation by the square root of the sample size. Using the formula below,
we can calculate the 95% confidence interval for the population average.= 13.8 ± (1.96 × 7.3 / √45)
= 13.8 ± (1.96 × 1.088)
= 13.8 ± 2.13The limits are calculated by adding and subtracting the calculated value from the sample mean.13.8 + 2.13
= 15.9313.8 - 2.13
= 11.67Therefore, the 95% confidence interval estimate for the average number of years served by all supreme court justices is [11.2, 16.4].
To know more about average, visit:
https://brainly.com/question/24057012
#SPJ11
Which expression is equivalent to x Superscript negative five-thirds?.
Answers
Answer:
\({\frac{1}{x^{\frac{5}{3} } }\)
Step-by-step explanation:
Apply exponent rule: \(a^{-b}=\frac{1}{a^{b}}\)
So: \(x^{-\frac{5}{3}}={\frac{1}{x^{\frac{5}{3} } }\)
Answer:
1 / 3 sqrt x^5
Step-by-step explanation:
aka B on edge
suppose that 75% of the applicants for a certain industrial job possess advanced training in computer programming. applicants are interviewed sequentially and are selected at random from the pool. find the probability that the first applicant with advanced training in programming is found on the third interview. (round your answer to four decimal places.)
Answers
The probability that the first applicant with advanced training in programming is found on the third interview is 0.0469
Let X denote the number interviewed until 1 has advanced training and follows a geometric distribution with parameter 75%, so
Geometric distribution is: (1-75%)
=0.75
The density function of geometric distribution is,
\(P(X=x)=p(1-p)^{x-1}\), for all x = 1,2,3,....
Now, we calculate the probability that the first applicant with advanced training in programming is found on the third interview:
P(X=3) =\(0.75(1-0.75)^{3-1}\)
=\(0.75(1-0.75)^{2}\)
=0.75×0.0625
=0.0469
Hence, the required probability is 0.0469
Learn more about geometric distribution here:
https://brainly.com/question/25801427
#SPJ4
Find the volume of a cone with radius 12 yd and height 4 yd. Use 3.14 for π. Compare the volumes of the two cones. Use pencil and paper. Pick different values for the radius and height and calculate the volume of two cones like the ones described here. Compare the volumes of these cones.
Answers
Answer:
Volume is 602.88
Step-by-step explanation:
Here, we are asked to
calculate the volume of the cone.
Mathematically, to do this, we need to use the formula for finding the volume of cone= 1/3 * pi *r^2 * h
now we know that radius is 12 yards and height 4 yards. Plugging these values we have;
V = 1/3 * 3.14 * 12^2 * 4
V = 602.88 inches^3
You have two pieces of rope. One piece is of rope is 98 feet and the other is 56 feet. You need to cut the rope into equal lengths with non left over. What is the greatest possible lenth you can cut the rope so all peices will be the same
Answers
Answer:
14 feet
Step-by-step explanation:
We solve the above question by using the Greatest Common Factor method
We find the factors of 56 and 98
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28, 56
The factors of 98 are: 1, 2, 7, 14, 49, 98
Then the greatest common factor is 14.
Therefore, the greatest possible length you can cut the rope so all pieces will be the same is 14 feet
1) Pablo has ten dollars. He wants to buy 7 packs of gum. Each pack of gum costs $1.50. Does hehave enough mones? How do you know?
Answers
Answer:
He does not have enough money, as 10 < 10.50.
Step-by-step explanation:
The first step to solve this question is finding the cost of 7 packs of gum.
1 pack costs $1.50.
So 7 packs will cost 7*1.50 = $10.50.
Pablo has 10 dollars, which is less than $10.50(10 dollars and 50 cents). So he does not have enough money.
Use the Law of Sines to solve the triangle. Round your answers to two decimal places. A = a = C = A O b = 24 C C 104° a 45° B
Answers
Using the Law of Sines, the length of the side c is 33.11 and by using sum of the angles in a triangle is equal to 180° angle B is 31°.
Given, a = b = C = 24, A = 104° and B = 45°.
To find the length of the side c, we use the Law of Sines.
Law of Sines:
sin A/a = sin B/b = sin C/c
Let us find angle A and C.
We know that the sum of the angles in a triangle is equal to 180°.
So, angle B = 180° - (104° + 45°) = 31°
Therefore, angle C = 180° - (104°) - 31° = 45°
Applying Law of Sines, we get sin 104°/24 = sin 45°/c
On solving, we get, c = 33.11°.
Therefore, the length of the side c is 33.11.
We have solved the triangle using the Law of Sines. We have found out the length of the side c which is equal to 33.11.
To know more about Law of Sines visit:
brainly.com/question/13098194
#SPJ11
What are the only two values such that the Fn=n
Answers
Explanation:
Step one:
Substitute the numbers for variables
1(0)=0
Step two:
Solve
1(0) = 0
Step three:
Check your answer
Hopes this helps! <3
Use the First Derivative Test to find the local maximum and minimum values of the function. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) M(t) = 6t^3 +9t^2 - 20t+6. local minimum values = ___. local maximum values = ___.
Answers
The local minimum values are 1, and the local maximum values are 0.
To find the local maximum and minimum values of the function M(t) = 6t³ + 9t² - 20t + 6 using the First Derivative Test, we follow these steps:
Find the derivative of the function:
M'(t) = 18t² + 18t - 20.
Set the derivative equal to zero and solve for t to find the critical points:
18t² + 18t - 20 = 0.
Using the quadratic formula, we get:
t = (-18 ± √(18² - 4(18)(-20))) / (2(18))
t = (-18 ± √(324 + 1440)) / 36
t = (-18 ± √1764) / 36
t = (-18 ± 42) / 36.
Simplifying, we have two possible critical points:
t1 = (-18 + 42) / 36 = 24 / 36 = 2/3
t2 = (-18 - 42) / 36 = -60 / 36 = -5/3.
Analyze the intervals formed by the critical points and the endpoints of the domain:
We consider the intervals (-∞, -5/3), (-5/3, 2/3), and (2/3, +∞).
Test the sign of the derivative in each interval:
For (-∞, -5/3), we choose a test value t = -2. Plugging this value into M'(t), we get M'(-2) = 18(-2)² + 18(-2) - 20 = 72 - 36 - 20 = 16, which is positive.
For (-5/3, 2/3), we choose a test value t = 0. Plugging this value into M'(t), we get M'(0) = 18(0)² + 18(0) - 20 = -20, which is negative.
For (2/3, +∞), we choose a test value t = 1. Plugging this value into M'(t), we get M'(1) = 18(1)² + 18(1) - 20 = 16, which is positive.
Apply the First Derivative Test:
Since the derivative changes from positive to negative at t = 0, this indicates a local maximum. And since the derivative changes from negative to positive at t = 1, this indicates a local minimum.
Therefore, the local minimum value is at t = 1, and the local maximum value is at t = 0.
The local minimum values are 1, and the local maximum values are 0.
To know more about derivative test, visit:
https://brainly.com/question/31402140
#SPJ11