Lucas scored 9 goals in 4 soccer games last season. Approximately how many points did Lucas average per game?
A 0.9
B 7
C 13
D 2.3
Answers
Answer:
D) 2.3
Step-by-step explanation:
9/4 = 2 1/4
Related Questions
Write down the two inequalities that define the shaded region in the diagram

Answers
The two inequalities that define the shaded region in the diagram are:
y ≥ 4 and y < x
How to Write Inequalities that define the Shaded Region?For the solid vertical line, the slope (m) is 0. The inequality sign we would use would be "≥" because the shaded region is to the left and the boundary line is solid.
The y-intercept is at 4, therefore, substitute m = 0 and b = 4 into y ≥ mx + b:
y ≥ 0(x) + 4
y ≥ 4
For the dashed line:
m = change in y / change in x = 1/1 = 1
b = 0
the inequality sign to use is: "<"
Substitute m = 1 and b = 0 into y < mx + b:
y < 1(x) + 0
y < x
Thus, the two inequalities are:
y ≥ 4 and y < x
Learn more about Inequalities on:
https://brainly.com/question/24372553
#SPJ1
Levi bought o oranges at the store. Each orange cost $0.29. Write an algebraic expression to represent how much Levi spent.
Answers
Answer:
0.29x
Step-by-step explanation:
let x be the number of oranges Levi bought
Using the French Academy of Sciences' original definition of the meter, calcula Earth's circumference and radius in those meters. Give \% error relative to today's accepted values (inside front cover).
Answers
The \% error in the Earth's radius calculated using the original definition of the meter is 897.7 \% greater than the accepted value of the Earth's radius. The French Academy of Sciences defined the meter as one ten-millionth of the distance from the equator to the North Pole along a meridian passing through Paris. Therefore, we can calculate the Earth's circumference and radius in those meters as follows:
Circumference of Earth = 40,000 km × 1000 m/km
= 40,000,000 m
Distance between North Pole and equator = 10,000 km × 1000 m/km
= 10,000,000 m1 meter
= 1/10,000,000 of the distance between the North Pole and equator
Therefore, the Earth's circumference = 40,000,000 m / 1 meter/ (1/10,000,000) = 400,000,000 meters
Earth's radius = Earth's circumference / (2 × π) = 400,000,000 / (2 × 3.14) = 63,662,420.38 meters
To find the \% error relative to today's accepted values, we need to compare these values with the values obtained from current measurements.
According to the front cover, the accepted value of the Earth's radius is 6,371 km, which is equivalent to 6,371,000 meters. The \% error in the Earth's radius calculated using the original definition of the meter is:
\% Error = (|Accepted value - Calculated value| / Accepted value) × 100
= (|6,371,000 - 63,662,420.38| / 6,371,000) × 100
= 897.7 \%
Therefore, the \% error in the Earth's radius calculated using the original definition of the meter is 897.7 \% greater than the accepted value of the Earth's radius.
To know more about radius visit :
https://brainly.com/question/13449316
#SPJ11
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
based solely on statistical probability from demographic studies, which individual has the greatest likelihood of being a smoker?
Answers
Based solely on statistical probability from demographic studies, the individual who has the greatest likelihood of being a smoker is a male aged between 18 to 24 years old.
According to demographic studies, men are more likely to smoke than women. Besides, the smoking rate increases with age, which means individuals aged between 18 to 24 have a higher likelihood of being a smoker than people of other ages.
Therefore, based solely on statistical probability from demographic studies, a male aged between 18 to 24 years old has the greatest likelihood of being a smoker.
It is important to note that statistical probability from demographic studies only shows what is likely or probable to happen but does not guarantee the actual occurrence of the event.
To learn more about statistical probability refer :
https://brainly.com/question/30448884
#SPJ11
75 is 1% of_______? Find the Whole
Answers
Answer:
7500
Step-by-step explanation:
Let's call that 'whole' a variable 'x'.
Since 75 is 1% of the whole, we can write this out with numbers and symbols, remembering that 1% of a number is 0.01 times that number
75 = 0.01*x
From there, you can divide both side of the equals sign by 0.01 to find x.
75=0.01x
7500 =x
Answer:
7,500
Step-by-step explanation:
1% of 7,500 is 75
Formula : (Number x 100)/Percent Number = (75x100)/1 = 7,500/1 = 7,500
The hypotenuse of a right triangle measures 15 cm and one of its legs measures 4 cm.
Find the measure of the other leg. If necessary, round to the nearest tenth.
Answers
\(15^2-4^2=225-16\\=209\)
\(\sqrt{209}\)≈14.9
Answer:
14.5
Step-by-step explanation:
15x15=225
4x4=16
225-16=209
The square root of 209 is 14.4568322948.
Which rounds to 14.5
Total pieces of food eaten 57 153 90 food percentage* % % % simulated number of birds in flock for 2nd generation** * divide each flock's total pieces of food by 300, the total number of pieces of food eaten. ** multiply the food percentage for each flock by the total number of birds (30).
Answers
The food percentage would be 19%, 51% and 30%.
Given that we've done it
Number of meals consumed by X = 57
Food consumed by Y = 153.
Number of meals consumed by Z = 90
Total amount of meals consumed = 57 + 153 +90 = 300
Food proportion of flock X thus Equals 57 / 300 * 100 = 19 %
flock food percentage Y =153/300 * 100 = 51 %
flock food percentage Z = 90/300 * 100 = 30 %
This means that the percentages are 19%, 51%, and 30%.
Based on the given information, we have:
Flock X ate 57 pieces of food.
Flock Y ate 153 pieces of food.
Flock Z ate 90 pieces of food.
The total number of pieces of food eaten is 300 (sum of the individual flock's food).
The food percentage for Flock X is 57/300 ≈ 0.19 or 19%.
The food percentage for Flock Y is 153/300 ≈ 0.51 or 51%.
The food percentage for Flock Z is 90/300 = 0.3 or 30%.
The total number of birds for the second generation is 30 (given).
To find the simulated number of birds in each flock for the second generation, we multiply the food percentage for each flock by the total number of birds (30).
For Flock X: 0.19 × 30 = 5.7 (rounded to the nearest whole number: 6 birds)
For Flock Y: 0.51 × 30 = 15.3 (rounded to the nearest whole number: 15 birds)
For Flock Z: 0.3 × 30 = 9 (rounded to the nearest whole number: 9 birds)
Therefore, the simulated number of birds in Flock X, Flock Y, and Flock Z for the second generation are 6, 15, and 9 birds, respectively.
Learn more about whole number here :
brainly.com/question/29766862
#SPJ4
Complete Question
Flock X Flock Y Flock z Total Pieces of Food Eaten 57 153 90 Food Percentage* % 1% % Simulated Number of Birds in Flock for 2nd Generation ** * Divide each flock's total pieces of food by 300, the total number of pieces of food eaten. ** Multiply the food percentage for each flock by the total number of birds (30). DONE
Answer:
19 51 30
6 15 9
second part Is Y then X
Step-by-step explanation:
uhhhh help im extremely lost

Answers
Answer:
B
Step-by-step explanation:
All othe the “big” numbers like 22 become small like 1 as a negative
-17<-3
Vectors u and v are shown on the graph.Part A: Write u and v in component form. Show your work. (3 points)Part B: Find u + v. Show your work. (2 points)Part C: Find 5u − 2v. Show your work. (5 points)

Answers
ANSWER
\(\begin{gathered} (A)u<9,7>;v<8,-2> \\ (B)<17,5> \\ (C)<29,39> \end{gathered}\)EXPLANATION
(A) We want to write the vectors in component form.
To do this, we will write them in terms of their horizontal and vertical lengths.
To do this, we have to find the difference between the coordinate points of the endpoints and the starting points of the vectors.
Hence, for vector u, its starting point is (2, -6) and its endpoint is (11, 1).
Hence, its component form is:
\(\begin{gathered} <11,1>-<2,-6> \\ \Rightarrow<11-2,1-(-6)> \\ \Rightarrow<9,1+6> \\ <9,7> \end{gathered}\)For the vector v, its starting point is (5, 8) and its endpoint is (13, 6).
Hence, its component form is:
\(\begin{gathered} <13,6>-<5,8> \\ \Rightarrow<13-5,6-8> \\ \Rightarrow<8,-2> \end{gathered}\)Hence, the component form of the vectors is:
\(\begin{gathered} u<9,7> \\ v<8,-2> \end{gathered}\)(B) To find the sum of the two vectors, we have to find the sum of their components.
That is:
\(\begin{gathered} u+v=<9,7>+<8,-2> \\ \Rightarrow<9+8,7+(-2)> \\ <17,7-2> \\ <17,5> \end{gathered}\)That is the answer.
(C) To find 5u - 2v, we have to multiply vector u by 5, multiply vector v by 2, and then find the difference:
\(\begin{gathered} 5\lbrack<9,7>\rbrack-2\lbrack<8,-2>\rbrack \\ \Rightarrow<45,35>-<16,-4> \\ \Rightarrow<45-16,35-(-4)> \\ \Rightarrow<29,35+4> \\ \Rightarrow<29,39> \end{gathered}\)That is the answer.
While driving for a rideshare, Mason earns a fixed base amount, as well as a variable per km rate. If he drives
7 km, he earns $17.40. if he drives 12 km, he earns $25.90. Create an equation to model this relation and
then use the equation to determine Mason's earnings if he drives 22.5 km.
PLSS HELP
Answers
Answer:
$43.75
Step-by-step explanation:
Let the 2 situations given represent 2 points on the line. The number of km he drives is the x coordinate, and the amount he earns is the y coordinate:
These 2 points will be (7, 17.4) and (12, 25.9)
Using these points, find the slope using rise over run (y2 - y1) / (x2 - x1)
Plug in the points:
(y2 - y1) / (x2 - x1)
(25.9 - 17.4) / (12 - 7)
8.5 / 5
= 1.7
Next, plug in the slope and a point into y = mx + b to find the y intercept:
y = mx + b
17.4 = 1.7(7) + b
17.4 = 11.9 + b
5.5 = b
Plug the slope and the y intercept into y = mx + b to get the equation:
y = 1.7x + 5.5
Using this, find his earnings if he drives 22.5 km. Plug in 22.5 as x:
y = 1.7x + 5.5
y = 1.7(22.5) + 5.5
y = 43.75
So, if he drives 22.5 km, he will earn $43.75
find the equation of the tangent plane to f(x, y) = x2 − 2xy 3y2 having slope 2 in the positive x direction and slope 2 in the positive y direction.
Answers
The equation of the tangent plane to f(x, y) = x^2 - 2xy + 3y^2, with slopes 2 in the positive x direction and 2 in the positive y direction, is 2x + 4y - 8 = 0.
To locate the equation of the tangent airplane to the floor described with the aid of the feature f(x, y) = \(x^2 - 2xy + 3y^2\), we need to decide the gradient vector and consider it at a given point.
The gradient vector will grant the ordinary vector to the tangent plane, and by way of the use of the slope information, we can discover the equation of the plane.
Calculate the partial derivatives of the feature with recognize to x and y:
f_x = 2x - 2y
f_y = -2x + 6y
Set up a device of equations the use of the given slope information:
f_x = 2
f_y = 2
Solve the machine of equations to discover the factor where the slopes are satisfied:
2x - 2y = 2 --> x - y = 1 --> x = y + 1
-2x + 6y = 2 --> -x + 3y = 1 --> -x = 1 - 3y --> x = 3y - 1
Setting the two expressions for x equal to every other:
y + 1 = 3y - 1
2 = 2y
y = 1
Substitute y = 1 into both expression for x:
x = 1 + 1
x = 2
Therefore, the factor the place the slopes are comfy is (2, 1).
Evaluate the gradient vector at the factor (2, 1):
grad(f) = (f_x, f_y) = (2x - 2y, -2x + 6y)
= (2(2) - 2(1), -2(2) + 6(1))
= (2, 4)
The ordinary vector to the tangent airplane is the gradient vector (2, 4).
Using the point-normal structure of the equation for a plane, the equation of the tangent airplane is:
2(x - 2) + 4(y - 1) + d = 0
To decide the price of d, alternative the coordinates of the factor (2, 1):
2(2 - 2) + 4(1 - 1) + d = 0
0 + 0 + d = 0
d = 0
The equation of the tangent airplane is:
2(x - 2) + 4(y - 1) = 0
Simplifying the equation, we have:
2x - 4 + 4y - 4 = 0
2x + 4y - 8 = 8
For similar question on tangent plane:
https://brainly.com/question/31433124
#SPJ11
what is the volume of the parallelepiped with sides i, 7j − k, and 9i 6j − k?
Answers
The volume of the parallelepiped is 63 cubic units.
The volume of a parallelepiped is the amount of space it takes up. It is calculated by multiplying the lengths of its three sides together.
In this case, the parallelepiped has three sides: i+0j+0k, 0i+7j − k, and 9i+6j − k.
To find the volume, we will use the cross product of two of the vectors. The cross product of two vectors results in a third vector that is perpendicular to both.
The cross product of the first two vectors,
=> (i+0j+0k) x (0i+7j − k) = 7i − 7j − 0k.
The cross product of this vector and the third vector,
=> 9i+6j − k,
results in the vector
=> 63i + 63j − 63k.
The magnitude of this vector is the volume of the parallelepiped.
To calculate the magnitude, we use the Pythagorean theorem and find that it is equal to 63.
To know more about vector here.
https://brainly.com/question/29740341
#SPJ4
a number that multiplies to 30 and adds up to 13
Answers
Answer:
3 and 10
Step-by-step explanation:
a right triangle has side lengths of 12 feet and 5 feet. what is the length, in feet, of the hypotenuse?
Answers
A and B are the side lengths and C is the hypotenuse.
Substitute: 12^2 + 5^2 = c^2
169 = c^2
Square both sides and you're left with:
c=-13 or 13
It has to be the positive one because a length cannot be negative.
Hope this helped!
A shipping container will be used to transport several 120-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 27500 kilograms. Other shipments weighing 12400 kilograms have already been loaded into the container. Which inequality can be used to determine x, the greatest number of
120-kilogram crates that can be loaded onto the shipping container?
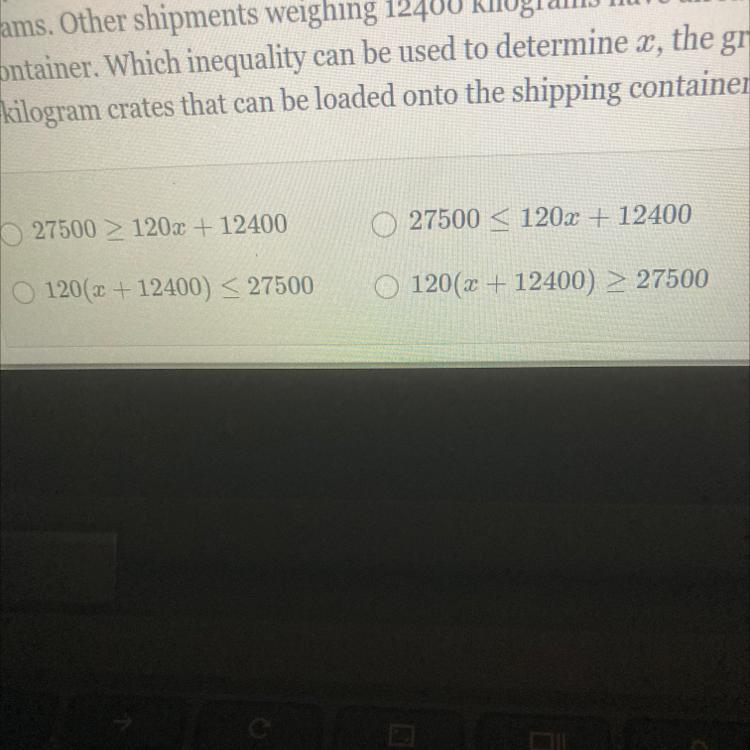
Answers
Inequality can be used to determine x, the greatest number of 120-kilogram crates that can be loaded onto the shipping container is 8000 + 120C <= 27500
What is inequality?An inequality is a relationship that allows us to contrast two or more mathematical expressions.
Knowing that;
Each carton weighs 120 kg.
The container's maximum weight when loaded is 27500 kg.
Weight of the container as it is currently loaded: 8000 kg
Now that we have merged, we have;
Solution
because 8000 grams have already been loaded kilograms
into the container
each crate weighs 120 kilograms.
so 8000 + 120C <= 27500
To learn more about inequality refer to:
https://brainly.com/question/28862943
#SPJ1
yall i need help rn please

Answers
Answer:
D
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
If y = 1/2x, then y will always be half of x.
One-sixth of the 24 students at Aaliyah's school voted for Aaliyah for president. How many students voted for Aaliyah?
Answers
Solve using addition or subtraction 3.9 + t =4.5
Answers
Answer:
0.6
Step-by-step explanation:
subtract 4.5 from 3.9
The distribution of the sample mean, , will be normally distributed if the sample is obtained from a p+opulation that is normally distributed, regardless of the sample size.
Answers
The statement 'The distribution of the sample mean, x overbar, will be normally distributed if the sample is obtained from a population that is normally distributed, regardless of the sample size.' is True
In this question we have been given a statement 'The distribution of the sample mean, x overbar, will be normally distributed if the sample is obtained from a population that is normally distributed, regardless of the sample size.'
We need to state whether the statement is True or False.
We know that the sampling distribution of the sample mean is the probability distribution of all possible values of the random variable x that are computed from a sample of size n.
Also if a random variable X is normally distributed, the distribution of the sample mean, x overbarx, is normally distributed.
Therefore, given statement is True.
Learn more about the sample mean here:
https://brainly.com/question/12421565
#SPJ4
In a Chi-Square test, which of the following is NOT true? If the chi squared test statistic is large, the P-value will be small. Samples are drawn from different populations and we wish to determine whether these populations have the same proportions of the characteristics being considered. Small values of the chi squared test statistic would lead to a decision to reject the null hypothesis. The null hypothesis is that the different populations have the same proportions of specified characteristics.
Answers
The statement that is NOT true in a Chi-Square test is "Small values of the chi squared test statistic would lead to a decision to reject the null hypothesis."
This is because if the test statistic is small, it means that the observed values are close to the expected values, and there is no significant difference between the populations. Therefore, a small test statistic would lead to a failure to reject the null hypothesis. In a Chi-Square test, we compare the proportions of specified characteristics in different populations, and we wish to determine whether they are the same or not. If the test statistic is large, it means that the observed values are significantly different from the expected values, and we have evidence to reject the null hypothesis. Finally, the P-value will be small if the test statistic is large, indicating strong evidence against the null hypothesis.
Learn more about hypothesis here:
https://brainly.com/question/31319397
#SPJ11
who here is doing vlacs?
Answers
Answer:
Not me
Step-by-step explanation:
I am and I REALLY like it
Oh my god wait
I know you...
You are the one who writes like this "What was the economic effect of the Roman conquest. …"
what is the probability that a senior nutrition major and then a sophomore non-nutrition major are chosen at random? express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
Answer: 60%
Step-by-step explanation:
As mentioned earlier, we need to know the number of senior nutrition majors and sophomore non-nutrition majors to calculate the exact probability. Without this information, we cannot provide a specific answer to the question.
However, we can provide a general formula for computing the probability, assuming that the selections are made without replacement and the population of students is large enough to assume independence:
Probability of selecting a senior nutrition major and then a sophomore non-nutrition major = (Number of senior nutrition majors / Total number of students) × (Number of sophomore non-nutrition majors / (Total number of students - 1))
Once we have the values for the number of senior nutrition majors and sophomore non-nutrition majors, we can substitute them into this formula to obtain the probability, which will be a decimal number rounded to four decimal places.
For more details about Probability click here:
https://brainly.com/question/30034780#
#SPJ11
problem 5 (30 points, each 10 points). in a chemical plant, 24 holding tanks are used for final product storage. four tanks are selected at random and without replacement. suppose that four of the tanks contain material in which the viscosity exceeds the customer requirements. 1. what is the probability that exactly one tank in the sample contains high-viscosity material? 2. what is the probability that at least one tank in the sample contains high-viscosity material? 3. in addition to the four tanks with high-viscosity levels, four different tanks contain material with high impurities. what is the probability that exactly one tank in the sample contains high-viscosity material and exactly one tank in the sample contains material with high impurities?
Answers
1. The probability of selecting exactly one tank with high-viscosity material is 0.
2. The probability of selecting at least one tank with high-viscosity material is 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is 0.25.
1. The probability of selecting exactly one tank with high-viscosity material is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 4, x = 1, and p = 24/24 = 1. Therefore, P(X = 1) = (4C1)1^1(1-1)^4-1 = 0.
2. The probability of selecting at least one tank with high-viscosity material is calculated by the complement rule, P(X > 0) = 1 - P(X = 0). In this case, P(X > 0) = 1 - (4C0)1^0(1-1)^4-0 = 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 8, x = 2, and p = 24/24 = 1. Therefore, P(X = 2) = (8C2)1^2(1-1)^8-2 = 0.25.
Learn more about probability here:
https://brainly.com/question/14206287
#SPJ4
Help mee pleaseeeee:((

Answers
Answer:
x≤7
Step-by-step explanation:
Start by solving for x
-12+4x≤16
4x≤28
x≤7
see pic below for the second part

The figures below are similar. The labeled sides are corresponding.
4 cm
P₁ = 12 cm
1 cm
P₂ = ?
What is the perimeter of the smaller rectangle?
P₂=
=
centimeters

Answers
The figures below are similar. By using this, the perimeter of the smaller rectangle P₂ = 3 cm.
What is similar shape?When applying a scale factor, similar shapes are enlarged versions of one another. All of the corresponding angles and lengths in related shapes are equal and in the same ratio.
We divide the length of the enlarged shape by the length of the original shape to calculate the length scale factor.
The ratio of perimeter of both shapes is same as the ratio their corresponding side.
Given that one side of shape 1 is 4 cm and its perimeter P₁ is 12 cm.
and the corresponding side of shape 2 is 1 cm.
comparing the sides and perimeter of both shapes we get
4cm/1cm = 12cm/P₂
by cross multiplication we get,
4 * P₂ = 12cm * 1
P₂ = 12cm/4
P₂ = 3cm
So the perimeter of the smaller rectangle P₂ = 3 cm.
To learn more about similarity of shapes visit:
brainly.com/question/29714189
#SPJ1
1. Luzcel real estate owns 8000 square meters of lot area and decides to construct two different styles of houses, B and C. The lot area of house B is 250 sq. m. and house C lot area is 200 sq. m. The construction engineer has a maximum of 6400 man-hours of labor for the construction. Let your variables be the number of units of house B and the number of units of house C to be constructed. a) Write an inequality which states that there are 8000 sq. m. of land available. b) A unit of house B requires 160 man-hour and a unit of house C requires 256 man-hour. Write an inequality that the engineer has at most 6400 man-hour available for construction. c) If material cost 600 thousand pesos for a unit of house B and 800 thousand for a unit of house C, write an inequality stating that the engineer has at least 12 million pesos to spend for materials. d) Labor cost 1.1 million pesos for constructing a unit of house B and 1.3 million pesos for constructing a unit of house C. If a unit of house B sells for 3.5 million and a unit of house C selis for 4 million, how many units of house B and house C should be constructed to obtain the maximum profit? Show the graph.
Answers
Inequality stating that there are 8000 sq. m. of land available: Let B be the number of units of house B and C be the number of units of house C.
Therefore,B+C ≤ 8000/200 [Reason: House C requires 200 sq. m. of land]⇒B+C ≤ 40b. Inequality that the engineer has at most 6400 man-hour available for construction:
160B + 256C ≤ 6400c
Inequality stating that the engineer has at least 12 million pesos to spend for materials:
600B + 800C ≤ 12000d
. Let us write down a table to calculate the cost, income and profit as follows:Units of house BLabor Hours per unit of house BUnits of house CLabor Hours per unit of house CTotal Labor HoursMaterial Cost per unit of house BMaterial Cost per unit of house CTotal Material CostIncome per unit of house BIncome per unit of house C
Total IncomeTotal ProfitBC=8000/200-B160CB+256C600000800000+256C12,000,0003,500,0004,000,0003,500,000B+C ≤ 40 160B + 256C ≤ 6400 600B + 800C ≤ 12000 Units of house B requires 160 man-hour and a unit of house C requires 256 man-hour.
To know more about number visit:
https://brainly.com/question/3589540
#SPJ11
10. Calculate the following derivatives: dy (a) where dy (b) f(z) where f(x) = az² + b cz²+d (a, b, c, d are constants).
Answers
(a) The derivative of y with respect to x (dy/dx).
(b) The derivative of f(z) with respect to x (f'(x)).
(a) To calculate dy/dx, we need to differentiate y with respect to x. However, without the specific form or equation for y, it is not possible to determine the derivative without additional information.
(b) Similarly, to calculate f'(z), we need to differentiate f(z) with respect to z. However, without the specific values of a, b, c, and d or the specific equation for f(z), it is not possible to determine the derivative without additional information.
In both cases, the specific form or equation of the function is necessary to perform the differentiation and calculate the derivatives.
learn more about derivative's here:
https://brainly.com/question/25324584
#SPJ11
Complete the angle addition postulate for the following angle

Answers
Answer:
measure of angle GEO.....
A tank contains 60 kg of salt and 1000 L of water. Pure water enters a tank at the rate 6 L/min. The solution is mixed and drains from the tank at the rate 3 L/min. (a) What is the amount of salt in the tank initially? (b) Find the amount of salt in the tank after 4.5 hours. (c) Find the concentration of salt in the solution in the tank as time approaches infinity. (Assume your tank is large enough to hold all the solution.)
Answers
Initially, the tank contains 60 kg of salt, calculated by multiplying the salt concentration (0.06 kg/L) by the water volume (1000 L).
In the given scenario, the tank starts with a known salt concentration and water volume. By multiplying the concentration (0.06 kg/L) with the water volume (1000 L), we find that the initial amount of salt in the tank is 60 kg.
After 4.5 hours, considering the rate of water entering and leaving the tank, the net increase in solution volume is 810 L. Multiplying this by the initial concentration (0.06 kg/L), we determine that the amount of salt in the tank after 4.5 hours is 48.6 kg.
As time approaches infinity, with a constant inflow and outflow of solution, the concentration of salt in the tank stabilizes at the initial concentration of 0.06 kg/L.
Learn more about Multiplying click here :brainly.com/question/25834626
#SPJ11