line a has a slope of 5/6 line b is perpendicular to a what is the slope of b?
Answers
Answer:
slope is -6/5
Step-by-step explanation:
A line that is perpendicular to the other the slope will be flipped and minus itself. So if the slope is positive you flip it and make it negative. But if the slope is negative you have to flip it and make it positive because a negative times a negative equals positive.
Related Questions
Calculate the area of the triangular region determined by the points D(-4,3) E(-7,-8) F(-2, -3)
Answers
Answer:
The area is 27
Step-by-step explanation:
Area =1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Area =1/2 [2(-6 - 8) + 3(8 - 4) + 7(4 + 6)]
=1/2 [2(-14) + 3(4) + 7(10)]
=1/2 (-28 + 12 + 70)
=1/2 (54)
Area = 27
Can someone help me with this I don't get it

Answers
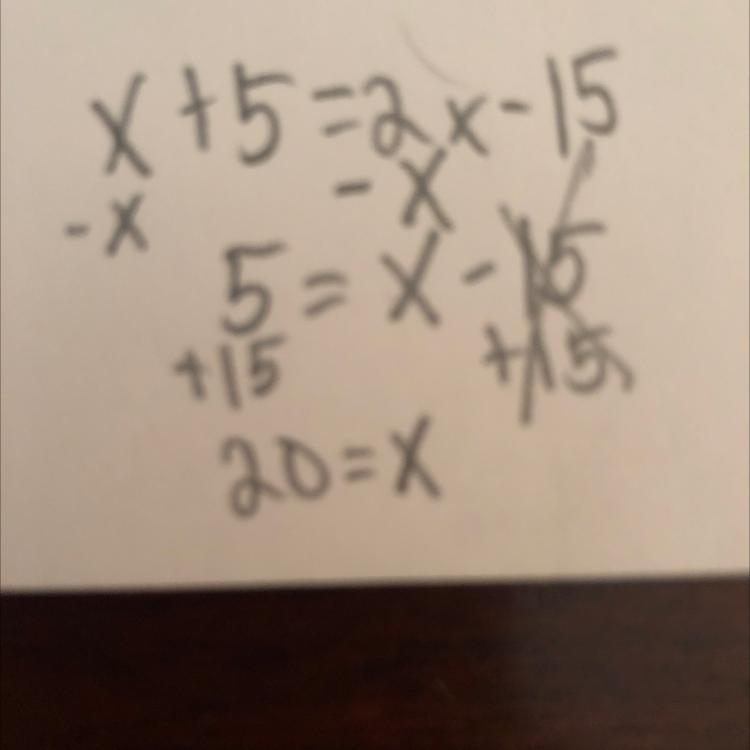
what is the equation of the line that contains the point (2,3) and has a slope of - 3/2
Answers
equation of line
y=mx+b
If m=-3/2
we have
\(\begin{gathered} y=mx+b \\ y=-\frac{3}{2}\cdot x+b \end{gathered}\)From points (2,3), we find b
\(\begin{gathered} y=-\frac{3}{2}\cdot x+b \\ 3=-\frac{3}{2}\cdot2+b \\ 3=-3+b \\ b=6 \end{gathered}\)Therefore
\(y=-\frac{3}{2}\cdot x+6\)8 chairs for every 2 desks, how many chairs for 5 desks?
Answers
Answer:
Step-by-step explanation:
40 desks
do what you gotta do. helppp meh

Answers
Answer:
A
Step-by-step explanation:
11.4-15.7 = -4.3
Answer:
A. -4.3 F
Step-by-step explanation:
Originally you started with 11.4 F, and the question said it decreased by 15.7 F so that basically means you subtract the final condition from initial,
11.4 F - 15.7 = -4.3 F, so at night it was -4.3 F cold.
If you think about this question in terms of apples. Originally I gave you 12 apples to keep for a day. When I returned home at 7pm the numbers of apples decreased by 8. So bascially my final apples will be 12- 8 = 4 apples remaining.
Simplify and Explain Sum:
-7 + 9 - 3 * 6 -(5 + 9) ÷ 7
Answers
Answer:
-18
Step-by-step explanation:
solution....BODMAS
brackets. 5+9
-7+9-3*6-14×7
division 14÷7
multiplication. 3x6
-7+9-18-2
9-27
ans is -18
6z + 3y-(-2y) + 4z. Solve
Answers
Answer: 10z+5y
Step-by-step explanation: 6z + 3y-(-2y) + 4z
6z+3y+2y+4z
6z+4z+3y+2y
10z+3y+2y
10z+5y
If 7 - y = 6, then y =
A. -29
B. -5
C. 1
D. 29
Answers
Answer:
C. 1
Step-by-step explanation:
7 - y = 6
-y + 7 = 6
-y - + 7 - 7 = 6 - 7
-y = -1
(-y=-1)/-1
y = 1
Hope this helps.
\(\sf \bf {\boxed {\mathbb {\: C.\:1}}}\)
\(\large\mathfrak{{\pmb{\underline{\orange{Step-by-step\:explanation}}{\orange{:}}}}}\)
\(7 - y = 6\)
\(➺ \: - y = 6 - 7\)
\(➺ \: - y = - 1\)
\(➺ \: y = 1\)
Therefore the value of \(y\) is 1.
\(\large\mathfrak{{\pmb{\underline{\blue{To\:verify}}{\blue{:}}}}}\)
\(7 - y = 6\)
\(➼ \: 7 - 1 = 6\)
\(➼ \: 6 = 6\)
➼ L. H. S. = R. H. S.
Hence verified.
\(\red{\large\qquad \qquad \underline{ \pmb{{ \mathbb{ \maltese \: \: Mystique35♨}}}}}\)
a sauce recipe calls for 4 pounds of ground beef and you want to halve it how many ounces of ground beef do you need?
Answers
If you want to halve the recipe, you will need 32 ounces of ground beef. We can find it by multiplying.
To determine the amount of ground beef needed when halving the recipe, we need to convert pounds to ounces. There are 16 ounces in 1 pound.
Given that the original recipe calls for 4 pounds of ground beef, we can calculate the amount needed when halving the recipe by dividing it by 2.
Amount needed when halving = 4 pounds / 2 = 2 pounds.
To convert 2 pounds to ounces, we multiply it by 16:
2 pounds * 16 ounces/pound = 32 ounces.
Therefore, when you halve the recipe, you will need 32 ounces of ground beef.
In conclusion, to make half of the original recipe that calls for 4 pounds of ground beef, you will need 32 ounces of ground beef.
For more such questions on multiply, click on:
https://brainly.com/question/29793687
#SPJ8
Write the first three terms of the sequence.
a_n = 2n-1/n^2+5
Answers
Answer:
2a - 1/a^2 +5
The first three terms of the sequence a_n = 2n-1/n²+5 are 1/6, 1/3, and 5/14.
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence.
A sequence is an ordered list of numbers. The three dots mean to continue forward in the pattern established. Each number in the sequence is called a term.
The first three terms of the sequence a_n = 2n-1/n²+5 are:
1. For n=1, a_1 = (2(1)-1)/(1²+5) = 1/6
2. For n=2, a_2 = (2(2)-1)/(2²+5) = 3/9 = 1/3
3. For n=3, a_3 = (2(3)-1)/(3²+5) = 5/14
So, the first three terms of the sequence are 1/6, 1/3, and 5/14.
Learn more about sequence:
https://brainly.com/question/7882626
#SPJ11
legit only or u get banned

Answers
I need helpppp?!!!
What is the slope of the line??
Please give right answer

Answers
Answer: -1/2
Step-by-step explanation:
Slope=rise/run
Up 1 and to the left 2 which makes it a negative
to find this, take two points from the graph. I used (0,3) and (2,2). Then find the difference between the y coordinates and x coordinates. So in this case, the difference between 3 and 2 is 1. And the difference between 0 and 2 is two. And remember it is rise over run so that makes it 1/2. And lastly, you know it's negative because the graph is decreasing. hope this helpsss
A recent study reported that 60% of the children in a particular community were overwoight or obese. Suppose a random sample of 200 public school children is taken from this community. Assume the sample was taken in such a way that the conditions for using the Central Limit Theorem are met. We are interested in finding the probability that the proportion of overveightfobese children in the sample will be greater than 0.57. Complete parts (a) and (b) below. a. Before doing any calculations, determine whether this probability is greater than 50% or less than 50%. Why? A. The answer should be less than 50%. because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. B. The answer should be greater than 50%, because the resulting z-score will be positive and the sampling distribution is approximately Normal. C. The answer should be greater than 50%, because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. 0. The answer should be less than 50%, because the resulting z-score will be negative and the sampling distribution is approximately Normal.
Answers
The probability that the proportion of overweight or obese children in the sample will be greater than 0.57 is less than 50%.
The first paragraph summarizes the answer, stating that the probability is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
In the second paragraph, we can explain the reasoning behind this conclusion. The Central Limit Theorem states that for a large sample size, the sampling distribution of the sample proportion will be approximately normal, regardless of the shape of the population distribution. In this case, the sample was taken in a way that meets the conditions for using the Central Limit Theorem.
Since the population proportion of overweight or obese children is 0.60, any sample proportion below this value is more likely to occur. Therefore, the probability of obtaining a sample proportion greater than 0.57 would be less than 50%. This is because the resulting z-score, which measures how many standard deviations the sample proportion is away from the population proportion, would be negative.
To summarize, the probability of the proportion of overweight or obese children in the sample being greater than 0.57 is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
To learn more about probability click here, brainly.com/question/31828911
#SPJ11
Please! I really need help.

Answers
The answers are given as follows:
2
a)
A = 8
b = 10
x = 118°
y = 62°
b)
a = 8
b = 15
y = 50
x = 100°
3)
(a)
∠2 = 25°
∠3 = 65°
∠4 = 65°
∠5 = 90°
(b)
since SL = 10,
i) LT 10
ii) TM = 10
iii) SM = 10
4)
a) Since m∠118
∠2 = 18°
∠3 = 72°
∠4 = 72°
If FA = 27, then LO = 13.5
The above are resolved using the properties of Parallelograms; Rhombus, and Rectangle
What is the Justification for the above responses?
Since the above answers are justified by the qualities or properties of :
Parallelograms; Rhombus, and Rectangle, lets look at them one by one.
2
a)
A = 8 - opposite sides of a parallelogram are equal in length
b = 10 -opposite sides of a parallelogram are equal in length
y = 62° - opposite angles of a parallelogram are of equal measure.
x = 118° - Sum of angles of a parallelogram - 360°. x = (360 - (62*2))/2
= 118°
3)
(a) Here we have a Rhombus.
∠2 = 25° - Opposite angles of a rhombus are equal; Diagonals bisect the angles of a rhombus. Thus ∠1≅∠2
∠3 = 65° - Since diagonals bisect each other at right angles, ∠3 = 180 - (25+90) = 65°
∠4 = 65° - Diagonals bisect the angles of a rhombus. Thus, ∠3≅∠3
∠5 = 90° - [properties of a Rhombus]
(b)
since SL = 10,
i) LT 10 - All sides of a Rhombus are equal
ii) TM = 10 - All sides of a Rhombus are equal
iii) SM = 10 - All sides of a Rhombus are equal
4) Here we have a Rectangle.
a) Since m∠18
∠2 = 18° because The diagonals bisect each other; and both the diagonals have the same length. Thus, m∠2≅∠1 (AAS)
∠3 = 72° - Each interior angle is equal to 90 degrees. Thus, m∠ = 90-18 = ∠72°
∠4 = 72° - because The diagonals bisect each other; and both the diagonals have the same length. Thus, m∠4≅∠3(AAS)
If FA = 27, then LO = 13.5 - The diagonals bisect each other.Thus,
LO = FA/2
LO = 27/2
LO = 13.5
Learn more about Rectangles:
https://brainly.com/question/15019502
#SPJ1
a right circular cone has a volume of 24\pi24π24, pi cubic inches. if the height of the cone is 222 inches, what is the radius, in inches, of the base of the cone? choose 1 answer: (choice a) a 2 \sqrt{3}2 3
Answers
The cone's base has a radius of 3 inches.The radius of the cone's base measures 3 inches With a base radius of 3 inches, the cone is defined.
The volume of a right circular cone is given by the formula V = (1/3)πr^2h, where V is the volume, r is the radius of the base, and h is the height. In this case, we have V = 24π and h = 2.
Plugging in the given values into the volume formula, we get:
24π = (1/3)πr^2(2)
Canceling out π and multiplying both sides by 3, we have:
72 = 2r^2
Dividing both sides by 2, we get:
36 = r^2
Taking the square root of both sides, we find:
r = 6
Therefore, the radius of the base of the cone is 6 inches.The radius of the base of the cone, given a volume of 24π cubic inches and a height of 2 inches, is 6 inches.
To know more about radius , Visit:
https://brainly.com/question/30295580
#SPJ11
Find the exact length of the curve. x = + y^4/8 + 1/4y^2, 1 <=y<=2
Answers
The exact length of the curve for
x = + y^4/8 + 1/4y^2,
1 ≤ y ≤ 2 is 5.65 units (rounded to two decimal places).
Let's start by computing the derivative of x with respect to y:
dx/dy = y^3/2 + 1/2y
Now, we can use the formula for the length of a curve between y1 and y2:
L = ∫[y1, y2]√[1 + (dx/dy)^2]dy
Substituting dx/dy from above, we get:
L = ∫[1, 2]√[1 + (y^3/2 + 1/2y)^2]dy
This integral is not easy to solve analytically.
Therefore, we can use numerical methods to approximate the value of the integral.
One common method is Simpson's rule. Using Simpson's rule with
n = 4 (four subintervals), we get:
L ≈ (2-1)/12 * [√(1+dx1^2) + 4√(1+dx2^2) + 2√(1+dx3^2) + 4√(1+dx4^2) + √(1+dx5^2)]
where
dxi = dx/dyi
for
i = 1, 2, 3, 4, 5.
Substituting these values, we get:
L ≈ 5.6548...Rounding to two decimal places, we get:
L ≈ 5.65 units.
To know more about exact length visit:
https://brainly.com/question/10707095
#SPJ11
will the sampling distribution of x overbarx always be approximately normally distributed? explain.
Answers
If these conditions are met, the sampling distribution of x will be approximately normally distributed. This is helpful in statistical analyses, as it allows us to make inferences about the population mean using the properties of the normal distribution.
The sampling distribution of x (the sample mean) will be approximately normally distributed if certain conditions are met. These conditions are based on the Central Limit Theorem (CLT), which states that:
1. The sample size (n) is large enough, typically n > 30. This ensures that the sampling distribution of x becomes more normally distributed as the sample size increases.
2. The population from which the sample is drawn is either normally distributed or the sample size is large enough to compensate for non-normality.
The sampling distribution of x overbarx (the sample mean) will be approximately normally distributed if certain conditions are met. These conditions include:
1. The population distribution must be normal or approximately normal.
2. The sample size should be large (typically n > 30).
3. The samples should be randomly selected from the population.
If these conditions are met, the sampling distribution of x will be approximately normally distributed. This is helpful in statistical analyses, as it allows us to make inferences about the population mean using the properties of the normal distribution.
Learn more about population mean:
brainly.com/question/30727743
#SPJ11
my father is 4 times old as me. after 5 years my father will be 3 times old how old is my father now
Answers
Answer:
Step-by-step explanation:

solve for the letter h

Answers
Answer:
v=ha^2/3
Step-by-step explanation:
PLS SOMEONE HELP ME URGENTLY PLS

Answers
The vector z in the component form is z = < 21 , 24 , -27 >
Given data ,
A vector in component form is typically written as an ordered pair or triplet, where each component represents the magnitude of the vector along a specific coordinate axis.
Now , the vector u = < -1 , 3 , 1 >
v = < 4 , -3 , -1 >
w = < 10 , 5 , -10 >
Now , the value of vector z = < 3w - 2v + u >
z = 3w - 2v + u
z = 3w - 2 * < 4 , -3 , -1 > + < -1 , 3 , 1 >
Using scalar multiplication, we get:
z = < 30 , 15 , -30 > - < 8 , -6 , -2 > + < -1 , 3 , 1 >
Adding vectors, we get:
z = < 30 - 8 - 1 , 15 - (-6) + 3 , -30 + 2 + 1 >
z = < 21 , 24 , -27 >
Hence , the vector z in component form is z = < 21 , 24 , -27 >
To learn more about product of vectors click :
https://brainly.com/question/11044032
#SPJ1
pls help i need to show my work fir these problems

Answers
ok so for the first one I'm im taking a guess I think it's the first one.
the second one plot the point on the line between 14 and 15
I think those should be correct I think
Handling Exponents:
Generally when handling exponents it is necessary to follow the different Law of Exponents
1. Product rule
when multiplying exponents with the same base the exponents are added2. Quotient rule
when dividing exponents with the same base the exponents are subtracted3. Power to Power rule
when raising an exponent to another exponent you must multiply them4. Negative exponent rule
when an exponent is raised to a negative power the base is moved to the denominator and the sign of the exponent changes5. Zero power rule
any number raised to the power of 0 = 1In this context we are finding what is equivalent to 6^8 x 6^(-4)
using the product rule, the base is 6 in both cases so we add the exponents: 8 + (-4) = 4now we find what is equivalent to 6^4\(6^(8-4)=6^4\) - this is equivalent
\((6^8)^-4=6^-^3^2\) - not equivalent
\(6^2\) - not equivalent
\(6^-^2=\frac{1}{6^2}\) - not equivalent
\(6^-^3^2=\frac{1}{6^3^2}\) - not equivalent
\(\frac{6^8}{6^4}= 6^(^8^-^4^)=6^4\) - this is equivalent
The first and last options are equivalent to 6^8 x 6^(-4)
p and q are both prime numbers with p < q.
They are each less than 18
Give an example where p + q is odd but not prime.
Answers
The value of p is 2 and q is either 7 or 13 and their sum is either 9 or 15.
It is given that the value of p and q is a prime number, and p<q.
But it is also given that the value of both should be less than 18 as well as a prime number.
Therefore the value of both should be 2, 3, 5, 7, 11, 13, and 17.
And it is also given that p<q.
Now we have to find the value of p + q which is odd but not a prime number.
To have a sum as an odd number one number should be even and as it is given that p<q, therefore p=2, and q = 3, 5, 7, 11, 13, 17.
So
p + q = 2 + 5 = 7, which is odd but it is prime
Now again, q = 7
p + q = 2 + 7 = 9 , which is odd as well as not prime.
Again take q = 11
p + q = 2 + 11 = 13, which is odd but prime
Now take q = 13
p + q = 2 + 13 = 15, which is odd as well as not prime.
Now take q = 17
p + q = 2 + 17 = 19, which is odd and prime.
Therefore we have p =2 and q = 7 or 13 and sum p + q =9 or 15 which is odd but not prime.
To know more about the prime number refer to the link given below:
https://brainly.com/question/792663
#SPJ1
suppose a consumer advocacy group would like to conduct a survey to find the proportion p of consumers who bought the newest generation of an mp3 player were happy with their purchase. a. how large a sample n should they take to estimate p with 2% margin of error, proportion 0.5 and 90% confidence?
Answers
The size of the sample they should take to estimate p with a 2% margin of error and 90% confidence is n = 1691.
In statistics, the margin of error is just the degree of a significant error in the outcomes of random sample surveys.
The formula of margin error is, E = z√((p-vector)(1 - (p-vector)) ÷ n)
E = 2% = 0.02
Confidence level = 90%
Now, the proportion is not given so adopt nominal (p-vector) = 0.05
The critical value at CL of 90% is 1.645.
Thus, making n the subject,
n = z²(((p-vector) × (1 - (p-vector))) ÷ E²)
n = 1.645²((0.5 × 0.5) ÷ 0.02²)
n = 1691.266
n ≈ 1691
Read more about the margin of error at
https://brainly.com/question/16141482?referrer=searchResults
#SPJ4
What is the y intercept of the table

Answers
Answer:
-1
Step-by-step explanation:
Show all of your work and use proper mathematical form and language for full marks.
- A pole 3.8m high casts a shadow 1.3m long. A nearby tree casts a shadow 4.5m long
A. How tall is the tree, correct to one decimal place? Justify your answer.
Answers
The height of the tree is 13.2 m.
What is proportional ?
The concept of proportionality in mathematics denotes the linear relationship between two quantities or variables. The size of one item increases by twofold, whereas the size of the other quantity decreases by one-tenth of the earlier amount.
We can set up a proportion comparing the height of each object to the length of the shadow.
Then , \(\frac{h}{s}\).
=> \(\frac{3.8}{1.3} = \frac{h}{4.5}\)
=> h = \(\frac{3.8*4.5}{1.3}\)
=> 13.2 m.
Hence the height of the tree is 13.2 m.
To learn more about proportional
https://brainly.com/question/870035
#SPJ1
If m vb = 60 and m bs =30 then m 3 =. 30 45 15

Answers
Answer:
Option (3)
Step-by-step explanation:
PB is a tangent and PV, PU are the secants drawn to the circle.
\(m(\widehat {VB})\) = 60° and \(m(\widehat{BS})\) = 30°
By theorem of tangent and secants,
"When a tangent and secant are drawn from a point outside the circle, then the measure of the angle formed is one half the difference of intercepted arcs."
m∠BPV = \(\frac{1}{2}[m(\widehat{BV}-m(\widehat{BS})]\)
m∠3 = \(\frac{1}{2}[60-30]\)
m∠3 = 15°
Therefore, Option (3) will be the answer.
Order from greatest to least, 19/4, 45/10, 4 3/5.
Answers
Answer:
45/10, 4 3/5, 19/4
Step-by-step explanation:
19/4 = 4.75
45/10 = 4.5
4 3/5 = 23/5 = 4.6
4.75 > 4.6 > 4.5
Best of Luck!
Answer:
19/4, 4 3/5, 45/10
Step-by-step explanation:
first you have to divide the fractions TIBO (top in bottom out)
then once you divide them you should get
4 1/2 or 4 5/10 (45/10)
4 3/5 and
4 3/4 (19/4)
since 3/4 is more than half and 3/5 is more than half (2.5 is half of five) but is less than 3/4 is should be 19/4, 4 3/5, 45/10
PLEASE tell me if this is any shape or form helpful to you :)
if not i'm sorry :(
does anyone know how to do simplifying expressions with Distributive property 8th grade math
Answers
Say you have this for a problem
(n+8) + (n -12)
You would then simplify it like this
2n-4
Ay I need help on dis question please

Answers
Step-by-step explanation:
f(x) = (x + 3)^(1/3)
We notice that f(x) is a strictly increasing function.
Hence,
Minimum value of f(x) is when x = -11,
f(x) = (-11 + 3)^(1/3) = -2.
Maximum value of f(x) is when x = 5,
f(x) = (5 + 3)^(1/3) = 2.
P.S. You can differentiate f(x) to show that it is an increasing function.
PLS HELP THANK YOU I REALLY NEED IT

Answers
Answer:
25
Step-by-step explanation:
x+115=180 (straight angle)
x= 65
y= 180-90-65
=25