Let
A = {1, 3, 5, 7, 9},
B = {3, 6, 9},
and
C = {2, 4, 6, 8}.
Find each of the following. (Enter your answer in set-roster notation. Enter EMPTY or ∅ for the empty set.)
(a). A ∪ B
(b). A ∩ B
(c). A ∪ C
(d). A ∩ C
(e). A − B
(f). B − A
(g). B ∪ C
(h). B ∩ C
Answers
The result of the each of the following set is
A ∪ B = {1, 3, 5, 6, 7, 9}
A ∩ B = {3, 9}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A ∩ C = {∅}
A - B = {1, 5, 7}
B - A = {6}
B U C = {2, 3, 5, 6, 8, 9 }
B ∩ C = {6}
The given values are
A = {1, 3, 5, 7, 9}
B = {3, 6, 9}
C = {2, 4, 6, 8}
Then find the each given terms in set roaster notation
Union of the set, intersection of the set and the difference of the set are the basic operations of set
A ∪ B = {1, 3, 5, 6, 7, 9}
A ∩ B = {3, 9}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A ∩ C = {∅}
A - B = {1, 5, 7}
B - A = {6}
B U C = {2, 3, 5, 6, 8, 9 }
B ∩ C = {6}
Therefore, all the given terms has been found
Learn more about set here
brainly.com/question/29055360
#SPJ4
Related Questions
State if the three side lengths form an acute obtuse or a right triangle
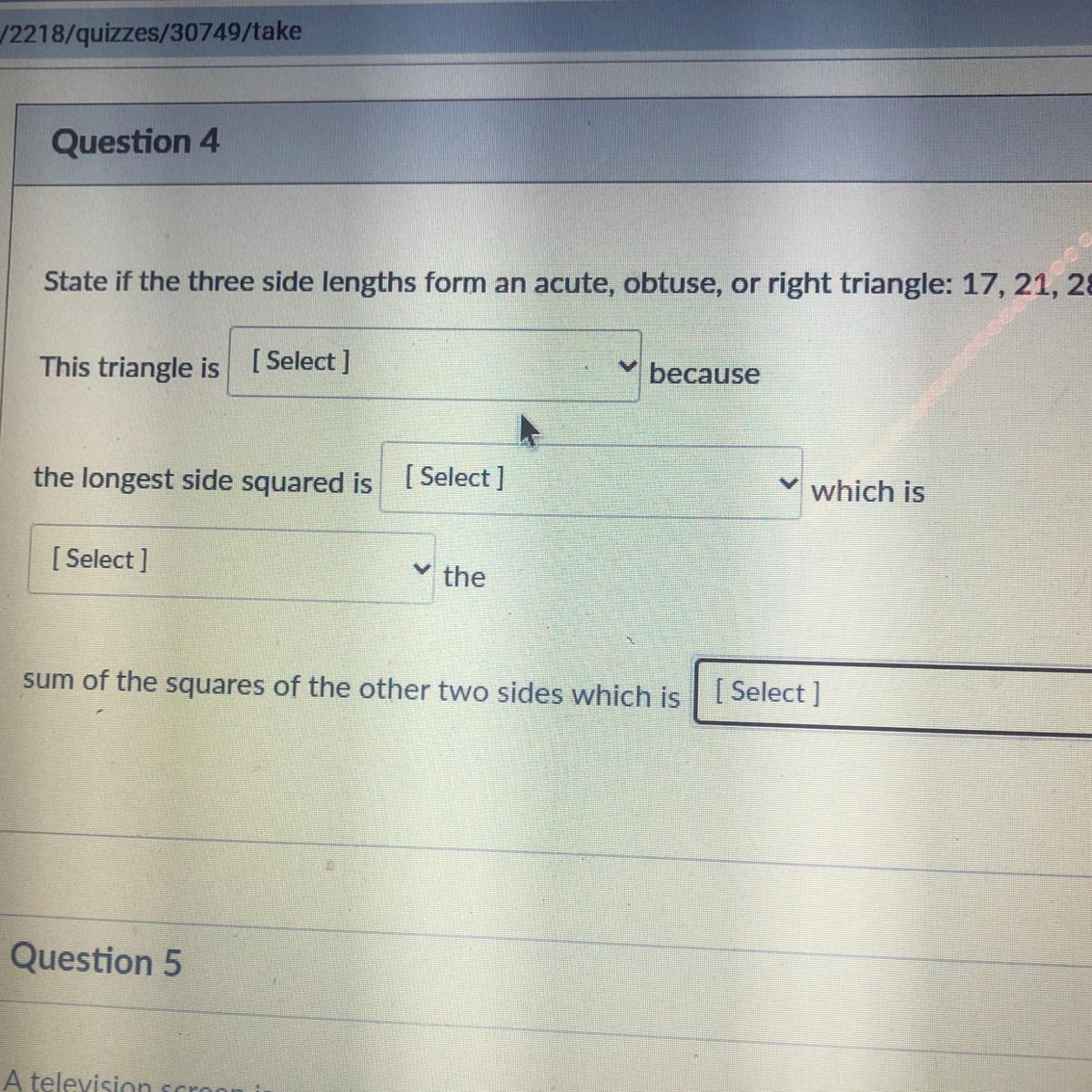
Answers
Given three side lengths form an acute obtuse or a right triangle 17, 21, & 28
Check Right triangle
\(\begin{gathered} Hyp^2=opp^2+adj^2 \\ 28^2=17^2+21^2 \\ 28^2\text{ = 289 +441} \\ 784\text{ }\ne\text{ 730} \end{gathered}\)Not a Right triangle
An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry.
Not an Obtuse triangle
\(\begin{gathered} \sin \text{ A= }\frac{opp}{hyp} \\ \sin \text{ A = }\frac{17}{28} \\ A=sin^{-1}\text{ }\frac{17}{28} \\ A=37.4^0\text{ (less than 90)} \end{gathered}\)\(\begin{gathered} \cos \text{ B = }\frac{adj}{hyp} \\ \cos \text{ B = }\frac{21}{28} \\ B=cos^{-1}\frac{21}{28} \\ B=41.4^0\text{ (less than 90)} \end{gathered}\)\(\begin{gathered} \tan \text{ C = }\frac{opp}{adj} \\ \tan \text{ C = }\frac{17}{21} \\ C=tan^{-1\text{ }}\frac{17}{21}\text{ } \\ C=38.9^0\text{ (less than 90) } \end{gathered}\)Hence it is acute angle because all angles are less than 90°

I need help please I’m very confused

Answers
The values of d that make the inequality 9d > 9 true are given as follows:
2, 4, 11.
Hence the equivalent inequality is given as follows:
d > 1.
How to solve the inequality?The inequality in the context of this problem is defined as follows:
9d > 9.
To solve the inequality, we solve it similarly to an equality, isolating the desired variable d, hence the solution is given as follows:
d > 9/9
d > 1.
The > symbol means that the solution is composed by values that are greater than 1, hence the options are 2, 4, 6 and 11.
More can be learned about inequalities at brainly.com/question/25275758
#SPJ1
Suppose a triangle has two sides of length 2 and 5 and that the angle
between these two sides is 60°. What is the length of the third side of the
triangle?
O A. J9
OB. 3
OC. 23
OD. 5
Answers
Answer:
please what did you put as the first option
Step-by-step explanation:
I think the answer is 29
formation about a sample is given. Assume that the sampling distribution is symmetric and bell-shaped. P_1 - P_2 = 0.15 and the margin of error for 95% confidence is 5%. (a) Indicate the parameter being estimated.(b) Use the information to give a 95% confidence interval.
Answers
(a) Parameter being estimated in the given information is the difference between two proportions (p_1 - p_2).
(b) A 95% confidence interval is given by (0.075, 0.225)
(a) The parameter being estimated is the difference between two population proportions, which is denoted by (p_1 - p_2).
(b) The margin of error for a 95% confidence interval is 5%, which means that the critical value of z is 1.96 (obtained from a standard normal distribution table). Using the formula for the margin of error, we can write:
1.96 * √(p_1_hat*(1-p_1_hat)/n_1 + p_2_hat*(1-p_2_hat)/n_2) = 0.05
where p_1_hat and p_2_hat are the sample proportions from the two samples, and n1 and n2 are the sample sizes.
Solving for p_1_hat - p_2_hat, we get:
p1_hat - p2_hat = ±0.075
Since we are interested in a 95% confidence interval, we can subtract and add this value from P1 - P2 to obtain the interval:
P_1 - P_2 ± 0.075
Substituting the given value of P_1 - P_2 = 0.15, we get:
95% Confidence Interval: (0.075, 0.225)
To know more about the "confidence interval" concept: https://brainly.com/question/17097944
#SPJ11
PLS help me i need the answer asap 7th grade math

Answers
Answer:
The answer is C ≈ 86.7 cm
Answer:
The answer is 86. 7
Step-by-step explanation:
\(c = 2\pi \times r \\ c = 2 \times 3.14 \times 13.8 \\ c = 86.742857 \ \\ \)
Then C to the nearest tenth is
\(c = 86.7\)
a school has 8 students and 3 teachers. they need to form a line to enter the auditorium. if the line starts with a teacher and ends with a student, how many ways can they line up?
Answers
The total number of ways students and teachers line up according to given condition is equal to 840.
Total number of students in a school = 8
Total number of teachers in a school = 3
Since the line must start with a teacher and end with a student,
Consider them as fixed positions in the line.
Arrange the remaining 7 people in the middle of the line.
First, choose one of the three teachers to be at the front of the line in 3 ways.
Then, choose one of the 8 students to be at the end of the line in 8 ways.
Next, arrange the remaining 4 teachers and 3 students in the middle of the line.
This can be done in 7!/(4!3!) = 35 ways,
Using the formula for combinations with repetition.
The total number of ways to form the line is equal to
= 3 x 35 x 8
= 840
Therefore, there are 840 ways they can line up.
Learn more about ways here
brainly.com/question/29186830
#SPJ1
1 0 0 -3
a. 0 1 0 0
0 0 1 7
1 -3 0 0
b. 0 0 1 0
0 0 0 1
Suppose that the augmented matrix for a linear system has been reduced by row operations to the given row echelon form. Identify the pivot rows and columns and solve the system.
Answers
The solution is (3, 1). Hence, the system has a unique solution.
The augmented matrix of the linear system is given below:100-30001The augmented matrix is already in row echelon form. Row echelon form is a form in which the elements below the leading coefficients are all zero. In this matrix, the first non-zero element of the first row is 1, which is called a leading coefficient.
Therefore, the first row is a pivot row. The pivot column is the column in which the pivot row's leading coefficient appears.In this case, the first column is the pivot column. The second row has only one non-zero element, which is also a leading coefficient. Thus, the second row is also a pivot row.
The pivot column for the second row is the third column. Since there are two pivot rows, there will be two variables in the system. Assign x1 and x2 to the first and second columns, respectively. The linear system is: x1 - 3x2 = 0, x3 = 1x1 = 3x2 x2 = x2 x3 = 1.
The solution to this system is (3t, t, 1), where t is a free variable. The solution is a line since there is one free variable, t. The solution can be represented parametrically as a line in three dimensions. The solution can be represented as a point in two dimensions since there are two variables in the system. The solution is (3, 1). Hence, the system has a unique solution.
To know more about echelon form refer here :
https://brainly.com/question/30978124
#SPJ11
If f(x) = 2x^2 - 5 and g(x) = 3x3, find (f-g)(x).
Answers
\(\text{Given that,}~ f(x) = 2x^2 -5 ~ \text{and}~ g(x) = 3x^3\\\\\text{Now,}\\\\ ~~(f-g)(x)\\\\=f(x) - g(x)\\\\=2x^2 -5 - 3x^3\\\\=-3x^3 +2x^2 -5\)
The time (in hours) required to repair a machine is an exponentially distributed random variable with parameter lambda = 1/2 . What is:
(a) the probability that a repair time exceeds 1/2 hours?
(b) the conditional probability that a repair takes at least 10 hours, given that its duration exceeds 9 hours?
Answers
The conditional probability that a repair takes at least 10 hours, given that its duration exceeds 9 hours, is approximately 0.0067 / 0.0037 ≈ 1.81.
(a) To find the probability that a repair time exceeds 1/2 hours, we need to calculate the complementary probability of the repair time being less than or equal to 1/2 hours. The exponential distribution has a cumulative distribution function (CDF) given by F(x) = 1 - e^(-λx), where λ is the parameter. Using this formula, we can calculate the probability: P(X > 1/2) = 1 - P(X ≤ 1/2) = 1 - (1 - e^(-λ(1/2))) = 1 - (1 - e^(-1/4)) = e^(-1/4) ≈ 0.7788. Therefore, the probability that a repair time exceeds 1/2 hours is approximately 0.7788. (b) To find the conditional probability that a repair takes at least 10 hours, given that its duration exceeds 9 hours, we need to calculate the ratio of the probability of the repair taking at least 10 hours and the probability of the repair time exceeding 9 hours. P(X ≥ 10 | X > 9) = P(X ≥ 10 and X > 9) / P(X > 9). The probability that the repair time exceeds 9 hours is the same as the probability that the repair time exceeds 9 hours or 10 hours. P(X > 9) = 1 - P(X ≤ 9) = 1 - (1 - e^(-λ(9))) = 1 - (1 - e^(-9/2)) = e^(-9/2) ≈ 0.0037.
The probability that the repair time exceeds both 9 and 10 hours is the same as the probability that the repair time exceeds 10 hours. P(X ≥ 10 and X > 9) = P(X ≥ 10) = 1 - P(X ≤ 10) = 1 - (1 - e^(-λ(10))) = 1 - (1 - e^(-5)) = e^(-5) ≈ 0.0067. Therefore, the conditional probability that a repair takes at least 10 hours, given that its duration exceeds 9 hours, is approximately 0.0067 / 0.0037 ≈ 1.81.
To learn more about conditional probability click here: brainly.com/question/10567654
#SPJ11
Ayden ran 2 7/8 laps. eduardo ran 1 1/4 laps. how much farther did ayden run than eduardo?
1 5/8
3 8/12
1 6/4
4 1/8
Answers
Answer:
1 5/8
Step-by-step explanation:
2 7/8 - 1 1/4 = 1 5/8.
hope this helps :)
Just need the answer thank you

Answers
Answer:
The multiplicative rate of change is 3/4
Step-by-step explanation:
Here, we want to get the multiplicative rate of change
In this case, by dividing the succeeding term by the preceding term, we will get the multiplicative rate of change
mathematically, we have this as;
81/128 divided 27/32
= 81/128 * 32/27
= 3/4
The angle by which AB turns clockwise about point B to coincide with BC is _ degrees. If from point B, a point E is drawn directly opposite point C so that B, E, and C are on the same straight line, the angle by which AB turns counterclockwise to coincide with BE is _ degrees.
Answers
The requried, to find the angle by which AB turns clockwise about point B to coincide with BC, we need to first identify points A, B, and C on a diagram.
What is the transformation of geometry over the coordinate plane?Transform the shapes on a coordinate plane by rotating, reflecting, or translating them. Felix Klein introduced transformational geometry, a fresh viewpoint on geometry, in the 19th century.
Here,
To find the angle by which AB turns clockwise about point B to coincide with BC, we need to first identify points A, B, and C on a diagram. Once we have done that, we can draw a line from B to C, and then compare the direction of AB to the direction of BC. The angle between these two lines will be the angle by which AB turns clockwise to coincide with BC.
Similarly, to find the angle by which AB turns counterclockwise to coincide with BE, we need to identify points A, B, C, and E on a diagram. Once we have done that, we can draw a line from B to E, and then compare the direction of AB to the direction of BE. The angle between these two lines will be the angle by which AB turns counterclockwise to coincide with BE.
Learn more about transformation here:
brainly.com/question/18065245
#SPJ1
Solve 4a^4 - 8a^2+4 = 0 for a and list all of the solutions. Explain how you got your answer.
Answers
\(4a^4-8a^2+4=0\implies 4(a^4-2a^2+1)=0\implies a^4-2a^2+1=0 \\\\\\ (a^2)^2-2a^2+1=0\implies (a^2-1)(a^2-1)=0\implies a^2=1 \\\\\\ a=\pm\sqrt{1}\implies a=\pm 1\)
Sarkis wants to draw a triangle with sides measuring 4 ft, 10 ft, and 16 ft. Which is true about Sarkis’s plan?
the options are
Sarkis cannot draw a triangle with these side lengths.
Sarkis can only draw one unique triangle with these side lengths.
Sarkis can draw exactly two triangles with these side lengths.
Sarkis can draw more than one triangle with these side lengths.
Answers
Answer:
she cant
Step-by-step explanation:
Sarkis cannot draw a triangle with these side lengths. Therefore, option A is correct.
Given that, a triangle with sides measuring 4 ft, 10 ft, and 16 ft.
What are the conditions to construct a triangle?
In the triangle, the sum of any two sides is always greater than the third side. The difference between any two sides of the triangle is always less than the third side.
Sarkis cannot draw a triangle with these side lengths. Therefore, option A is correct.
To learn more about triangles visit:
brainly.com/question/2773823.
#SPJ2
What happens if you try to use l' Hospital's Rule to find the limit? lim_x rightarrow infinity x/Squareroot x^2 + 3 You cannot apply l' Hospital's Rule because the function is not continuous. You cannot apply l'Hospital's Rule because the denominator equals zero for some value x = a. You cannot apply l'Hospital's Rule because the numerator equals zero for some value x = a You cannot apply l'Hospital's Rule because the function is not differentiable. Repeated applications of l'Hospital's Rule result in the original limit or the limit of the reciprocal of the function Evaluate the limit using another method.
Answers
The limit lim(x→∞) x/√(x^2 + 3) is 1, and there is no need to apply L'Hospital's Rule in this case.
When trying to use L'Hospital's Rule to find the limit lim(x→∞) x/√(x^2 + 3), it is important to note that L'Hospital's Rule can only be applied if the function is continuous and differentiable. In this case, the function is continuous and differentiable, but applying L'Hospital's Rule is not necessary as the limit can be evaluated using another method.
First, let's rewrite the given function by dividing both the numerator and the denominator by x:
lim(x→∞) (x/x) / (√(x^2 + 3)/x) = lim(x→∞) 1 / √(1 + 3/x^2)
As x approaches infinity, the term 3/x^2 approaches 0, so the limit becomes:
lim(x→∞) 1 / √(1 + 0) = 1 / √(1) = 1
Therefore, the limit lim(x→∞) x/√(x^2 + 3) is 1, and there is no need to apply L'Hospital's Rule in this case.
To know more about Limit visit:
https://brainly.com/question/12207539
#SPJ11
Find the following, rounded to the
nearest degree.
tan-1 5 =
Answers
Answer:
I believe that the answer would be 1 because after doing tan^-1 (5) i got 1.3734=1 degree
Find the ordered pair (s,t) that satisfies the system
s/2+5/t=3
3t-6s=9
Answers
The ordered pair (s,t) that satisfies the system are (1/2,4) and (1,5).
We can use the second equation to solve for one of the variables in terms of the other. Let's solve for t:
3t - 6s = 9
3t = 6s + 9
t = (2s + 3)
Now we can substitute this expression for t into the first equation and solve for s:
s/2 + 5/t = 3
s/2 + 5/(2s + 3) = 3
Multiplying both sides by the denominator (2s + 3) gives:
s(2s + 3)/2 + 5 = 3(2s + 3)
Simplifying and collecting like terms yields:
2s^2 + 3s + 10 = 6s + 9
2s^2 - 3s + 1 = 0
This quadratic equation can be factored as:
(2s - 1)(s - 1) = 0
So s = 1/2 or s = 1.
Now we can substitute these values for s into the equation we derived for t:
If s=1/2 then t=2(1/2)+3=4
If s=1 then t=2(1)+3=5
Therefore, the ordered pairs that satisfy the system are (1/2,4) and (1,5).
Know more about ordered pair here:
https://brainly.com/question/11139505
#SPJ11
Kenny has the following data:
4 1 b 4.
If the range is 6, which number could b be?
7
41
Answers
Answer:
7
Step-by-step explanation:
If range is 6 then the difference between highest and lowest is 6 so 1 + 6 = 7 so b is equal to 7.
thirteen and thirteen thousandths decimal form
Answers
I need help with this

Answers
Step-by-step explanation:
\( {17}^{2} = {8}^{2} + {b}^{2} \\ {b}^{2} = {17}^{2} - {8}^{2} \\ {b }^{2} = 225 \\ b = \sqrt{225} = 15\)
Use Pythagorean theorem
\(\\ \sf\longmapsto b^2=h^2-p^2\)
\(\\ \sf\longmapsto b^2=17^2-8^2\)
\(\\ \sf\longmapsto b^2=289-64\)
\(\\ \sf\longmapsto b^2=225\)
\(\\ \sf\longmapsto b=15ft\)
the probability that a first year student entering a certain private college needs neither a developmental math course nor a developmental english is 52% while 31% require a developmental math course and 33% require a developmental english course. find the probability that a first year student requires both a development math course and a developmental english course.
Answers
7.77% of first graders will need developmentally appropriate math and English lessons.
Probability calculations assuming that freshmen entering a private institution have a 61% chance of not needing a math development course or an English development course, compared to 21% and 37%, respectively.
Therefore, the probability is equal to 0.21 x 0.
37, representing 7.77%.
We now know that there is a 7.77% probability that new students will need developmental mathematics and English studies courses.
To know more about probability, visit,
https://brainly.com/question/13604758
#SPJ4
identify the surface whose equation is given. 6r2 + z2 = 1
Answers
The surface whose equation is given by 6r² + z² = 1 is an ellipsoid. The surface whose equation is given by 6r^2 + z^2 = 1 is a three-dimensional shape known as an ellipsoid. An ellipsoid is a type of quadric surface that is defined by three principal axes, with the lengths of these axes determined by the coefficients of the equation.
In this case, the ellipsoid has a major axis in the z-direction with a length of 1, and minor axes in the x and y directions with lengths of √(1/6). The equation can also be rewritten as (r/√(1/6))^2 + (z/1)^2 = 1, which shows that the ellipsoid is centered at the origin and has a radius of √(1/6) in the x and y directions, and a radius of 1 in the z direction.
An ellipsoid is a 3D surface that resembles an elongated sphere, with its general equation given as (x²/a²) + (y²/b²) + (z²/c²) = 1. In this case, the given equation can be rewritten in the standard form as (x²/ (1/6)) + (y²/ (1/6)) + (z²/1) = 1, which shows it's an ellipsoid.This particular ellipsoid has its major axis along the z-axis and two equal minor axes along the x and y-axes, with semi-major axis length of 1 and semi-minor axis lengths of √(1/6).
To know more about ellipsoid visit:-
https://brainly.com/question/30968823
#SPJ11
calvin had saved 550.00 he went shopping and bought 5 new cds for 19.95 each a new mp3 player for 124.99 and 6.new dvds for 12.97 each how much money does calvin now have
Answers
Answer:
249.44
Step-by-step explanation:
5 CDs each = 19.55 6 DVDs each =12.97
19.55×5 =97.75 12.97×6=77.82
mp3= 124.99
124.99+97.75+77.82=300.56
550.00-300.56=249.44
given a nonhomogeneous system of linear equa- tions, if the system is underdetermined, what are the possibilities as to the number of solutions?
Answers
If a nonhomogeneous system of linear equations is underdetermined, it can have either infinitely many solutions or no solutions.
A nonhomogeneous system of linear equations is represented by the equation Ax = b, where A is the coefficient matrix, x is the vector of unknowns, and b is the vector of constants. When the system is underdetermined, it means that there are more unknown variables than equations, resulting in an infinite number of possible solutions. In this case, there are infinitely many ways to assign values to the free variables, which leads to different solutions.
To determine if the system has a solution or infinitely many solutions, we can use techniques such as row reduction or matrix methods like the inverse or pseudoinverse. If the coefficient matrix A is full rank (i.e., all its rows are linearly independent), and the augmented matrix [A | b] also has full rank, then the system has a unique solution. However, if the rank of A is less than the rank of [A | b], the system is underdetermined and can have infinitely many solutions. This occurs when there are redundant equations or when the equations are dependent on each other, allowing for multiple valid solutions.
On the other hand, it is also possible for an underdetermined system to have no solutions. This happens when the equations are inconsistent or contradictory, leading to an impossibility of finding a solution that satisfies all the equations simultaneously. Inconsistent equations can arise when there is a contradiction between the constraints imposed by different equations, resulting in an empty solution set.
In summary, when a nonhomogeneous system of linear equations is underdetermined, it can have infinitely many solutions or no solutions at all, depending on the relationship between the equations and the number of unknowns.
To learn more about linear equations refer:
https://brainly.com/question/26310043
#SPJ11
been having this question for a while and this app wont help

Answers
The answer is B
When there is a solid point that means it is included in the graph, so you'd use a greater/less than or equal to symbol (the one with a line under). If it's an unfilled point then it means that it is not included in the graph, so you'd use a greater/less than sign.
The x² equation is less than 2 while the linear equation is greater than or equal to 2.
We know it's the x² equation that is less than two because it has a curve in it.
help me pleasee, my brain won't work

Answers
The given fractions have equal value, so Liam is correct.
How to find the equivalent fractions?Equivalent fractions are defined as fractions that have different numerators and denominators but the same value. For example, 2/4 and 3/6 are equivalent fractions because they are both equal to 1/2. A fraction is part of a whole. Equivalent fractions represent the same part of a whole.
Liam is claiming that the fraction -(5/12) is equivalent to 5/-12.
Thus, we can say that:
The fraction -(5/12) can be described as the opposite of a positive number divided by a positive number. A positive number divided by a positive number always results in a positive quotient and its' opposite is always negative.
The fraction 5/-12 can be described as a positive number divided by a negative number which always results in a negative quotient
The fractions have equal value, so Liam is correct
Read more about Equivalent fractions at: https://brainly.com/question/17220365
#SPJ1
If B=x^{2}+ 2 and C=2+2x^{2}find an expression that equals 2B+C in standard form.

Answers
The expression that equals 2B+C in standard form is 4x² + 6
How to determine the expression?From the question, we have the following parameters that can be used in our computation:
B = x² + 2
C = 2 + 2x²
The expression to calculate is given as
2B + C
Substitute the known values in the above equation, so, we have the following representation
2B + C = 2x² + 4 + 2 + 2x²
Evaluate the like terms
2B + C = 4x² + 6
Hence, the expression is 4x² + 6
Read more about expressions at
https://brainly.com/question/15775046
#SPJ1
Convert the equation –9x2 25y2 – 100y – 125 = 0 into standard form.
Answers
the standard form of the equation -9x²+25y²-100y = 125 is x²/25 + (y-2)²/9 = 1
Add 125 to both sides of the equation.
-9x²+25y²-100y = 125
Complete the square for 25y²-100y
25(y-2)²-100
Substitute 25(y-2)²-100 for 25y²-100y in the equation
-9x²+25y²-100y = 125
-9x²+25(y-2)²-100 = 125
Move −100 to the right side of the equation by adding 100 to both sides.
-9x²+25(y-2)² = 125 +100 = 225
Divide each term by 225 to make the right side equal to one.
-9x²/225 +25(y-2)²/225 = 225/225
Simplify each term in the equation in order to set the right side equal to 1. The standard form of an ellipse or hyperbola requires the right side of the equation to be 1.
x²/25 + (y-2)²/9 = 1
To know more about the standard form visit: brainly.com/question/29000730
#SPJ4
Can someone please answer this question.

Answers
Use the Pythagorean theorem to solve for the diagonal distance
Diagonal = sqrt(50^2 + 150^2)
Diagonal distance = sqrt(25,000)
Diagonal distance = 158.11 feet
Round to 158 feet.
If the stayed on the sidewalk they would walk 50 + 150 = 200 feet.
The distance they saved = 200-158 = 42 feet
Answer: 42 feet.
I sold a pencil case for $2.15.i bought it for 68 cents,what was my profit?
Answers
Answer:
1.47
Step-by-step explanation:
2.15
-0.68
borrow from the one now you have 15 minus 8 or 7next borrow from the 2 now you have 11 minus 6 or 5 then drop the one and drop the decimal hope this helped