Jenny’s home appraised for 550,000. Her asking price was 560,000 and the properties sold for 575,000. What were the new owners pay in property taxes?
Answers
Answer:
575,000
Step-by-step explanation:
The new owners pay 15000 in property taxes.
Tax rate = (Tax amount/Price before tax) × 100%
How are taxes calculated on homes?⇒ Jenny's house appraised price = 550000.
⇒The asking price was 56000.
The selling price of the property =575000
the extra amount must be paid as a tax = 575000-56000
∴ tax amouny = 15000.
The standard formula
Property tax = base value × built-up area × Age factor × type of building × category of use × floor factor.
Learn more about taxes here: https://brainly.com/question/3531009
#SPJ2
Related Questions
StartFraction 32 Over 8 EndFraction = StartFraction 28 Over x EndFraction
a.
x = 4
c.
x = 8
b.
x = 28
d.
x = 7
Answers
Answer:
d. x = 7
Step-by-step explanation:
\(\frac{32}{8} = \frac{28}{x}\)
Cross multiply, the denominator "8" is multiplied by numerator "28", while the numerator "32" is multiplied by denominator "x":
8 * 28 = 224
32 * x = 32x
\(32x = 224\)
Divide both sides by 32:
\(\frac{32}{32} = \frac{224}{32}\)
[x = 7]
Shanta's cell phone compnay charges her $45 a month plus $0.25 for each text she uses over 250. How can Shant-
represent the cost of her cell phone bill for any month assuming that she uses over 250 texts?
Answers
Answer:
45 + .25x
Step-by-step explanation:
x represents the thing that changes, assuming this is for any given month and not multiple, 45 + .25x would be the answer
In a particular year, the mean score on the ACT test was 17.2 and the standard deviation was 5.4. The mean score on the SAT mathematics test was 495 and the standard deviation was 120. The distributions of both scores were approximately bell-shaped. Round the answers to two decimal places.
Find the z-score for an ACT score of 16.
Answers
Answer:
\(X \sim N(17.2,5.4)\)
Where \(\mu=495\) and \(\sigma=120\)
And the best way to solve this problem is using the normal standard distribution and the z score given by:
\(z=\frac{x-\mu}{\sigma}\)
And replacing we got:
\( z=\frac{16-17.2}{5.4}= -0.22\)
And the answer for this case would be \(z =-0.22\)
Step-by-step explanation:
Let X the random variable that represent the scores for the SAT of a population, and for this case we know the distribution for X is given by:
\(X \sim N(17.2,5.4)\)
Where \(\mu=495\) and \(\sigma=120\)
And the best way to solve this problem is using the normal standard distribution and the z score given by:
\(z=\frac{x-\mu}{\sigma}\)
And replacing we got:
\( z=\frac{16-17.2}{5.4}= -0.22\)
And the answer for this case would be \(z =-0.22\)
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
HELP!! I will give you brainliest

Answers
I think but try it
Given that the measure of Angle CDB = 31 degrees find the indicated
measures for angle 1 and 2.

Answers
Answer:
angle 1=149°
angle 2=31°( because they are alternating angles)
Find the sums of the interior angles and the sum of the measures of the exterior angles of the polygon. Please answer 1, 2, and 3, 30 points!!!!!!!!!!!!!!!!!!!!!!!!

Answers
The sum of the internal angles of the polygons are
a) The sum is A = 540°
b) The sum is A = 360°
c) The sum is A = 1800°
What is the sum of the interior angles of a polygon?The sum of the interior angles of a polygon is given by the formula
Sum of Interior angles of a polygon with n sides is
nθ = 180° ( n - 2 )
where n is the number of sides
θ = angle in degrees
Given data ,
Let the sum of the internal angles of a polygon be represented as A
Now , the value of A is
The sum of exterior angle of n polygon is = 360°
Now ,
a)
The number of sides of the polygon = 5 sides
So , Sum of Interior angles of a polygon with n sides is
nθ = 180° ( n - 2 )
Substituting the value of n = 5 in the equation , we get
nθ = 180° ( 5 - 2 )
nθ = 180° x 3
nθ = 540°
b)
The number of sides of the polygon = 4 sides
So , Sum of Interior angles of a polygon with n sides is
nθ = 180° ( n - 2 )
Substituting the value of n = 4 in the equation , we get
nθ = 180° ( 4 - 2 )
nθ = 180° x 2
nθ = 360°
c)
The number of sides of the polygon = 12 sides
So , Sum of Interior angles of a polygon with n sides is
nθ = 180° ( n - 2 )
Substituting the value of n = 12 in the equation , we get
nθ = 180° ( 12 - 2 )
nθ = 180° x 10
nθ = 1800°
Hence , the sum of the internal angles of the polygon is solved
To learn more about sum of internal angles of polygons click :
https://brainly.com/question/14611583
#SPJ1
wo websites sell the same type of headphones.
Website A
Website B
Cost of headphones
£49.95
£47.68
Cost of postage
£4.39
£6.95
Including the cost of postage which website is cheaper and by how much
Answers
Answer:
A CHEAPER
Step-by-step explanation:
49.95+4.39=54.34
47.68+6.95=54.63
A) 54.34<54.63 B)
: What would be another way to calculate total interest rather than just adding up the individual interest amounts?
Answers
Answer:
Step-by-step explanation:
At the end of the loan/investment, you can take the accumulated value and subtract that from the principle/PV to get the total interest
The total interest earned can be determined by subtracting the principal from the future value of the loan.
There are two types of interests : simple interest and compound interest.
Compound interest is a type of interest in which the principal and interest already accumulated also earn an interest. While for simple interest it is only the principal that earns interest.
For example, if a loan of $4000 earns 10% interest compounded yearly, the future value of the the amount in 5 years is:
$4000 x (1.1)^5 = 6442.04
The interest earned over the 5 years can be determined by subtracting the cost of the loan from the future value of the investment
Interest = 6442.04 - $4000 = $2442.04
Another example, if a loan of $4000 earns 10% simple interest, the interest of the loan after 5 years is:
$4000 x 0.1 x 5 = $2000
To learn more about interest, please check: brainly.com/question/9352088?referrer=searchResults
Find the limit of the difference quotients for f(x) = x2+2x+1 if a= -1
Answers
The limit of the difference quotients for f(x) = x^2 + 2x + 1 as x approaches -1 is indeterminate.
To find the limit of the difference quotients for the function f(x) = x^2 + 2x + 1 as x approaches -1, we need to evaluate the following expression:
lim(x→-1) [f(x) - f(-1)] / (x - (-1))
First, let's substitute the values into the expression:
lim(x→-1) \([(x^2 + 2x + 1) - (-1^2 + 2(-1) + 1)] / (x + 1)\)
Simplifying further:
lim(x→-1) \([(x^2 + 2x + 1) - (1 - 2 + 1)] / (x + 1)\)
lim(x→-1)\([x^2 + 2x + 1 - 0] / (x + 1)\)
lim(x→-1) \((x^2 + 2x + 1) / (x + 1)\)
Now, we can directly substitute x = -1 into the expression:
\((-1^2 + 2(-1) + 1) / (-1 + 1)\)
(1 - 2 + 1) / (0)
0 / 0
We have obtained an indeterminate form of 0/0. This indicates that we need to further simplify the expression or use other techniques, such as L'Hôpital's rule, to evaluate the limit. However, without additional information or simplification, we cannot determine the precise value of the limit at x = -1.
For more such information on: quotients
https://brainly.com/question/11418015
#SPJ8
With a mean of 100 and standard deviation of 15, what percentage of IQ scores are less than 110
Answers
Answer:
i think 125
Step-by-step explanation:
What is the value of the expression below when x=5?

Answers
Answer:
790
Step-by-step explanation:
You put 5 instead of x and you calculat
6*5^3 +8*5= 750+40=790
PLEASE HELP TODAY!!!! WILL GIVE BRAINLIST

Answers
Hello!
We will go tu use the pythagorean theorem!
So:
BA² = BC² + AC²
AC² = BA² - BC²
AC² = 52² - 20²
AC² = 2304
AC = √2304
AC = 48
What is an equation of the line that passes through the points (-5, 0) and
(-2, -3)?
Answers
Answer:
The equation is y = -x - 5.
Step-by-step explanation:
First find the slope by doing -3-0 over -2 - (-5) which can be simplified to -3-0 over -2+5. You'll get -3/3 which equals -1. Then, use slope intercept form which is y = mx + b. Substitute your values. X = -2, Y = -3, and M = -1. After substituting your values, your equation should look like this: -3 = -2(-1) + b. Your solving for b. -2 x -1 = 2. -3 = 2 + b. -3 - 2 = -5. B = -5. In the end, your equation should be y = -1x - 5.
Which of these must be true

Answers
because they are both the radius of the circles and their central angles are also congruent.
Round 14,456 to nearest ten
Answers
Answer:
14,460.
Step-by-step explanation:
14,456 up by 4. anything 6 or above goes up. the tenth place is the second to last number.
Write the decimal for each word. Then round the answer to the nearest tenthc) nine hundred forty-two ten-thousandths
Answers
nine hundred forty-two ten-thousandths:
1. Write the first part as a number: nine hundred forty-two
nine hundred: 900
forty-two: 42
900+42= 942
2. Identify the position of number above in the decimal knowing that ten-thousandths ends in 4 disgits after the decimal point (the last digit of number above needs to be in the ten-thousandths position):
The given number is: 0.0942Rounded the answer to the nearest tenth: 0.1Venera sent a chain letter to her friends, asking them to forward the letter to more friends.
The relationship between the elapsed time t, in months, since Venera sent the letter, and the number of
people, P(t), who receive the email is modeled by the following function:
3t+7
P(t) = 2
Complete the following sentence about the monthly rate of change in the number of people who receive
the email.
Round your answer to two decimal places.
Every month, the number of people who receive the email is multiplied by a factor of
Answers
Answer:
It is multiplied by a factor of 8
Step-by-step explanation:
Every month, the number of people who receive the email is multiplied by a factor of 8.
What is an exponent?Let b is the base and x is the power of the exponent function and a is the leading coefficient. The exponent is given as
y = a(b)ˣ
Venera sent a chain letter to her friends, asking them to forward the letter to more friends.
The relationship between the elapsed time t, in months, since Venera sent the letter, and the number of people, P(t), who receive the email is modeled by the following function:
\(\rm P(t) = 2^{3t+7}\)
Every month, the number of people who receive the email is multiplied by a factor will be
For t = 2, we have
P(2) = 2³⁽²⁾⁺⁷
P(2) = 2¹³
For t = 3, we have
P(3) = 2³⁽³⁾⁺⁷
P(3) = 2¹⁶
Then the factor will be
⇒ P(3) / P(2)
⇒ 2¹⁶ / 2¹³
⇒ 2³
⇒ 8
More about the exponent link is given below.
https://brainly.com/question/5497425
#SPJ2
Faith is working two summer jobs, making $13 per hour lifeguarding and $12 per hour washing cars. Last week Faith worked a total of 12 hours and earned a total of $150. Write a system of equations that could be used to determine the number of hours Faith worked lifeguarding last week (x) and the number of hours she worked washing cars last week (y).
Answers
if she worked "x" hours lifeguarding at $13 per hour, that means she earned a total of 13*x or 13x, if she worked washing cars for "y" hours at $12 per hour that means she made on those hours 12*y or 12y, and we know that whatever their sum combined is a grand total of $150.
Last week she worked a total of 12 hours doing both, namely x + y = 12.
\(\begin{cases} 13x+12y &= 150\\ x + y &= 12 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{using the 2nd equation}}{x +y = 12}\implies y = 12 -x \\\\\\ \stackrel{\textit{substituting on the 1st equation}}{13x+12(12-x) = 150}\implies 13x+144-12x = 150\implies x + 144 = 150 \\\\\\ \boxed{x = 6}~\hfill \stackrel{\textit{we know that}}{y = 12 -x}\implies \boxed{y = 6}\)
solve simultaneously 2x - y = - 10 and 3x + 2y = - 1
Answers
The solution to the system of equations is x = -3 and y = -4.
To solve the system of equations:
Equation 1: 2x - y = -10
Equation 2: 3x + 2y = -1
We can use the method of substitution or elimination to find the values of x and y.
Let's use the method of elimination:
Multiply Equation 1 by 2 to make the coefficients of y in both equations equal:
2(2x - y) = 2(-10)
4x - 2y = -20
Now, we can eliminate y by adding Equation 2 and the modified Equation 1:
(3x + 2y) + (4x - 2y) = -1 + (-20)
7x = -21
x = -3
Substitute the value of x into Equation 1 to solve for y:
2(-3) - y = -10
-6 - y = -10
y = -10 + 6
y = -4
Therefore, the solution to the system of equations is x = -3 and y = -4.
for such more question on equations
https://brainly.com/question/17482667
#SPJ8
A carpenter is making doors that are 20582058 millimeters tall. If the doors are too long they must be trimmed, and if they are too short they cannot be used. A sample of 1010 doors is made, and it is found that they have a mean of 20462046 millimeters with a standard deviation of 1515. Is there evidence at the 0.050.05 level that the doors are too short and unusable
Answers
Answer:
Z= 0.253
Z∝/2 = ± 1.96
Step-by-step explanation:
Formulate the null and alternative hypotheses as
H0 : u1= u2 against Ha : u1≠ u2 This is a two sided test
Here ∝= 0.005
For alpha by 2 for a two tailed test Z∝/2 = ± 1.96
Standard deviation = s= 15
n= 10
The test statistic used here is
Z = x- x`/ s/√n
Z= 2058- 2046 / 15 / √10
Z= 0.253
Since the calculated value of Z= 0.253 falls in the critical region we reject the null hypothesis.
There is evidence at the 0.05 level that the doors are too short and unusable.
Find the surface area

Answers
Answer: 120 yds
Step-by-step explanation:
48+30+24+18+120 yds
A cake pan in the shape of a right triangle is shown below. What is the volume of the open area of the cake pan? A. 90 cubic inches B. 45 cubic inches C. 120 cubic inches D. 180 cubic inches
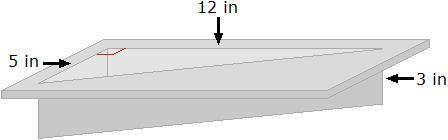
Answers
Answer:
Im pretty sure its d
Step-by-step explanation:
im not sure but i’m sorry if its wrong
Answer:
D. 180
Step-by-step explanation: multiply
What is the measure of angle DEC?

Answers
Answer:
95
Step-by-step explanation:
dct equals 140, dct also equal det plus edc, so 140 - 45 = 95
Here are the shopping times (in minutes) of ten shoppers at a local grocery store.
Complete the grouped frequency distribution for the data.
In the distribution, the frequency of a class is the number of shopping times in that class.
(Note that we are using a class width of 5.)

Answers
The frequency which is to filled in the table is 1, 4, 2 and 4.
Given that;
All shopping time of ten shopkeeper:
25, 29, 25, 18, 24, 28, 36, 25, 33, 37
We have to complete the frequency in the table. Frequency of something is the number of times that number is coming.
Since, Shopping time is given as ,
25, 29, 25, 18, 24, 28, 36, 25, 33, 37
And, Intervals for which frequency is given is ,
18 to 22, 23 to 27, 28 to 32, 33 to 37.
Hence, WE get;
Numbers in the range 18 to 22 = 18 therefore 1
Numbers in the range 23 to 27 = 25, 25, 24, 25 therefore 4
Numbers in the range 28 to 32 = 29, 28 therefore 2
Numbers in the range 33 to 37 = 36, 33, 37, therefore 3
Hence, the frequency which is to filled are 1, 4, 2 and 4.
Learn more about frequency visit:
brainly.com/question/254161
#SPJ1
2. Kasie lives in Seattle. She can see her house from the observation deck of the Seattle Space Needle. The
observation deck is 520 feet above the ground and the angle of depression from the deck to her house
is 70. What is the direct distance from the base of the Space Needle to Kasie's house? Round your
answer to the nearest foot.
Answers
Direct distance from the base of the Space Needle to Kasie's house = 1429 feet.
What is angle of depression?The angle of depression is the angle between the horizontal line and the observation of the object from the horizontal line. It is basically used to get the distance of the two objects where the angles and an object's distance from the ground are known to us.
Given,
Height of the observation deck AB = 520 feet
Angle of depression = 70°
Distance of the Space needle base to house BC = ?
By the figure,
tan70° = AB/BC
BC = tan70°(AB)
BC = 2.7475(520)
BC = 1428.7 feet
Distance of the Space needle base to house to nearest foot = 1429 feet
Hence, 1429 feet is the distance between base of the Space Needle to Kasie's house.
Learn more about angle of depression here:
https://brainly.com/question/13514202
#SPJ1

question 6: use an eigenbasis to determine a matrix consider an matrix such that is an eigenvector of with eigenvalue and is an eigenvector of with eigenvalue . determine .
Answers
since is an eigenvector of with eigenvalue , we can express the second column of the matrix as . So the matrix is given by:
\($$\begin{bmatrix}\lambda_1 & 0 \\0 & \lambda_2\end{bmatrix}$$\)
This matrix is a diagonal matrix, which is a matrix with all entries except for those on the main diagonal set to zero. In this matrix, the main diagonal elements, which are the elements on the diagonal from the upper left to the lower right, are labelled \(\lambda_1$ and $\lambda_2\)This matrix is symmetric, meaning that the transpose of the matrix is equal to the original matrix. The matrix represents a linear transformation in which the eigenvalues \(\lambda_1$ and $\lambda_2\) represent the scalar factors by which the vectors in the transformed space are scaled. The eigenvalues of this matrix can be used to determine the magnitude of the transformation it performs.
The eigenvalues of this matrix can be calculated by solving the equation
\(\det(\mathbf{A} - \lambda \mathbf{I}) = 0\)
where \(\mathbf{A}\) is the matrix and \(\mathbf{I}\) is the identity matrix.
In this case, we have
\($\det\begin{bmatrix}\lambda_1 - \lambda & 0 \\0 & \lambda_2 - \lambda\end{bmatrix}\)
=\((\lambda_1 - \lambda)(\lambda_2 - \lambda)\) = 0.
Solving this equation for \(\lambda$, we get $\lambda = \lambda_1\) and \(\lambda = \lambda_2\)Therefore, the eigenvalues of this matrix are \(\lambda_1 and \lambda_2\)
the complete question is : use an eigenbasis to determine a matrix consider an matrix such that is an eigenvector of with eigenvalue and is an eigenvector of with eigenvalue . determine the Given an matrix such that is an eigenvector of with eigenvalue and is an eigenvector of with eigenvalue , what is the matrix.
Learn more about matrix here
https://brainly.com/question/29132693
#SPJ4
Please help please help!!!!!!
A,B,C,or ,D???

Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\( {5}^{ {3}^{5} } = {5}^{3 \times 5} = {5}^{15} \)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Thus the correct answer is (( B )) .
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Evaluate the expression below when x = 6 and y = 2. 6x2y3
Answers
Answer:
I think that the answer is 432.
Step-by-step explanation:
6x2y3.We have x as 6 and y as 2.So we replace them with their numbers.
We'll have 6*6*2*2*3 which will give us 432. I HOPE THIS HELPS.
This equation shows a way to find 20/32 (equation is 20/32=20/32÷1=20/32÷?/?=?/8) enter your answer in the boxes below