Jan's pay is in direct variation to the hours she works. Jan earns $54 for 12 hrs of work. How much will she earn for 18 hrs of work?
Answers
Answer:
if she works 18 she earns 81 dollars i think
Related Questions
PLSSS HELP IF YOU TULRY KNOW THISSSS

Answers
Answer: The answer is 7
Step-by-step explanation:
Answer: x = 7
Step-by-step explanation:
Subtract 7 on each side to isolate X
7 + x = 14
-7 -7
x = 7
Please help me im fr struggling rn...

Answers
Answer:
I believe it would be D, the smiley face that's on the bottom.
Step-by-step explanation:
Since the smiley face is first reflected on the y axis, (vertically,) it'd be upside down. Then, turning it 90 degrees clockwise is simply just turning it left once.
what would be 8/1 x 1/2
Answers
Answer:
4.
Step-by-step explanation:
8*1 / 1*2
= 8/2
= 4.
\(8\times \dfrac 12 = 4\)
Select the correct answer below: -[infinity] O 0 2 516 -5x² - 5x+7 lim x-[infinity] -6x³ - 4x² + 6x - 7 QUESTION 7. 1 POINT The rate in which the balance of an account that is increasing is given by A'(t)=375e^(0.025t). (the 0.025t is the exponent on the number e) If there was $18,784.84 dollars in the account after it has been left there for 9 years, what was the original investment? Round your answer to the nearest whole dollar. Select the correct answer below: O $14,000 O $14,500 O $15,000 O $15,500
Answers
The original investment in the account is $15,000. To find the original investment, we need to integrate the rate of change function A'(t) to get the accumulated balance function A(t).
Then we can solve for the original investment by setting A(t) equal to the final balance and solving for t.
Integrating A'(t) = 375e^(0.025t) with respect to t gives:
A(t) = ∫375e^(0.025t) dt
Using the integration rule for e^x, we have:
A(t) = 375(1/0.025)e^(0.025t) + C
Given that the final balance A(t) after 9 years is $18,784.84, we can set up the equation:
18,784.84 = 375(1/0.025)e^(0.025*9) + C
Simplifying the equation, we find:
18,784.84 = 15,000e^(0.225) + C
Solving for C, we have:
C = 18,784.84 - 15,000e^(0.225)
Substituting C back into the accumulated balance equation, we get:
A(t) = 375(1/0.025)e^(0.025t) + (18,784.84 - 15,000e^(0.225))
To find the original investment, we set A(t) equal to the initial balance:
A(t) = P
Solving for P, we find:
P = 375(1/0.025)e^(0.025t) + (18,784.84 - 15,000e^(0.225))
Plugging in t = 0, we can evaluate P:
P = 375(1/0.025)e^(0.025*0) + (18,784.84 - 15,000e^(0.225))
P ≈ $15,000
Therefore, the original investment in the account was approximately $15,000.
To learn more about integration rule click here: brainly.com/question/32525685
#SPJ11
If f(x)=ln(x+4+e^(-3x)), then f '(0) =
Answers
If derivative of \(f(x)=ln(x+4+e^{(-3x)})\), then f '(0) = -2/5.
What is derivative?
In calculus, the derivative of a function is a measure of how the function changes as its input changes. More specifically, the derivative of a function at a certain point is the instantaneous rate of change of the function at that point.
To find f'(0), we first need to find the derivative of f(x) with respect to x. Using the chain rule, we get:
\(f'(x) = 1 / (x+4+e^{(-3x)}) * (1 - 3e^{(-3x)})\)
Now we can find f'(0) by substituting the value x=0:
\(f'(0) = 1 / (0+4+e^{(-3(0))}) * (1 - 3e^{(-3(0))})\)
f'(0) = 1 / (4+1) * (1 - 3)
f'(0) = -2/5
Therefore, f'(0) = -2/5.
To learn more about derivative visit:
https://brainly.com/question/23819325
#SPJ4
Which elephants weight is 2.85 tons when rounded to the nearest hundred
Answers
HELP PLEASE
(-4)-(-2)-{(-5)-[(-7)+(-3)-(-8)]}
Answers
Answer:
answer is 1
Step-by-step explanation:
Answer:
(-4)-(-2)-{(-5)-[(-7)+(-3)-(-8)]}
=-4+2-{-5-[-7-3+8]
=2-{-5-[-2]}
=2-{-5+2}
=2+3
=5
Step-by-step explanation:
If a discrete random variable X follows hypergeometric distribution, with m=7,n=5,k=6. What is P(X=5)? a. dhyper(5,7,5,6) b. phyper(5,7,5,6) c. phyper(4,7,5,6) d. dbinom(5,7,5,6) e. pbinom(4,7,5,6)
Answers
The probability of a discrete random variable X following a hypergeometric distribution, with m=7, n=5, and k=6, to have a value of 5 is dhyper(5,7,5,6).
Hypergeometric distributions are used to calculate the probability of success in an independent sample drawn from a finite population without replacement. The probability of success is given by the equation: dhyper(x, m, n, k), where x is the number of successes, m is the population size, n is the number of draws, and k is the number of successes in the population.
In this case, x = 5, m = 7, n = 5, and k = 6. Therefore, the probability of success for X = 5 is dhyper(5,7,5,6).
For more information about probability, visit:
https://brainly.com/question/13604758
#SPJ11
suppose that an individual has a body fat percentage of 14.4% and weighs 128 pounds. How many pounds of his weight is made up of fat? round your answer to the nearest tenth.
Answers
Is the function F(x)=5x2
Answers
I don’t get this please example

Answers
All angles in a triangle must add up to 180 degrees. The missing angle in the triangle is 34 degrees. We can then subtract 34 from 180 to find x because a straight line is 180 degrees. 180 - 34 = 146. x = 146 degrees.
find theta if cos=-0.9659
Answers
Answer:
Theta = 346.44 degrees
Step-by-step explanation:
If cos(theta) = -0.9659, we can use the inverse cosine function (cos^-1) to find theta. Here's how we can solve it:
cos(theta) = -0.9659
cos^-1(cos(theta)) = cos^-1(-0.9659) [applying cos^-1 to both sides]
theta = 2π - cos^-1(0.9659) [using the fact that cos(theta) is negative in the third quadrant]
Using a calculator, we can evaluate cos^-1(0.9659) as 15.56 degrees (rounded to two decimal places). Therefore:
theta = 2π - 15.56 degrees
theta = 346.44 degrees
So, theta is 346.44 degree.
In phase 2 of a three-phase clinical trial to test the efficacy of the BNT163b2 mRNA vaccine for COVID-19, participants were randomly assigned to receive either the vaccine or a placebo. In the placebo group, 18,325 participants with no evidence of infection received placebo injections and 162 eventually contracted COVID-19. Of the 18,198 participants with no evidence of infection who received the vaccine, 8 eventually contracted COVID-19. Conventional wisdom suggested that the infection rate for COVID-19 was about 3%. Assume that the 18,325 people who received the placebo represent a simple random sample of all people with no prior evidence of infection and have not been vaccinated. Let's say you carry out a hypothesis test of significance to determine if there is evidence from this sample that the proportion of unvaccinated people who catch the virus is not 0.03. Compute the one-sample z- statistic. Give your answer to at least one decimal place.
Answers
The one-sample z-statistic for evaluating the hypothesis that unvaccinated people get COVID-19 is not 0.03 is -85.7. This statistic tested the hypothesis that unvaccinated people do not get COVID-19 at 0.03%.
In order to compute the one-sample z-statistic, we must first do a comparison between the observed proportion of COVID-19 instances in the placebo group and the expected proportion of 0.03. (p - p0) / [(p0(1-p0)) / n is the formula for the one-sample z-statistic. In this formula, p represents the actual proportion, p0 represents the predicted proportion, and n represents the sample size.
The observed proportion of COVID-19 instances among those who received the placebo is 162/18325 less than 0.0088. According to the received wisdom, the proportion that should be anticipated is 0.03. The total number of people sampled is 18325. After entering these numbers into the formula, we receive the following results:
z = (0.0088 - 0.03) / √[(0.03(1-0.03)) / 18325] ≈ (-0.0212) / √[(0.0291) / 18325] ≈ -85.7
As a result, the value of the z-statistic for just one sample is about -85.7. This demonstrates that the observed proportion of COVID-19 cases in the unvaccinated population is significantly different from the expected proportion of COVID-19 cases in that population.
Learn more about z-statistic here:
https://brainly.com/question/30904553
#SPJ11
straight line graphs: find the equation of the lines shown

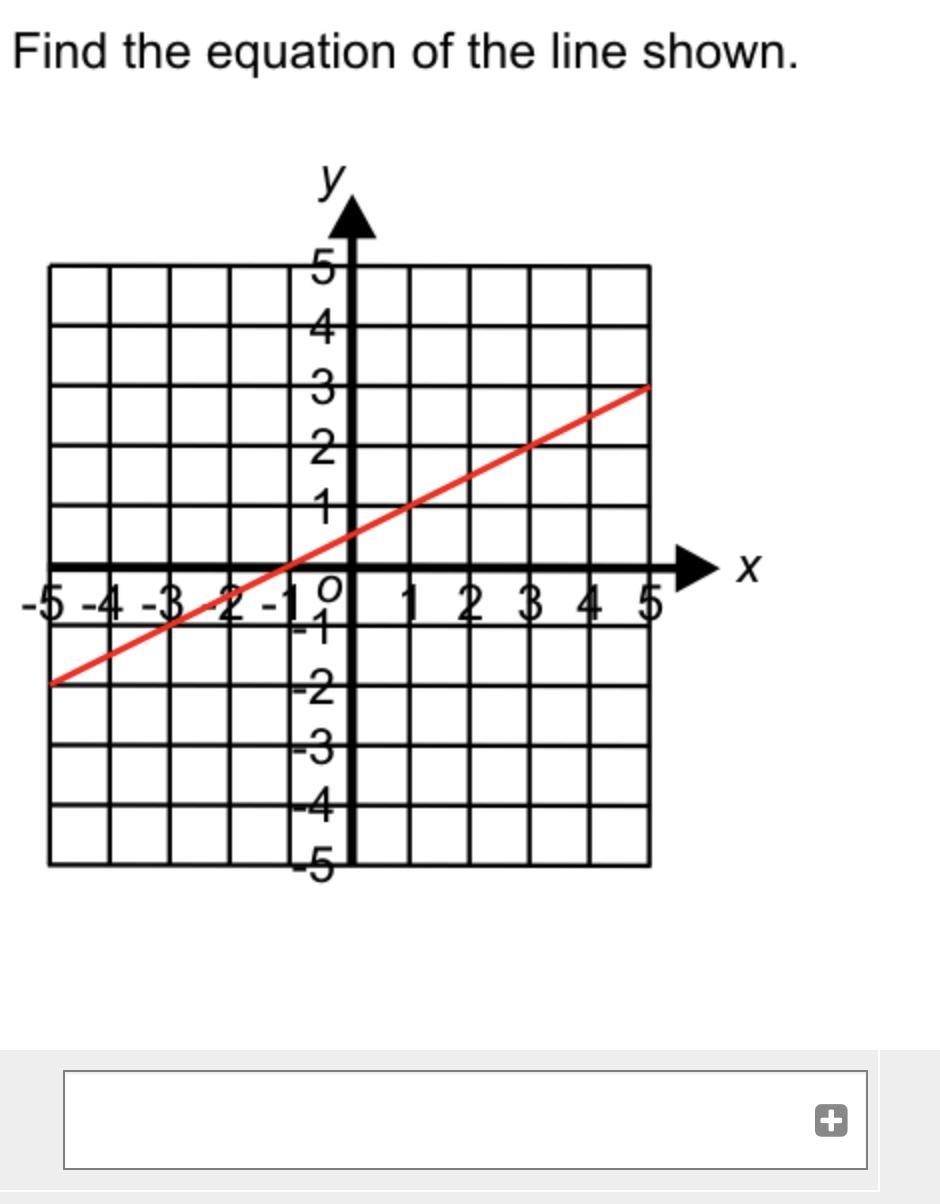
Answers
Answer:
1. y = -2n + 9
2. y = (1/2)x + 1/2
Step-by-step explanation:
1.
The equation of a line is denoted by y = mx + b, where m is the slope and b is the y-intercept.
Slope is calculated by taking two coordinates and dividing the difference of the y-coordinates by the difference of the x-coordinates. The y-intercept is where the line intersects the y-axis.
Let's choose any two points on the line: (4, 1) and (3, 3). Then:
slope = m = (3 - 1) / (3 - 4) = 2 / (-1) = -2
Now, we can also see that at the point (0, 9), the line intersects the y-axis, so that means b = 9.
The equation is thus y = -2n + 9.
2.
Let's again choose any two points to find the slope: (1, 1) and (3, 2). Then:
slope = m = (2 - 1) / (3 - 1) = 1/2
We can see that the line crosses the y-axis at the point (0, 1/2), so that means b = 1/2.
The equation is thus y = (1/2)x + 1/2.
~ an aesthetics lover
Answer:
1. y = -2x + 9
2. y = (1/2)x + 1/2
Step-by-step explanation:
There was a mistake on the last one so I would like to correct it it is
y= -2x+9
The other one said -2n its -2x
A team has probability 2/3 of winning whenever it plays. Find each of the following probabilities that the team will win. a). At most 4 out of 5 games. b). At most 4 out of 5 games, given that it has won already the first 3 games of a 5-game series.
Answers
The probability that the team will win at most 4 out of 5 games is 8/9.
To calculate the probability of winning at most 4 out of 5 games, we need to find the probability of winning 0, 1, 2, 3, or 4 games.
The probability of winning exactly k games out of 5 is given by the binomial distribution formula:
P(X = k) = (5 choose k) * (2/3)^k * (1/3)^(5-k)
Where "n choose k" is the binomial coefficient, representing the number of ways to choose k items from a set of n items. In this case, it represents the number of ways to win k games out of 5.
Using this formula, we can calculate the individual probabilities:
P(X = 0) = (5 choose 0) * (2/3)^0 * (1/3)^5 = (1) * (1) * (1/243) = 1/243
P(X = 1) = (5 choose 1) * (2/3)^1 * (1/3)^4 = (5) * (2/3) * (1/81) = 10/243
P(X = 2) = (5 choose 2) * (2/3)^2 * (1/3)^3 = (10) * (4/9) * (1/27) = 40/243
P(X = 3) = (5 choose 3) * (2/3)^3 * (1/3)^2 = (10) * (8/27) * (1/9) = 80/243
P(X = 4) = (5 choose 4) * (2/3)^4 * (1/3)^1 = (5) * (16/81) * (1/3) = 80/243
To find the probability of winning at most 4 out of 5 games, we sum up these probabilities:
P(X <= 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = (1/243) + (10/243) + (40/243) + (80/243) + (80/243) = 8/9.
To know more about the binomial distribution, refer here:
https://brainly.com/question/29137961#
#SPJ11
If we are told that ab= 0, then what can we infer by the zero product property we know =0 or. =0
Answers
When ab = 0, the zero-product property tells us that at least one of the factors (a or b) must be zero in order for the equation to hold true.
We are given that ab = 0, where a and b are variables or numbers.
According to the zero-product property, if the product of two factors is equal to zero, then at least one of the factors must be zero.
In our case, we have ab = 0. This means that the product of a and b is equal to zero.
To satisfy the condition ab = 0, at least one of the factors (a or b) must be zero. If either a or b is zero, then when multiplied with the other factor, the product will be zero.
It is also possible for both a and b to be zero, as anything multiplied by zero gives zero.
Therefore, based on the zero-product property, we can infer that either a = 0 or b = 0 when ab = 0.
In summary, when ab = 0, the zero-product property tells us that at least one of the factors (a or b) must be zero in order for the equation to hold true.
Learn more about property from
https://brainly.com/question/2807928
#SPJ11
Find the standard deviation of the data set shown. Round your answer to the nearest tenth.
4,5,9,1,2,5
The standard deviation is about_________
Answers
Mark Brainliest Please
Answer:
Answer is gicen in the image attached.
Step-by-step explanation:
Standard deviation (SD) measured the volatility or variability across a set of data. It is the measure of the spread of numbers in a data set from its mean value and can be represented using the sigma symbol (σ). The following algorithmic calculation tool makes it easy to quickly discover the mean, variance & SD of a data set.
For more help check Khan academy video
https://www.khanacademy.org/math/statistics-probability/displaying-describing-data/sample-standard-deviation/v/sample-standard-deviation-and-bias

Answer:
2.6
Step-by-step explanation:
To calculate standard deviation:
(1) Find the mean - 4.33
4 + 5 + 9 + 1 + 2 + 5 = 26 26 / 6 = 4.333... ≈ 4.33
(2) Subtract the mean from each value and square each result
\((4 - 4.33)^2 = 0.1089\) \((5 - 4.33)^2 = 0.4489\) \((9 - 4.33)^2 = 21.8089\)
\((1 - 4.33)^2 = 11.0889\) \((2 - 4.33)^2 = 5.4289\) \((5 - 4.33)^2 = 0.4489\)
(3) Find a new mean with the new values from the previous step
0.1089 + 0.4489 + 21.8089 + 11.0889 + 5.4289 + 0.4489 = 39.3334
39.3334 / 6 = 6.555566667
(4) Take the square root of the new mean.
\(\sqrt[]{x6.555566667} =2.560384086\)
2.560384086 rounded to the nearest tenth is: 2.6
Easy question!!! 1. Which statement is true?
All quadrilaterals are rectangles.
All quadrilaterals are squares.
All rectangles are quadrilaterals.
All quadrilaterals are parallelograms.

Answers
Answer:
All quadrilaterals are squares. All rectangles are quadrilaterals.
All quadrilaterals are parallelograms.
Step-by-step explanation:
100bbl/ day of oil is flowing in a 2 inch inner diameter wellbore with pipe relative roughness of 0.001. The oil has density of 48lbm/ft 3 and viscosity of 1.8cp. The wellbore is deviated 15 degrees from horizontal flow and has length of 6,000ft. The bottom hole flowing wellbore pressure is 2,200psi.
a) Obtain the potential pressure drop in the wellbore (psi).
b) Determine the frictional pressure drop in the wellbore (psi).
c) If there is also gas flowing in the wellbore at 150ft 3 / day covering 20% of the total pipe volume, calculate the in-situ oil velocity (ft/s).
d) For case (c), determine the flow regime of the two-phase flow.
Answers
a) To obtain the potential pressure drop in the wellbore, we can use the hydrostatic pressure equation.
The potential pressure drop is equal to the pressure gradient multiplied by the length of the wellbore. The pressure gradient can be calculated using the equation: Pressure gradient = (density of oil × acceleration due to gravity) × sin(θ), where θ is the deviation angle of the wellbore from horizontal flow. In this case, the pressure gradient would be (48 lbm/ft^3 × 32.2 ft/s^2) × sin(15°). Multiplying the pressure gradient by the wellbore length of 6,000 ft gives the potential pressure drop.
b) To determine the frictional pressure drop in the wellbore, we can use the Darcy-Weisbach equation. The Darcy-Weisbach equation states that the pressure drop is equal to the friction factor multiplied by the pipe length, density, squared velocity, and divided by the pipe diameter. However, to calculate the friction factor, we need the Reynolds number. The Reynolds number can be calculated as (density × velocity × diameter) divided by the oil viscosity. Once the Reynolds number is known, the friction factor can be determined. Finally, using the friction factor, we can calculate the frictional pressure drop.
c) To calculate the in-situ oil velocity, we need to consider the total volume of the pipe, including both oil and gas. The total pipe volume is calculated as the pipe cross-sectional area multiplied by the wellbore length. Subtracting the gas volume from the total volume gives the oil volume. Dividing the oil volume by the total time taken by the oil to flow through the pipe (converted to seconds) gives the average oil velocity.
d) The flow regime of the two-phase flow can be determined based on the oil and gas mixture properties and flow conditions. Common flow regimes include bubble flow, slug flow, annular flow, and mist flow. These regimes are characterized by different distribution and interaction of the oil and gas phases. To determine the specific flow regime, various parameters such as gas and liquid velocities, mixture density, viscosity, and surface tension need to be considered. Additional information would be required to accurately determine the flow regime in this scenario.
Learn more about viscosity here: brainly.com/question/14004181
#SPJ11
The ordered pairs below represent a relation between x and y.
(-3,0), (-2,4), (-1,8), (0,12), (1,16), (2,20)
Could this set of ordered pairs have been generated by a linear function?

Answers
Yes, this set of ordered pairs has been generated by a linear function because the relative difference between y-values and x-values is the same no matter which pairs of (x, y) values you use to calculate it.
We have given that,
The ordered pairs below represent a relation between x and y.
(-3,0), (-2,4), (-1,8), (0,12), (1,16), (2,20)
What is a graph?The graph is a mathematical representation of a network and it describes the relationship between lines and points.
Given are ordered pairs are: (-3,0) (-2,4)(-1,8)(0,12)(1,16)(2,20).
It can be seen that there is only a unit increase in x coordinates and a unit increase in consecutive y- coordinates.
Now, if we set up the equation of line as
Here, m =4 and b = 12
So the relationship is linear and represented by the equation
y=4x+12
Hence, the relative difference between y-values and x-values is the same no matter which pairs of (x, y) values you use to calculate it.
The correct option is (B)
Read more on Brainly.com
https://brainly.com/question/8975999
#SPJ1
X + 3y + 12
Y= -2/3x + 10
X=?
Y=?
Answers
Answer:
\(y = \frac{2}{3} \)
\(x = 14\)
Step-by-step explanation:
I added a photo of my solution (I assume you made a mistake in the exercise, because it had to be x = 3y + 12, or maybe I'm wrong...)

How do I solve... a for this equation? What steps should I take to solve it?
2B(F+a)=H
Answers
(F + a) = H/2B
Now all you have to do is subtract F from both sides to get:
a = H/2B - F
find an equation of the plane through the point and perpendicular to the line
Answers
To find an equation of a plane through a given point and perpendicular to a given line, you can follow these steps:
1. Find the direction vector of the given line. This can be done by subtracting the coordinates of any two points on the line. Let's denote this vector as "d".
2. Find the normal vector of the plane. Since the plane is perpendicular to the line, its normal vector will be the same as the direction vector of the line. So, the normal vector of the plane is "d".
3. Use the coordinates of the given point on the plane to find the equation of the plane. Let's denote the coordinates of the point as (x₀, y₀, z₀).
The equation of the plane can be written as:
Ax + By + Cz = D,
where A, B, C are the components of the normal vector "d", and x, y, z are the variables representing any point on the plane.
To find the values of A, B, C, and D, substitute the coordinates of the given point into the equation:
A(x₀) + B(y₀) + C(z₀) = D.
Therefore, the equation of the plane through the given point and perpendicular to the line is:
d₁(x - x₀) + d₂(y - y₀) + d₃(z - z₀) = 0,
where (d₁, d₂, d₃) are the components of the direction vector "d" of the line, and (x₀, y₀, z₀) are the coordinates of the given point.
to know more about perpendicular here:
brainly.com/question/12746252
#SPJ11
Find the equation of the plane passing through the point (−1,3,2) and perpendicular to each of the planes x+2y+3z=5 and 3x+3y+z=0.
f(x) = 12x + 10 is a function which can used to to calculate a person's daily paycheck.
Which would be a reasonable domain for this function?
A : all real numbers
B : 0
C : 0
D : 0
Answers
A : all real numbers
Answer:
A. All real numbers.
Step-by-step explanation:
Craig has 72 feet of material to build a fence around a rectangular flower bed on his property. if the width of the fence must be 3 feet, what is the length of the fence in yards if he uses all 72 feet of material? 11 yards 33 yards 66 yards 22 yards
Answers
The length of the fence in feet if he uses all 72 feet of material is 33 feet.
Perimeter of a rectangleWidth of the fence = 3 feetPerimeter = 72 feetLength = xPerimeter = 2(length + width)
72 = 2(x + 3)
72 = 2x + 6
72 - 6 = 2x
68 = 2x
x = 68/2
x = 33 feet
Therefore, the length of the fence in feet if he uses all 72 feet of material is 33 feet.
Learn more about perimeter of rectangle:
https://brainly.com/question/17297081
#SPJ4
Copy and complete the statement for ΔDEF with medians DH, EJ, and FG, and centroid K. DK = _ KH
Answers
The centroid is the point of intersection of the medians. In triangle ΔDEF, the statement DK = 2KH holds true.
DK = 2KH
In triangle ΔDEF, the statement DK = 2KH means that the length of DK is twice the length of KH. Let's understand this statement with an example.
Suppose we have a triangle ΔDEF, with medians DH, EJ, and FG, and centroid K. If we measure the length of KH and find it to be 5 units, then according to the statement DK = 2KH, the length of DK would be 2 times 5, which is 10 units.
This implies that the distance from the centroid K to a vertex D is twice the distance from the centroid K to the midpoint of the side opposite to D. In our example, the distance from K to D is twice the distance from K to the midpoint of the side opposite to D, which is 10 units and 5 units, respectively.
This relationship holds true for any triangle, regardless of its size or shape. The medians always intersect at the centroid, and the ratio of the lengths DK to KH is always 2:1.
Learn more about medians here:
https://brainly.com/question/300591
#SPJ11
Calculus. Find the area.

Answers
Answer:
8/3 square units.
Step-by-step explanation:
First, visualize the area. You can refer to the attachment below.
To find the area then, we will integrate y from x = 0 to x = 2. Therefore:
\(\displaystyle A=\int_0^2x^2\, dx\)
Integrate:
\(\displaystyle A=\frac{1}{3}x^3\Big|_{0}^2\)
Evaluate:
\(\displaystyle A=\frac{1}{3}[2^3-0^3]=\frac{1}{3}(8)=\frac{8}{3}\)
The area is 8/3 square units.

Answer:
A = \(\frac{8}{3}\) units²
Step-by-step explanation:

6. Simplify:
√900+ √0.09+√0.000009
Answers
The simplified value of the expression √900 + √0.09 + √0.000009 is 30.303.
To simplify the given expression, let's evaluate the square roots individually and then perform the addition.
√900 = 30, since the square root of 900 is 30.
√0.09 = 0.3, as the square root of 0.09 is 0.3.
√0.000009 = 0.003, since the square root of 0.000009 is 0.003.
Now, we can add these simplified values together
√900 + √0.09 + √0.000009 = 30 + 0.3 + 0.003 = 30.303
Therefore, the simplified value of the expression √900 + √0.09 + √0.000009 is 30.303.
for such more question on expression
https://brainly.com/question/4344214
#SPJ8
1
Drag the tiles to the correct boxes to complete the pairs.
Determine whether each pair of lines is perpendicular, parallel, or neither.
4y= 2x - 4
y = -2x +9
y = 2x + 4
2y = 4x - 7
Neither
2y = 4x + 4
y=-2x - 2
Perpendicular
Parallel
Answers
For lines to be parallel, the slope has to be the same.
For lines to be perpendicular, the slope has to be the negative reciprocal.
what are perpendicular lines?These lines always intersect at right angles.If two lines are perpendicular to the same line, they are parallel to each other and will never intersect. The sides of the right-angled triangle enclosing the right angle are perpendicular to each other.Two distinct lines intersecting each other at 90°, or a right angle, are called perpendicular lines.Learn more about perpendicular lines clcick here:
https://brainly.com/question/17565270
#SPJ13
imagine you are performing a two-way anova test, and you find a p-value for interaction of 0.07. what is the correct interpretation of this p-value with an alpha level of 0.05?
Answers
The correct interpretation of this p-value with an alpha level of 0.05 is explain below.
What is the correct interpretation of this p-value with an alpha level of 0.05?P-value is the margin of error importance inside a factual speculation test, addressing the likelihood of the event of a given occasion.
According to question:We have, P-value =0.07
Level of significance = 0.05
We know that,
P-value is less than level of significance, then H® is rejected,smaller the p-value longer the evidence that you should reject the null hypothesis.
Now P-value is greater than 0.05.
With a p-value greater than 0.05, fail to reject the H®.Look at multiple comparison of each Level of significance.
To know about P-value visit:
brainly.com/question/14790912
#SPJ4