jane had a collection of balloons she gave 1/4 of her collection to her sister. how many balloons does jane have now?
Answers
Answer:
3/4
Step-by-step explanation:
Explanation:
Becaus the fraction is 4/4 total, it means Jane had 4 balloons before. But because she gave 1/4 to her sister the equation is 4/4 - 1/4 = 3/4 .
Related Questions
Refer to ®F .
If DA = 7.4 centimeters, what is EF ?
Answers
If DA = 7.4 centimeters, then the radius of the circle EF is 3.7 inches.
What is meant by the radius of a circle?A radius of a circle or sphere is any of the line segments from its center to its perimeter in classical geometry, and in more modern usage, it is also their length. The name is derived from the Latin radius, which means both ray and spoke of a chariot wheel.
The radius of a circle is the distance between the circle's center and any point on its circumference. It is usually represented by the letters 'R' or 'r'. This number is significant in almost all circle-related formulas. A circle's area and circumference are also measured in terms of radius.
Here, DA is a diameter and EF is the radius.
Radius of a circle = 1/2 diameter
Where, d = 7.4
Radius of a circle, r = 1/2 d
Radius of a circle = 1/2(7.4)
Radius of a circle = 3.7
Therefore, the radius of the circle is 3.7 inches.
To learn more about the radius of the circle refer to:
brainly.com/question/26215003
#SPJ4
Diane sold some stuffs at a garage sale. She spent one-half of the money she made on a new bicycle. Next, she spent one-half of what was left on a portable stereo. If Diane had $40.00 left, how much money did she make from the garage sale
Answers
Answer:
$160
Step-by-step explanation:
Diane sold some stuffs at a garage sale.
Let the total value of the money Diane made = x
She spent one-half of the money she made on a new bicycle.
Amount spent on a Bicycle = 1/2 × x = 1/2x
Next,
Amount left
= x - 1/2x = 1/2x
She spent one-half of what was left on a portable stereo.
Amount spent spent on Portable stereo
= 1/2 × 1/2x
= 1/4x
If Diane had $40.00 left,
Hence:
The fraction of what was left is calculated as:
= x - (1/2x + 1/4x)
= x - (3/4x)
= 1/4x
Hence:
1/4x = $40
We can find the value of x now.
1/4 × x = $40
x/4 = $40
x = $40 × 4
x = $160
Therefore, the amount she made from the garage sale is $160
Answer:
Hey hey guys, it is 160.00
Step-by-step explanation:
pls need hlp in math<3

Answers
Answer:
45 g
Step-by-step explanation:
30/200 simplified = 3/20
3/20 as a decimal = 0.15
0.15 g of barley for 1 ml of milk
300 · 0.15 = 45
45 g of barley for 300 ml of milk
hope this helps :)
Factor the coefficient from 1.5a - 4.5
Answers
The answer is 1.5(a -3)
Find the value of the power
3⁴
Answers
Step-by-step explanation:
3⁴ can also be written as
3 × 3 × 3 × 3 = 81
hope this answer helps you dear!
Answer:
81
Step-by-step explanation:
3⁴
= 3 x 3 x 3 x 3
= 9 x 9
= 81
81 is the answer.
Will Mark brainlest help please please pease

Answers
Answer:
6
Step-by-step explanation:
very easy.
this simply means what is the value of x, so that the result of the function is 7.
remember, the domain is the interval of valid values for x.
and the range is the interval of valid values of y (or functional results).
so,
7 = (3x - 4)/2
14 = 3x - 4
18 = 3x
x = 6
so, for x = 6 the function delivers 7 as result.
if you can drive on 1/5 of a tank of gas in 3 hours how far can you drive on 1 tank of gas
Answers
Answer:
15 hours
Step-by-step explanation:
We know
You can drive on 1/5 of a tank of gas in 3 hours.
How far can you drive on 1 tank of gas?
We Take
3 x 5 = 15 hours
So, you can drive 15 hours on 1 tank of gas.
I am stuck on how I got 25 for an answer (2+3)^2
Answers
Answer:
25
Step-by-step explanation:
(2+3)=5
5^2=25
I got 25 too-
(2+3)^2
First I added 2+3 which is 5
Then square that answer.. 5^2= 25
arts academy requires there to be 6 teachers for every 144 students and 3 tutors for every 24 students. How many students does the academy have per teacher? Per tutor? How many tutors does the academy need if it has 64 students?
Answers
Answer:
the teachers would have 24 students per teacher. 10 students per tutor. There would need to be 11 tutors
Step-by-step explanation:
each tutor would have 10 students then if you do 11 times 10 you get 11
(hope this helps can I pls have brainlist (crown)☺️)
Point M is the midpoint of line segment CD,
shown below.
What are the coordinates of point M?
C (6,10)
M
D (20, 18)
Answers
Answer:
M(13, 14)-------------------------
Each coordinate of the midpoint is the average of endpoints:
x = (6 + 20)/2 = 26/2 = 13y = (10 + 18)/2 = 28/2 = 14Therefore M is (13, 14).
Omani drives 66 miles in 1.5 hours
Adedi drives 56 km in 1 hour 15 min
Workout the difference between their average speeds km/h
1 mile = 1.6 km
Answers
Answer:
25.6 km/h
Step-by-step explanation:
Omani:
First, 1.5 hours = 1 hour and 30 minutes
and 66 miles = 105.6 km (66 x 1.6 = 105.6)
105.6 / 1.5 = 70.4 km/h
Omani's speed is 70.4 km/h
Adedi:
1 hour and 15 minutes is 1.25 hours
she drives 56 km in 1.25 hours
So 56 / 1.25 = 44.8 km/h
Adedi's speed is 44.8 km/h
Difference:
70.4 - 44.8 = 25.6 km/h
Omani is faster than Adedi with 25.6 km/h
Problem 6 (16 points). An individual opens a savings account with an initial investment of $500. The bank offers her an annual interest rate of 9%, which is continuously computed. She decides to deposit $200 every month. a) Write an initial value problem that models this investment over time. b) Solve the IVP.
c) What is the value of the investment in 2 years? d) After the 2 year mark, she increases her monthly investment to $300. What is the value of the investment a year later? Show all your work for full credit; you may use a calculator for this problem. Problem 7 (16 points). Solve the following IVP: ycosx−2xe y coz x − 2x eʸ -6x² - (x² eʸ - sin x - 4) yᶦ = 0; y (π) = 0
Answers
The investment problem is modeled by an initial value problem (IVP) where the rate of change of the investment is determined by the initial investment, monthly deposits, and the interest rate.
a) The investment problem can be modeled by an initial value problem where the rate of change of the investment, y(t), is given by the initial investment, monthly deposits, and the interest rate. The IVP can be written as:
dy/dt = 0.09y + 200, y(0) = 500.
b) To solve the IVP, we can use an integrating factor to rewrite the equation in the form dy/dt + P(t)y = Q(t), where P(t) = 0.09 and Q(t) = 200. Solving this linear first-order differential equation, we obtain the solution for y(t).
c) To find the value of the investment after 2 years, we substitute t = 2 into the obtained solution for y(t) and calculate the corresponding value.
d) After 2 years, the monthly deposit increases to $300. To find the value of the investment a year later, we substitute t = 3 into the solution and calculate the value accordingly.
Learn more about Initial Value Problem: brainly.com/question/31041139
#SPJ11
Angles 1 and 2 are supplementary. 2 lines intersect to form angles 1 and 2. which equation represents the relationship between their measures? mangle1 mangle2 = 90° mangle1 mangle2 = 100° mangle1 mangle2 = 180° mangle1 mangle2 = 200°
Answers
Answer:
angle 1+angle 2 = 180 degrees
Step-by-step explanation:
when 2 angles are supplementary, they equal 180 degrees when they are added up. Because angles 1 and 2 are supplementary, this means that angle 1 + angle 2 equals 180 degrees.
Answer:
mAngle1 + mAngle2 = 180°
Step-by-step explanation:
edge 2022
75
Which degree measurement is equivalent to radians?
6
A. 1050
B. 210°
C. 240°
D. 420°

Answers
Answer:
B. 210°
hope it helps
have a nice day
A business has found that it can sell 750 items if it sets its price to $63.92. However, if it lowers its price to $43.18, it can sell 870 items. (a) Find the linear demand equation (price function) for selling x items. (ound to 4 dechmorpaces) p(x)= It costs the business $10.94 per item to produce and they have $3,150 in overhead each month. (b) Find the linear Cost, and quadratic Revenue and Profit functions for producing/selling x items: pound to a deocina phasen C(x)= R(x)=P(x)= x+x2+x2+x+x+ (c) How many items should the company sell to break even? What price should they set to do So? (lower quantity) They could sell items at a price of $ each R (higher quantity) They could sell items at a price of $ e
Answers
The company must sell either 247.74 (higher quantity) or 116.32 (lower quantity) items to break even. The corresponding price to do so is $43.18 (for 247.74 items) and $63.92 (for 116.32 items).
Let p = price and x = number of items sold
We know that when the price is $63.92, the company can sell 750 items. Thus we have the equation:
p = 63.92 and x = 750 items
We also know that when the price is $43.18, the company can sell 870 items. Thus we have the equation:
p = 43.18 and x = 870 items
From the two equations above, we can calculate the linear demand equation by using the slope-intercept form, y = mx + b, as follows:
p = (43.18 - 63.92)/(870 - 750)x + 63.92
p = -20.74/120x + 63.92
p = -0.172x + 63.92.
Therefore, the linear demand equation (price function) for selling x items is p(x) = -0.172x + 63.92 (b) To find the linear Cost and quadratic Revenue and Profit functions:
We know that it costs the business $10.94 per item to produce and they have $3,150 in overhead each month.
Thus, the linear cost function for producing x items is:
C(x) = 10.94x + 3150
The quadratic revenue function for selling x items is:
R(x) = -0.1722x² + 63.92x
The profit function for producing and selling x items is:
P(x) = -0.1722x² + 63.92x - 10.94x - 3150
P(x) = -0.1724x² + 53.98x - 3150 (c) To break even, the company must make zero profit, thus P(x) = 0. Solving for x, we have:
0 = -0.1724x² + 53.98x - 3150
0.1724x² - 53.98x + 3150 = 0
Using the quadratic formula:
x = (53.98 ± √[53.982 - (4)(0.1724)(3150)])/(2(0.1724))
x = 182.08 ± 65.66
Therefore, the company must sell either 247.74 (higher quantity) or 116.32 (lower quantity) items to break even. The corresponding price to do so is $43.18 (for 247.74 items) and $63.92 (for 116.32 items).
Learn more about the quadratic Revenue here:
https://brainly.com/question/28989698.
#SPJ4
Find the determinant associated with each matrix below. Is the matrix nonsingular and does its inverse exist? a) A=[
2
0
0
2
] b) B=[
1
4
2
8
] c) C=[
6
−15
−2
5
] d) D=[
0
3
2
2
]
Answers
a) Matrix A: Determinant = 4, nonsingular, inverse exists.
b) Matrix B: Determinant = 0, singular, inverse does not exist.
c) Matrix C: Determinant = 0, singular, inverse does not exist.
d) Matrix D: Determinant = -6, nonsingular, inverse exists.
To find the determinant of a matrix, we can use the formula for a 2x2 matrix:
For a matrix A = [a b; c d], the determinant det(A) is calculated as: det(A) = ad - bc.
Let's calculate the determinants for each matrix:
a) A = [2, 0; 0, 2]
det(A) = (2 * 2) - (0 * 0) = 4 - 0 = 4
b) B = [1, 4; 2, 8]
det(B) = (1 * 8) - (4 * 2) = 8 - 8 = 0
c) C = [6, -15; -2, 5]
det(C) = (6 * 5) - (-15 * -2) = 30 - 30 = 0
d) D = [0, 3; 2, 2]
det(D) = (0 * 2) - (3 * 2) = 0 - 6 = -6
Now, let's determine if each matrix is nonsingular and if its inverse exists:
A matrix is nonsingular if and only if its determinant is non-zero.
a) Matrix A: det(A) = 4 ≠ 0
Since the determinant is non-zero, matrix A is nonsingular and its inverse exists.
b) Matrix B: det(B) = 0
The determinant is zero, which means matrix B is singular, and its inverse does not exist.
c) Matrix C: det(C) = 0
The determinant is zero, which means matrix C is singular, and its inverse does not exist.
d) Matrix D: det(D) = -6 ≠ 0
Since the determinant is non-zero, matrix D is nonsingular and its inverse exists.
To summarize:
a) Matrix A: Determinant = 4, nonsingular, inverse exists.
b) Matrix B: Determinant = 0, singular, inverse does not exist.
c) Matrix C: Determinant = 0, singular, inverse does not exist.
d) Matrix D: Determinant = -6, nonsingular, inverse exists.
Learn more about matrix here:
https://brainly.com/question/28180105
#SPJ11
Consider the points below. P(θ),−4,0),Q(5,1,−2),R(6,4,1) (a) Find a nonzero vector orthogonal to the plane through the points P,Q, and R. (b) Find the area of the triangle PQR.
Answers
(a) A nonzero vector orthogonal to the plane through the points P, Q, and R is (9, -17, 35). (b) The area of triangle PQR is \(\sqrt\)(811) / 2.
(a) To determine a nonzero vector orthogonal to the plane through the points P, Q, and R, we can first find two vectors in the plane and then take their cross product. Taking vectors PQ and PR, we have:
PQ = Q - P = (5, 1, -2) - (-4, 0, 0) = (9, 1, -2)
PR = R - P = (6, 4, 1) - (-4, 0, 0) = (10, 4, 1)
Taking the cross product of PQ and PR, we have:
n = PQ x PR = (9, 1, -2) x (10, 4, 1)
Evaluating the cross product gives n = (9, -17, 35). Therefore, (9, -17, 35) is a nonzero vector orthogonal to the plane through points P, Q, and R.
(b) To determine the area of triangle PQR, we can use the magnitude of the cross product of vectors PQ and PR divided by 2. The magnitude of the cross product is given by:
|n| = \(\sqrt\)((9)^2 + (-17)^2 + (35)^2)
Evaluating the magnitude gives |n| = \(\sqrt\)(811).
The area of triangle PQR is then:
Area = |n| / 2 = \(\sqrt\)(811) / 2.
To know more about nonzero vector refer here:
https://brainly.com/question/32673773#
#SPJ11
Which of the following are solutions to the equation below?
Check all that apply.
X2 + 10x+ 25 = 8
Answers
X^2+10x+25 =8
Answer shown in figures below
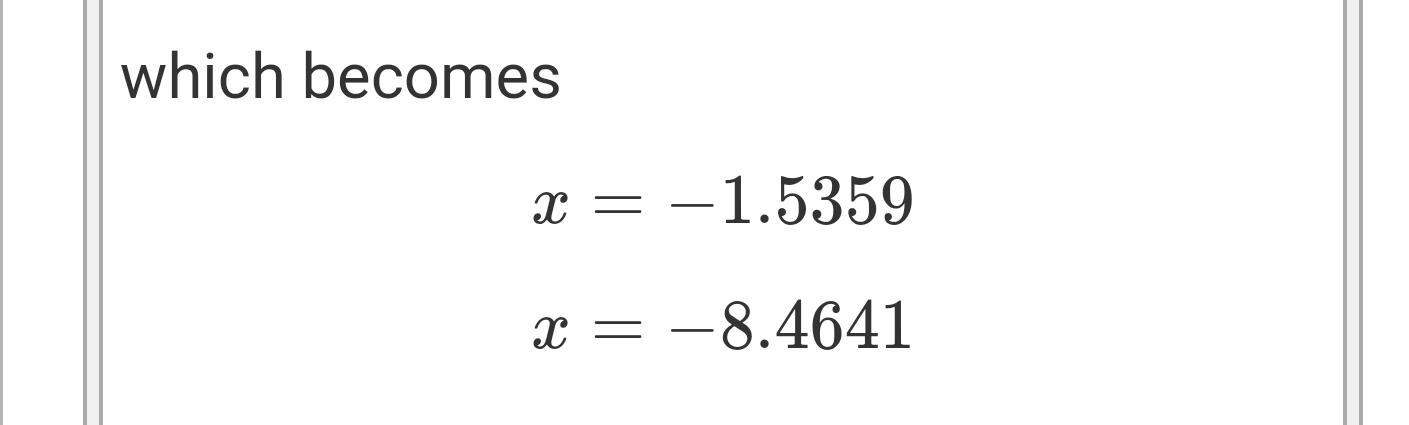

Find the Cartesian inequation for the region represented by |z+6|≤|z-51 Please simplify your answer. Note. The inequality sign ≤ is entered as the pair of consecutive symbols: <= Also note that Maple rewrites inequalities that have been entered using >= (i.e. ≥) in terms of ≤ (and sometimes it does this in a quite inelegant way!) Answer:
Answers
The given Cartesian inequality, let's break it down into two separate cases:
Case 1: When z is a real number
In this case, we can rewrite the inequality as:
|z + 6| <= |z - 51|
This can be further simplified using the definition of absolute value:
(z + 6) <= (z - 51) OR -(z + 6) <= (z - 51)
Simplifying the two inequalities separately:
(z + 6) <= (z - 51)
z + 6 <= z - 51
6 <= -51 (contradiction)
This inequality has no solutions since 6 is not less than or equal to -51.
-(z + 6) <= (z - 51)
-z - 6 <= z - 51
-2z <= -45
2z >= 45
z >= 22.5
Therefore, for real numbers z, the solution is z >= 22.5.
Case 2: When z is a complex number
In this case, we can rewrite the inequality using the modulus properties:
|z + 6|^2 <= |z - 51|^2
Expanding both sides of the inequality:
(z + 6)(z + 6)^* <= (z - 51)(z - 51)^*
Where (z + 6)^* and (z - 51)^* denote the complex conjugates of (z + 6) and (z - 51), respectively.
Simplifying the inequality:
(z + 6)(z + 6)^* <= (z - 51)(z - 51)^*
Let's denote z = x + yi, where x and y are real numbers.
Expanding both sides:
(x + 6 + yi)(x + 6 - yi) <= (x - 51 + yi)(x - 51 - yi)
(x^2 + 12x + 36 + y^2) <= (x^2 - 102x + 2601 + y^2)
12x + 36 <= -102x + 2601
114x <= 2565
x <= 22.5
Therefore, for complex numbers z, the solution is x <= 22.5.
Combining the results from both cases, we have:
z >= 22.5 or x <= 22.5 (where z is a complex number and x is its real part)
Thus, the Cartesian inequality for the given region is:
z >= 22.5 or Re(z) <= 22.5
learn more about numbers click here;
https://brainly.com/question/3589540
#SPJ11
what is the GCF of 12x^2 and 18x
Answers
Answer: 6x
Step-by-step explanation:
Factor each term and see what they have in common.
12x²: 2 · 2 · 3 · x · x
18x: 2 · 3 · 3 · x
The common factors are: 2 · 3 · x = 6x
x = -6 + y
X - 3y = 28

Answers
x= -23
hope this helps!!
What is the value of y in the solution of the system of equations? 10x+24 y=9 8 x+60 y=14.
Answers
The solution to the equation is y = 1/6
Given data:
To find the value of y in the solution of the system of equations:
10x + 24y = 9 ...(1)
8x + 60y = 14 ...(2)
We can use the method of substitution or elimination to solve the system. Let's use the method of substitution:
From equation (1), isolate x:
10x = 9 - 24y
x = (9 - 24y)/10
Now substitute this value of x into equation (2):
8((9 - 24y)/10) + 60y = 14
Simplify and solve for y:
(72 - 192y)/10 + 60y = 14
72 - 192y + 600y = 140
408y = 68
y = 68/408
y = 1/6
Hence, the value of y in the solution of the system of equations is y = 1/6.
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ4
V3 and but outside r, r2 = 2 sin (20) then set up integral(s) for area of the following: (12 pts) Sketch the graph of 1 a) Inside r. b) Inside r, but outside r; c) Inside both ri and r
Answers
To find the areas of the given regions, we need to set up integrals. The regions are described.
a) To find the area inside r, we need to set up the integral based on the given equation r1 = 2 sin(20). We can sketch the graph of r1 as a circle with radius 2 sin(20) centered at the origin. The integral for the area can be set up as ∫∫ \(r1^2\) dA, where dA represents the area element.
b) To find the area inside r2 but outside r1, we need to set up the integral based on the given equation r2 = 3. We can sketch the graph of r2 as a circle with radius 3 centered at the origin. The region between r1 and r2 can be visualized as the area between the two circles. The integral for the area can be set up as ∫∫ (\(r2^2\) - \(r1^2\)) dA.
c) To find the area inside both r1 and r2, we need to find the overlapping region between the two circles. This can be visualized as the region common to both circles. The integral for the area can be set up as ∫∫ \(r1^2\)dA, considering the area within the smaller circle.
These integrals can be evaluated to find the actual area values for each region.
Learn more about graph here:
https://brainly.com/question/17267403
#SPJ11
sarah has plantains and pomegranates in a ratio of 18/176 how many ponogranates does she have if she had 9 plantains
Answers
Answer:
88
Step-by-step explanation:
18/2=9
176/2=88
Hope this helps! :)
how many frequent flyer program members are reported in newspaper quintile v? remember to report your answer with regards to the (000) format!
Answers
The number of frequent flyer program members in newspaper quintile V.
The information related to that specific quintile.
Unfortunately, you didn't provide the required data to calculate the number of frequent flyer program members in newspaper quintile V.
To understand what the given data represents.
Since the question is asking for the number of frequent flyer program members in newspaper quintile V.
The data is provided, I will guide you through a step-by-step process to find the answer and ensure that it is reported in the (000) format, as you requested.
Please provide the relevant data, and I'll be more than happy to help you calculate the answer.
Once the information is given, I will walk you through a step-by-step procedure to identify the solution and make sure it is presented in the (000) format, as you asked, when I have the data.
Comprehend what the provided data means.
Given that the number of frequent flyers programmed members in newspaper quintile V is the subject of the issue.
Information pertinent to that particular percentile.
Unfortunately, you didn't supply the information needed to determine how many people in newspaper quintile V are members of frequent flyer programmed.
The pertinent information, and I'll be pleased to assist you in coming up with the solution.
For similar questions on Members
https://brainly.com/question/868250
#SPJ11
Cones A and B both have volume 48bold pi cubic units, but have different dimensions. Cone A has radius 6 units and height 4 units. Find one possible radius and height for Cone B. Explain how you know Cone B has the same volume as Cone A.
Answers
Cone B could have a radius of 4 units and a height of 3 units
We know that the volume of Cone A is given by:
V(A) = \((\frac{1}{3})\pi r^2h\) = \((\frac{1}{3} )\pi (6^2)(4)\) = 48π
To find one possible set of dimensions for Cone B, we can use the fact that the volume of Cone B is also 48π. Let's choose a different radius and height for Cone B and see if it satisfies the volume requirement:
V(B) = \((\frac{1}{3})\pi r^2h\) = \((\frac{1}{3})\pi (r^2)(3h)\)
Since V(A) = V(B), we have:
\((1/3)\pi (6^2)(4)\) = \((1/3)\pi (r^2)(3h)\)
Simplifying this equation, we get:
\(r^2h\) = 48
We can choose any value of r and h that satisfy this equation. For example, let's choose r = 4 and h = 3:
\(r^2h\) = \(4^2(3)\) = 48
So, Cone B could have a radius of 4 units and a height of 3 units, and its volume would be 48π cubic units.
We know that Cone B has the same volume as Cone A because they both have a volume of 48π cubic units. This means that if we were to fill Cone A with water and pour it into Cone B, the water level in Cone B would rise to the same height as in Cone A. Therefore, both cones would have the same amount of water and hence the same volume.
To learn more about radius, refer:-
https://brainly.com/question/15005181
#SPJ1
Mr. Yukilous has hired some workers to install a patio. The patio will be a square, 5 feet on edge. The workers charge $30 per square foot for the patio tiles, plus $600 for the labor. Write an expression giving the total cost, then simplify it to find that cost. To answer this question, please select the correct multiple choice response below.
Answers
Answer:
Step-by-step explanation:
reeeeeeeeee
Vera hiked a total of 138 miles in 12 days. She hiked the same distance each day. Write and solve a multiplication equation to find the number of miles m she hiked each day.
Answers
Answer:
11 miles ah day
Step-by-step explanation:
11.5 x 12
Answer:
138 divided by 12 =11.5
Step-by-step explanation:
or you can do 11.5 x 12 to check your answer
50 Points pls help!
Question: Fred drew the footprint of a stage he was planning to build for his band on a coordinate plane. He decided he wanted to make it smaller because he wanted to make sure it fit at every venue.
Please help me solve letter A and B :)

Answers
Answer:
A) Picture added,B) 26 units.=========================
Part AThe smaller figure is added, considering the coordinates of the image follow the rule:
(x, y) → (0.5x, 0.5y)Smaller stage is in blue. See attached
Part BSince each side is half the original, the perimeter of the image is half the larger one:
P = 52/2 = 26 units
given the equation 2x - y = 12, which equation is written in slope intercept form?
Answers
When we express the equation 2x - y = 12 in slope intercept form, the result obtained is y = 2x - 12 (2nd option)
How do i obtain the slope intercept form for equation?The slope intercept form for an equation is written as illustrated below:
y = mx + c
Where
y and x are the y and x coordinatec is the intercept on the x axisWith the above information, we can obtain the slope intercept form of the equation. Details below:
Equation in point slope: 2x - y = 12Slope intercept form =?2x - y = 12
Rearrange to make y the subject of the expression, we have
2x = 12 + y
y = 2x - 12
Thus, we can conclude that the equation in the slope intercept form is
y = 2x - 12 (2nd option)
Learn more about coordinate geometry:
https://brainly.com/question/21298390
#SPJ4
Complete question:
Given the equation 2x - y = 12, which equation is written in slope intercept form?
y = -2x + 12
y = 2x - 12
y = 2x + 12
y = -2x - 12