Jamie needs to build a fence around his garden, as illustrated by polygon ABCDEF on the coordinate grid below. If each unit represents one yard, what is the total length of Jamie's fence in yards?
(72 POINTS)
Please don't just answer for points if you know the answer you know the answer
(Homework assignment worth a test grade so need someone who knows their stuff)


Answers
Answer:
C. 26 yards
Step-by-step explanation:
Jamie's fence total length = perimeter of the polygon
Perimeter of the polygon = AB + BC + CD + DE + EF + FA
AB, FA and DE can be worked accordingly as shown below:
AB = |-5 - 0| = 5 units
FA = |5 - 2| = 3 units
DE = |1 -(-2)| = 3 units
BC, CD, and EF can be calculated using the formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Distance between B(0, 5) and C(4, 2):
\( BC = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Let,
\( B(0, 5) = (x_1, y_1) \)
\( C(4, 2) = (x_2, y_2) \)
\( BC = \sqrt{(4 - 0)^2 + (2 - 5)^2} \)
\( BC = \sqrt{(4)^2 + (-3)^2} \)
\( BC = \sqrt{16 + 9} = \sqrt{25} \)
\( BC = 5 units \)
Distance between C(4, 2) and D(1, -2)
\( CD = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Let,
\( C(4, 2) = (x_1, y_1) \)
\( D(1, -2) = (x_2, y_2) \)
\( CD = \sqrt{(1 - 4)^2 + (-2 - 2)^2} \)
\( CD = \sqrt{(-3)^2 + (-4)^2} \)
\( CD = \sqrt{9 + 16} = \sqrt{25} \)
\( CD = 5 units \)
Distance between E(-2, -2) and F(-5, 2):
\( EF = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Let,
\( E(-2, -2) = (x_1, y_1) \)
\( F(-5, 2) = (x_2, y_2) \)
\( EF = \sqrt{(-5 -(-2))^2 + (2 -(-2))^2} \)
\( EF = \sqrt{(-3)^2 + (4)^2} \)
\( EF = \sqrt{9 + 16} = \sqrt{25} \)
\( EF = 5 units \)
Total length of the wall in yards = 5 + 5 + 5 + 3 + 5 + 3 = 26 yards
Related Questions
Can someone pls help me with this question

Answers
Answer: its correct
Step-by-step explanation: 4 is the answer
Answer:
ur good, pretty sure its 4 :)
The functions f(x), g(x), and h(x) are shown below. Select the option that represents the ordering of the functions according to their average rates of change on the interval 3≤x≤4 goes from least to greatest.


Answers
Solution:
The rate of change, m, of a function f is;
\(m=\frac{f(b)-f(a)}{b-a}\)Given the graph, f(x);
Its rate of change over the given interval is;
\(\begin{gathered} m=\frac{f(4)-f(3)}{4-3} \\ \\ m=\frac{6-(-2)}{1} \\ \\ m=8 \end{gathered}\)Given the table of g(x);
Its rate of change over the interval is;
\(\begin{gathered} m=\frac{g(4)-g(3)}{4-3} \\ \\ m=\frac{13-18}{1} \\ \\ m=-5 \end{gathered}\)Also, given the function of h(x);
\(\begin{gathered} h(x)=-x^2+3x+21 \\ \\ h(4)=-(4)^2+3(4)+21 \\ \\ h(4)=-16+12+21 \\ \\ h(4)=17 \\ \\ h(3)=-(3)^2+3(3)+21 \\ \\ h(3)=-9+9+21 \\ \\ h(3)=21 \end{gathered}\)Its rate of change over the interval is;
\(\begin{gathered} m=\frac{17-21}{4-3} \\ \\ m=-\frac{4}{1} \\ \\ m=-4 \end{gathered}\)The order of the rate of change from the least to the greatest is;
\(-5,-4,8\)CORRECT OPTION:
\(g(x),h(x),f(x)\)

3x^3-2x^2+7x+9 divided by x^2-3x
Answers
The quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
What is Division?A division is a process of splitting a specific amount into equal parts.
We have to find 3x³-2x²+7x+9 divided by x²-3x
3x³-2x²+7x+9 is the dividend and x²-3x is the divisor.
The steps to solve this are given below.
Step 1: Take the first digit of the dividend from the left. Check if this digit is greater than or equal to the divisor.
Step 2: Then divide it by the divisor and write the answer on top as the quotient.
Step 3: Subtract the result from the digit and write the difference below.
Step 4: Bring down the next digit of the dividend (if present).
Step 5: Repeat the same process.
Hence, the quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ9

If a random sample of 47 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 0.2 millimeters?
Answers
Complete Question
Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 143 millimetres, and a standard deviation of 5. If a random sample of 47 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 0.2 millimetres? Round your answer to four decimal places.
Answer:
The probability is \(P(|\= x - \mu | \ge 0.2 ) = 0.78394\)
Step-by-step explanation:
From the question we are told that
The sample size is n = 47
The mean diameter is \(\mu = 143\)
The standard deviation is \(\sigma = 5\)
Generally the standard error of the mean is mathematically represented as
\(\sigma_{x} = \frac{\sigma }{\sqrt{n} }\)
=> \(\sigma_{x} = \frac{5 }{\sqrt{47} }\)
=> \(\sigma_{x} = 0.7293\)
Generally the probability that the sample mean will differ from the population mean by more than 0.2 milli meters is mathematically represented as
\(P(|\= x - \mu | \ge 0.2 ) = P(\frac{|\= x - \mu|}{\sigma_{x}} \ge \frac{0.2}{0.7293} )\)
\(\frac{|\= x - \mu | -\mu}{\sigma } = |Z| (The \ standardized \ value\ of \ {|\= x - \mu | )\)
=> \(P(|\= x - \mu | \ge 0.2 ) = P(|Z| \ge 0.2742 )\)
=> \(P(|\= x - \mu | \ge 0.2 ) = P(Z < - 2742) + P(Z > 0.2742)\)
From the z table the area under the normal curve to the left corresponding to -2.742 is
\(P(Z < -0.2742) =0.39197\)
From the z table the area under the normal curve to the right corresponding to 2.742 is
P(Z > 0.2742) = 0.39197
So
\(P(|\= x - \mu | \ge 0.2 ) = 0.39197 + 0.39197\)
\(P(|\= x - \mu | \ge 0.2 ) = 0.78394\)
Use the diagram below. What is the value of z?
(Picture included) it would mean sm if anyone could help

Answers
\(z = 29°\)
Step-by-step explanation:
According to the triangle angle sum theorem, the sum of the interior angles of a triangle is 180°. So for \(\triangle{ABD},\) the sum of its interior angles is
\(43 + 59 + x = 180\)
\(\Rightarrow x = 78°\)
But \(\angle{x}\) is supplementary with \(\angle{y}\) so that
\(x + y = 180 \Rightarrow y = 180 - 78 = 102°\)
Now that we know the value of y, we apply the triangle angle sum theorem to \(\triangle{BDC}\) and we get
\(49 + y + z = 180 \Rightarrow 49 + 102 + z = 180\)
Solving for z, we finally get
\(z = 29°\)
Suppose IQ scores were obtained for 20 randomly selected sets of couples. The 20 pairs of measurements yield x=97.47​, y=97.35​, r=0.892​, ​P=0.000, and y=-9.15+1.09x​, where x represents the IQ score of the wife. Find the best predicted value of y given that the wife has an IQ of 104​? Use a significance level of 0.05.
Answers
Question:
Suppose IQ scores were obtained for 20 randomly selected sets of couples. The 20 pairs of measurements yield x' =97.47, y' =97.35, r=0.892, P=0.000, and y^=-9.15+1.09x, where x represents the IQ score of the wife. Find the best predicted value of y given that the wife has an IQ of 104? Use a significance level of 0.05.
Answer:
y^ = 104.21
Step-by-step explanation:
Given:
n = 20
x' = 97.47
y' = 97.35
r = 0.892
P-value = 0.000
y^ = -9.15 + 1.09x
Here, the wife has an IQ of 104.
The regression equation here is given as:
y^ = -9.15 + 1.09x
Let x represent the IQ of the wife.
x = 104
Hence, the best predicted value of y^ will be:
Let's substitute 104 for x in tge regression equation.
y^ = -9.15 + 1.09(104)
y^ = - 9.15 + 113.36
y^ = 104.21
Therefore, the best predicted value of y^ = 104.21
it is two plus two what does it equal?
Answers
Shen bought a desk on sale for $218.40. This price was 72% less than the original price. What was the original price?
Answers
Answer:
780
Step-by-step explanation:
In this example we will call Original Price = y
72%=0.72
218.40=0.72*y
1-0.72=0.28
218.4÷0.28=780
Math algebra 2 help please.

Answers
Answer:
steps below
Step-by-step explanation:
5. x³-8x²-4x+32 = x²(x-2) -6x(x-2) -16(x-2) = (x-2)(x²-6x-16)= (x-2)(x+2)(x-8)
6. 27x³+125 = (3x)³ + 5³ = (3x+5)(9x²-15x+25)
please look at the picture below
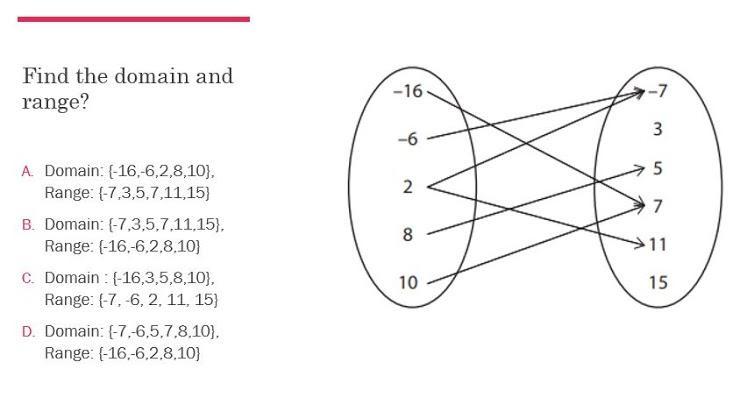
Answers
Answer:
A
Step-by-step explanation:
domain is the input and range is the output
4.1 Unit Rates
Find each unit rate. Round to the nearest hundredth, if nece
1. $140 for 18 ft?
Answers
Answer: 17.5
Step-by-step explanation:
Each grid square is 1 square unit. Find the area, in square units, of the shaded region without counting every square. Be prepared to explain your reasoning.

Answers
Answer:
The area of the shaded region is 27 units^2.
Step-by-step explanation:
Area of outer square = 6^2 = 36 units^2
Area of inner square = 3^2 = 9 units^2
Area of shaded region
= 36 units^2 - 9 units^2 = 27 units^2
The area of a shaded region in a unit grid can be found either by subtracting the area of unshaded regions from the total grid area or by adding up the areas of identifiable shapes within the shaded region.
Explanation:To find the area of the shaded region without counting every square, you can use a few different strategies, such as identifying and subtracting the area of unshaded regions from the total grid area, or recognizing and adding together larger, easily countable shapes within the shaded region.
For example, if your grid is 10x10 units, the total area would be 100 square units. If, within that grid, there are 20 unshaded squares, you can subtract this from the total area to find the area of the shaded region. So, 100 total square units - 20 unshaded square units = 80 shaded square units. This approach works best when the number of unshaded squares is relatively small or easily countable.
Alternatively, if the shaded region forms easily identifiable shapes (like a 5x5 square or a 3x10 rectangle), you can add the areas of these shapes together to get the total shaded area. This approach works best when the shaded region forms a few large, simple shapes.
Learn more about Area of Shaded Region here:https://brainly.com/question/20162990
#SPJ2
A manufacturing process makes rods that vary slightly in length but follow a normal distribution with mean length 25 cm and standard deviation 2.60. What is the probability of randomly selecting a rod that is shorter than 22 cm
Answers
Answer:
The probability of randomly selecting a rod that is shorter than 22 cm
P(X<22) = 0.1251
Step-by-step explanation:
Step(i):-
Given mean of the Population = 25cm
Given standard deviation of the Population = 2.60
Let 'x' be the random variable in normal distribution
Given x=22
\(Z = \frac{x-mean }{S.D} = \frac{22-25}{2.60} = -1.15\)
Step(ii):-
The probability of randomly selecting a rod that is shorter than 22 cm
P(X<22) = P( Z<-1.15)
= 1-P(Z>1.15)
= 1-( 0.5+A(1.15)
= 0.5 - A(1.15)
= 0.5 - 0.3749
= 0.1251
The probability of randomly selecting a rod that is shorter than 22 cm
P(X<22) = 0.1251
Find the average rate of change

Answers
Answer:
(a) The average rate of change from 0 to 2 is 6
(b) The average rate of change from 3 to 5 is 24
(c) The average rate of change from -3 to 0 is -9
Step-by-step explanation:
The formula for the average rate of change (AROC) is given by:
\(AROC=\frac{f(b)-f(a)}{b-a}\)
(a):
Finding the AROC from 0 to 2
To find the average rate of change from 0 to 2, we use f(2) and f(0), while we plug in 2 for b and 0 for a:
\(\frac{f(2)-f(0)}{(2-0)}\\ \\\frac{((3(2)^2+4)-(3(0)^2+4))}{(2-0)} \\\\\frac{(16-4)}{(2)}\\ \\\frac{12}{2}\\ \\6\)
Thus, the average rate of change from 0 to 2 is 6.
(b):
Finding the AROC from 3 to 5:
To find the average rate of change from 3 to 5, we use f(5) and f(3), while we plug in 5 for b and 3 for a:
\(\frac{f(5)-f(3)}{(5-3)}\\ \\\frac{((3(5)^2+4)-(3(3)^2+4))}{(2-0)} \\\\\frac{(79-31)}{(2)}\\ \\\frac{48}{2}\\ \\24\)
Thus, the average rate of change from 5 to 3 is 24.
(c):
To find the average rate of change from -3 to 0, we use f(0) and f(-3), while we plug in 0 for b and -3 for a:
\(\frac{f(0)-f(-3)}{(0-(-3))}\\ \\\frac{((3(0)^2+4)-(3(-3)^2+4))}{(0+3)} \\\\\frac{(4-31)}{(3)}\\ \\\frac{-27}{3}\\ \\-9\)
Thus, the average rate of change from -3 to 0 is -9.
29.For n ≥ 3, a pattern can be made by overlapping n circles, each of circumference 1 unit, so that each circle passes through a central point and the resulting pattern has order-n rotational symmetry.
For instance, the diagram shows the pattern where n = 7.
If the total length of visible ares is 60 units, what is n?

Answers
The value of n can be determined by finding the number of visible arcs in the pattern, which is 30 in this case.
To determine the value of n, we need to find the relationship between the total length of visible areas and the number of circles (n).
In the given pattern, each circle contributes to the visible area twice: once as its circumference and once as the overlapping part with the adjacent circles. Since the circumference of each circle is 1 unit, the visible area contributed by each circle is 2 units.
Therefore, the total length of visible areas can be expressed as 2n. Given that the total length is 60 units, we can set up the equation:
2n = 60
Solving this equation, we find:
n = 60/2 = 30
Thus, the value of n is 30.
For more questions on number of visible arcs:
https://brainly.com/question/31336038
#SPJ8
Identify the kind of sample that is described.
A football coach randomly selected the varsity or junior varsity team and then asks all players from that team their opinion on a new logo.
A. Stratified
B. Simple Random
C. Voluntary Response
D. Cluster
E. Systematic
Answers
The given sample of the randomly selected players from the teams as described is a stratified sample. Hence, the right answer is option A.
In a stratified sample, the population is divided into groups (or strata) based on some characteristic, and a random sample is selected from each group. In this case, the population is the football players, and the groups are the varsity and junior varsity teams. The coach randomly selects one of these teams and then asks all players from that team their opinion on a new logo.
This type of sampling is used when the population is divided into subgroups that are different in some way, and the researcher wants to ensure that these subgroups are represented in the sample. In this case, the coach wants to ensure that both varsity and junior varsity players are represented in the sample, as they may have different opinions on the new logo.
It's not a simple random sample because he selected the team first and then the players. Also, it's not a voluntary response sample because the coach is selecting the players.
It's not a cluster sample because the coach is not selecting the players based on location or geographic proximity, and it's not a systematic sample because he is not selecting the players based on the order in which they appear in a list or a database.
Read more about samples and their kinds:
brainly.com/question/29721721
#SPJ4
If a plate is moving 3.3 cm/yr, what distance [in kilometers (km)] will the plate move in 1 million years?
Answers
\(\huge{\textbf{\textsf{{\color{pink}{An}}{\red{sw}}{\orange{er}} {\color{yellow}{:}}}}}\)
33 km3.3cm = 0.000033km (divide by 100,000.
So, 0.000033km/yr.
0.000033 × 1,000,000
=33km
Thanks Hope it helpsThe number of votes received by Margie and Rachel are listed below. How many
TOTAL votes were cast in the election?
Answers
We have that Total votes cast in the election is the vote cast for Margie and Rachel summed up
\(Total\ vote=\sum Rachel +\sum Margie\)
It is important to note that an election comprise of two or more candidates facing off against each other to decide who a group of people want for a position
From the Question we are told that
There is suppose to be a table of votes cast
Generally the Total votes cast in the election is the vote cast for Margie and Rachel summed up
Therefore
\(Total\ vote=\sum Rachel +\sum Margie\)
For more information on this visit
https://brainly.com/question/24541453
what is the square root of 481
Answers
Answer:
21.9317122
Step-by-step explanation:
Answer:
21.9317121995
Step-by-step explanation:
PLZ HELP ITS DUE TODAY!!!!
Show work!!!

Answers
Answer: -7/20
Explanation; look at the imagine attached

Mark has a container in the shape of a cube. He
uses 64 cubes with Side lengths of linch to completely
fill the container. What is the edge length of the
Container?
Answers
Answer:
x * x = 64
x = 8 or 4 inches is the edge length of the container.
Answer:
4 inches is the edge lenght of the container
Choose the graph of the equation 4x + 3y = –24.
Answers
Answer:
the slope intercept form of the equation is y= - \(\frac{4}{3}\)x -8
so the correct graph will be going negative from left to right, and will go through the point (0,-8)
Ok this is an easy one.
-1.5 multiplied by what will get me -1?
Answers
If 15 out of 24 students enjoyed math
yesterday, what percentage of students
did not enjoy math yesterday?
Answers
Answer: 37.5
Step-by-step explanation: 9 students didn't fw math, divide 9 by the total (24) n u get 37.5%
Answer:
Below
Step-by-step explanation:
9 out of 24 did NOT
9/24 = .375 = 37.5 %
David saves $25.78 to buy a video game. After he buys the video game, he has $3.04 leftover. How much does David spend on the video game?
Answers
Answer:
i think it is 22.75 dollars
Step-by-step explanation:
The correct solution set for -7x>_56
Answers
Answer:
Answer in image
Step-by-step explanation:

On the past two quizzes, a student scored a 75 and 83. Write and solve a compound inequality to find the possible values for the 3rd quiz score that would give her an average between 85 and 90, inclusive.
Answers
The possible values for a third quiz score that would give her an average between 85 and 90, inclusive is: 97 ≤ x ≤ 112.
How to determine the average?In Mathematics, the average of these quiz scores can be calculated by using the following formula:
Average = Sum of quiz score/Number of quiz scores
Note: Let the variable q represent the student's score on the third (3rd) quiz.
Substituting the given parameters into the formula, we have the following;
Average = (75 + 83 + q)/3
Average = (158 + q)/3
This ultimately implies that, an average between 85 and 90, inclusive is given by this compound inequality:
85 ≤ (158 + q)/3 ≤ 90
Multiplying all through by 3, we have the following:
255 ≤ (158 + q) ≤ 270
Subtracting 158 from both sides of the inequality, we have the following:
97 ≤ x ≤ 112
Read more on average here: brainly.com/question/878454
#SPJ1
The table shows how many children and adults prefer each of two different fruits. How would you find the joint relative frequency of being an adult who prefers watermelon?%0D%0A%0D%0AWatermelon%09Grapes%09Total%0D%0AChild%09132%0985%09217%0D%0AAdult%09111%09117%09228%0D%0ATotal%09243%09202%09445%0D%0A%0D%0AA.%0D%0ADivide 111 by 228.%0D%0A%0D%0AB.%0D%0ADivide 111 by 243.%0D%0A%0D%0AC.%0D%0ADivide 111 by 445.%0D%0A%0D%0AD.%0D%0ADivide 243 by 445.
Answers
The joint relative frequency is calculated by dividing the frequency of a specific subset (in this case, the number of adults who prefer watermelon) by the total number of data points.
Here, the specific subset is adults who prefer watermelon, which is 111. The total number of data points is the sum of all children and adults, regardless of fruit preference, which is 445.
So, to find the joint relative frequency of being an adult who prefers watermelon, you would divide 111 by 445.
Hence, the correct answer is:
C. Divide 111 by 445.
Selling Price = $ 504 and Gain % = 12%
Answers
Answer:
Step-by-step explanation:
sp = 504
gain = 12%
in this case
sp =100%+12%=504
112%=504
1%=504/112 =4.5
100%=450
so cost =$450
Hope im correct, if i am im glad to be of service.
PLEASE HURRY 100P I REALLY NEED THIS!!!!!

Answers
The range of the data is 30, and the interquartile range (IQR) is 15.
To create a box plot using the given data, we first need to determine the five-number summary, which includes the minimum value, the first quartile (Q1), the median (Q2), the third quartile (Q3), and the maximum value.
From the given data, we can determine the five-number summary as follows:
Minimum: 60
Q1: 70
Median (Q2): 80
Q3: 85
Maximum: 90
Now, let's create a box plot using this information:
```
| | | | |
60 |––––––––|––––––––| |
| | | | |
70 |––––––––|––––––––|––––––––|––––––––|
| | | | |
80 |––––––––|––––––––|––––––––|––––––––|
| | | | |
90 |––––––––|––––––––| |
| | | | |
------------------------------------
60 70 80 90
```
In the box plot, the line within the box represents the median (Q2), the box represents the interquartile range (IQR) from Q1 to Q3, and the lines extending from the box (whiskers) represent the minimum and maximum values. Any data points falling outside the whiskers would be considered outliers.
The range can be calculated as the difference between the maximum and minimum values:
Range = Maximum - Minimum = 90 - 60 = 30
The interquartile range (IQR) is the difference between the third quartile (Q3) and the first quartile (Q1):
IQR = Q3 - Q1 = 85 - 70 = 15
Therefore, the range of the data is 30, and the interquartile range (IQR) is 15.
for more such question on range visit
https://brainly.com/question/30389189
#SPJ8