Answers
Step-by-step explanation:
solve for the value of y in the expression negative 3y minus negative 18
Related Questions
Write the Iogarithmic equation as an exponential equation. (Do not use "..." in your answer.) ln(0.07)=−2.6593.
Answers
The logarithmic equation is to be converted to exponential equation for ln(0.07) = -2.6593 (do not use "..." in your answer).A logarithmic equation is written in the form of logb x = y. This means that `x = by` can be obtained by writing the exponential form of a logarithmic equation.
Where b is the base and y is the exponent on the right-hand side.
The logarithmic equation for the given equation is ln(0.07) = -2.6593.The base of the logarithm is `e` (Euler's number, approx. 2.71828). Using the exponentiation form of the logarithmic equation, `e` can be raised to the power `-2.6593` to obtain the value of `0.07`. Exponential form is written as \(y = b^x\).
This means that by writing the logarithmic form of the exponential equation, x = logb y can be obtained. Where b is the base and y is the number on the right-hand side. The exponential equation for the given logarithmic equation ln(0.07) = -2.6593 is shown below.\(e^-2.6593\) = 0.07
To know more about logarithmic equation this:
https://brainly.com/question/29197804
#SPJ11
HELPPPPPPPPPPPPPPPPPPP

Answers
Answer:
-31
Step-by-step explanation:
8 - ( -5 * - 3 - 1) ÷ 2 - (6)² + 4
8 - (15 - 1) ÷ 2 - 36 + 4
8 - (14) ÷ 2 - 36 + 4
8 - 7 - 36 +4
1 - 36 + 4
-35 + 4 = -31
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Find the volume of the cylinder. Round your answer to the nearest tenth. Use 3.14 for . 7 in. 16 in. The volume of the cylinder is about in?.
Answers
Answer:
1406.7 in^3
Explanation:
The volume of a cylinder with radius r and height h is given by
\(V=\pi r^2h\)Now in our case h = 7 in, r = 16 /2 = 8 in, and in we use pi = 3.14, the above gives
\(V=3.14\cdot8^2\cdot7\)which gives
\(V=3.14\cdot64\cdot7\)\(V=1406.72\text{ in\textasciicircum{}3}\)Rounded to the nearest tenth this is
\(undefined\)
Answer:
The formula to calculate volume of a cylinder is given by the product of base area and its height. Volume of a cylinder = πr2h cubic units.
Step-by-step explanation:
Please help me solve the question from below. It is from IM3 Algebra

Answers
The equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
To determine the solutions to the equation log₂(x - 1) = x³ - 4x, we can set the two expressions equal to each other:
log₂(x - 1) = x³ - 4x
Since we know that the graphs of the two functions intersect at the points (2, 0) and (1.1187, -3.075), we can substitute these values into the equation to find the solutions.
For the point (2, 0):
log₂(2 - 1) = 2³ - 4(2)
log₂(1) = 8 - 8
0 = 0
The equation holds true for the point (2, 0), so (2, 0) is one solution.
For the point (1.1187, -3.075):
log₂(1.1187 - 1) = (1.1187)³ - 4(1.1187)
log₂(0.1187) = 1.4013 - 4.4748
-3.075 = -3.0735 (approx.)
The equation is not satisfied for the point (1.1187, -3.075), so (1.1187, -3.075) is not a solution.
Therefore, the equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
Learn more about Logarithm here:
https://brainly.com/question/30226560
#SPJ1
select the graph that shows the correct sum

Answers
Answer:B
Step-by-step explanation:
The sum of the functions is x²-x-1. Therefore, option B is the correct answer.
What is the graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points. A graph consists of some points and lines between them. The length of the lines and position of the points do not matter.
We are given a graph of a function f(x) as a straight line that passes through (0,2) and (2,0).
Hence, the equation of f(x) is y=-x+2
Also the graph of g(x) is a upward open parabola with vertex at (0,-3)
Hence, the equation of g(x) is y=x²-3
Now the sum function i.e. (f+g)(x) is given by
(f+g)(x)=f(x)+g(x)
= -x+2+x²-3
= x²-x-1
Therefore, option B is the correct answer.
To learn more about the graph visit:
brainly.com/question/14375099.
#SPJ2
answer please. most accurate gets branliest.

Answers
Answer:
m∠U = 36°
m∠V = 75°
m∠T = 69°
Step-by-step explanation:
(2x+14)+(6x+9)+(6x+3)=180
Combine like terms: 14x+26=180
Solve this equation: x=11
Use x=11 to find angles
∠U = 36°
∠V = 75°
∠T = 69°
You can add up all of these measurements to check. =180°
Answer:
The measures of the 3 angles are:Angle T = 69°Angle U = 36°Angle V = 75°Step-by-step explanation:
The Triangle Sum Theorem states that the 3 angles of a triangle must add up to 180°.
We don't know the angles of the triangle, but we do know that the sum of all three unknown angles is 180°.
We set the three expressions together as equal to 180°.
6x + 3 + 6x + 9 + 2x + 14 = 180
Simplify
14x + 26 = 180
Subtract 26
14x = 154
x = 11
Now, we check our answer for x.
6(11) + 3 + 6(11) + 9 + 2(11) + 14 = 180
69 (measure of angle T) + 75 (measure of angle V) + 36 (measure of angle U) = 180
180 = 180 ✅
Note that once we found x, would substitute it in and get the needed measures. Since the needed measures add up to 180°, we know that our answer is correct.
The measures of the 3 angles are:Angle T = 69°Angle U = 36°Angle V = 75°Consider a continuous random variable x, which is uniformly distributed between 65 and 85. The probability of x taking on a value between 75 to 90 is ________. 0.50 0.075 0.75 1.00
Answers
The probability of x taking on a value between 75 to 90 is 0.25.
Given that x is a continuous random variable uniformly distributed between 65 and 85.To find the probability that x lies between 75 and 90, we need to find the area under the curve between the values 75 and 85, and add to that the area under the curve between 85 and 90.
The curve represents a rectangular shape, the height of which is the maximum probability. So, the height is given by the formula height of the curve = 1/ (b-a) = 1/ (85-65) = 1/20.Area under the curve between 75 and 85 is = (85-75) * (1/20) = (10/20) = 0.5Area under the curve between 85 and 90 is = (90-85) * (1/20) = (5/20) = 0.25.
To know more about variable visit:
https://brainly.com/question/15740935
#SPJ11
Jennie drew a scale drawing of her family's game room. The pool table is 4 feet wide in real life. Using a scale of 1 inch: 2 feet, how wide is the pool table in her drawing?
Please answer ASAP.
(Will give brainliest)
Answers
When Jennie drew a scale drawing of her family's game room. If the pool table is 4 feet wide in real life and using a scale of 1 inches: 2 feet, then the width of the pool table in her drawing is 2 inches
The width of the pool table in real life = 4 feet
The scale of width in drawing to real life = 1 inch : 2 feet
Therefore the equivalent ratio is
1 inch : 2 feet :: x inches : 4 feet
1 / 2 = x / 4
x = (1/2) × 4
= 2 inches
Hence, when Jennie drew a scale drawing of her family's game room. If the pool table is 4 feet wide in real life and using a scale of 1 inches: 2 feet, then the width of the pool table in her drawing is 2 inches
Learn more about ratio here
brainly.com/question/13419413
#SPJ1
SOMEONE HELP ME PLEASE AND SHOW WORK

Answers
9x-15=(4x+10)+15
9x-15=4x+25
5x-15=25
5x=40
x=8
Plug in 8 for x:
9x-15
=9(8)-15
=72-15
=57
solve 2x+8<10 or 2x+8>20
Answers
Answer:
1 Add 88 to both sides.
2x=10+8
2x=10+8
2 Simplify 10+810+8 to 1818.
2x=18
2x=18
3 Divide both sides by 22.
x=\frac{18}{2}
x=
2
18
4 Simplify \frac{18}{2}
2
18
to 99.
x=9
x=9
Step-by-step explanation:
2x−8=10
1 Let x=9x=9.
2\times 9-8=10
2×9−8=10
2 Simplify 2\times 92×9 to 1818.
18-8=10
18−8=10
3 Simplify 18-818−8 to 1010.
10=10
10=10
sara chose a date from the calendar. what is the probability that the date she chose is a prime number, given that the date is after the 7th of the month?
Answers
The probability that the date sara chose is a prime number is 0.2.
Given that, sara chose a date from the calendar.
We know that, probability of an event = Number of favourable outcomes/Total number of outcomes.
Here, total number of outcomes = 30
Number of favourable outcomes = 6
Now, probability = 6/30
= 1/5
= 0.2
Therefore, the probability that the date sara chose is a prime number is 0.2.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ1
750% as a decimal mixed number or fraction
Answers
Answer:
750% as a decimal is 7.5
Express each number as a power of a natural number 9
Answers
Answer : Natural numbers include all the whole numbers excluding the number 0. In other words, all natural numbers are whole numbers, but all whole numbers are not natural numbers. Natural Numbers = {1,2,3,4,5,6,7,8,9,…..}
Which of the following is the equation for the graph shown?

Answers
Answer:
x equals 0
Step-by-step explanation:
it is a vertical line on zero and this is 1st grade level math
Find the mean of the set of data.
3,2, 9, 3, 8,4,5,8,9, 2
Answers
Answer:
5.3
Step-by-step explanation:
To find the mean you must add up all the numbers in the set then divide them by the number of numbers in said set.
Answer:
Hi! The answer to your question is 5.3
Step-by-step explanation:
☆*: .。..。.:*☆☆*: .。..。.:*☆☆*: .。..。.:*☆☆*: .。..。.:*☆
☆Brainliest is greatly appreciated!☆
Hope this helps!!
- Brooklynn Deka
The diameter of a circle is 46 yards. What is the circle's circumference? d=46 yd Use 3.14 for n.

Answers
Answer:
144.44 yards
Step-by-step explanation:
The formula to find circumference is: C = π · d
Since we already have most of the factors figured out, we just replace them with what we have.
C = 3.14 · 46 yrds
144.44 = 3.14 · 46
a student has scores of 84%, 71%, 86%, and 73% on four exams. what grade does the student need on the next exam to have an overall mean of 80%?
Answers
Answer:
Step-by-step explanation:
So, first you add the four exam percentage which will be 314 then you multiply 80 and 5. We use 5 because there are total 5 exams which will give the mean of 80%. After you get the answer for 80x5 which will be 400. Then you do, 400 - 314 which will be 86. So, the answer is 86%. To figure out if that answer is right, You add all the scores percentage and divide that by 5 and you should get 80%.
To have an overall mean of 80% after five exams, the student needs to score 88% on the next exam.
To find the student's overall mean, we need to add up all the scores and divide by the number of exams.
We have 4 exams scores:84%, 71%, 86%, and 73%.
Therefore, the total of the four exam scores is:
84% + 71% + 86% + 73% = 314%
To find the overall mean after five exams, the total score after five exams should be 5 × 80% = 400%.
Therefore, to have an overall mean of 80%, the student must score (400 - 314)% on the fifth exam, which is equivalent to: 86%.
Hence, the student needs to score 86% on the next exam to have an overall mean of 80%.
To learn more about Mean visit:
https://brainly.in/question/15476192
#SPJ1
Let consider a biased coin that has a probability í = 3/4 of coming up heads. If I pay you $1 if it comes up heads and $2 if it comes up tails. Let í be the number of dollars I pay you, which is a random variable. What is the expected value of í when the biased is flipped once?
Answers
The probability of heads is 3/4, and the probability of tails is 1/4. Let í be the number of dollars that you receive, which is a random variable. If it comes up heads, you will receive $1, and if it comes up tails, you will receive $2.
Thus, the possible values of í are 1 and 2.The expected value of í is given by the formula below:
\(E(i) = \sum_{i=1}^n x_i P_i\)
Where xi is the ith possible value of í, and Pi is the probability of xi. The expected value of í is given by the formula below:
\(E(i) = \sum_{i=1}^n x_i P_i\)
For this example, the possible values of í are 1 and 2. The probability of heads is 3/4, and the probability of tails is 1/4. Therefore, we can calculate the expected value of í as follows:
\(E(i) = (1) \cdot \frac{3}{4} + (2) \cdot \frac{1}{4}\)
\(= \frac{3}{4} + \frac{2}{4}\)
\(= \frac{5}{4}\)
Thus, the expected value of í when the biased coin is flipped once is $1.25.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Given m||n, find the value of x.
(2x+9)
(7X+24)
Answers
Given, 9−7x=5−3x
Given, 9−7x=5−3xPut x terms on one side and constants on another side.
Given, 9−7x=5−3xPut x terms on one side and constants on another side.⇒9−5=7x−3x
Given, 9−7x=5−3xPut x terms on one side and constants on another side.⇒9−5=7x−3x⇒4=4x
Given, 9−7x=5−3xPut x terms on one side and constants on another side.⇒9−5=7x−3x⇒4=4x⇒x= 4/4 =1
=1Hence, required solution is x=1.
please mark me a brainlist answer I need only 1 ok
Factor by gcf 6x2+3x+21 The 2 is supposed to be small.
Pleaseeee
Answers
Answer:
6x^2 + 3x + 21 = 3(2x^2 + x + 7)
Step-by-step explanation:
We have this as follows;
6x^2 + 3x + 21 = 3(2x^2 + x + 7)
The quadratic trinomial inside the bracket cannot be factored any further
so we have the present form as the correct answer
Please help me asap!!

Answers
Answer:
D
Step-by-step explanation:
Hello I would deeply appreciate any help and hello its my birthday :))
Which statements about the graph of the exponential function f(x) are TRUE? Select all that apply.
Question 6 options:
The x-intercept is 2.
The y-intercept is 3.
The asymptote is y = -1
The range is all real numbers
The domain is all real numbers.
f(x) is positive for all x-values less than 1
As x increases, f(x) approaches, but never reaches, -1.

Answers
Im not sure about the last two sorry
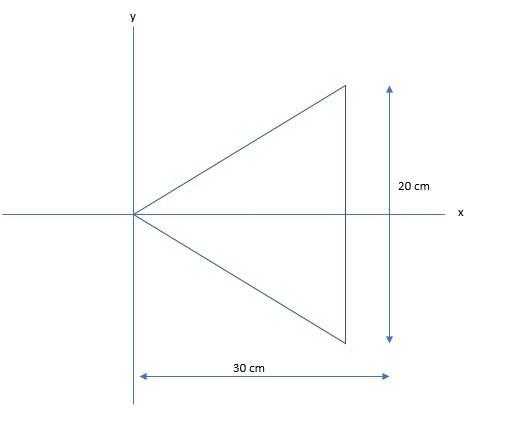
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

Solve for all solutions in [0, 2]: since=1/2
Answers
The solutions for sin(x) = 1/2 in the interval [0, 2π] are approximately π/6, 13π/6, 5π/6, and 17π/6.
To solve the equation sin(x) = 1/2 in the interval [0, 2π], we can use the unit circle and the values of the sine function for the common angles.
We are given the equation sin(x) = 1/2.
The sine function represents the y-coordinate of a point on the unit circle. The value of 1/2 corresponds to the y-coordinate of the point (1/2, √3/2) on the unit circle.
We need to find the angles whose sine value is 1/2. From the unit circle, we know that the angles 30° and 150° have a sine value of 1/2.
However, we are given that the solutions should be in the interval [0, 2π]. To find the corresponding angles in this interval, we can add or subtract multiples of 2π.
The angle 30° corresponds to π/6 radians, and the angle 150° corresponds to 5π/6 radians.
Adding multiples of 2π to π/6 and 5π/6, we can find all the solutions within the given interval:
π/6 + 2πk, where k is an integer
5π/6 + 2πk, where k is an integer
We need to ensure that the solutions are within the interval [0, 2π]. Therefore, we consider the values of k that satisfy this condition.
For π/6 + 2πk:
k = 0 gives π/6
k = 1 gives 13π/6
For 5π/6 + 2πk:
k = 0 gives 5π/6
k = 1 gives 17π/6
Therefore, the solutions for sin(x) = 1/2 in the interval [0, 2π] are approximately π/6, 13π/6, 5π/6, and 17π/6.
To learn more about sine function click here:
brainly.com/question/12015707
#SPJ11
The angle measures for -8π ≤ θ ≤ -4π that satisfy cos(θ) = -0.5 are approximately -2.0944 radians and -7.2355 radians.
To determine the values of the argument that make the given trigonometric equations true, we can use the properties and periodicity of the trigonometric functions.
i. For the equation cos(θ) = -0.5, where 0 ≤ θ ≤ 2π:
We need to find the values of θ that satisfy this equation within the given domain.
Since cosine is negative in the second and third quadrants, we can find the reference angle by taking the inverse cosine of the absolute value of -0.5:
Reference angle = arccos(0.5) ≈ 1.0472 radians
In the second quadrant, the angle with a cosine value of -0.5 is the reference angle plus π:
θ = π + 1.0472 ≈ 4.1888 radians
In the third quadrant, the angle with a cosine value of -0.5 is the reference angle minus π:
θ = -π - 1.0472 ≈ -4.1888 radians
Therefore, the values of θ that satisfy cos(θ) = -0.5 within the given domain are approximately 4.1888 radians and -4.1888 radians.
ii. For the equation α ± πn, where n is any integer:
The equation α ± πn represents the general solution for any possible value of the argument α. The ± sign indicates that the value can be either positive or negative.
This equation allows us to find all possible values of the argument by adding or subtracting integer multiples of π.
iii. For the equation α ± 2πn, where n is any integer:
Similar to the previous equation, α ± 2πn represents the general solution for any possible value of the argument α. The ± sign indicates that the value can be either positive or negative.
This equation allows us to find all possible values of the argument by adding or subtracting integer multiples of 2π.
To find the angle measures for -8π ≤ θ ≤ -4π that satisfy the equation cos(θ) = -0.5, we can use the same approach as in part (i):
Reference angle = arccos(0.5) ≈ 1.0472 radians
In the second quadrant, the angle with a cosine value of -0.5 is the reference angle plus π:
θ = -π + 1.0472 ≈ -2.0944 radians
In the third quadrant, the angle with a cosine value of -0.5 is the reference angle minus π: θ = -2π - 1.0472 ≈ -7.2355 radians
To learn more about trigonometric functions click here:
brainly.com/question/25618616
#SPJ11
select all of the expressions that are equivalent to 4(5x+2y)
Answers
Answer:
Where are the expressions?
Step-by-step explanation:
Answer:
Step-by-step explanation:
please help 2 questions


Answers
Answer:
1) 2002
2) 92
Step-by-step explanation:
1)
First, you need to find the area of the triangular base. The height of the triangle is 7, and the base is 26, meaning that the area is 7*26/2=91. Multiplying this by the length of the prism, you get 2002 cubic meters.
2)
First, you need to find the area of the trapezoidal base. The two bases of the trapezoid have lengths 12 and 11, while the height is 8, meaning that the area is 8*(12+11)/2=92 cubic centimeters.
Hope this helps!
A truck is 20cm long on a scale drawing. The scale is 1cm = 50cm (1:50). How long is the truck in real life?
Answers
Answer:
1000
Step-by-step explanation:
20x50
A line has a slope of 2 and a y -intercept of 2. What is its equation in slope -intercept form?
Answers
Here is the equation you need. I’m 95% sure this is correct.
slope intercept form: y= mx + b
m=slope
b=y-intercept
hope this helps
The objective of keyword bidding is to: a.obtain the most profitable domain name. b.limit the amount of money the firm spends on search marketing. c.always be ranked first. d.get the best ranking for the lowest cost.
Answers
The objective of keyword bidding is to d. get the best ranking for the lowest cost.
Keyword bidding is a practice used in online advertising, specifically in pay-per-click (PPC) campaigns, where advertisers bid on specific keywords to display their ads in search engine results. The objective of keyword bidding is to achieve the best possible ranking for their ads while keeping the cost as low as possible.
Option (a), obtaining the most profitable domain name, is not related to keyword bidding. Domain names refer to the website address or URL and are not directly associated with keyword bidding.
Option (b), limiting the amount of money the firm spends on search marketing, is partially correct but not the primary objective. While controlling costs is important, the main goal of keyword bidding is to optimize the ranking and visibility of ads.
Option (c), always being ranked first, is not feasible for every advertiser. Search engine rankings are determined by various factors, including bid amount, quality score, and relevance. It is not guaranteed that an advertiser will always secure the top position.
Learn more about Keyword bidding here:
https://brainly.com/question/9381008
#SPJ11
can you apply the properties of rational exponents to an example?
Answers
We can simplify \((16x^4)^(-1/2) to 1/(4x^2)\) using the properties of rational exponents.
Certainly! Here's an example:
Simplify the expression: \((16x^4)^(-1/2)\)
We can apply the property of rational exponents which states that \((a^m)^n = a^(m*n)\). Using this property, we get:
\((16x^4)^(-1/2) = 16^(-1/2) * (x^4)^(-1/2)\)
Next, we can simplify \(16^(-1/2)\) using the rule that \(a^(-n) = 1/a^n\):
\(16^(-1/2) = 1/16^(1/2) = 1/4\)
Similarly, we can simplify \((x^4)^(-1/2)\) using the rule that \((a^m)^n = a^(m*n)\):
\((x^4)^(-1/2) = x^(4*(-1/2)) = x^(-2)\)
Substituting these simplifications back into the original expression, we get:
\((16x^4)^(-1/2) = 1/4 * x^(-2) = 1/(4x^2)\)
Therefore, the simplified expression is \(1/(4x^2).\)
Learn more on rational exponents here
brainly.com/question/20726608
#SPJ1
