Answers
Answer:
Yes. The shown graph shows a linear graph because the points are a strong correlation which makes a trend line.
Step-by-step explanation:
Hoped this helped.
Related Questions
A salesman has scheduled two appointments to sell encyclopedias. His first appointment will lead to a sale with probability 0.3, and his second will lead independently to a sale with probability 0.6. Any sale made is equally likely to be either for the deluxe model, which costs $1000 or the standard model, which costs $500.
Answers
The probability that the salesman sells a deluxe and a standard encyclopedia on his two appointments is 0.126.
To calculate this probability, we can use the multiplication rule of probability, which states that the probability of two independent events occurring together is the product of their individual probabilities.
Let S1 be the event that the salesman makes a sale on his first appointment, and S2 be the event that he makes a sale on his second appointment. Let D1 be the event that the sale is for the deluxe model, and S1 be the event that the sale is for the standard model.
Then, the probability of selling a deluxe model on the first appointment is 0.3 * 0.5 = 0.15 (since there is a 50% chance of selling a deluxe model). The probability of selling a standard model on the second appointment is 0.4 * 0.5 = 0.3 (since there is a 50% chance of selling a standard model).
Therefore, the probability of selling a deluxe model on the first appointment and a standard model on the second appointment is 0.15 * 0.3 = 0.045. However, this can also occur in reverse order (i.e., selling a standard model on the first appointment and a deluxe model on the second appointment), so we need to double the probability to get the final answer: 0.045 * 2 = 0.09.
Finally, the probability that both events occur (selling a deluxe and a standard encyclopedia on his two appointments) is 0.09 * 2 = 0.126.
For more questions like Probability visit the link below:
https://brainly.com/question/13285296
#SPJ11
A commercial jet flies 1,500 miles with the wind. In
the same amount of time it can fly 1,000 miles against the
wind. The speed of the jet in still air is 550 mph. Find the
speed of the wind.
Answers
Answer:
As below
Step-by-step explanation:
we want to know how long it took to fly so make two equations and set them equal to each other using the variable t
so, use d = r*t where d= distance , r= rate ( speed) and t = time
w= wind velocity (speed with direction)
1500=(w+550)*t
1000=(-w+550)*t
now make both equations with respect to t
1500/(w+550) = t
1000/(-w+550) = t
since they are both equal to t, where t is the same amount of flying time, set the two equations equal to each other
1500/(w+550) = 1000/(-w+550)
now solve for w
1500w + 825,000 = -1000w+550,000
2500w= -275,000
w = - 110
the wind speed is 110 opposite of the planes direction but also, if the plane flies in the other direction with it.
wind velocity (velocity is speed with a direction ) is 110 MPH
they are asking for speed, b/c we don't know anything about direction... that is which direction is the plane headed during it's flight therefore we also can't say anything about the wind direction either. :|
a unit vector is a vector with length . the length of a vector is also called its norm. given any vector what is the unit vector pointing in the same direction as ? answer in terms of and the norm of the vector . (type x for the vector , and norm(x) for the norm of the vector .)
Answers
The answer in terms of x and the norm of the vector is: x / norm(x)
The unit vector pointing in the same direction as vector x can be calculated as:
x / ||x||
where ||x|| represents the norm (length) of the vector x.
x / norm(x)
In mathematics, a vector is an object that has both magnitude and direction. It can be represented by an arrow, where the length of the arrow represents the magnitude of the vector, and the direction of the arrow represents the direction of the vector. Vectors can be represented in different coordinate systems such as Cartesian, polar, or spherical coordinates.
In linear algebra, vectors are often represented as n-tuples of real numbers, where n is the dimension of the vector space. For example, a 2-dimensional vector can be represented as (x, y), and a 3-dimensional vector can be represented as (x, y, z). Vectors can be added and subtracted, scaled by a scalar, and used in operations such as dot product and cross product.
For more such questions on unit vector
https://brainly.com/question/15525590
#SPJ4
How to solve adjacent angles?

Answers
Answer:
D
Step-by-step explanation:
1 + 4x and 57° are corresponding angles and are congruent , so
1 + 4x = 57 ( subtract 1 from both sides )
4x = 56 ( divide both sides by 4 )
x = 14
Find the standard deviation of the sampling distribution of sample means using the given information. Round to one decimal place, if necessary. μ = 64 and o = 12; n = 9
Answers
The standard deviation of the data sample is 2.55.
What is the standard deviation of the data sample?The standard deviation of the data sample is calculated by applying the following formula;
S.D = √ (x - μ)²/(n - 1)
where;
μ is the mean of the distributionx is the sample datan is the number of sample dataThe given parameters;
mean, μ = 64
x, = 12
number of samples = 9
The standard deviation of the data sample is calculated as;
S.D = √ (12 - 64)²/(9 - 1)
S.D = 2.55
Thus, the standard deviation of the data sample is calculated by applying the formula for standard deviation.
Learn more about standard deviation here: https://brainly.com/question/24298037
#SPJ1
Two boards are placed end to end to make a walkway. One board is 6 feet 11 inches long, and the other board is 5 feet 7 inches long. How long is the walkway?
Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
The walkway is 11 feet 6 inches long.
To find the length of the walkway, we need to add the lengths of the two boards.
The first board is 6 feet 11 inches long, which can be written as 6 + 11/12 feet using the fact that there are 12 inches in a foot.
The second board is 5 feet 7 inches long, which can be written as 5 + 7/12 feet.
Now we can add the lengths of the two boards:
6 + 11/12 feet + 5 + 7/12 feet
= 11 + 6/12 feet
=11 + 1/2 feet
Therefore, the walkway is 11 feet 6 inches long.
To learn more on Coordinate Geometry click:
brainly.com/question/27326241
#SPJ1
What is the component form and magnitude of the vector? LeftAngleBracket 3, negative 2 RightAngleBracket and StartRoot 13 EndRoot LeftAngleBracket 3, negative 2 RightAngleBracket and StartRoot 5 EndRoot LeftAngleBracket negative 3, 2 RightAngleBracket and StartRoot 13 EndRoot LeftAngleBracket negative 3, 2 RightAngleBracket and StartRoot 5 EndRoot
Answers
Answer:
C
Step-by-step explanation:
edg 2023
Which of the following conditions is/are NOT necessary to justify the use of t procedures in a significance test for the slope of a regression line?
For each given value of x, the values of the response variable y are Normally distributed.
For each given value of x, the values of the response variable y are independent.
For each given value of x, the mean of y is the same.
I
II
I and II
III
I and III
Answers
The condition that is not necessary to justify the use of t procedures in a significance test for the slope of a regression line is III. For each given value of x, the mean of y is the same.
We have to identify the unnecessary conditions to justify the use of t procedures in a significance test for the slope of a regression line.
I) The first condition is that for each given value of x, the values of the response variable y are normally distributed. This condition is necessary.
II) The second condition is that for each given value of x, the values of the response variable y are independent. This is a vital condition.
III) The third condition is that for each given value of x, the mean of y is the same. This is a condition that need not be true.
To learn more about regression line, visit :
https://brainly.com/question/7656407
#SPJ1
Write a positive or negative integer that represent the situation?

Answers
Answer:
A or -24
Step-by-step explanation:
if your in debt its -24
What is the circumference of a circle with a radius of 21 feet? Use 22 over 7 for π.
132 feet
66 feet
5,544 feet
1,386 feet
Answers
The circumference of a circle whose radius is 21 feet, is 132 feet, thus the first option is the correct one.
How to get the circumference of the circle?We know that for a circle of radius R, the circumference is given by:
C = 2*π*R
Where π = 22/7
And here we know that the radius is 21 feet, then we can replace that in the formula above and we will get:
C = 2*(22/7)*21 feet = 132 feet
The circumference of that triangle is 132 feet, thus, the correct option is the first one.
Learn more about circles by reading:
https://brainly.com/question/1559324
#SPJ1
Which expression below gives the average rate of change of the function h(x) = 4^x+2 + 7 on the interval –3 ≤ x ≤ 5?
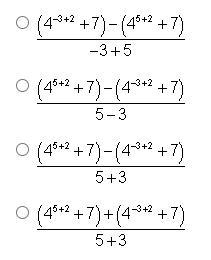
Answers
Answer:
4^(5+2) + 7 - (4^(-3+2) +7)
--------------------------------------
5 +3
Step-by-step explanation:
The average rate of change is given by
h(5) - h(-3)
---------------
5 - -3
h(5) - h(-3)
---------------
5 +3
h(5) = 4^(5+2) + 7
h(-3) = 4^(-3+2) +7
4^(5+2) + 7 - (4^(-3+2) +7)
---------------
5 +3
Answer: i got the answer c. Good luck!
The correct mix for a batch of concrete is 6:3:2 in terms of sand, gravel and cement. The batch is to have 3300 pounds of these ingredients. How many of each are needed?
pounds of sand
pounds of gravel
pounds of cement
Answers
Answer:
1,800 lbs of sand
900 lbs of gravel
600 lbs of cement
Step-by-step explanation: 11*300=3,300. 300*6=1,800, 300*3=900, and 300*2=600. This is correct because if you add 1,800+900+600 you get 3,300.
Analyze the diagram below and complete the instructions that follow.
8
45°
Find the value of x.
A. 4
B. 8√√2
2
C. 4√2
DG
45°
Save and Exit
Next
Subr

Answers
Answer:
Based on the diagram, we can see that the triangle formed by the line segment with length 8 and the two dashed line segments is a right triangle with a 45° angle. This means that the other two angles of the triangle are also 45° each.
Using the properties of 45°-45°-90° triangles, we know that the length of the hypotenuse is equal to the length of either leg times the square root of 2. Therefore, we have:
x = 8 / sqrt(2) = 8 * sqrt(2) / 2 = 4 * sqrt(2)
So the value of x is option B: 8√2 / 2 or simplified, 4√2.
If every 2 cm on a scale drawing is equal to 7 feet in real life, which lines on the drawing would be greater than 21 feet in real life? Select all that apply. A) 7 cm B) 5 cm C) 9 cm D) 12 cm
Answers
The correct answers are A) 7cm, C) 9cm and D) 12cm
Define the Conversion of units?The process of changing a given quantity that is expressed in one unit of measurement to another unit of measurement that is equivalent in value is referred to as conversion of units.
If every 2 cm on a scale drawing is equal to 7 feet in real life, then we can use proportions to find out which lines on the drawing would be greater than 21 feet in real life.
Let x be the length of a line on the scale drawing in centimeters. Then, we can set up the following proportion:
⇒ \(\frac{2cm}{7 feet} = \frac{x cm }{yfeet}\)
where y is the length of the line in real life. Solving for y, we get:
⇒ \(y = \frac{7 feet} {2cm} *x\)
⇒ \(y = 3.5 x feet\)
If we put x = 2cm (given) then, y = 7 feet
For y = 21 feet, the value of x = 6cm.
Therefore, any line on the scale drawing that is greater than 6cm in length corresponds to a length greater than 21 feet in real life.
So, the lines on the drawing that are greater than 21 feet in real life are:
A) 7cm, C) 9cm, D) 12cm
Therefore, the correct answers are A) 7cm, C) 9cm and D) 12cm
To know more about conversion, visit:
https://brainly.com/question/13016491
#SPJ1
what is −2(x+6)=4x
x=
Answers
Answer:
x=-2
Step-by-step explanation:
Distribute, add 12 to both side, then simplify
Answer: -2
Let's solve your equation step-by-step.
−2(x+6)=4x:
Step 1: Simplify both sides of the equation.
−2(x + 6) = 4x
(−2)(x) + (−2)(6) = 4x (Distribute)
−2x + (−12) = 4x
−2x − 12 = 4x
Step 2: Subtract 4x from both sides.
−2x − 12 − 4x = 4x − 4x
−6x − 12 = 0
Step 3: Add 12 to both sides.
−6x − 12 + 12 = 0 + 12
−6x = 12
Step 4: Divide both sides by -6.
−6x/−6 = 12/−6
x = −2
What is 0.2105 rounded to the nearest hundredth
Answers
Answer:
Step-by-step explanation: 0.21
Answer:
Step-by-step explanation: 0 is the ones place 2 would be the tenths and 1 the hundreths when rounding you use the fact of if the number following is 5 or more you round up 4 or less it stays the same so the answer is 0.21find the standard deviation of binomial random variable. A die is rolled 18 times and the number of fours that comes up is tallied
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
The standard deviation is \(\sigma =1.5811\)
Step-by-step explanation:
The sample size is n = 18
Generally the probability of getting a four in the toss of the fair die is mathematically represented as
\(p = \frac{1}{6 }\)
While the probability of not getting a four is
\(q = 1 - p\)
\(q = 1 - \frac{1}{6}\)
\(q = \frac{5}{6}\)
Now the standard deviation for the binomial random number is mathematically represented as
\(\sigma = \sqrt{n * pq }\)
substituting values
\(\sigma = \sqrt{18 * \frac{1}{6}* \frac{5}{6} }\)
\(\sigma =1.5811\)

how much money deposited now will provide payment of Rs. 15000 at the end of each half year for 10 years, if interest is 16% compounded six-monthly
Answers
The interest is 16% compounded semi-annually, is Rs. 121,179.10.
To determine how much money needs to be deposited now to provide a payment of Rs. 15,000 at the end of each half year for 10 years, we will use the formula for the present value of an annuity.
Present value of an annuity = (Payment amount x (1 - (1 + r)^-n))/rWhere:r = interest rate per compounding periodn = number of compounding periodsPayment amount = Rs. 15,000n = 10 x 2 = 20 (since there are 2 half years in a year and the payments are made for 10 years)
So, we have:r = 16%/2 = 8% (since the interest is compounded semi-annually)Payment amount = Rs. 15,000Using the above formula, we can calculate the present value of the annuity as follows:
Present value of annuity = (15000 x (1 - (1 + 0.08)^-20))/0.08 = Rs. 121,179.10Therefore, the amount that needs to be deposited now to provide payment of Rs. 15,000 at the end of each half year for 10 years, if the interest is 16% compounded semi-annually, is Rs. 121,179.10.
For more such questions on semi-annually
https://brainly.com/question/30573341
#SPJ8
what type of data would best be displayed in a box plot
Answers
Answer:(2x+7)+(2x+7)
Step-by-step explanation:
what you do is put 2x on the top and on the side and then seven on the top and on the side and then you got your answer
mark needs to move figure one so it overlaps figure two in exactly two transformation his first transformation is to reflect about the x-axis what should his second be
Answers
Answer:
C. Rotate 180° clockwise about the origin.
Step-by-step explanation:
A rectangular sheet of metal measures 8 inches by 10 inches. The metal is worth $3.00 per
square inch. How much is the sheet of metal worth?
Answers
Answer:
240$$
Step-by-step explanation:
find the area
A=LW
A=8x10
A=80
80x3=240
Please help, include work if possible please and thank you :)

Answers
screenshot shows the answer x=4 and x= 2

In what time will a sum of
money double itself at 9% per
year if interest is calculated
annually?
Please explain step by step to help me understand and be able to do this on my own in the future
Answers
It will take 9 years to double the money at 9% per annum
What is Compound Interest?Compound interest, also known as interest on principal and interest, is the practice of adding interest to the principal amount of a loan or deposit.
Given:
let P = 100
Interest = 100
Apply formula of interest
Interest= (P x R x T) ÷ 100
100= (100x 9 xT )÷100
T= 11.11 years
In case of annually compounded interest let us assume that Rs 100 to\((1.09)^ 9 =(1.09)^T\) become 200 . Apply formula
A=P\((1+R/100)^T\)
200=100 \((1+9/100)^T\)
200=100 \((109/100)^T\)
2 = \((109/100)^T\)
\((1.09)^ 9 =(1.09)^T\)
On Comparing
T= 9 years.
Hence, It will take 9 years.
Learn more about Compound Interest here:
https://brainly.com/question/14295570
#SPJ1
find the quadratic polynomial, the sum of whose zeroes is 8 and their product is 12. hence, find the zeroes of the polynomial.
Answers
The required quadratic polynomial is \(x^{2} - 8x + 12 =0\) and roots of this quadratic polynomial are 2 and 6.
Let the roots of the quadratic equation be \(\alpha\) and \(\beta\) .
Given,
Sum of zeroes, \(\alpha +\beta = 8\)
Product of Zeroes, \(\alpha *\beta = 12\)
we know that,
Quadratic Equation can be written as :
\(x^{2} - (\alpha + \beta )x + \alpha \beta =0\)
Substituting the values in the above Equation,
\(x^{2} - (8)x + (12) =0\)
\(x^{2} - 8x + 12 =0\)
Hence, The required quadratic equation is \(x^{2} - 8x + 12 =0\) .
Now, let's factorize the equation to find its root:
\(x^{2} - 8x + 12 =0\)
\(x^{2} - 6x -2x+ 12 =0\)
\(x(x-6) -2(x-6)=0\)
\((x-6)(x-2)=0\)
⇒ \(x= 2,6\)
Therefore roots of the quadratic equation \(\alpha ,\beta\) are \(2,6\) .
Learn more about Quadratic Equation:
https://brainly.com/question/30098550
#SPJ4
Use mathematical induction to prove 2^n>=2n is true for all positive integers.
Answers
By the Principle of Mathematical Induction, 2ⁿ≥2n is true for all positive integers.
The given inequality is 2ⁿ≥2n.
Let n = 1
2^1 ≥ 2^1
2 ≥ 2 which is true
Inductive Step: Assume 2ⁿ≥2n is true for some arbitrary positive integer k.
We need to prove that 2^(k+1) ≥ 2^(k+1)
2^(k+1) ≥ 2*2^k (by the inductive hypothesis)
2^(k+1) ≥ 2*2^(k+1)
2^(k+1) ≥ 2^(k+1) which is true
Therefore, by the Principle of Mathematical Induction, 2ⁿ≥2n is true for all positive integers.
To learn more about the inequalities visit:
https://brainly.com/question/20383699.
#SPJ1
2x + = x + 5
Solve using a mental strategy
Answers
The required solution of the given equation is 5.
What is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign. Equation, statement of equality between two expressions consisting of variables and/or numbers.
Given:
The given equation is
2x + = x + 5
According to given question we have
Mental Math is an exercise where we solve mathematical equations mentally without the help of a calculator.
To do the bigger or important quantities first. This gives an estimate of the value expected. Such an approach is front end or left to right multiplication.
2x = x + 5
Substract x from both sides we get,
x=5
Therefore, the required solution of the given equation is 5.
Learn more details about equation here:
https://brainly.com/question/10413253
#SPJ1
How many solutions exist for the given equation?
12×+1=3(4×+1)-2
Answers
Answer:
infinite Solutions
Step-by-step explanation:
12x+1 = 12x+3-2
12+1 = 12x+1
The equation is same on both sides, so x can be anything.
Answer:
infinite solutions
Step-by-step explanation:
12x+1=3(4x+1)-2
Distribute
12x+1 = 12x+3 -2
Combine like terms
12x+1 = 12x+1
Subtract 12x from each side
12x+1-12x = 12x+1-12x
1 =1
Since this always true, there are infinite solutions
Find the distance between the points (10,5) and (6,2)
Answers
The answer fam is........... 5 To find the distance between (10,5) and (6,2) use the "Distance formula"
you want to reach $3,000 in savings over four years your account will earn 10% interest per year how much must you save each month
Answers
You would need to save approximately $56.62 each month to achieve your savings goal of $3,000.00 over four years.
To calculate the monthly savings required to reach a savings goal of $3,000.00 over four years with a 10% annual interest rate, we can use the PMT (Payment) function.
The PMT function helps us determine the fixed payment amount needed to achieve a specific future value within a given time frame.
Let's break down the given information:
Present Value (PV): $0.00 (initial account balance)
Future Value (FV): $3,000.00 (savings goal)
Interest Rate (rate): 10% per year (annual interest rate)
Number of Periods (nper): 4 years (48 months)
Using the PMT function, we need to plug in the values and solve for the monthly payment (savings amount).
The formula for the PMT function is:
PMT(rate, nper, pv, [fv], [type])
Where:
rate = Interest rate per period
nper = Total number of periods
pv = Present value (initial account balance)
fv = Future value (savings goal)
type = (Optional) Indicates whether the payment is made at the beginning (1) or end (0) of the period.
We'll assume 0 for monthly savings.
Let's calculate the monthly savings using the PMT function:
PMT(10%/12, 4*12, 0, -3000, 0)
Here, we divide the annual interest rate by 12 to get the monthly interest rate (10%/12), multiply the number of years by 12 to get the total number of months (4*12), set the initial account balance (pv) as $0, set the future value (fv) as -$3,000 (negative because it's an outgoing payment), and assume the savings are made at the end of each month (type = 0).
Using a financial calculator or spreadsheet software, the monthly savings required to reach the goal of $3,000.00 over four years with a 10% annual interest rate is approximately $56.62.
Therefore, you would need to save approximately $56.62 each month to achieve your savings goal of $3,000.00 over four year.
For similar question on annual interest rate.
https://brainly.com/question/29059795
#SPJ11
Question : you want to reach $3,000.00 in savings over four years. Your account will earn 10% interest per yea Initially your account has a zero balance. How much must you save each month to achieve this goal? Use the PMT() function. Look it up in the e-book if you do not know how to use it. TIP: This is monthly so do not forget to adjust the interest rate and number of payment.
Which pair of numbers has a GCF of 5? A.15 and 30 C.45 and 9 B.5 and 21 D.20 and 55
Answers
Answer:
D
Step-by-step explanation:
The GCF in answer choice A is 15.
The GCF in answer choice B is none.
The GCF in answer choice C is 9 since 45 is divisible by 9 and 9 is divisible by itself
D is correct as 55/5 = 11 and cannot be divided anymore. And 20 is divisible by 5
