is the following a power function, a polynomial, both, or neither? f(x)=−x−4‾‾‾‾‾‾‾√
Answers
The function f(x) = -√(x - 4) is a power function but not a polynomial.
To find whether the function f(x) = -√(x - 4) is a power function, a polynomial, both, or neither.
The function f(x) = -√(x - 4) is a power function since it can be written in the form f(x) = x^n, where n is a real number. In this case, n = 1/2, so the function is f(x) = -(x - 4)^(1/2).
However, f(x) = -√(x - 4) is not a polynomial because polynomials are functions with the form f(x) = a_nx^n + a_(n-1)x^(n-1) + ... + a_1x + a_0, where a_n, a_(n-1),..., a_1, and a_0 are constants and n is a non-negative integer. Since the exponent in f(x) = -√(x - 4) is 1/2 (a non-integer), it is not a polynomial.
In conclusion, f(x) = -√(x - 4) is a power function but not a polynomial.
Learn more about power function:
https://brainly.com/question/24364138
#SPJ11
Related Questions
Mrs.baxter deposits 2000 into an account that earns 5% simple interest how much is mrs baxters investment worth after 8 years What formula should be used
Answers
Answer: The formula to calculate simple interest is:
I = P * r * t
where:
- I is the interest earned
- P is the principal amount (the initial investment)
- r is the annual interest rate (as a decimal)
- t is the time in years
- To calculate the total amount in the account after the interest is earned, you need to add the interest earned to the principal amount.
So for Mrs. Baxter's investment, the calculation would be:
P = 2000 (the principal)
r = 0.05 (the annual interest rate as a decimal)
t = 8 (the time in years)
I = P * r * t = 2000 * 0.05 * 8 = 800
The interest earned over the 8-year period is $800.
The total amount in the account after 8 years would be the principal plus the interest earned:
A = P + I = 2000 + 800 = 2800
So Mrs. Baxter's investment would be worth $2,800 after 8 years.
Step-by-step explanation:
The amount after 8 years with the rate of interest as 5% simple interest is $2800.
What is meant by simple interest?
Simple interest is a way to figure out how much interest will be charged on a sum of money at a specific rate and for a specific duration of time. Unlike compound interest, where we add the interest of one year's principal to the next year's principal to compute interest, the principal amount under simple interest remains constant. Simple interest is a quick and simple approach to figuring out how much money has accrued interest. Interest is always applied to the original principal amount and is calculated at the same rate for each period of time.
Given,
The principal amount P = $2000
The rate of interest r = 5% = 5/100 = 0.05
The time period t = 8 years.
We have to find the amount after 8 years using simple interest formula.
Amount A = P(1+rt) = 2000(1+0.05 * 8)
= 2000 * 1.4 = $2800.
Therefore the amount after 8 years with the rate of interest as 5% simple interest is $2800.
To learn more about the simple interest, follow the link.
https://brainly.com/question/25793394
#SPJ1
Select all the expressions that have a value of 96 when s=4.
Answers
1. s + s + s + s + s + s + s + s = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
2. 12 × s - 48 = 12 × 4 - 48 = 48 - 48 = 0
3. (s + 10) × s - s = (4 + 10) × 4 - 4 = 14 × 4 - 4 = 56 - 4 = 52
4. 2 × s × s × s × s = 2 × 4 × 4 × 4 × 4 = 2 × 64 = 128
5. (s + 6) × (s + 2) = (4 + 6) × (4 + 2) = 10 × 6 = 60
The only expression that has a value of 96 for s=4 is not on this list.
1. (a) The sum of two numbers is 17. The difference between twice the larger number and three times the smaller is 4. Find the numbers
Answers
Answer:
Denoting 2 desired numbers: x and y, then:
x + y = 17
2x = 3y + 4
<=>
x = 17 - y
2*(17 - y) = 3y + 4
<=>
x = 17 - y
34 - 2y = 3y + 4
<=>
x = 17 - y
5y = 30
<=>
y = 6
x = 17 - 6 = 11
Hope this helps!
:)
Please answer correctly !!!!!!! Will mark brainliest !!!!!!!!!!!

Answers
Answer:
100
Step-by-step explanation:
perfect square (a - b)^2 = a^2 - 2ab + b^2
In this case
20x = 2 * x * 10
and
10^2 = 100
so
(x - 10)^2 = x^2 - 20x + 100
Therefore, the missing constant term is 100
.
Sally is going to paint the 4 walls in her bedroom. Her bedroom is 3.5 m long , the breth is 2.8 m and 2.2 m high.
the door and window from her bedroom are together 3.2 m².
With one can of paint she can paint 4.5 m².
how much cans of paint does sally need?
Answers
I need help with this question too but less hope we get a answer
How do you write this number using digits?
five hundred six thousand eight hundred twenty-seven
Answers
Explanation: Google
consider the value of t such that the area to the left of −|t|−|t| plus the area to the right of |t||t| equals 0.010.01.
Answers
The value of t such that the area to the left of −|t| plus the area to the right of |t| equals 0.01 is: t = −|t1| + 0.005 = −0.245 (approx)
Let’s consider the value of t such that the area to the left of −|t|−|t| plus the area to the right of |t||t| equals 0.01. Now, we know that the area under the standard normal distribution curve between z = 0 and any positive value of z is 0.5. Also, the total area under the standard normal distribution curve is 1.Using this information, we can calculate the value of t such that the area to the left of −|t| is equal to the area to the right of |t|. Let’s call this value of t as t1.So, we have:
Area to the left of −|t1| = 0.5 (since |t1| is positive)
Area to the right of |t1| = 0.5 (since |t1| is positive)
Therefore, the total area between −|t1| and |t1| is 1. We need to find the value of t such that the total area between −|t| and |t| is 0.01. This means that the total area to the left of −|t| is 0.005 and the total area to the right of |t| is also 0.005.
Now, we can calculate the value of t as follows:
Area to the left of −|t1| = 0.5
Area to the left of −|t| = 0.005
Therefore, the area between −|t1| and −|t| is:
Area between −|t1| and −|t| = 0.5 − 0.005 = 0.495
Similarly, the area between |t1| and |t| is:
Area between |t1| and |t| = 1 − 0.495 − 0.005 = 0.5
Area to the right of |t1| = 0.5
Area to the right of |t| = 0.005
Therefore, the value of t such that the area to the left of −|t| plus the area to the right of |t| equals 0.01 is the value of t1 plus the value of t:
−|t1| + |t| = 0.005
2|t1| = 0.5
|t1| = 0.25
Therefore, the value of t such that the area to the left of −|t| plus the area to the right of |t| equals 0.01 is:
t = −|t1| + 0.005 = −0.245 (approx)
To know more on the normal distribution curve refer to:
https://brainly.com/question/30783928
#SPJ11
Graph a parabola whose vertex is at (3,5)(3,5)left parenthesis, 3, comma, 5, right parenthesis with yyy-intercept at y=1y=1y, equals, 1.
Answers
Using the given information we found that the equation of the parabola is:
y = (-4/9)*(x - 3)^2 + 5
And its graph is below.
How to get the equation of the parabola?
For a parabola with vertex (h, k), the equation is:
y = a*(x - h)^2 + k
Here the vertex is (3, 5), so the equation is:
y = a*(x - 3)^2 + 5
And the y-intercept is y = 1, this means that:
1 = a*(0 - 3)^2 + 5
1 = a*9 + 5
1 - 5 = a*9
-4/9 = a
So the parabola is:
y = (-4/9)*(x - 3)^2 + 5
And its graph is below.
If you want to learn more about parabolas, you can read:
https://brainly.com/question/1480401

Bridget correctly wrote a set of equivalent numbers. Which of the following sets of
numbers could have been what she wrote?
who ever answers first gets to be brainylest
Answers
Answer:
2/3, 66 2/3%, 0.666
Step-by-step explanation:
eqivalent
Answer:
The answer is 2/3, 66 2/3%, 0.6
Step-by-step explanation:
Because Im taking the DCA right now and i got that answer correct :3
which of the following expression is equivalent to the expression below 2(7x + 3)
1. 9x +3
2. 14x +6
3. 9x -6
4. 14x - 3
Answers
Answer:
14x+6
Step-by-step explanation:
Multiply 7x by 2 which gets you 14x and multiply 3 by 2 which is 6.
A cricket team scored 250 runs in their first innings. One player scored 30% of these runs. In the second innings, the same player scored 105 runs.Express his second innings score as a percentage of his first innings score.
Answers
Answer:
42%
Step-by-step explanation:
Hope it helps!
solve the given differential equation by undetermined coefficients. y''' y'' = 8x2 y(x) =
Answers
The given differential equation is y''' y'' = 8x².For solving the given differential equation by undetermined coefficients, we assume the solution to be in the form of y = ax² + bx + cHere, y''' y'' implies the highest power of x is 3.So, we need to consider the form of the particular solution to be in the form of Yp(x) = (Ax^3 + Bx^2 + Cx + D)x² + (Ex² + Fx + G)x + HWe differentiate the above equation as per the order of the differential equation.
Then, y'' = 6Ax + 2B, and y''' = 6ATherefore, the differential equation becomes6A * 2B = 8x²After solving for A and B, we get A = 4/9 and B = 0Now the equation becomesYp(x) = (4/9)x⁵ + E x³ + F x² + G x + HAlso, y'' = 2(4/9)x³ + 3Ex² + 2Fx + GAnd y''' = 8/3 x² + 6Ex + 2FSubstituting y,
y'', and y''' values in the original equation, we get:(8/3) x² + 6Ex + 2F * 2(4/9)x³ + 3Ex² + 2Fx + G= 8x²Comparing the coefficients of x³, x², x and the constants: (8/3)(4/9)x³ + 6E * 2F * 3Ex + 2G= 0On simplification, we get:(32/27) x³ + 18EFx + 2G = 0On comparing the coefficients of x³, x², x and the constants, we get:2G = 0G = 0So, the particular solution Yp(x) = (4/9)x⁵ + E x³ + F x² + HSince we have no information about the initial conditions, so the general solution is given by y(x) = C1 + C2 x + C3 x² + (4/9)x⁵ + E x³ + F x² + HTherefore, this is the required solution of the differential equation y''' y'' = 8x² by undetermined coefficients.
To know more about equation visit:
https://brainly.com/question/29538993
#SPJ11
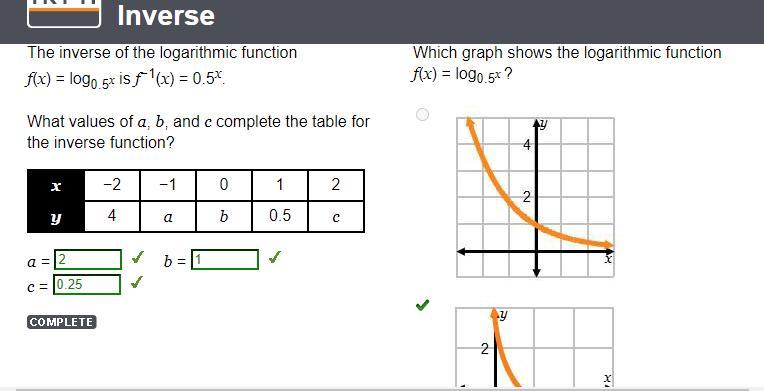
The inverse of the logarithmic function f(x) = log0.5x is f−1(x) = 0.5x. what values of a, b, and c complete the table for the inverse function? x −2 −1 0 1 2 y 4 a b 0.5 c a = b = c =
Answers
The value of a, b and c can be calculated using the inverse function.The calculated the value of a= 2, b=1 and c= 0.25
What is an inverse function?The inverse function of a function is defined if f is a function that undoes the operation \(f^{-1}\)
The inverse of f exists if and only if f is bijective, and if it exists, is denoted by \(f^{-1}\) .
It is given that the function \(\rm F(x)=Log_{0.5}x\) is and its inverse is
\(f^{-1}(x)=0.5^x\) .
Substitute the value of x= -1 in a given inverse function and calculate the value of a.
\(f^{-1}(x)=0.5^x\)
\(f^{-1}(-1)=0.5^{-1}\)
\(f^{-1}(-1)=2\)
Substitute the value of x is 0 in the given inverse function.
\(f^{-1}(x)=0.5^x\)
\(f^{-1}(0)=0.5^0\)
\(f^{-1}(0)=1\)
Substitute the value of x is 2 in the given inverse function.
\(f^{-1}(x)=0.5^x\)
\(f^{-1}(2)=0.5^2\)
\(f^{-1}(2)=0.25\)
Thus the value of a, b and c can be calculated using the inverse function.The calculated the value of a= 2, b=1 and c= 0.25
To know more about the Inverse function follow
https://brainly.com/question/20538141
Answer:
a = 2
b = 1
c = 0.25
Which graph shows the logarithmic function
f(x) = log0.5x ?
B.
Step-by-step explanation:
did it on ED :)
The interior angle measure of a regular polygon is calculated with the following formula, where n represents the number of sides or interior angles of the regular polygon.
Determine the measure of the interior angles of a regular octagon and identify whether or not a regular octagon can be used as the only shape in a regular tessellation.
144°, no
135°, yes
144°, yes
135°, no
THE RIGHT ANSWER IS A 144°, no
Answers
Answer:
Step-by-step explanation:
The interior angle measure of a regular polygon is calculated with 180*(n-2)/n, where n represents the number of sides.
A regular octagon has 10 sides so it interior angle = 180*(10-2)/10
= 144
A tessellation is a tile pattern with the same polygon repeating. The polygon's interior angles must combine to form 360 degree. A regular octagon has interior angle of 144 degree which does not add to 360 degree. So a regular octagon cannot be used as the only shape in a regular tessellation.
The answer is 144°, no.
Answer:
Step-by-step explanation:
oct means 10
(n-2)/n * 180
= (10-2)/10 * 180
= 144°
144 + 144 = 288 < 360
144 + 144 + 144 = 432 > 360
so a regular octagon can NOT be used as the only shape in a regular tessellation.
ans is A
what does 617 mean on red sox uniform
Answers
if f(x)= 3x -2, find f-1(x)
Answers
Answer: 1/3x + 2/3
Step-by-step explanation:
f(x)= 3x - 2 =>
y= 3x - 2 =>
x= 3y - 2 =>
3y - 2= x =>
3y= x + 2 =>
y= 1/3x + 2/3 =>
f-1(x)=1/3x + 2/3
How would you describe the difference between the graphs of f(x) = x^2 +4 and
g(y) - y^2 +4?

Answers
Answer:
Step-by-step explanation:
The function \(f(x)=x^2+4\) is a positive upwards opening parabola with the vertex at (0, 4), whereas
the function \(g(y)=y^2+4\) is a positive rightwards opening parabola (sideways parabola) with the vertex at (4, 0). This means that answer to this is that g(y) is reflected over the x axis whereas f(x) is reflected over the y axis.
That's driver pays all tall is using only nickels and dimes by throwing one coin at a time into the mechanical toll collector
Answers
Since nickel is 5 cents and a dime is 10 cents, the possible tolls that you can pay need to be multiplies of 5 cents.
Let on represent the number of a ways
for the number of different ways the bus
The driver can pay a toll of 5n rent first case.
The first case used in a nickel then there are ways to pay =
57 - 5 = 5 ( 1 - 1 ) cents
The second case: - The coin used is a dime, then
there is a long way to
pay 5n - 10 2 5 ( 1 - 2 ) cents -
Adding the numbers of sequence of all
In three cases, we then obtain
an = an - 1 an +2
Initially, when n 20 there is exactly I way to pay cents ( using no coins )
when an = 1 there is exactly I to way
to pay 5 cents ( using one tickle )
q =f .
Learn more about nickel here: https://brainly.com/question/9181464
#SPJ4
An item originally costs $175.00. The item is now on sale for $99.75. What percentis the sale price of the original price? Is this an example of percent increase ordecrease? Explain how you know.*
Answers
Let:
Op = Original price
Dp = Discount price
r = percent of discount
The discount price will be, the original price minus the product of the original price and the percent of discount, so:
\(\begin{gathered} Dp=Op-Op\cdot r \\ where \\ Op=175 \\ Dp=99.75 \\ 99.75=175-175\cdot r \\ 175\cdot r=175-99.75 \\ 175\cdot r=75.25 \\ r=\frac{75.25}{175} \\ r=0.43 \end{gathered}\)The percent of discount of the item is 43%
5.
Find the coordinates of B, C, and D given that AB = 5 and BC
= 10.
Answers
The coordinates of B, C, and D are (3,-5), (3,5), and (-7,5) respectively.
Given point A (-2,-5) and the lengths of the sides AB = 5 and BC = 10, we can use this information to determine the coordinates of B, C, and D.
Using the information provided, we know that B is 5 units away from A in the positive x-direction. Therefore, the x-coordinate of B is (-2) + 5 = 3 and the y-coordinate of B is the same as that of A, which is -5. So point B is (3,-5).
Next, we know that C is 10 units away from B in the positive y-direction. Therefore, the x-coordinate of C is the same as that of B, which is 3, and the y-coordinate of C is (-5) + 10 = 5. So point C is (3,5).
Finally, we know that D is 10 units away from C in the negative x-direction. Therefore, the x-coordinate of D is 3 - 10 = -7 and the y-coordinate of D is the same as that of C, which is 5. So point D is (-7,5).
To learn more about the coordinates at
https://brainly.com/question/16634867?referrer=searchResults
#SPJ4
The question is -
Find the coordinates of B, C, and D given that AB = 5 and BC = 10 where A = (-2,-5).
This is 2 parts of one of my practice problems. The current age used for the first question is 30 and the retirement age is 58. The amount wanted to save is $1,060,123.
a) You and your family would like to have a $X saving at the end of the year you retire. You are planning to retire at the age of Y. Given your age today (please specify an age, which doesn’t have to reflect your true age), and planning to make $400 monthly deposits, what rate should you earn annually to reach your retirement goal? (Hint: Use Rate function)
b) You would like to buy a car with a loan that charges APR of 3.69% per year compounded monthly, (3.69%/12 per month). You borrow $40,000 and promised to pay monthly in 5 years (5*12=60 months). What would be your monthly payments?
Thank you!
Answers
A retirement savings goal of $1,060,123 by the age of 58, while starting at the age of 30 and making monthly deposits of $400, an annual interest rate of 3.69% compounded monthly and agrees to make monthly payments over a period of 5 years.
a) To determine the required annual interest rate to reach the retirement savings goal, the Rate function can be used in financial calculations. The known values in this scenario are the starting age (30), the retirement age (58), the desired savings amount ($1,060,123), and the monthly deposits ($400). By using the Rate function, the interest rate required to achieve the goal can be calculated. The formula for the Rate function is Rate(Nper, PMT, PV, FV). In this case, Nper represents the number of periods (in years), PMT represents the monthly deposit amount, PV represents the present value (initial savings), and FV represents the future value (retirement savings goal). By plugging in the given values, the function can determine the required interest rate.
b) To calculate the monthly payments for a car loan, the known values are the borrowed amount ($40,000), the annual percentage rate (APR) of 3.69%, and the loan term of 5 years (or 60 months). The monthly interest rate is calculated by dividing the APR by 12 (to reflect monthly compounding). Using the loan formula for monthly payments, which is PMT = (P * r * (1 + r)^n) / ((1 + r)^n - 1), where PMT represents the monthly payment, P represents the principal amount (borrowed amount), r represents the monthly interest rate, and n represents the number of periods (in this case, the total number of months).
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Explain in 5-7 sentences what type of triangles can be used with the sine/cosine/tangent ratios.
Answers
The Solution.
The triangle that can be used with sine, cosine, and tangent ratios must have the following characteristics:
1. The triangle must be a right-angled triangle.
2. The triangle must have one of its angles as 90 degrees.
3. Another angle must be indicated as the angle of interest.
4. At least two sides and an angle must be identified/represented with values.
5. The ratios under consideration can be used to find all the angles and all the sides.
If a partical traveled a distance of 9.0×1012 meters at a rate of 1.8×105 meters per second. If distance = rate x time, how many seconds did it take the particle to travel the specified distance?
Answers
A particle traveled a distance of 9.0×10¹² meters in 5.0 × 10⁷ seconds.
What is division?The division in mathematics is one kind of operation. In this process, we split the expressions or numbers into the same number of parts.
Given:
If a particle traveled a distance of 9.0×10¹² meters at a rate of 1.8×10⁵meters per second.
And the distance,
= rate x time.
Rearranging the formula,
Time = Distance / rate
Time = 9.0×10¹² / 1.8×10⁵
Simplifying by using division operation,
Time = (9.0/1.8) × 10¹² × 10⁻⁵
Time = 5.0 × 10⁷
Therefore, the required specified time is 5.0 × 10⁷ seconds.
To learn more about the division;
https://brainly.com/question/13263114
#SPJ1
A customer has been following several investment company quotes in the newspaper. She notices that the GEM Fund has a net asset value (NAV) of $12 and a public offering price (POP) of $12.50, and that the ABC Fund has an NAV of $11.50 and a POP of $10.98. The customer should conclude that
Answers
The customer should conclude that the GEM Fund is being sold at a premium, as its POP is higher than its NAV. Conversely, the ABC Fund is being sold at a discount, as its POP is lower than its NAV.
The Net Asset Value (NAV) represents the value of a mutual fund's assets per share. It is calculated by dividing the total value of the fund's assets by the number of shares outstanding. The Public Offering Price (POP), on the other hand, is the price at which new shares of the mutual fund are being sold to investors.
In the given scenario, the GEM Fund has an NAV of $12 and a POP of $12.50. Since the POP is higher than the NAV, it indicates that investors are required to pay a premium of $0.50 per share to purchase the GEM Fund. This premium can be seen as an additional cost or fee associated with buying into the fund.
On the other hand, the ABC Fund has an NAV of $11.50 and a POP of $10.98. Here, the POP is lower than the NAV, suggesting that investors can purchase shares of the ABC Fund at a discount of $0.52 per share compared to its underlying asset value.
Therefore, based on the provided information, the customer can conclude that the GEM Fund is being sold at a premium, while the ABC Fund is being sold at a discount.
Learn more about Net Asset Value (NAV) here:
https://brainly.com/question/29988660
#SPJ11
Help me please..
Help me with the ones which are marked
8 points and brainliest

Answers
Answer:
1. 30
2. C = 18.3 B = 25% A=15 % rest = unkown
Step-by-step explanation:
to find X is what percent of Y
X/Y multiplied by 100
Please help me with this it's an emergency (a²=4+12)
Answers
Answer:
a=4,-4
Step-by-step explanation:
If three dice are rolled, what chance is there
of throwing a total of 18?
Answers
Answer:
1/216
Step-by-step explanation:
1/6 times 1/6 times 1/6
or 6^-3
Answer:
Step-by-step explanation:
There is only 1 way you can throw 18 with 3 dice. There are 6 * 6 * 6 = 216 ways of throwing 3 dice. Only 1 will give you 18. So the answer is 1/216
a) 5(3z-2)=-16-3(2z+5)
b) 5(2 –3k) + (3k –2) = -4
Answers
a) z=105.53
b) k= 1
What is the area of this parallelogram?

Answers
Answer:
88 m²
Step-by-step explanation:
Add the two bottom lengths to get
11 m
Multiply it with the height which is 8 m
11 m·8 m
88 m²
find the value of the expressions if n = 4.
1) 2n - 7
2) 3n² + 2n - 5
3) -m³
Answers
Step-by-step explanation:
Substitute n = 4 into the expression:
\(2(4)-7\)
Solve:
\(8-7\)
\(1\)
Substitute n = 4 into the expression:
\(3(4)^{2} +2(4)-5\)
Solve:
\(48+8-5\)
\(56-5\)
\(51\)
Substitute n = 4 into the expression:
Is the expression \(-n^{3} ?\)
\(-4^{3}\)
Multiply:
\(-4 \times -4 \times -4= -64\)