in a haplodiploid system, calculate the relatedness of a son to a maternal aunt.
Answers
In a haplodiploid system, the relatedness of a son to a maternal aunt is 75%.
In a haplodiploid system, males develop from unfertilized eggs and are haploid, while females develop from fertilized eggs and are diploid. This means that sons inherit all of their genetic material from their mother, including her alleles from both her haploid sets of chromosomes. Maternal aunts, on the other hand, share one set of haploid chromosomes with their nephew (the son), as they are the sister of his mother. Therefore, the relatedness between a son and his maternal aunt in a haplodiploid system is 0.75 or 75%.
In a haplodiploid system, the relatedness of a son to a maternal aunt can be calculated using the following steps:
1. Determine the relatedness of the son to his mother: In haplodiploid systems, sons are haploid and inherit their single set of chromosomes from their mother. This means that they are 100% related to their mother, as they share all her genes.
2. Determine the relatedness of the maternal aunt to the son's mother: The maternal aunt is a sister of the son's mother. In haplodiploid systems, sisters share 75% of their genes, as they get half of their genes from their mother and the other half from their father (who, as a haploid male, gives all his genes to his daughters).
3. Calculate the relatedness of the son to his maternal aunt: To determine the relatedness of the son to his maternal aunt, multiply the son's relatedness to his mother (100%) by the maternal aunt's relatedness to the son's mother (75%).
Relatedness of son to maternal aunt = (1.0) * (0.75) = 0.75 or 75%
So, in a haplodiploid system, the relatedness of a son to a maternal aunt is 75%.
Learn more about haplodiploid system here: brainly.com/question/31081669
#SPJ11
Related Questions
Write an equation for the line parallel to the given line that contains C.
5
C(1,7); y=x+4
Answers
The equation of the line parallel to the given line that contains C is obtained as y = x + 6.
What is termed as the parallel lines?Parallel lines are two or more lines which lie within the same plane but never intersect. They are equal in distance and have the same slope. Parallel lines have been straight lines which never meet, no matter how far they are extended. Numerous pairs of angles are formed when two parallel lines have been intersected by another line known as a transversal.For the given question;
The equation of the line is given as;
y = x + 4
The standard form of the equation of line in slope intercept form is;
y = m x + c
where, m is the slope and c is the y intercept.
On comparing;
m₁ = 1
Now, the other lien is parallel to the given line.
Thus, slopes of both lines will be equal.
m₁ = m₂ = 1
The passing points of the line are;
(x₁, y₁) = C(1, 7)
Now, the equation of lien will be;
y - y₁ = m₂(x - x₁)
Put the values;
y - 7 = 1(x - 1)
Simplifying.
y = x + 6
Thus, the equation of the line parallel to the given line that contains C is obtained as y = x + 6.
To know more about the parallel lines, here
https://brainly.com/question/12065995
#SPJ13
If a || b and ____, then a || c.
• b || c
• a upside down T c
• b upside down T c
• b upside down T a
Answers
Answer:
it will option A it is correct answer
5/3 x + 1/3 x = 40/3 + 8/3 x
Answers
Isolate the variable by dividing each side by factors that don't contain the variable.
x=−20
4 plus c as an algebraic expression
Answers
The required algebraic expression is c+4
What is an expression?An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation. This math operation can be addition, subtraction, multiplication, or division.
Given that a statement 4 plus c as an algebraic expression
We need to convert it into an expression,
4 = 4
plus = +
c = c
Therefore, arranging it = c+4
Hence, the required algebraic expression is c+4
Learn more about expressions, click;
https://brainly.com/question/14083225
#SPJ1
find the value of x
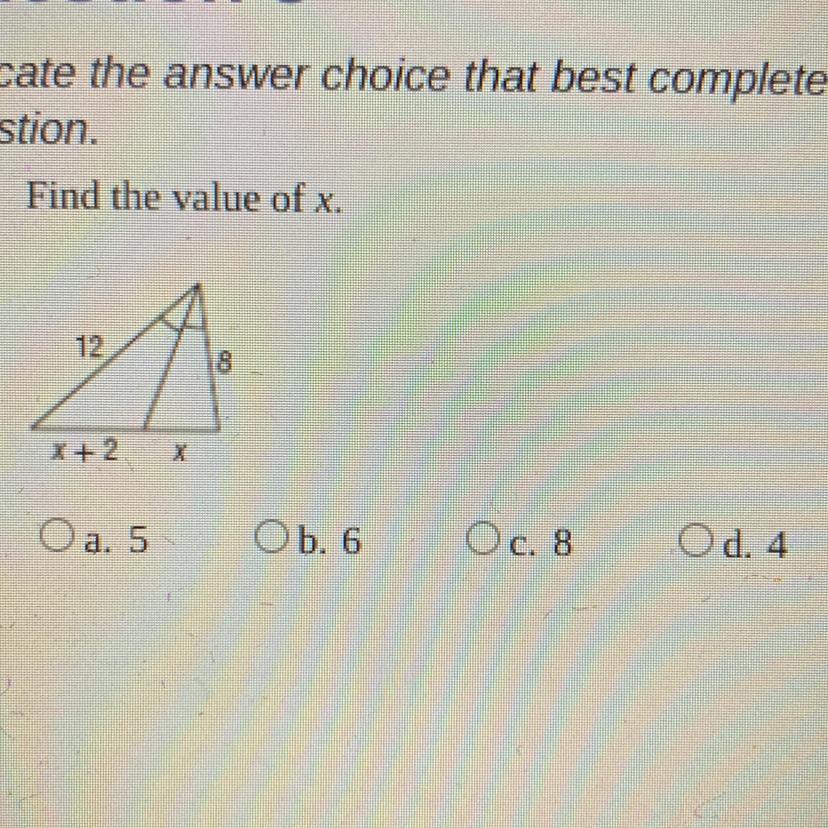
Answers
choose the correct answer to fill in the blank. an outlier is an observation which is less than iqr or greater than q3 ( )times iqr.
Answers
Outliers are any observations that fall more than 1.5 IQR below Q1 or more than 1.5 IQR above Q3.
Outliers:
While observing the data in the observations some of data may fall outside the general scope of the other observations. Such observations are called outliers.
Given,
An outlier is an observation which is less than IQR or greater than Q3 times IQR.
Here we need to find in Q1 and Q3 place variations.
When we use the IQR method of identifying outliers to set up a “fence” outside of Q1 and Q3. Any values which fall outside of the identified fence are considered outliers.
To build this fence we take 1.5 times the IQR and then subtract this value from Q1 and add this value to Q3.
Like,
IQR = (1.5 - Q1)
IQR = (1.5 + Q3)
This gives us the minimum and maximum fence posts that we compare each observation to.
Therefore, any observations that are more than 1.5 IQR below Q1 or more than 1.5 IQR above Q3 are considered outliers.
To know more about Outliers here.
https://brainly.com/question/26958242
#SPJ4
how to send kred to a krew member
Answers
To send Kred to a Krew member, you can follow the steps provided by the Kred platform. These steps typically involve accessing your Kred account, selecting the desired recipient, specifying the amount of Kred to send, and confirming the transaction.
Sending Kred to a Krew member usually requires using the features and functionalities provided by the specific Kred platform or service. The process may vary depending on the platform, so it is recommended to refer to the official documentation or guidelines provided by the platform. Typically, you would need to log in to your Kred account, navigate to the appropriate section for sending Kred, select the intended recipient from the list of Krew members, enter the desired amount of Kred to send, review the transaction details, and confirm the transfer. The platform may also offer additional options or settings for customizing the transfer process.
Learn more about Kred Platform here: brainly.com/question/29548334
#SPJ11
Unit 3 Parallel & Perpendicular Lines: Homework 3

Answers
Answer:
check the attached file
Step-by-step explanation:

a parametric inferential statistical test of the null hypothesis for a single sample where the population variance is known is the
Answers
The parametric inferential statistical test for a single sample with a known population variance is the one-sample z-test.The null hypothesis in this test is that the sample mean is equal to the population mean.
The one-sample z-test is a parametric test used to determine whether a sample mean is significantly different from a known population mean when the population variance is also known. This test assumes that the data are normally distributed and the sample is a random sample from the population.
The one-sample z-test is a statistical test used to test a hypothesis about a population mean when the population variance is known. It is a parametric test, which means that it makes assumptions about the population distribution and sample size. Specifically, it assumes that the data are normally distributed and that the sample is a random sample from the population. The test is called a z-test because it uses the standard normal distribution to calculate the test statistic. The test statistic is calculated by taking the difference between the sample mean and the population mean, and dividing it by the standard error of the mean. The standard error of the mean is calculated by dividing the population standard deviation by the square root of the sample size.
To know more than statistical visit :-
https://brainly.com/question/32201536
#SPJ11
a market researcher would like to know how much time the average college student spends watching sports. suppose he does a preliminary study based upon a sample of 25 college students. the mean amount of time spent watching sports, by those in the sample, is 90 minutes per day with a standard deviation of 15 minutes per day. a button hyperlink to the salt program that reads: use salt. (a) which of the following numbers gives the value of the point estimate? 15 25 90 95 (b) using the information given above, calculate the margin of error (in minutes) of the point estimate. assume we would like to estimate the population mean with 95% confidence. (use a table or technology. round your answer to two decimal places.) min (c) suppose that the researcher is not content with the current margin of error. he would like the margin of error of the point estimate to be no more than 4 minutes with 95% confidence. the researcher is unwilling to trust that the sample standard deviation from his previous study accurately estimates the true population standard deviation. he does, however, know that college students tend to watch sports between 0 and 120 minutes per day. what is the minimum sample size needed to obtain this amount of precision? (use a table or technology.) college students
Answers
The value of point estimate is 90. The margin of error of the point estimate is 5.9 minutes. The minimum sample size needed to obtain this amount of precision is 60.
(a) The point estimate is 90 as the sample mean amount of time spent watching sports by those in the sample is 90 minutes per day.
(b) Margin of error (ME) can be calculated asME = (z-score) × (standard deviation / √sample size)The formula for 95% confidence interval is z = 1.96, the standard deviation (SD) = 15, and sample size (n) = 25.ME = 1.96 × (15 / √25) = 5.88 ≈ 5.9 minutes
Therefore, the margin of error is 5.9 minutes.
(c) The maximum error of the point estimate that the researcher wants to allow is 4 minutes and the researcher knows that college students tend to watch sports between 0 and 120 minutes per day.
The formula for sample size (n) can be used to find the minimum sample size required to obtain this amount of precision.
n = (z-score / ME)² × p × (1 - p)where p = 0.5 (since we do not know the value of p).
z-score = 1.96 and ME = 4.n = (1.96 / 4)² × 0.5 × (1 - 0.5)n = 59.53 ≈ 60
Therefore, a minimum sample size of 60 college students is required to obtain the desired level of precision with 95% confidence.
Learn more about standard deviation (SD) here:
https://brainly.com/question/32027106
#SPJ11
You have exactly 10 coins with a total
value is $1. Three of the coins are
quarters. What are the remaining coins?
The
Answers
Answer:
2 dimes and 5 pennies
Step-by-step explanation:
2 dimes (d) is 10 and 5 pennies (p) is 5
75+p+d=100
75+p=80
80+d=100
Answer: 3 quarters, 2 dimes, 1 nickel.
Step-by-step explanation: 3 quarters are worth 75 cents, 2 dimes are worth 20 cents, and 1 nickel is worth 5 cents! Hope this helps
Discuss load vs deformation of wet-mix and dry-mix shotcrete with different reinforcement and discuss in a bullet point when each could be used.
Answers
Load vs deformation behavior of wet-mix and dry-mix shotcrete with different reinforcement can be summarized as follows:
Load vs Deformation Behavior of Wet-mix Shotcrete:
- Wet-mix shotcrete exhibits a gradual increase in load with deformation.
- The initial stiffness is relatively low, allowing for greater deformation before reaching its peak load.
- Wet-mix shotcrete tends to exhibit more ductile behavior, with a gradual post-peak load decline.
- The reinforcement in wet-mix shotcrete helps in controlling crack propagation and enhancing overall structural integrity.
Load vs Deformation Behavior of Dry-mix Shotcrete:
- Dry-mix shotcrete exhibits a relatively higher initial stiffness, resulting in less deformation before reaching the peak load.
- It typically shows a brittle behavior with a rapid drop in load after reaching the peak.
- The reinforcement in dry-mix shotcrete primarily helps in preventing the formation and propagation of cracks.
When to Use Wet-mix Shotcrete:
- Wet-mix shotcrete is commonly used in underground construction, such as tunnel linings and underground mines.
- It is suitable for applications where greater flexibility and ductility are required, such as seismic zones or areas with ground movement.
When to Use Dry-mix Shotcrete:
- Dry-mix shotcrete is often used in above-ground applications, such as architectural finishes, structural repairs, and protective coatings.
- It is preferred in situations where rapid strength development is required, as it typically achieves higher early strength than wet-mix shotcrete.
- Dry-mix shotcrete can be used in areas where a more rigid and less deformable material is desired, such as in structural elements subjected to high loads.
Therefore, wet-mix and dry-mix shotcrete exhibit different load vs deformation behavior due to their distinct mixing and application methods. Wet-mix shotcrete offers greater ductility and deformation capacity, making it suitable for applications with dynamic loading or ground movement.
On the other hand, dry-mix shotcrete provides higher early strength and is preferred for applications requiring rapid strength development or where rigidity is essential. The choice between wet-mix and dry-mix shotcrete depends on the specific project requirements, structural considerations, and the anticipated loading conditions.
Learn more about reinforcement visit:
https://brainly.com/question/30390489
#SPJ11
One angle of an isosceles triangle measures 40°. Which other angles could be in that
isosceles triangle? Choose all that apply.
40°
70°
100°
20°

Answers
Answer:
40 and 100
Step-by-step explanation:
If y varies directly with x when y=68 and x-6, find the value of y when x=24.
Answers
The value of y when x = 24 is 272.
What is proportionality?Proportionality indicates that two quantities or variables are related linearly.
Given that, y varies directly with x when y = 68 and x = 6
y/x = 68/6 = 34/3
Therefore, the proportion is 34/3
when x = 24
34/3 = y/24
y = 272
Hence, y = 272 when x = 24
For more references on Proportionality, click;
https://brainly.com/question/8598338
#SPJ1
Johanna will plant up to 32 acres on her farm with wheat and corn. Fewer than 11 acres will be planted with wheat
Answers
The answer is
w + c ≤ 32
w < 11
w - the number of acres of wheat
c - the number of acres of corn
Johanna will plant up to 32 acres on her farm with wheat and corn:
w + c ≤ 32
Fewer than 11 acres will be planted with wheat:
w < 11
The two inequalities are:
w + c ≤ 32
w < 11
Let p: A number is greater than 25.
Let q: A.number is less than 35.
If p ^ q is true, then what could the number be? Select two options.
Answers
Answer:
Here we do not have the options, so I will answer in a general way.
We have two statements:
p = A number is greater than 25
q = A number is less than 35
We want to have:
p ^ q is true
This means:
p and q are true.
So, we need to find a number such that both conditions are meet, so we need to find a number N such that
The number N is greater than 25 (from p)
The number N is less than 35 (from q)
So N can be any number between 25 and 35
So, some of the possible values of N are:
N = 26
N = 27
N = 28.6
N = 33
N = 34
Concluding, any number N ∈ (25, 35) can be a solution.
(Note that N = 25 and N = 35 are not solutions)
The equation y= mx+b is the equation of a line. Solve the equation for b.
Answers
Answer:
y-mx=b
Step-by-step explanation:
y is the combined result of mx + b, minusing mx from y will give you a remaining amount (that being b)
Solve lx + 2|=10
please
Answers
you get this answer by breaking the absolute value into positive and negative components
-8,-14,-20 whats the next term
Answers
because its counting by 6
Use the quadratic formula to solve for x.
2x² +7x+1=0
Answers
Answer:
Step-by-step explanation:
you can use the slide divide bottoms up method for this.
slide the 2 over to the 1 which gives:
x²+7x+2=0
then apply the quadratic formula to get
-7±√7²-4(1)(2)
______________
2
then we have
-7±√41÷2
( 4a - 5 ) + ( 3a + 6 )
Answers
17a - 5 + 6
17a + 1
Find the 12th term of the arithmetic sequence whose common difference is d=9 and whose first term is a1=4.
Answers
Answer:
103
Step-by-step explanation:
A12=a1+(12-1)d
A12=4+(11)9
A12=4+99
A12=103
Each side of a pentagon is 10 cm greater than the previous side. If the perimeter of this pentagon is 500 cm, find the lengths of the sides.
Answers
Answer:
(I'll leave cm out to save space and time in the answer)
the perimeter is 500, there are 5 sides. so on average a side will be 100.
that's already the important key idea.
it's indeed 100 for the third side, the second will be 10 less, the fourth 10 more (making the 2and and the 4th side 200 in sum, and therefore still 100 on average).
repeat this for the 1. and 5. side and we get:
80
90
100
110
120
On this problem, the answer has been worked out, but you must fill in the blanks in the solution.A recent study of 28 randomly selected employees of a company showed that the mean of the distance they traveled to work was 14.3 miles. The standard deviation of this sample was 2.0 miles. Find the 95% confidence interval for µ (the true mean time for all employees of the company). Round your answer to one place after the decimal point.

Answers
The 1st box: 14.3
second box: 2.052
Third box: 2
fourth box: 28
fifth box: 13.5
sixth box: 15.1
Explanation:\(\begin{gathered} nu\text{mber in survey = 28} \\ n\text{ = 28} \\ \text{degr}ee\text{ of fr}eedom\text{ = n - 1 = 28 - 1} \\ \text{degr}ee\text{ of freedom = }27 \end{gathered}\)\(\begin{gathered} \operatorname{mean}\text{ = }\bar{X}\text{ = 14.3} \\ \text{standard deviation = s = 2} \\ 1\text{ - }\alpha\text{ = 0.95} \end{gathered}\)\(\begin{gathered} To\text{ }find_{}t_{\frac{\alpha}{2}},\text{ }wewould\text{ use the degr}ee\text{ of fr}eedom,\text{ }\frac{\alpha}{2\text{ }}\text{ and t -table} \\ \text{from the table }t_{\frac{\alpha}{2}}\text{ = 2.052} \end{gathered}\)\(\begin{gathered} \bar{X}\text{ }\pm\text{ }t_{\frac{\alpha}{2}}(\frac{s}{\sqrt[]{n}})\text{ = }14.3\text{ }\pm\text{ 2.052(}\frac{2}{\sqrt[]{28}}) \\ \end{gathered}\)\(\begin{gathered} =14.3\text{ - 2.052(}\frac{2}{\sqrt[]{28}})<\text{ }\mu<\text{ }14.3\text{ +2.052(}\frac{2}{\sqrt[]{28}}) \\ =\text{ }14.3\text{ - 0.775 }<\text{ }\mu<\text{ 14.3 +0}.775 \\ =\text{ }14.3\text{ }\pm\text{ 0.775} \\ =\text{ }14.3\text{ }\pm\text{ 0.8} \end{gathered}\)\(\begin{gathered} So,\text{ the confidence interval is:} \\ \text{ 14.3 - 0.8 < }\mu\text{ <}14.3\text{ + 0.8} \\ 13.5\text{ < }\mu\text{ < }15.1 \end{gathered}\)
The 1st box: 14.3
second box: 2.052
Third box: 2
fourth box: 28
fifth box: 13.5
sixth box: 15.1
Weather data is collected to analyze wind speed according to temperature. Identify the variables as either input or output to label the table and graph.
Answers
Answer: column A= temperature column B= wind speed. Label A= wind speed label B= Temperature
Step-by-step explanation:
Answer:
Column A =
✔ temperature
Column B =
✔ wind speed
Label A =
✔ wind speed
Label B =
✔ temperature
Step-by-step explanation: Just did it in the assignment of edge :)
In a right angle triangle, the length of the opposite side of an angle is 3cm and the length of the hypotenuse is 5cm. The value of the angle is
Answers
Answer: 36.87 degrees.
Step-by-step explanation:
In a right-angle triangle, the length of the opposite side of an angle and the length of the hypotenuse can be used to find the value of the angle using the trigonometric ratios.
If we let the angle in question be denoted as "theta" and the length of the opposite side be "opp" and the length of the hypotenuse be "hyp", we can use the trigonometric ratio "sine" to find the value of the angle.
sin(theta) = opp/hyp
We are given that opp = 3 cm and hyp = 5 cm, so we can substitute these values into the equation:
sin(theta) = 3/5
We can now use an inverse trigonometric function, such as arcsin, to find the value of theta:
theta = arcsin(3/5)
The result of this calculation is theta = approximately 36.87 degrees. Therefore, the value of the angle is 36.87 degrees.
Answer:
30 mm
Step-by-step explanation:
3 x 10 mm ? hopefully its the right answer for you
Help me, please i need help or I'm gonna spend hours on this

Answers
Answer:
28 sq units
Step-by-step explanation:
to find the area of a triangle you multiply the base and height together and then divide by 2
in this problem, i counted and found the base = 7 units and
the height = 8 units
A = 7x8÷2
A = 56/2 = 28
can you guys help me please.

Answers
Answer:
question 1: answer is 4
question 2: answer is 1
Step-by-step explanation:
Solve the given initial-value problem. Give the largest interval I over which the solution is defined.
L di/dt +Ri =E, i(0)=i0 L, R, E, i0 constants
Answers
The solution to the given IVP is.\($i(t)-\frac{E}{R}+\left(i_0-\frac{E}{R}\right) e^{-\frac{R}{L}}$\)
Initial value problems describe a type of problem in calculus. Initial value problems in calculus concern differential equations with a known initial condition that specifies the value of the function at some point. The purpose of these problems is to find the function that describes the system, which can be done by integrating the differential equation.
Consider the initial value problem,
L \(\frac{d i}{d t}+R i=E \text {. }\)
The initial condition is. \($i(0)=i_0$\)
Rewrite the DE as,
\(\begin{gathered}L \frac{d i}{d t}+R i=E \\\frac{d i}{d t}+\frac{R}{L} i=\frac{E}{L}\end{gathered}$$\)
This is a linear DE.
Compare the DE \(\frac{d i}{d t}+\frac{R}{L} i=\frac{E}{L}$\) with the general DE \(\frac{d i}{d t}+P(t) i=Q(t)$\). Then \($P(t)=\frac{R}{L}$\) and \($Q(t)=\frac{E}{L}$\).
Find the integrating factor (IF).
\($$\begin{aligned}I F & =e^{\int P(t) \vec{t}} \\& =e^{\int\left(\frac{\pi}{\mathrm{I}}\right) \mathrm{A}} \\& =e^{\frac{\pi}{l^2}}\end{aligned}$$\)
Thus, the integrating factor is \($I F=e^{\frac{R^2}{2^2}}$\).
Now multiply both sides of the DE with the IF.
\($$\begin{array}{r}e^{\frac{R}{\bar{L}^t}}\left(\frac{d i}{d t}+\frac{R}{L} i\right)=\frac{E}{L} e^{\frac{R}{L^t}} \\\frac{d i}{d t} e^{\frac{\pi}{L^t}}+\frac{R}{L} e^{\frac{R}{\bar{L}^t}} i=\frac{E}{L} e^{\frac{\pi}{\bar{L}^t}} \\{\left[i e^{\frac{R}{L^2}}\right]=\frac{E}{L} e^{\frac{R^L}{L^t}}}\end{array}$$\)
Integrate on both sides.
\($$\begin{aligned}& \int\left[i e^{\frac{R}{L}}\right] d t=\int \frac{E}{L} e^{\frac{R}{L^t}} d t \\& i e^{\frac{R}{L^{\mathrm{r}}}}=\frac{E}{L} \int e^{\frac{\pi}{L^t}} d t \\& i e^{\frac{R}{\perp} r}=\frac{E}{L}\left[\frac{e^{\frac{R}{2}}}{\frac{R}{L}}\right]+C \\& i e^{\frac{R}{\Gamma}+}=\frac{E}{R} e^{\frac{R^2}{I^{+}}}+C \\& i(t)=\frac{\frac{E}{R} e^{\frac{R}{L^2}}+C}{e^{\frac{R}{D^2}}} \\& t(t)=\frac{E}{R}+C e^{-\frac{R}{L^t}} \\&\end{aligned}$$\)
Thus, the general solution to the \(\mathrm{DE}\) is \($i(t)=\frac{E}{R}+C e^{-\frac{R}{t^*}}$\).
Use the initial condition. \($i(0)=i_0$\)
Substitute \($t=0$\) and \($i(0)=i_0$\) in \($i(t)=\frac{E}{R}+C e^{-\frac{R}{I^t}}$\).
\($$\begin{aligned}& i(0)=\frac{E}{R}+C e^{-\frac{R}{I}(0)} \\& i_0=\frac{E}{R}+C e^0 \\& i_0=\frac{E}{R}+C \quad \text { use } e^0=1 \\& C=i_0-\frac{E}{R}\end{aligned}$$\)
Substitute \($C=i_0-\frac{E}{R}$\) in \($i(t)=\frac{E}{R}+C e^{-\frac{R}{L^1}}$\).
\($$\begin{aligned}& i(t)=\frac{E}{R}+C e^{-\frac{R}{I}} \\& i(t)=\frac{E}{R}+\left(i_0-\frac{E}{R}\right) e^{-\frac{\pi}{t^t}}\end{aligned}$$\)
Therefore, the solution to the given IVP is. \($i(t)-\frac{E}{R}+\left(i_0-\frac{E}{R}\right) e^{-\frac{R}{L}}$\).
For more such questions on Initial-value problems:
https://brainly.com/question/8736446
#SPJ4
Find the sum of the numbers between, and including, 551-600.
Sn=
Answers
The sum of the numbers between, and including, 551-600 is 28,775.
How to calculate the sum of the numbers between, and including, 551-600.Using the formula:
Sn = n/2 * (a1 + an)
where
Sn is the sum of the numbers,
n is the number of terms,
a1 is the first term, and
an is the last term.
From the question,
n = 50 (since there are 50 numbers between 551 and 600, inclusive),
a1 = 551, and
an = 600.
So we have:
Sn = 50/2 * (551 + 600)
= 25 * 1151
= 28,775
Therefore, the sum of the numbers between and including 551-600 is 28,775.
Learn more about arithmetic progression at:https://brainly.com/question/24191546
#SPJ1