In a certain country, the average age is 31 years old and the standard deviation is 4 years. If we select a simple random sample of 100 people from this country, what is the probability that the average?
Answers
The probability that the average age of a simple random sample of 100 people from the country is less than or equal to 32 years is approximately 0.9938 or 99.38%. This calculation is based on the central limit theorem and the population's average age of 31 years with a standard deviation of 4 years.
By applying the central limit theorem, we know that the distribution of sample means approaches a normal distribution as the sample size increases. In this case, the sample size is 100, which is considered sufficiently large.
To find the probability, we need to calculate the z-score corresponding to the desired average age of 32 years. The z-score formula is given by z = (x - μ) / (σ / √n), where x is the desired average age, μ is the population mean (31 years), σ is the population standard deviation (4 years), and n is the sample size (100).
Substituting the values into the formula, we have z = (32 - 31) / (4 / √100) = 1 / 0.4 = 2.5.
We can then consult the standard normal distribution table or use a calculator to find the probability associated with a z-score of 2.5. The probability is the area under the normal curve to the left of the z-score.
Based on the standard normal distribution table, the probability is approximately 0.9938. Therefore, there is a 99.38% probability that the average age of the simple random sample of 100 people will be less than or equal to 32 years.
To learn more about Standard deviation, visit:
https://brainly.com/question/475676
#SPJ11
Related Questions
19. A quadratic equation is shown below.
a2-b=0
If b is a perfect square, which represents the solutions to the equation?
HELP PLEASE
Answers
Answer:
\(\{\sqrt b, -\sqrt b\}\)
Step-by-step explanation:
Given
\(a^2 - b = 0\)
Required
Determine the solution
Since b is a perfect square, the equation can be expressed as:
\(a^2 - (\sqrt b)^2 = 0\)
Apply difference of two squares:
\((a - \sqrt b)(a + \sqrt b) = 0\)
Split:
\((a - \sqrt b)= 0 \ or\ (a + \sqrt b) = 0\)
Remove brackets:
\(a - \sqrt b= 0 \ or\ a + \sqrt b = 0\)
Make a the subject in both equations
\(a =\sqrt b \ or\ a =-\sqrt b\)
The solution can be represented as:
\(\{\sqrt b, -\sqrt b\}\)
Suki says the area of the triangle is 12 cm². Emilia says the area of the triangle is 10 cm². Find the area of the triangle and explain any errors the girls might have made.
helpppp
Answers
Answer:
Let’s call the base of the triangle b and its height h. The area of a triangle is given by the formula A = 1/2 * b * h.
If Suki says that the area of the triangle is 12 cm², then we can write:
12 = 1/2 * b * h
Similarly, if Emilia says that the area of the triangle is 10 cm², then we can write:
10 = 1/2 * b * h
We can solve for one of the variables in terms of the other by dividing both sides of each equation by 1/2:
b * h = 24
b * h = 20
Now we have two equations with two variables. We can solve for one variable in terms of the other by dividing both sides of one equation by the other:
(b * h) / (b * h) = 24 / 20
1 = 6/5
This is a contradiction, so there is no solution that satisfies both equations.
Step-by-step explanation:
Find XZ given the mid-segment?

Answers
Answer:
16
having a hunch ig
9.
Find the values of x and y.
to
35 degrees
(i need
work shown please)
end answers should b x: 145
y: 35

Answers
Step-by-step explanation:
y is a corresponding angle to the 35 degree angle so y = 35°
'x' + the 35 degree angle form a straight line = 180 degrees
x + 35 = 180
x = 145°
Format your answer as needed
The perimeter is 36.what dose x have to be
Answers
Convert the equation from Standard to General form
Can somebody help me ASAP

Answers
Answer:x squred+ y squared +4y-21=25
Step-by-step explanation:
can yu help me pls "simplify45x^15
9x^10"

Answers
Answer:
The answer is 5x^5
Step-by-step explanation:
45/9 is equaled to 5
The number that are powered 15 and 10 would be subtracted
10-5=5
5x^5
Hope this helps please mark brainliest :)
Which of the following is a characteristic of Euclidean geometry?
A. No lines are straight.
B. The sum of the measures of the angles in a triangle is greater than 180 degrees.
C. The parallel postulate is true.
D. The sum of the measures of the angles in a triangle is less than 180 degrees.
Answers
Answer:
b
Step-by-step explanation:
bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
help me with this !!

Answers
Multiply the probability of getting a correct answer (0.25) with the number of questions (68) to get 0.25*68 = 17
The student should expect to get about 17 questions correct.
M is the midpoint of RT. RM = 5x + 9 and MT = 8x - 36. Find x, RM, MT, and RT. = .
Answers

The values of x, RM, RT, and MT are 15, 84, 168, and 84 respectively.
What is a System of equations?simultaneous equations, a system of equations Two or more equations in algebra must be solved jointly (i.e., the solution must satisfy all the equations in the system). The number of equations must match the number of unknowns for a system to have a singular solution.
There are four methods for solving systems of equations: graphing, substitution, elimination, and matrices.
Given a system of equations Where RM = 5x + 9 and MT = 8x - 36.
Since,
M is the midpoint of RT
Thus,
RM = MT
5x + 9 = 8x - 36
3x = 45
x = 15
So,
1) RM = 5x + 9
RM = 75 + 9 = 84
2) MT = 8x -36
MT = 120 - 36 = 84
3) RT = RM + MT
RT = 84 +84 = 168
Therefore, The values of x, RM, RT, and MT are 15, 84, 168, and 84 respectively.
Learn more about the System of equations here:
https://brainly.com/question/12628931
#SPJ5
Albert is a marine biologist studying the bluefin tuna population in Caro Bay. When he first started monitoring the population, there were about 1,550 bluefin tuna in the bay. One year later, he estimated that the population of bluefin tuna had decreased to about 1,488. Albert expects the population of bluefin tuna to continue decreasing each year.
Write an exponential equation in the form y=a(b)x that can model the population of bluefin tuna in Caro Bay, y, x years after Albert began monitoring it.
Use whole numbers, decimals, or simplified fractions for the values of a and b.
Answers
The exponential function that models the population of bluefin tuna after x years is given as follows:
y = 1550(0.96)^x.
The parameters of the exponential function are given as follows:
a = 1550.b = 0.96.How to define the exponential function?An exponential function is defined as follows:
y = a(b)^x.
For which the parameters are given as follows:
a is the initial value.b is the rate of change.When he first started monitoring the population, there were about 1,550 bluefin tuna in the bay, meaning that the parameter a is given as follows:
a = 1550.
One year later, he estimated that the population of bluefin tuna had decreased to about 1,488, hence the parameter b is obtained as follows:
b = 1488/1550 = 0.96.
Hence the function is defined as follows:
y = 1550(0.96)^x.
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
Distribute to create an equivalent expression with the fewest symbols possible.
4(x - 2 + y) =
Answers
Answer:
4x-8+4y
Step-by-step explanation:
Answer:
4x - 8 + 4y
Step-by-step explanation:
4 (x - 2 + y)
= 4x - 8 + 4y
Of all the closed right circular cylindrical cans of volume 128πcm
3, find the dimensions of the can which has minimum surface area.
Answers
The can's minimum surface area should have a height of 8 cm and a radius of 4 cm.
Given:
The volume of closed right circular cylindrical cans = 128π cm³
As we know the volume of a cylinder = πr²h
By equating;
πr²h = 128π
h = 128/r²
To get the dimensions of a can with minimum surface area;
S = 2πrh + 2πr
Put h = 128/r²;
Therefore, S(r) = 256π/r + 2πr²
S'(r) = -256π/r² + 4πr
S''(r) = -(2*256π)/r³ + 4π
Now, for S(r) = 0;
r = 4cm
for S''(4) > 0 at r = 4 is minimum point.
Hence,
h = 128π/(π*4*4)
h = 8cm
Therefore, the minimum surface area of the can should have a radius of 4 cm and a height of 8 cm.
To learn more about right circular cylinder click here:
brainly.com/question/28448651
#SPJ4
What are all the zeros of the function f(x) = 4x^2 + 8x + 3?

Answers
Answer: -1/2 and -3/2
Step-by-step explanation:
I think I’m not sure
Consider the two triangles shown below. Two triangles. The first triangle has a side length of five units, a one hundred seventeen degree angle, a side of seven units. The second triangle has a side length of five units, a one hundred seventeen degree angle, a side of seven units. Two triangles. The first triangle has a side length of five units, a one hundred seventeen degree angle, a side of seven units. The second triangle has a side length of five units, a one hundred seventeen degree angle, a side of seven units. Note: The triangles are not drawn to scale. Are the two triangles congruent
Answers
In this case, both triangles have a side length of 5 units and a side length of 7 units, and they share an angle of 117 degrees. Therefore, they satisfy the ASA criterion, and we can conclude that they are congruent.
Congruent?Congruent is a mathematical term used to describe two figures or shapes that have the same size and shape. In other words, two figures are congruent if they have exactly the same dimensions and the same angles. When two figures are congruent, they can be superimposed on each other without any overlap or gap between them. Congruent figures are often denoted by the symbol ≅. For example, if two triangles have the same size and shape, we can write them as ∆ABC ≅ ∆DEF, which means that triangle ABC is congruent to triangle DEF. Congruent figures play an important role in geometry and other branches of mathematics.
Yes, the two triangles are congruent.
In Euclidean geometry, if two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles are congruent. This is known as the angle-side-angle (ASA) congruence criterion.
In this case, both triangles have a side length of 5 units and a side length of 7 units, and they share an angle of 117 degrees. Therefore, they satisfy the ASA criterion, and we can conclude that they are congruent.
To know more about angle-side-angle visit:
https://brainly.com/question/29124246
#SPJ1
By using the Cauchy's Residue Theorem, show that 4-3z cz³ -3z²+2z C dz = 2πi.
Answers
By applying Cauchy's Residue Theorem to the given integral, we can show that the integral equals 2πi. This theorem allows us to evaluate the integral by summing the residues of the singular points enclosed by the contour.
The Cauchy's Residue Theorem states that if f(z) is analytic inside and on a simple closed contour C, except for finitely many isolated singular points, then the integral of f(z) over C is equal to 2πi times the sum of the residues at those singular points.
In the given integral, we have the function f(z) = 4 - 3z cz³ - 3z² + 2z and the contour C. To evaluate the integral using the residue theorem, we need to identify the singular points enclosed by the contour. In this case, we can see that the function f(z) has a pole of order 3 at z = 0.
To find the residue at z = 0, we can use the formula for the residue of a pole of order n:
Res(f, 0) = 1 / (n-1)! * lim(z→0) [d^(n-1)/dz^(n-1) (z^n f(z))]
In this case, n = 3, so we have:
Res(f, 0) = 1 / 2! * lim(z→0) [d²/dz² (z³ f(z))]
Evaluating the derivative, we obtain:
Res(f, 0) = 1 / 2! * lim(z→0) [d²/dz² (z³ (4 - 3z cz³ - 3z² + 2z))]
Simplifying further, we find:
Res(f, 0) = 1 / 2! * lim(z→0) [d²/dz² (4z³ - 3z^5 c - 3z^4 + 2z^4)]
Res(f, 0) = 1 / 2! * lim(z→0) [d²/dz² (4z³ - 3z^5 c - z^4)]
Taking the second derivative, we get:
Res(f, 0) = 1 / 2! * lim(z→0) [d/dz (12z² - 15z^4 c - 4z³)]
Res(f, 0) = 1 / 2! * (24z - 60z³ c - 12z²) evaluated at z = 0
Res(f, 0) = 1 / 2! * (0 - 0 - 0)
Res(f, 0) = 0
Since the residue at z = 0 is 0, the integral of f(z) over the contour C equals 2πi times the sum of the residues, which is 2πi * 0 = 0. Therefore, the given integral is equal to 0.
To learn more about function click here: brainly.com/question/9554035
#SPJ11
how could you represent 0.614 using only 5 tenths
Answers
We can represent 0.614 using only 5 tenths as \(\mathbf{\dfrac{6.14}{10}}\)
What is a decimal number?A decimal is a number that is divided into two parts: a whole and a fraction. Between integers, decimal numbers are used to express the numerical value of complete and partially whole quantities.
The accepted method for representing both integer and non-integer numbers is the decimal number system.
From the given information, we are to represent 0.614 by using only 5 tenths.
5 tenths can be mathematically expressed as:\(\mathbf{=\dfrac{5}{10}}\)Representing 0.614 in the same form, we have:
\(\mathbf{=\dfrac{0.614\times 1000}{1\times 1000}}\)
\(\mathbf{=\dfrac{614}{1000}}\)
\(\mathbf{=\dfrac{6.14}{10}}\)
Learn more about representing decimals in the fractional form here:
https://brainly.com/question/2877484
#SPJ 10
Answer: 6.14/10
Step-by-step explanation:
Answer the question and find the code.

Answers
The slope of the line passing through the points (3, 4) and (5, 8) is 2.
We have,
To find the slope of a line passing through two points (x₁, y₁) and (x₂, y₂), you can use the formula:
slope = (y₂ - y₁) / (x₂ - x₁)
In this case,
The points are (3, 4) and (5, 8).
Let's substitute these values into the formula:
slope = (8 - 4) / (5 - 3)
= 4 / 2
= 2
Therefore,
The slope of the line passing through the points (3, 4) and (5, 8) is 2.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ1
You are trying to decide how much to save for retirement. Assume you plan to save $4,500 per year with the first investment made one year from now. You think you can earn 5.5% per year on your investments and you plan to retire in 35 years, immediately after making your last $4,500 investment. a. How much will you have in your retirement account on the day you retire? b. If, instead of investing $4,500 per year, you wanted to make one lump-sum investment today for your retirement that will result in the same retirement saving, how much would that lump sum need to be? c. If you hope to live for 17 years in retirement, how much can you withdraw every year in retirement (starting one year after rement will just exhaust your savings with the 17th withdrawal (assume your savings will continue to earn 5.5% in retirement)? d. If, instead, you decide to withdraw $90,000 per year in retirement (again with the first withdrawal one year after retiring), how many years will it take until you exhaust your savings? (Use trial-and-error, a financial calculator: solve for "N", or Excel: function NPER) e. Assuming the most you can afford to save is $900 per year, but you want to retire with $1,000,000 in your investment account, how high of a return do you need to earn on your investments? (Use trial-and-error, a financial calculator: solve for the interest rate, or Excel: function RATE)
Answers
This retirement planning scenario involves saving a fixed amount per year, earning a specified interest rate, and determining the final retirement account balance, lump-sum investment amount, annual withdrawal in retirement, and required interest rate for a specific savings goal. The details are as follows:
a. retirement account balance of approximately $536,144.37
b. The lump sum required would be approximately $60,319.79.
c. With an account balance of $536,144.37, the annual withdrawal would be approximately $46,914.90.
d. It would take approximately 16 years until the savings are depleted.
e. Through trial and error, it can be determined that an interest rate of approximately 10.47% is needed to achieve the desired savings goal.
a. The retirement account balance on the day of retirement can be calculated by using the formula for the future value of an ordinary annuity. In this case, saving $4,500 per year for 35 years with an annual interest rate of 5.5% will result in a retirement account balance of approximately $536,144.37.
b. To achieve the same retirement savings goal with a lump-sum investment today, the present value of an ordinary annuity formula can be used. The lump sum required would be approximately $60,319.79.
c. Assuming a retirement duration of 17 years and a desire to exhaust the savings with the 17th withdrawal, the annual withdrawal can be calculated using the formula for the annuity payment. With an account balance of $536,144.37, the annual withdrawal would be approximately $46,914.90.
d. If the decision is made to withdraw $90,000 per year in retirement, the number of years until the savings are exhausted can be determined using the formula for the number of periods in an annuity. It would take approximately 16 years until the savings are depleted.
e. If the maximum affordable annual saving is $900 and the goal is to retire with $1,000,000, the required interest rate can be calculated using the formula for the rate of return. Through trial and error, it can be determined that an interest rate of approximately 10.47% is needed to achieve the desired savings goal.
These calculations provide insights into the financial aspects of retirement planning and can help individuals make informed decisions about their savings, investments, and withdrawal strategies based on their specific goals and constraints.
Learn more about rate of return here:
https://brainly.com/question/30761579
#SPJ11
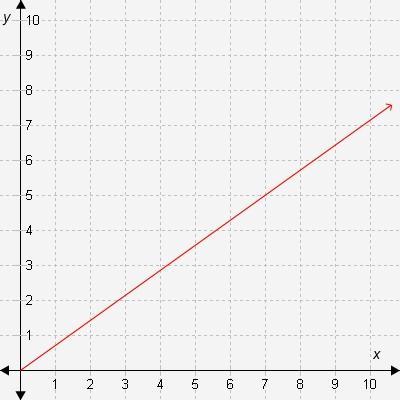
Please help! Correct answer only! What is the slope of the line in this graph?
A. 5/9
B. 5/7
C. 7/5
D. 9/7
Answers
Answer:
B. 5/7
Step-by-step explanation:
Up the y axis by 5 and over the x axis by 7
The point-slope equation of a line is....? HELP ME
Answers
(in survey done in a group of 500 children, 250 children liked doughnut only and 30% liked bread but not doughnut. If every children likes at least one of them.): (i)Find the number of children who liked both doughnut and bread. (ii)Find the number of children who like bread
Answers
Step-by-step explanation:
Come over here
fja-fsbf-knf
What’s the answer for number 8? Show work and explain

Answers
Answer:
so simple do it yourself and use the formula when is given in the text book to solve
Inga is solving 2x2 + 12x – 3 = 0. Which steps could she use to solve the quadratic equation? Select three options.
Answers
Steps (A) 2(x² + 6x + 9) = 3 + 18 and (B) 2(x² + 6x) = 3 can be used to solve the given quadratic equation.
What are quadratic equations?An algebraic equation of the second degree in x is a quadratic equation.
The quadratic equation is written as ax² + bx + c = 0, where x is the variable, a and b are the coefficients, and c is the constant term.
So, let's examine the first option:
2(x² + 6x + 9) = 3 + 18
We'll now multiply 2 by each component of the other multiplier on the left:
2·x² + 2·6x + 2·9 = 3 + 18
2x² + 12x + 18 = 3 + 18
2x² + 12x - 3 = 18 - 18
2x² + 12x - 3 = 0
Let's examine the second option:
2(x² + 6x) = 3
We'll now multiply 2 by each component of the other multiplier on the left:
2·x² + 2·6x = 3
2x² + 12x = 3
2x² + 12x - 3 = 0
Therefore, steps (A) 2(x² + 6x + 9) = 3 + 18 and (B) 2(x² + 6x) = 3 can be used to solve the given quadratic equation.
Know more about quadratic equations here:
https://brainly.com/question/1214333
#SPJ1
Correct question:
Inga is solving 2x2 + 12x – 3 = 0. Which steps could she use to solve the quadratic equation? Check all that apply.
A. 2(x2 + 6x + 9) = 3 + 18
B. 2(x2 + 6x) = –3
C. 2(x2 + 6x) = 3
x + 3 =
D. 2(x2 + 6x + 9) = –3 + 9
(x + 3)2 =
How to interpret data regarding marginal effects on probit model?
Marginal Effects:
dF/dx Std. Err. z P>|z|
firstDdiff 0.00302663 0.00712841 0.4246 0.671138
PassYdif 0.00258074 0.00050826 5.0776 3.822e-07 ***
RushYdif 0.00468025 0.00060833 7.6936 1.431e-14 ***
`Away Dummy` -0.17577822 0.06001699 -2.9288 0.003403 **
`TO Diff` 0.26602856 0.02582057 10.3030 < 2.2e-16 ***
---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
dF/dx is for discrete change for the following variables:
[1] "`Away Dummy`"
> probitmfx(probit, data = X2018NFLSeasonWinsOnFieldStats, atmean = FALSE)
Call:
probitmfx(formula = probit, data = X2018NFLSeasonWinsOnFieldStats,
atmean = FALSE)
Marginal Effects:
dF/dx Std. Err. z P>|z|
firstDdiff 0.00144898 0.00341176 0.4247 0.671054
PassYdif 0.00123551 0.00022395 5.5168 3.452e-08 ***
RushYdif 0.00224064 0.00023421 9.5666 < 2.2e-16 ***
`Away Dummy` -0.08706381 0.03032556 -2.8710 0.004092 **
`TO Diff` 0.12735916 0.00756113 16.8439 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Answers
The given data presents the marginal effects estimated from a probit model. Each row represents a variable, and the corresponding values show the marginal effect, standard error, z-statistic, and p-value. The marginal effect, represented as dF/dx, measures the change in the probability of the dependent variable (usually a binary outcome) resulting from a one-unit change in the independent variable.
In a probit model, the marginal effects provide insights into how changes in the independent variables affect the probability of the dependent variable. The estimated marginal effects indicate the direction and significance of these effects.
For example, a positive marginal effect indicates that an increase in the corresponding independent variable leads to a higher probability of the outcome occurring. Conversely, a negative marginal effect suggests a decrease in the probability. The standard error quantifies the uncertainty associated with the marginal effect estimate, and the z-statistic and p-value assess the statistical significance of the effect.
The significance codes provided (***, **, *, etc.) indicate the level of significance at which the null hypothesis (no effect) can be rejected. Lower p-values suggest higher significance. Researchers can use these results to understand the relative importance of different variables in influencing the probability of the outcome.
It's important to note that interpreting marginal effects requires considering the context of the model, the specific variables involved, and any assumptions made during estimation.
Learn more about probit model here:
https://brainly.com/question/29608754
#SPJ11
. Let Sn n! for all n E N. Prove that Sn →→→ 0 as n nn → [infinity].
Answers
We can conclude that \(\(S_n \to 0\)\) as \(\(n \to \infty\)\) since for any positive value \(\(M\),\) we can find an index \(\(N\)\) such that for all \(\(n \geq N\), \(S_n\)\) is less than \(\(M\).\)
How to Prove that Sn →→→ 0 as n nn → [infinity]To prove that \(\(S_n \to 0\)\) as \(\(n \to \infty\),\) where \(\(S_n = n!\)\) for all \(\(n \in \mathbb{N}\),\) we can use the concept of the factorial function.
We know that \(\(n! = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1\).\)
As \(\(n\)\) increases, the value of \(\(n!\)\) grows exponentially. However, it is not enough to show that \(\(n!\)\) grows without bound to prove that \(\(S_n\)\) tends to infinity. We need to show that the growth of \(\(S_n\)\) is greater than any arbitrary positive value.
Let's consider an arbitrary positive value \(\(M > 0\)\). We want to find an index \(\(N\)\) such that for all \(\(n \geq N\), \(S_n\)\) is less than\(\(M\).\)
Since \(\(S_n = n!\)\), we have:
\(\(S_n = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1\).\)
For any\(\(n \geq 2\)\), we can write:
\(\(S_n = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1 \geq n \cdot (n-1) \cdot (n-2) \cdot 2 \geq 2^{n-1}\).\)
Now, we can choose an index \(\(N\)\) such that \(\(2^{N-1} > M\)\). This is possible since \(\(2^{N-1}\)\) can be made arbitrarily large by increasing (N).
Therefore, for all \(\(n \geq N\)\), we have:
\(\(S_n \geq 2^{n-1} > M\).\)
This shows that for any arbitrary positive value \(\(M\)\), there exists an index \(\(N\)\) such that for all \(\(n \geq N\)\), \(\(S_n\)\) is greater than \(\(M\).\)
Hence, we can conclude that \(\(S_n \to 0\)\) as \(\(n \to \infty\)\) since for any positive value \(\(M\),\) we can find an index \(\(N\)\) such that for all \(\(n \geq N\), \(S_n\)\) is less than \(\(M\).\)
Learn more about function at https://brainly.com/question/11624077
#SPJ4
a stained glass window is in the shape of a sqare. a sketch of the window, with some of its dimensions is shown below =. what is the length to the nearets 10 of a foot of the line segment labeled x?
Answers
The length to the nearest 10th of a foot of the line segment labeled x is approximately 2.8 feet.
In order to determine the length of the line segment labeled x, we need to first understand the relationship between the sides of a square.
Since all sides of a square are equal in length, we can use the Pythagorean theorem to find the length of x.
The Pythagorean theorem states that for any right triangle, the sum of the squares of the lengths of the two legs (the sides that form the right angle) is equal to the square of the length of the hypotenuse (the side opposite the right angle).
In this case, we can consider x as the hypotenuse of a right triangle with legs of length 2 feet.
Using the Pythagorean theorem, we can write:
\(x^2 = 2^2 + 2^2\)
\(x^2\) = 4 + 4
\(x^2\) = 8
Taking the square root of both sides, we find:
x = sqrt(8)
Simplifying this expression, we get:
x = 2*sqrt(2)
To find the length of x to the nearest 10th of a foot, we need to convert this value to decimal form and round to the nearest 10th.
Using a calculator, we find:
x = 2.82842712475
Rounding this to the nearest 10th, we get:
x ≈ 2.8 feet
For more related questions on line segment:
https://brainly.com/question/30072605
#SPJ11
Can someone help me plz???

Answers
Answer:
7n - 13
Step-by-step explanation:
First you have to distribute it so it becomes: 4n + 3n + (-15) + 2.
Then, you combine the like terms.
Simplify (x-5)+(X+1)
Answers
Answer:
2x - 4
Step-by-step explanation:
x - 5 + x + 1
→Add like terms (x and x, -5 and 1):
2x - 4
A rocket is launched in to the air with an initial upward velocity of 375 ft/s, from ground
level. Which of the following equations best models this scenario?
Answers
Answer:
h(t)=-16t^2+375t
Step-by-step explanation: