If XY=YZ=95, WX=u+66, and WZ=7u, what is XZ?
Answers
The value of XZ is approximately equal to 96.86.
What is inequality ?
An inequality is a mathematical statement that compares two values, expressions, or quantities using inequality symbols such as "<" (less than), ">" (greater than), "<=" (less than or equal to), ">=" (greater than or equal to), or "≠" (not equal to).
We can start by using the transitive property of equality to find that XY = YZ = 95 means that XY + YZ = XZ = 190.
Next, we can use the given information about WX and WZ to write an equation for XZ in terms of u. Since WZ = WX + XZ, we can substitute the given expressions to get:
7u = (u + 66) + XZ
Simplifying and solving for XZ, we have:
7u - u - 66 = XZ
6u - 66 = XZ
Now, we can substitute this expression for XZ into our earlier equation to get:
XZ = 190 = 95 + 95 = XY + YZ = (WX - 66) + (6u - 66)
Simplifying and solving for u, we get:
6u - 66 = 190 - WX
6u = 256 - WX
u = (256 - WX)/6
Substituting this value of u back into the expression for XZ, we get:
XZ = 6u - 66 = 6[(256 - WX)/6] - 66 = 190 - WX
Therefore, XZ = 190 - WX, where WX = u + 66 = (256 - WX)/6 + 66. We can solve for WX by multiplying both sides by 6:
6WX = 256 - WX + 396
7WX = 652
WX = 93.14 (rounded to two decimal places)
Substituting this value into our expression for XZ, we have:
XZ = 190 - WX = 190 - 93.14 = 96.86 (rounded to two decimal places)
Therefore, XZ is approximately equal to 96.86.
To learn more about Inequality from given link.
https://brainly.com/question/30228778
#SPJ1
Related Questions
The perimeter of a rectangle is 96 yards and the length is 14 yards more than the width what are the dimensions of the rectangle
Answers
Answer:
17 yards and 31 yards.
Step-by-step explanation:
Since length is 14 more than width, lets call width: w and length: w+14
So perimeter is 96 so: 2w+2(w+14)=96
2w+2w+28=96 so 4w+28=96
4w=68 and finally w=17
So 17 yards and 31 yards.
foreach function do the signs of the first and second deritives of the function appear to be positve or negative over te given interval?
X 1 1.1 1.2 1.3 1.4 1.5
F(x) 7.1 6.1 5.0 3.8 2.5 1.1
a) F’(X) appears to be
Answers
When using the `foreach` function, the signs of the first and second derivatives of the function appear to be negative over the given interval. What is the `foreach` function?The `foreach` function in PHP is utilized for iterating over arrays or objects. The `foreach` function works by stepping through each value of an array, and one iteration can be done for each of the array's elements, which can include key-value pairs. It is mainly utilized to execute a block of code for each element of an array.What is a derivative?A derivative is a calculus concept that refers to the slope of a function at a certain point. It is usually the rate at which a function's value changes as its input variable changes. Derivatives are widely utilized in many fields, including physics, engineering, and economics.How to determine the signs of the first and second derivative?We can determine the signs of the first and second derivative by finding the derivative of the given function f(x). Once we find the derivative of the function, we can put the values in a table like the following:X 1 1.1 1.2 1.3 1.4 1.5f(x) 7.1 6.1 5.0 3.8 2.5 1.1 We can calculate the first derivative of f(x) by the following formula:f'(x) = f(x + 1) - f(x)We can calculate the second derivative of f(x) by the following formula:f"(x) = f'(x + 1) - f'(x)Based on the table above, we can determine that the signs of the first and second derivatives of the function are negative over the given interval.
#SPJ11
The signs of the first derivative of the function F(x) over the given interval are not consistent, so it is difficult to determine whether it appears to be positive or negative.
The first derivative of a function represents the rate of change of the function at a given point, while the second derivative represents the curvature or concavity of the function at that point.
To determine the signs of the first derivative of F(x) over the given interval, we need to find the slope of the tangent line at each point. We can do this by calculating the difference between consecutive y-values and dividing by the corresponding difference in x-values.
For example, the slope between (1, 7.1) and (1.1, 6.1) is (6.1 - 7.1)/(1.1 - 1) = -1, which indicates a negative slope. However, the slope between (1.2, 5.0) and (1.3, 3.8) is (3.8 - 5.0)/(1.3 - 1.2) = -12, which indicates a much steeper negative slope.
We can repeat this process for each pair of consecutive points to find the sign of the first derivative at each point. However, since the signs of the slopes are not consistent over the given interval, we cannot determine whether the first derivative appears to be positive or negative.
In other words, the function may be increasing or decreasing at different rates over different portions of the interval, which makes it difficult to make a general statement about the sign of the first derivative.
To learn more about derivative here:
brainly.com/question/29020856#
#SPJ11
if :ℝ2→ℝ2 is a linear transformation such that ([10])=[7−3], ([01])=[30], then the standard matrix of is
Answers
Given that,ℝ2 → ℝ2 is a linear transformation such that ([1 0])=[7 −3], ([0 1])=[3 0].
To find the standard matrix of the linear transformation, let's first understand the standard matrix concept: Standard matrix:
A matrix that is used to transform the initial matrix or vector into a new matrix or vector after a linear transformation is called a standard matrix.
The number of columns in the standard matrix depends on the number of columns in the initial matrix, and the number of rows depends on the number of rows in the new matrix.
So, the standard matrix of the linear transformation is given by: [7 −3][3 0]
Hence, the required standard matrix of the linear transformation is[7 −3][3 0].
#SPJ11
Learn more about linear transformation and standard matrix https://brainly.com/question/20366660
11. Which of the following lines is perpendicular to the line 3x-9y = 17?
A) 12x + y = 4
B) 9x - 3y = 11
C) 6x + 2y = 8
D) 3x - y = 5
Answers
Step-by-step explanation:
When using the equation of a line, one calculates the value of
y
in terms of
x
, say
y
=
m
x
+
c
, then
m
is the slope of the line and
c
is its intercept on
y
-axis.
As
3
x
−
9
y
=
15
can be written as
3
x
−
15
=
9
y
or
y
=
3
9
x
−
15
9
or
y
=
1
3
x
−
5
3
Hence slope of
3
x
−
9
y
=
15
is
1
3
Product of slopes of two perpendicular lines is
−
1
Hence, the slope of the line that is perpendicular to the line
3
x
−
9
y
=
15
is
−
1
1
3
=
−
1
×
3
1
=
−
3
graph{(3x-9y-15)(3x+y+5)=0 [-10, 10, -7.04, 2.96]}
From 150 minutes to 172 minutes
Answers
3. A particle starts moving from the point (2,1,0) with velocity given by v(t) = (2t, 2t - 1,2 - 4t), where t > 0. (a) (3 points) Find the particle's position at any time t. (b) (4 points) What is the cosine of the angle between the particle's velocity and acceleration vectors when the particle is at the point (6,3,-4)? (c) (3 points) At what time(s) does the particle reach its minimum speed?
Answers
a) The position function is x(t) = t^2 + 2, y(t) = t^2 - t + 1, z(t) = 2t - 2t^2
b) Tthe cosine of the angle between the velocity and acceleration vectors at the point (6, 3, -4) is: cosθ = (v(6) · a(6)) / (|v(6)| |a(6)|) = 134 / (sqrt(749) * sqrt(24))
c) The particle reaches its minimum speed at t = 1/12.
(a) To find the particle's position at any time t, we need to integrate the velocity function with respect to time. The position function can be obtained by integrating each component of the velocity vector.
Given velocity function: v(t) = (2t, 2t - 1, 2 - 4t)
Integrating the x-component:
x(t) = ∫(2t) dt = t^2 + C1
Integrating the y-component:
y(t) = ∫(2t - 1) dt = t^2 - t + C2
Integrating the z-component:
z(t) = ∫(2 - 4t) dt = 2t - 2t^2 + C3
where C1, C2, and C3 are constants of integration.
Now, to determine the specific values of the constants, we can use the initial position given as (2, 1, 0) when t = 0.
x(0) = 0^2 + C1 = 2 --> C1 = 2
y(0) = 0^2 - 0 + C2 = 1 --> C2 = 1
z(0) = 2(0) - 2(0)^2 + C3 = 0 --> C3 = 0
Therefore, the position function is:
x(t) = t^2 + 2
y(t) = t^2 - t + 1
z(t) = 2t - 2t^2
(b) To find the cosine of the angle between the velocity and acceleration vectors, we need to find both vectors at the given point (6, 3, -4) and then calculate their dot product.
Given velocity function: v(t) = (2t, 2t - 1, 2 - 4t)
Given acceleration function: a(t) = (d/dt) v(t) = (2, 2, -4)
At the point (6, 3, -4), let's find the velocity and acceleration vectors.
Velocity vector at t = 6:
v(6) = (2(6), 2(6) - 1, 2 - 4(6)) = (12, 11, -22)
Acceleration vector at t = 6:
a(6) = (2, 2, -4)
Now, let's calculate the dot product of the velocity and acceleration vectors:
v(6) · a(6) = (12)(2) + (11)(2) + (-22)(-4) = 24 + 22 + 88 = 134
The magnitude of the velocity vector at t = 6 is:
|v(6)| = sqrt((12)^2 + (11)^2 + (-22)^2) = sqrt(144 + 121 + 484) = sqrt(749)
The magnitude of the acceleration vector at t = 6 is:
|a(6)| = sqrt((2)^2 + (2)^2 + (-4)^2) = sqrt(4 + 4 + 16) = sqrt(24)
Therefore, the cosine of the angle between the velocity and acceleration vectors at the point (6, 3, -4) is:
cosθ = (v(6) · a(6)) / (|v(6)| |a(6)|) = 134 / (sqrt(749) * sqrt(24))
(c) To find the time(s) when the particle reaches its minimum speed, we need to determine when the magnitude of the velocity vector is at its minimum.
Given velocity function: v(t) = (2t, 2t - 1, 2 - 4t)
The magnitude of the velocity vector is:
|v(t)| = sqrt((2t)^2 + (2t - 1)^2 + (2 - 4t)^2) = sqrt(4t^2 + 4t^2 - 4t + 1 + 4 - 16t + 16t^2)
= sqrt(24t^2 - 4t + 5)
To find the minimum speed, we can take the derivative of |v(t)| with respect to t and set it equal to 0, then solve for t.
d|v(t)| / dt = 0
(1/2) * (24t^2 - 4t + 5)^(-1/2) * (48t - 4) = 0
Simplifying:
48t - 4 = 0
48t = 4
t = 1/12
Therefore, the particle reaches its minimum speed at t = 1/12.
To know more about calculating velocity refer to this link-
https://brainly.com/question/30559316#
#SPJ11
How do the expressions 9+m2−3 and 8(m+3)−2m compare when m = 8?
Drag a symbol into the box to correctly complete the statement.
9+m2−3 Response area 8(m+3)−2m when m = 8.
<
=
>
Answers
Answer:
<
Step-by-step explanation:
I took the test. Please mark brainliest
Which of the below is/are true? Suppose A is an m X n matrix and x is in R". A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights. For the product Ax to be defined, the number of rows of A must be equal to the number of entries inx. c A linear combination ca; + ... + c,,a, can be written as a product of a matrix A = [a, an] by the vector (41,...,.). D. The product Ax is a vector in R". E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from rowi of A and the vectorx. The operation of a matrix-vector multiplication is linear since A(u + v) = Au + Av and Acu) = c(Au) hold for all vectors u and vin R" and all scalars c. PHIM
Answers
The true statements from the options provided are:
A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights.
D. The product Ax is a vector in \(R^n\).
E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from row i of A and the vector x.
What is linear combination?A linear combination in mathematics is an expression created from a group of terms by multiplying each component by a constant and combining the results (for example, an expression of the form axe + by, where a and b are constants, would be a linear combination of x and y).
The true statements from the options provided are:
A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights.
D. The product Ax is a vector in \(R^n\).
E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from row i of A and the vector x.
These statements accurately describe properties and definitions related to matrix-vector multiplication. The product Ax is obtained by taking a linear combination of the columns of A, where the entries of x act as weights. The resulting product Ax is a vector in \(R^n\), and its entries are calculated by summing the products of the corresponding entries from row i of A and the vector x.
Learn more about linear combination on:
https://brainly.com/question/30364543
#SPJ4
△DEF∼△XYZ Solve for x.
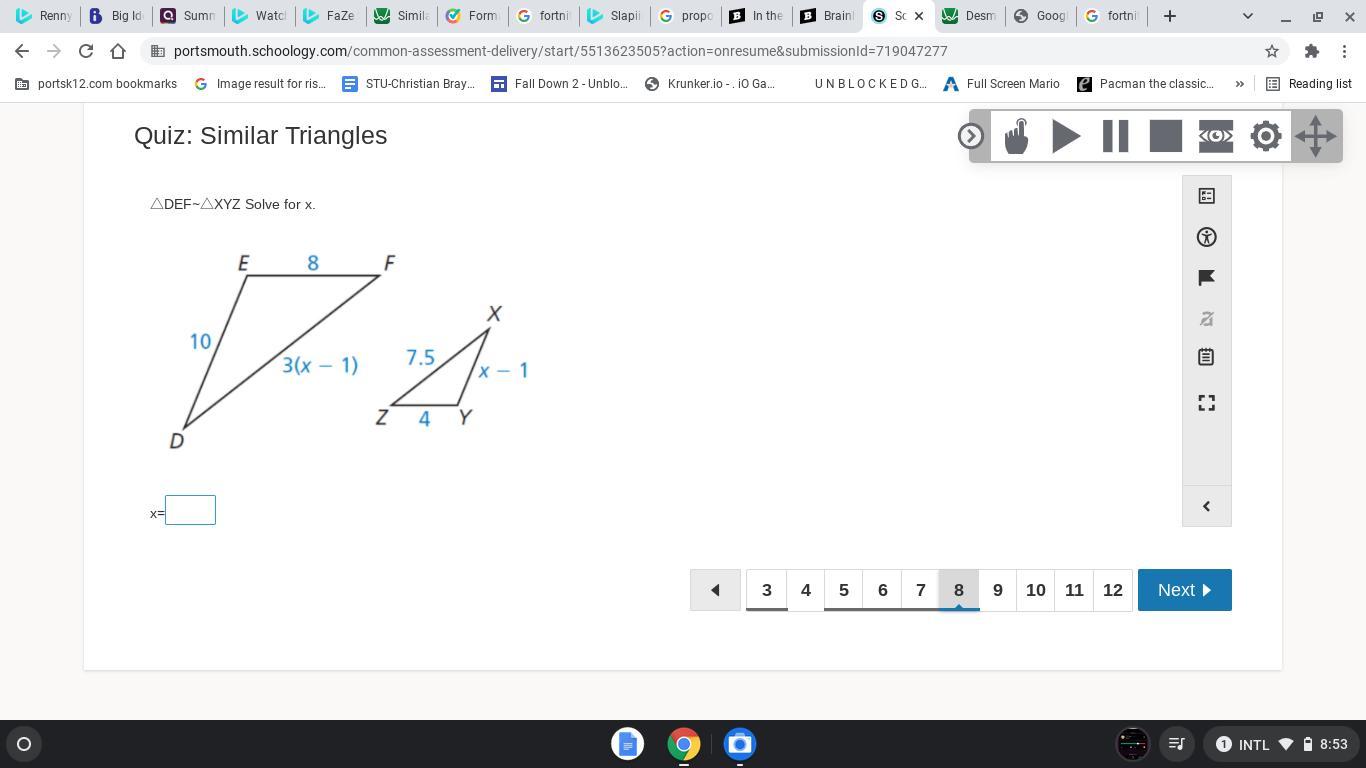
Answers
Answer:
x = 6
Step-by-step explanation:
Since the triangles are similar then the ratios of corresponding sides are in proportion, that is
\(\frac{DE}{XY}\) = \(\frac{EF}{YZ}\) , substitute values
\(\frac{10}{x-1}\) = \(\frac{8}{4}\) = 2 ( multiply both sides by x - 1 )
2(x - 1) = 10 ( divide both sides by 2 )
x - 1 = 5 ( add 1 to both sides )
x = 6
A first number is 4 less than a second number. Four times the first number is 6 more than twice the second. Find the numbers
Answers
Answer:
first number = 7
second number = 11
Step-by-step explanation:
A first number is 4 less than a second number
f = s - 4
Four times the first number is 6 more than twice the second
4f = 2s + 6
-----------------------------
Substitute for f = s - 4
4(s - 4) = 2s + 6
distribute
4s - 16 = 2s + 6
subtract 2s from both sides
2s - 16 = 6
add 16 to both sides
2s = 22
Divide both sides by 2
s = 11
Substitute for s = 11 in
f = s - 4
f = 11 - 4
f = 7
Please help me on this question

Answers
Answer:
C) 84 mm squared
Step-by-step explanation:
The formula for finding area of a triangle is 1/2 times base times height, so substitute and solve for the answer
1/2 times 8 times 21
4 times 21
84
Help me with my math please, it’s 6th grade

Answers
Itd be the 2nd answer from the top.
What can you see in this form of the linear equation? 6x+2y=13
Answers
The given equation 6x+2y=13 is a linear equation in two variables. In this equation, x and y are variables while 6 and 2 are their respective coefficients, and 13 is a constant term. The equation can be represented as a straight line on a graph. The slope of this line is -3, and it intersects the y-axis at the point (0, 13/2).
In this equation, if we substitute x=0, then y=13/2, and if we substitute y=0, then x=13/6. These are the two points that the line passes through the x and y-axis.
A linear equation is a polynomial equation that is of the first degree, meaning the variables in the equation are not raised to any powers other than one. This equation is in the standard form where the variables are in the first degree. 6x + 2y = 13 is the form of the given linear equation. x and y are the two variables, and 6 and 2 are their respective coefficients. The equation can be represented as a straight line on a graph. The slope-intercept form of this equation is y = -3x + 13/2. The equation is also in standard form.
When x = 0, the equation becomes 2y = 13. This means that the point of intersection is (0, 13/2) when y = 0, the equation becomes 6x = 13, and the point of intersection is (13/6, 0). The slope of the line is -3. When x increases by 1, y decreases by 3.
To know more about linear equation refer here:
https://brainly.com/question/29111179
#SPJ11
Y = (x - 3)^2
What is the product of y if if x=9
Answers
Hey there!
y = (x - 3)^2
y = (9 - 3)^2
y = (6)^2
y = 6 * 6
y = 36
Therefore, your answer is: y = 36
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
if the distance to a star was suddenly cut in half, how many times brighter would the star appear?
Answers
If the distance to a star was suddenly cut in half, it would appear four times brighter.
The brightness of a star is directly proportional to the inverse square of its distance from us. This means that if the distance to a star is halved, its brightness will increase by a factor of four.
The relationship between brightness and distance can be expressed as follows:
B = k / d^2
where B is the brightness, k is a constant of proportionality, and d is the distance.
If the distance to the star is halved, it can be expressed as:
d' = d / 2
Plugging this into the equation for brightness, we get:
B' = k / (d / 2)^2
Expanding this and simplifying, we get:
B' = 4 * k / d^2
Since k is a constant, it cancels out and we are left with:
B' = 4 * B
This means that if the distance to a star was suddenly cut in half, it would appear four times brighter. In astronomical terms, this is equivalent to an increase of 2 magnitudes on the logarithmic magnitude scale.
To know more about star distance click here:
https://brainly.com/question/2293327#
#SPJ11
−1.64 as a mixed number in simplest form.
Answers
-41\25
In a run chart, the variable being measured is typically placed on what axis?
(A) X axis
(B) Y axis
(C) Either axis
(D) Neither axis;
Answers
Find the specified value for the arithmetic sequence with the given characteristics. & 16 =
52, d = -2 a1 =?
Answers
Answer:
i actually dont know the answer i just need
Step-by-step explanation:
points lol sorry shawty
circle $c$ has radius 10 cm. how many square centimeters are in the area of the largest possible inscribed triangle having one side as a diameter of circle $c$?
Answers
100 square centimeters are in the area of the largest possible inscribed triangle having one side as a diameter of circle.
What is the area?
A two-dimensional figure's area is the amount of space it takes up. In other terms, it is the amount that counts the number of unit squares that span a closed figure's surface. In general, square units such as square inches, square feet, etc. are used as the standard unit of area.
Base = 2r = 2*10 = 20 cm
Height = r= 10 cm
Area = 1/2 * base * height
= 1/2 * 20 * 10
= 100 square centimeters
To learn more about the area from the given link
https://brainly.com/question/25292087
#SPJ4
Quadrilateral QUAD is circumscribed about a circle. If QU 19, UA 12, and AD what is the measure of QD? 15,
Answers
The measure of QD in quadrilateral QUAD is 22
How to find the measure of QD in quadrilateral?To find the measure of QD in quadrilateral QUAD, which is circumscribed about a circle, we can use the properties of a circumscribed quadrilateral.
Step 1: Recall that in a circumscribed quadrilateral, opposite sides sum up to the same value. That is, QU + AD = UA + QD.
Step 2: Substitute the given values: QU = 19, UA = 12, and AD = 15. So, 19 + 15 = 12 + QD.
Step 3: Simplify and solve for QD: 34 = 12 + QD.
Step 4: Subtract 12 from both sides: QD = 34 - 12.
Step 5: Calculate QD: QD = 22.
The measure of QD in quadrilateral QUAD is 22.
Learn more about quadrilateral
brainly.com/question/29934440
#SPJ11
please help fast i need it

Answers
Answer:
37/10
Step-by-step explanation:
\( \frac{3.7}{1} \\ \frac{37}{10} \)
37 is prime, therefore it has no factors to simplify the fraction.
A triangle has two sides of lengths 6 and 9. What value could the length of
the third side be? Check all that apply.
OA. 7
B. 2
C. 4
OD. 15
□E. 10
O F. 12
SUBMIT
Answers
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
To determine the possible values for the length of the third side of a triangle, we need to consider the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given that two sides have lengths 6 and 9, we can analyze the possibilities:
6 + 9 > x
x > 15 - The sum of the two known sides is greater than any possible third side.
6 + x > 9
x > 3 - The length of the unknown side must be greater than the difference between the two known sides.
9 + x > 6
x > -3 - Since the length of a side cannot be negative, this inequality is always satisfied.
Based on the analysis, the possible values for the length of the third side are:
A. 7
C. 4
□E. 10
O F. 12
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
for such more question on lengths
https://brainly.com/question/24176380
#SPJ8
Here you go. 29-28+28+11-11=?
Answers
Answer:
29
Step-by-step explanation:
Answer:
29
Step-by-step explanation:
29-28=1
1+28=29
29+11=40
40-11=29
Thank you for this challenge that was half the challenge of a challenge........
Better hope you stay up long enough to see the animatronics. :)
please help me with this please i will give brainlist if it's right!!

Answers
Answer:
1: 22
2: 4.9 and 6
Step-by-step explanation:
Question 1:
Step 1: Remove the outlier (the outlier is a data point that's significantly different from the other data points.)
\(21, 23, 19, 25, 83, 23, 21\) \(21, 23, 19, 25, 23, 21\)Step 2: Find the mean (add all the data points together and then divide them by the number of data points there is.)
\(\frac{21+23+19+25+23+21}{6}\) \(\frac{132}{6}\) \(22\)Therefore, the answer to question #1 is 22.
Question 2:
1. (Calculate the mean)
\(\frac{4+6+7+9+10+4+6+5+4}{9}\) \(\frac{55}{9}\) \(6.111...\) ≈ \(\frac{55}{9}\)2. Find the values less than \(\frac{55}{9}\).
8.1 > 55/9 (not less than)4.9 < 55/9 (less than)6 < 55/9 (less than)6.2 > 55/9 (not less than)7 > 55/9 (not less than)Therefore, the answer to question #2 is 4.9 and 6.
Plz help me I don’t want to fail

Answers
Edward works at a clothing store, and works on commission.
The amount he makes each week depends on how much clothing he sells, and he also receive a weekly amount regardless of his sales. Edward also had to pay for his meals during his shifts, which retracts from his income.
Edward's income can be modelled by the following equation:
I= 100+12J+5T+7S+5H-8M
where I is his income, J is the number of jeans he sells, T is the number of T-shirts he sells, S is the number of shorts he sells, H is the number of hats he sells and M is the number of meals he buys.
If Edward makes $197 in a week and sells:
5 pairs of jeans, 5 T-shirts, and 3 hats,
and buys 3 of his meals.
How many pairs of shorts did he sell?
Answers
Edward cannot have a fraction of a pair of shorts, we can conclude that Edward sold approximately 0.286 pairs of shorts.
To find out how many pairs of shorts Edward sold, we can substitute the given values into the equation and solve for S.
Given:
I = $197
J = 5
T = 5
H = 3
M = 3
Substituting these values into the equation:
$197 = 100 + 12(5) + 5(5) + 7S + 5(3) - 8(3)
Simplifying the equation:
$197 = 100 + 60 + 25 + 7S + 15 - 24
$197 = 195 + 7S
To isolate S, we subtract 195 from both sides:
$197 - $195 = 7S
$2 = 7S
Now, we divide both sides
176+ 7S
S ≈ 0.286
Since we cannot have a fraction of a pair of shorts, we can conclude that Edward sold approximately 0.286 pairs of shorts.
For such more questions on Shorts sold
https://brainly.com/question/27672621
#SPJ11
{[8-3)×2]+[(5×6)-5]}÷5
Answers
Answer:
35
Step-by-step explanation:
Using the table above. If your values are the following, what is your final grade ?

Answers
Question:
Solution:
According to the weighted average, and the grade that the person obtained, the grade of each item would be:
TEST AVERAGE:
85 x 0.50 = 42.5
FINAL TEST GRADE:
90 x 0.20 = 18
HOMEWORK
95 x 0.15 = 14.25
CLASS PARTICIPATION
80 x 0.15 = 12
Thus, the total grade is:
42.5 + 18 + 14.25 + 12 = 86.75
that is the total grade would be
86.75 out of a total of 100 points as the maximum grade

find the difference (20m+3)-(7m-5)
Answers
Answer:
13m + 8
Step-by-step explanation:
Distribute
(20m + 3) - 1(7m - 5)
(20m + 3) - 7m + 5
Eliminate redundant parentheses
(20m + 3) - 7m + 5
20m + 3 - 7m + 5
Add the Numbers
20m + 3 - 7m + 5
20m + 8 - 7m
Combine Like Terms
20m + 8 - 7m
13m + 8
Solution
13m + 8
The difference of the given equation i.e. (20m+3)-(7m-5) should be considered as the 13m + 8.
Calculation of the difference:Since the equation is (20m+3)-(7m-5)
So,
= 20m + 3 - 7m + 5
= 13m + 8
Hence, The difference of the given equation i.e. (20m+3)-(7m-5) should be considered as the 13m + 8.
Learn more about an difference here: https://brainly.com/question/13793217?referrer=searchResults
Need help
Having a hard time with this question
and gets 70 points for this

Answers
Step-by-step explanation:
According to the Alternate Exterior Angles Theorem, when a transversal cuts two parallel lines, the alternate exterior angles are congruent.
In this scenario, angle ZCXP is an alternate exterior angle with respect to angles ZRYD and ZSYD. Since angle ZRYD is congruent to angle ZSYD, angle ZCXP is also congruent to angle ZRYD.
Therefore, the correct answer is A. ZRYD.