If another teacher with an age of 45 is added to the data, how would the mean be impacted?
The mean would decrease in value to about 41.
The value of the mean would remain the same at about 44.
The value of the mean would remain the same at about 46.
The mean would increase in value to about 47.
Answers
Answer:
As we do not have any information about the ages of the existing teachers in the data set, we cannot determine the exact impact of adding a teacher with an age of 45 on the mean.
However, we can make some general observations. If the age of the new teacher (45 years) is less than the mean age of the original data set, then the addition of the new teacher would decrease the mean age. Conversely, if the age of the new teacher is greater than the mean age of the original data set, then the addition of the new teacher would increase the mean age.
Related Questions
6 - 2 4/7 = ?
answer asap and correct pls.
Answers
Answer:
24/7
Step-by-step explanation:
1) The area of a rectangle is 72 square feet. If the length is 14 feet more
than the width, find the length and the width.
Answers
Answer:
Length = 18 ft
Width = 4 ft
Step-by-step explanation:
Let the width of the rectangle be x ft
Therefore, length = (x + 14) ft
Area of rectangle = 72 sq ft
\( \therefore \: x(x + 14) = 72 \\ \therefore \: {x}^{2} + 14x - 72 = 0 \\\therefore \: {x}^{2} + 18x - 4x - 72 = 0 \\\therefore \: x(x + 18) - 4(x + 18) = 0 \\ \therefore \:(x + 18)(x - 4) = 0 \\ \therefore \:x + 18 = 0 \: \: or \: \: x - 4 = 0 \\ \therefore \:x = - 18 \: or \: \: x = 4 \\ \because \: dimensions \: of \: a \: rectangle \: \\ cn \: not \: be \: negative \\ \therefore \: x \neq \: - 18 \\ \implies \: x = 4 \\ \therefore \: x + 14 = 4 + 18 = 18 \\ length \: of \:the \: rectangle \: = 18 \: ft \\ width \: of \: the \: rectangle = 4 \: ft\)
which statements are true about the reflectional symmetry of a regular heptagon? select two options.
Answers
There are seven lines of symmetry in a heptagon. In a heptagon, the sides and angles are equal. Each vertex and the center of a regular heptagon are where the line of symmetry crosses.
What is Reflectional Symmetry ?
Any symmetry with regard to a reflection is referred to as reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry. In other words, a figure with reflectional symmetry does not alter when it is reflected. There is a line/axis of symmetry in 2D and a plane of symmetry in 3D. When a form or pattern is mirrored in a line of symmetry or a mirror line, this is known as reflective symmetry. The reflected form will have the same size, distance from the mirror line, and other characteristics as the original shape. When a figure can be split into two equal halves that match, it has line symmetry or reflection symmetry.
If a figure can be reflected over a line and retain its original appearance, it possesses reflection symmetry. If a figure can be altered while maintaining its appearance, it possesses symmetry.
To learn more about Reflective symmetry refer to :
brainly.com/question/30357862
#SPJ4
Complete question
Which statements are true about the reflectional symmetry of a regular heptagon? Check all that apply. It has only 1 line of reflectional symmetry. A line of symmetry will connect 2 vertices. A line of symmetry will connect a vertex and a midpoint of an opposite side. It has 7-fold symmetry. A line of symmetry will connect the midpoints of 2 opposite sides.
help me pleaseeeeeeeeeeeee

Answers
Answer:
Step-by-step explanation:
1. Since we know that Lila wants to use 1 cup of pretzels, we can multiply 1/2 x 1/2, which is 1.
2. Now that we multiplied 1/2 by 1/2, we have to multiply 1 1/4 by 1/2.
So 5/4 x 1/2 is 5/8.
3. Lila will need 5/8 cups of raisins.
If a car travels 400 km in 2 hours, how fast is it going? pleasee i need the answer asap
Answers
Answer:
124m/s
Step-by-step explanation:
A baby gains 11 pounds in its first year of life. The baby gained 4 1/4 pounds during the first four months and 3 1/2 pounds in its
second four months. How much did the baby gain in the last four months?
3 1/4pounds
31/2 pounds
4 pounds
5 Pounds
Answers
4.25 plus 3.50 is 7.75
11-7.75 equals 3.25
Suppose a store examines a sample of n =100 purchases and observes 48 customers used a debit card. what is the probability of a sample proportion of 0.48 or less if the true population proportion is 0.60?
Answers
There is a 45.22% chance that a randomly selected sample proportion of 100 purchases will be 0.48 or less.
To find the probability of a sample proportion of 0.48 or less if the true population proportion is 0.60, we can use the sampling distribution of the sample proportion and the z-score.
Given:
Sample size (n) = 100
Observed sample proportion ) = 0.48
True population proportion (p) = 0.60
To find the probability, we need to standardize the observed sample proportion using the z-score formula:
z = ( - p) / √(p * (1 - p) / n)
Substituting the values:
z = (0.48 - 0.60) / √(0.60 * (1 - 0.60) / 100)
= -0.12 / √(0.24 / 100)
= -0.12 / √0.0024
= -0.12 / 0.049
Using a standard normal distribution table or a statistical calculator, we can find the probability associated with the z-score.
The probability of a sample proportion of 0.48 or less, given a true population proportion of 0.60, is the probability to the left of the z-score obtained.
P ≤ 0.48) = P(z ≤ -0.12)
Using a standard normal distribution table, we find that the probability of z ≤ -0.12 is approximately 0.4522.
Therefore, the probability of a sample proportion of 0.48 or less, given a true population proportion of 0.60, is approximately 0.4522 or 45.22%.
This means that there is a 45.22% chance that a randomly selected sample proportion of 100 purchases will be 0.48 or less, if the true population proportion is 0.60.
To know more about randomly refer here:
https://brainly.com/question/13319968#
#SPJ11
4% of ___ days is 56 days
Answers
Answer: 4% of ___days is 56 days Answer If 0.04x = 56 days 0.01x = 14 days x = 14*100 = 1400 days To see more answers head over to College Study Guides
Step-by-step explanation:
I seriously hate my fat finger xd help
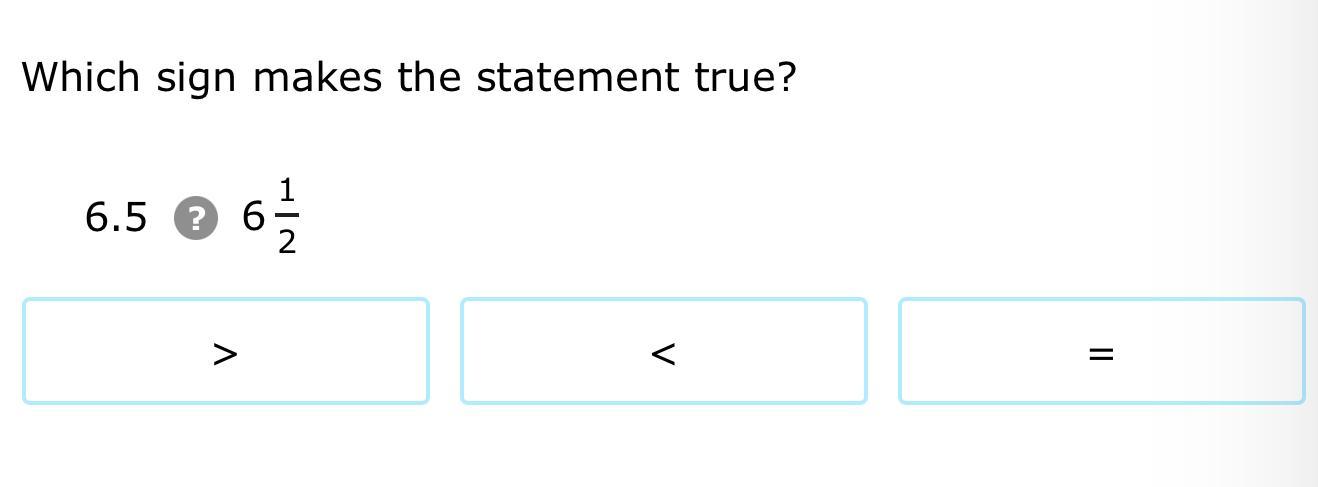
Answers
Answer:
They are equal to one another
Step-by-step explanation:
1/2 is equal to .5, so id you have 6.5 on one side and 6.5 on the other, they are equal.
Answer: =
6 \(\frac{1}{2}\) = 50/100
=6.5
so 6.5 = 6 \(\frac{1}{2}\)
Is the following relation a function?
Relation:
Х Y
6 8
5 1
6 6
2 4
The domain:
{2,5,6}
The range:
{1,4,6,8}
Answers
Answer: No
Step-by-step explanation:
The domain consists of the numbers 6, 5, 6, 2
6 is repeated twice
The criteria for a function is that there are no repeating numbers in the domain
This does not follow the criteria, therefore this is not a function
Answer-No
Analytic geometry
Two of the vertices of an equilateral triangle are the points
(-2,0) and (0,2). Find the coordinates of the third vertex
My idea is to equate the equation of the distance between two
Answers
The coordinates of the third vertex of the equilateral triangle will be (x1, y1) and (x2, y2).
To find the coordinates of the third vertex of an equilateral triangle, given two of its vertices, we can use the concept of equidistant points.
In an equilateral triangle, all three sides have the same length, and the distance between any two vertices is equal.
Let's consider the given vertices as A(-2, 0) and B(0, 2). To find the third vertex, let's denote it as C(x, y).
Using the distance formula, we can set up two equations to equate the distances between the vertices:
1. Distance between A and B:
AB = AC
2. Distance between B and C:
BC = AC
Using the distance formula, the equations become:
1. \(\sqrt{(x+2)^2 + (y-0)^2} = \sqrt{(-2-0)^2 + (0-2)^2}\)
2. \(\sqrt{(x-0)^2 + (y-2)^2} = \sqrt{(0+2)^2 + (2-0)^2}\)
Simplifying these equations, we have:
1. \((x+2)^2 + y^2 = 4 + 4\)
2. \(x^2 + (y-2)^2 = 4 + 4\)
Simplifying further:
1. \(x^2 + 4x + y^2 = 8\)
2. \(x^2 + y^2 - 4y + 4 = 8\)
Rearranging the equations, we get:
1. \(x^2 + 4x + y^2 = 8\)
2. \(x^2 + y^2 - 4y = 4\)
Now, we can solve these two equations simultaneously to find the coordinates (x, y) of the third vertex.
By subtracting equation 2 from equation 1, we eliminate the squared terms:
\(4x + 4y = 4\)
Dividing by 4, we get:
\(x + y = 1\)
Now, we substitute this value in either equation 1 or 2:
\(x^2 + y^2 - 4y = 4\)
Substituting \(x = 1 - y\), we have:
\((1 - y)^2 + y^2 - 4y = 4\)
Expanding and simplifying:
\(1 - 2y + y^2 + y^2 - 4y = 4\)
Combining like terms:
\(2y^2 - 10y + 1 = 4\)
Rearranging the equation:
\(2y^2 - 10y - 3 = 0\)
Now, we can solve this quadratic equation to find the values of y. Once we have the value(s) of y, we can substitute it back into \(x = 1 - y\) to find the corresponding x-coordinate.
Solving the quadratic equation, we get two values of y, let's denote them as y1 and y2. Substituting these values back into \(x = 1 - y\), we get two corresponding x-values, x1 and x2.
Therefore, the coordinates of the third vertex of the equilateral triangle will be (x1, y1) and (x2, y2).
to learn more about equilateral triangle.
https://brainly.com/question/30176141
#SPJ11
Which one of the following is among the major reasons that exponential smoothing has become well accepted as a forecasting technique?Accurate and easy to useSophistication of analysisPredicts turning pointsCaptures patterns in historical dataAbility to Forecast lagging data trends
Answers
The major reason that exponential smoothing has become well accepted as a forecasting technique is its accuracy and ease of use.
Exponential smoothing is a popular method for forecasting time series data because it is simple to implement, requires minimal computational resources, and can produce accurate forecasts for a wide range of time series data.
Additionally, exponential smoothing models can be easily updated with new data, making them well suited for real-time forecasting applications.
This makes exponential smoothing an appealing option for many businesses and organizations looking to make accurate forecasts without the need for complex or expensive analysis tools.
To know more about exponential smoothing click on below link:
https://brainly.com/question/30265998#
#SPJ11
f(x) = 2x2. What is f(3)?
Evaluate the function for the given input
Answers
Answer:
f(3) = 12
Step-by-step explanation:
F(x) = 2x2. What is f(3)
f(3) = 2(3) 2
= 6x2
= 12
f(3) = 12
Help pls!!!
Find the sum of the first 30 terms of the following series, to the nearest integer.
5, 10, 15, ...
Answers
Sketch the integrand. Evaluate the integral geometrically in terms of Area for ∫(4x-2)dx from [-2, 2].The integrand of this integral is .
Answers
The integral ∫(4x - 2)dx from [-2, 2] is equal to the area between the x-axis and the function 4x - 2 over the interval [-2, 2], which is 32.
The integrand is 4x - 2.
To evaluate the integral geometrically in terms of area, we can interpret the integral as the area between the x-axis and the function 4x - 2 over the interval [-2, 2]. We can break this area into two parts: the area under the line y = 4x and the area under the line y = 4x - 2.
The area under the line y = 4x is given by the integral ∫4x dx from -2 to 2, which is equal to [2x^2] from -2 to 2, or 2(2^2) - 2(-2^2) = 16.
The area under the line y = 4x - 2 is given by the integral ∫(4x - 2) dx from -2 to 2, which is equal to [2x^2 - 2x] from -2 to 2, or 2(2^2) - 2(2) - [2(-2^2) - 2(-2)] = 8 - (-8) = 16.
Therefore, the total area between the x-axis and the function 4x - 2 over the interval [-2, 2] is 16 + 16 = 32.
So, the integral ∫(4x - 2)dx from [-2, 2] is equal to the area between the x-axis and the function 4x - 2 over the interval [-2, 2], which is 32.
Learn more about integral:
https://brainly.com/question/28974097
#SPJ11
Given circle B below, find the value of x.
(3x + 10)
(2x - 17)

Answers
Answer: 44
Step-by-step explanation:
since the inscribed angle is half of true arc measure, (3x+10)= 2(2x-17).
when you work this out, you get 44 as x.
The value of x from the given figure is 44°. Therefore, option B is the correct answer.
What is relation between angle at the center and the angle at the circumference?The angle subtended by an arc at the center is twice the angle subtended at the circumference . More simply, the angle at the center is double the angle at the circumference.
From the given figure,
Angle at circumference is (2x-17)° and angle at center is (3x+10)°.
Now, (3x+10)°=2(2x-17)°
3x+10=4x-34
4x-3x=10+34
x=44°
Therefore, option B is the correct answer.
To learn more about the circle theorems visit:
https://brainly.com/question/19906313
#SPJ6
The steepness of a road is called its grade. The higher the grade, the steeper the road is. For example, an interstate highway is considered out of standard if its grade exceeds 7%. Interpret a grade of 7% in terms of slope. Use feet to explain the meaning for a driver.
Answers
Answer:
A grade of 7% = 7 / 100 ;
This means that the elevation or vertical heighy of the interstate highway changes 7 feets for every 100 feets of horizontal distance moved
Step-by-step explanation:
Given that :
A road has a grade of 7%. This means that the slope of the of the highway is 7%. The slope is the proportion of rise and run. Hence the change in vertical distance with horizontal distance moved.
A grade of 7% = 7 / 100 ;
This means that the elevation or vertical heighy of the interstate highway changes 7 feets for every 100 feets of horizontal distance moved
PLEASE HELP!!!
Can you name the angle pairs and type the correct code?

Answers
Answer:
E
G
A
I
Step-by-step explanation:
A sleep study was given to 15 randomly selected people between the ages of 1 and 16. The graph shows the relationship between the age of the person and the number of hours they slept.
scatter plot plane titled Sleep Study with the x axis labeled age in years and the y axis labeled time in hours, with points at 1 comma 8, 2 comma 8 and a half, 3 comma 9 and a half, 4 comma 11, 5 comma 11 and a half, 6 comma 11, 7 comma 11, 8 comma 12, 9 comma 13, 10 comma 13, 11 comma 11 and a half, 12 comma 12 and a half, 13 comma 13 and a half, 15 comma 12, 15 comma 13
Which of the following describes the pattern of association between the variables, based on the graph?
There is a positive linear association.
There is a positive nonlinear association.
There is a negative linear association.
There is a negative nonlinear association.
Answers
Option B "There is a positive nonlinear association" describes the pattern of association between the variables.
What is scatter plot?A scatter plot is a kind of graph that uses a coordinate system to show the values of two variables as points. Each point addresses a perception in the informational index, with the upsides of one variable deciding the situation on the level hub and the upsides of the other variable deciding the situation on the upward pivot.
Based on the scatter plot, it appears that there is a positive nonlinear association between age and the number of hours slept. The points on the graph follow a general upward trend, but the rate of increase slows down as age increases.
Therefore, option B "There is a positive nonlinear association" describes the pattern of association between the variables.
To know more about scatter plot, visit:
https://brainly.com/question/28605735
#SPJ1
Suppose that the following constraints have been provided linear programing model with decision variables xl and x2. -2x1 + 3x2 leq 12 -3x1 + 2x2 leq 12 and x1 leq 0, x2 leq 0. (a) Demonstrate graphically that the feasible region is unbounded. (b) If the objective is to maximize Z = ?x1 + x2, does the model have an optimal solution? If so, find it. If not, explain why not. (c) Repeat part (b) when the objective is to maximize Z = x1 ? x2. (d) For objective functions where this model has no optimal solution, does this mean that there are no good solutions according to the model? Explain. What probably went wrong when formulating the model? D.1 (e) Select an objective function for which this model has no optimal solution. Then work through the simplex method step by step to demonstrate that Z is unbounded. (f) For the objective function selected in part (e), use a software package based on the simplex method to determine that Z is unbounded.
Answers
(a) To demonstrate graphically that the feasible region is unbounded, we can plot the given constraints on a graph. The first constraint, -2x1 + 3x2 ≤ 12, can be represented by a line. The second constraint, -3x1 + 2x2 ≤ 12, can also be represented by a line. Additionally, we have the constraints x1 ≤ 0 and x2 ≤ 0, which define the non-positive regions of the x1 and x2 axes, respectively. By combining these constraints, we can see that there are no upper bounds on the feasible region in the positive direction for either x1 or x2. This indicates that the feasible region is unbounded.
(b) When the objective is to maximize Z = 4x1 + x2, the model does not have an optimal solution. Since the feasible region is unbounded, we can continuously increase the values of x1 and/or x2, resulting in an infinitely increasing objective function value. Therefore, there is no maximum value for Z in this case.
(c) When the objective is to maximize Z = x1 - x2, the model also does not have an optimal solution. Similar to part (b), the feasible region being unbounded allows us to continuously increase the values of x1 and/or decrease the values of x2, resulting in an infinitely increasing objective function value. Thus, there is no maximum value for Z.
(d) The fact that the model does not have an optimal solution does not mean that there are no good solutions according to the model. It simply implies that the objective function cannot be maximized or minimized within the given constraints. There could still be feasible solutions that satisfy the constraints, but they do not result in an optimal value for the objective function.
(e) To select an objective function for which the model has no optimal solution, we can consider an objective such as Z = x1 + x2. Using the simplex method step by step, we would observe that the algorithm does not terminate and continues to iterate indefinitely. This indicates that Z is unbounded, as the objective function value can increase without bound.
(f) Using a software package based on the simplex method, we can confirm that Z is unbounded for the selected objective function. The software would iterate through the simplex algorithm and indicate that the solution is unbounded, meaning there is no maximum or minimum value for the objective function within the given constraints.
To learn more about objective function click here : brainly.com/question/11206462
#SPJ11
Please help me with edge question .

Answers
\(~\hspace{7em}\textit{negative exponents} \\\\ a^{-n} \implies \cfrac{1}{a^n} ~\hspace{4.5em} a^n\implies \cfrac{1}{a^{-n}} ~\hspace{4.5em} \cfrac{a^n}{a^m}\implies a^na^{-m}\implies a^{n-m} \\\\[-0.35em] ~\dotfill\\\\ (4)^{\frac{-4}{2}} \implies (4)^{-2}\implies 4^{-2}\implies \cfrac{1}{4^2}\implies \cfrac{1}{16}\)
evaluate the integral. (use c for the constant of integration.) e− cos(8) d
Answers
The integral of e^(-cos(8)) can't be evaluated using elementary functions. However, it can be expressed in terms of the special function called the exponential integral function, denoted as Ei(x). The integral is equal to Ei(cos(8)) + C, where C is the constant of integration.
Unfortunately, there is no straightforward way to integrate e^(-cos(8)) using elementary functions. The function e^(-cos(x)) is known as the Fourier transform of the Bessel function of the first kind of order zero. This function does not have an elementary antiderivative, which means that we need to use alternative methods to evaluate the integral.
One possible way to express the solution is by using the special function Ei(x), known as the exponential integral function. This function is defined as:
Ei(x) = -∫(-x, ∞) e^(-t)/t dt
Using this function, we can write the integral of e^(-cos(8)) as:
∫ e^(-cos(8)) dx = Ei(cos(8)) + C
where C is the constant of integration. This result holds true for any value of x, not just x=8.
To understand this result better, note that Ei(x) is a well-studied function in mathematics and has many important applications in physics, engineering, and statistics. It is closely related to other special functions such as the logarithmic integral and the gamma function. The function Ei(x) can be expressed in terms of other elementary functions, but these expressions are usually more complicated than the original definition. In conclusion, the integral of e^(-cos(8)) can't be evaluated using elementary functions. However, we can express the solution in terms of the special function Ei(x). The result is Ei(cos(8)) + C, where C is the constant of integration. The function Ei(x) is an important special function in mathematics, with many applications in various fields of science.
Learn more about Bessel function here: brainly.com/question/31412426
#SPJ11
What is the rate of change seen in the graph below?

Answers
(WORK SHOWN BELOW)

the angle from a lookout at the top of a lighthouse (a) boat located at point c is 30 angle the boat travels towards the lighthouse and after 1 minute has travelled a distance of 50 meter and is now located at point b. the angle of elevation from the boat at b up to the lighthouse lookout is 60 angle. find the height of the lighthouse and find the speed of the boat in meters per second from c to b
Answers
We can use the fact that angle ACB is 30° to find v. We can use the tangent function:DB = CD - 50
DB = 2950 / v
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles.
To solve this problem, we will use trigonometry and geometry.
First, let's draw a diagram to better understand the situation:
/|
/ |
/ | h
b / |
----
d
a c
|\ |
| \ |
H | \ h' |
| \ |
| \ |
| \ |
| \ |
| \ |
| \|
------------
D
In this diagram, we have the lighthouse at point A with height H, the boat at point C, and after traveling for 1 minute at a constant speed, it reaches point B. We are given that angle ACB is 30°, angle AHB is 90°, and angle ABH is 60°.
We need to find the height of the lighthouse and the speed of the boat from C to B.Let's start by finding the height of the lighthouse. We can use the tangent function:
tan(ABH) = H / d
tan(60) = H / d
sqrt(3) = H / d
H = sqrt(3) * d
Now, let's find the distance d. We can use the law of cosines:scss
d² = h² + (AB)² - 2 * h * AB * cos(ABH)
We know that AB = 50 meters, ABH = 60°, and h = CD - h', where CD is the distance the boat traveled from C to D and h' is the height of the boat at point D. We can also use the tangent function to find h':
tan(ACH) = h' / CD
tan(30) = h' / (CD + DB)
1/sqrt(3) = h' / (CD + 50)
h' = (CD + 50) / sqrt(3)
Substituting h' in the previous equation:
d² = (CD - (CD + 50) / sqrt(3))² + 50² - 2 * (CD - (CD + 50) / sqrt(3)) * 50 * cos(60)
d² = (CD² + 2 * CD * 50 / sqrt(3) + 2500 / 3) + 2500 - (CD² - CD * 50 / sqrt(3) + 2500 / 3)
d² = 10000 / 3 + CD * 100 / sqrt(3)
Finally, we can use the fact that angle ACB is 30° to find v. We can use the tangent function:
tan(ACB) = h' / (CD + DB)
tan(30) = (CD + 50) / sqrt(3) / (CD + DB)
1 / sqrt(3) = (CD + 50) / sqrt(3) / (CD + DB)
DB = CD - 50
DB = 2950 / v
To learn more about trigonometry from the given link:
https://brainly.com/question/29002217
#SPJ1
Tell whether the angle measures can be those of a triangle.
20°, 160°, 20°
Yes, can be those of a triangle.
No, cannot be those of a triangle.
Answers
No.
The 3 angles of a triangle need to equal 180 degrees.
The sum of the 3 given angles is greater than 180 ( 160 + 20 + 20 = 200) so it cannot form a triangle.
If the two figures are congruent, which statement is true?
A. BCDA ≅ FEHG
B. ABCD ≅ EFGH
C. BADC ≅ EFGH
D. ADCB ≅ HGFE

Answers
Answer:
A
Step-by-step explanation:
the order of letter should resemble the same shape
(Ch 8.2) True or False? In any random sample drawn from a population, the sample mean is an unbiased estimator of the population mean.
11. (Ch 8.2) A consistent estimator for the population mean a. collapses on the true parameter μ as the variance increases. b. collapses on the true parameter μ as the sample size increases. c. consistently follows a normal distribution. d. is impossible to obtain using real sample data.
12. (Ch 8.3) The Central Limit Theorem (CLT) implies that a. the population will be approximately normal if the sample size n is at least 40. b. repeated samples must be taken to obtain normality. c. the distribution of the sample mean is approximately normal for a large n. d. the sample mean is not an unbiased estimator of the population mean.
13. (Ch 8.3) True or False? The Central Limit Theorem says that, if the sample size n exceeds 30, then it must be the case that the population will be normal.
14. (Ch 8.4) True or False? A higher confidence level leads to a narrower confidence interval.
T
B
C
F
F
Answers
True , In any random sample drawn from a population, the sample mean is an unbiased estimator of the population mean.
What is the central limit theorem formula?
The central limit theorem gives a formula for the sample mean and the sample standard deviation when the population mean and standard deviation are known. This is given as follows: Sample mean = Population mean = μ μ Sample standard deviation = (Population standard deviation) / √n = σ / √n.
learn more about of central limit theorem here
https://brainly.com/question/18403552
#SPJ4
What is the slope of (-9,4) (-12,8)?
Answers
Answer: -5/3
Step-by-step explanation:
Answer: m = -4/3
Step-by-step explanation:
If you're given two different coordinates, and you want to find the slope, the general rule is that you subtract the first coordinates from the first. The formula for these kinds of problems is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) .
Rugged cabin co. provides pre-made materials to build cabins. to ensure materials are in supply and ready for quick delivery, the company offers cabins in only three sizes. each cabin has rectangular floor plan where the length is equal to 5 feet more than twice the width. which expression represents the area, in square feet, for each cabin size?A. 2w^2 + 5w, where w is the widthB. 2w^2 + 5, where w is the widthC. 2w^2, where w is the widthD. 10w^2 + 5 w, where w is the width
Answers
The expression that represent the area of the cabin for rectangular floor plan is 2w² + 5w.
What is the area of rectangular shape?
In essence, the area of a rectangle is equal to the sum of its length and breadth. In contrast, the circumference of a rectangle is equal to the product of its four sides. Consequently, we can say that the area of a rectangle equals the space enclosed by its perimeter.
Given that the length of a cabin is equal to 5 feet more than twice the width.
Assume that the width of the cabin be w.
Then the mathematical expression of twice the width is 2w.
Then the mathematical expression of 5 feet more than twice the width is 2w + 5.The length of the cabin is 2w + 5 feet.
The area of rectangular shape is product of length and width.
The area of the cabin is (2w + 5)w
Apply distributive property:
= 2w × w + 5 × w
= 2w² + 5w
To learn more about expression click on below link:
https://brainly.com/question/11516438
#SPJ1
Find the area of ABC with verticles A(4,-3), B(9,-3) and C(10,-11)
Answers
Answer:
Step-by-step explanation:
The area of the triangle when the vertices of the triangle are given can be calculated by the following formula:
Area of triangle = 0.5 * |Ax(By - Cy) + Bx(Ay - Cy) + Cx(Ay - By)| where the vertices are A(Ax, Ay), B(Bx, By), C(Cx, Cy)
Now, we have been given the values of vertices as A(4, -3) B(9,-3) , and C(10, −11)
Therefore,
By applying the formula and substituting the given values, we get
Area = 0.5 * |4 * (-3 + 11) + 9 * (-3 + 11) + 10 * (-3 - 3)|
Area = 0.5 * |44|
Area = 22
Hence, the area of triangle ABC with the given vertices is 22 square units
To know more about the areas of triangle visit the link:
https://brainly.com/question/24207603