Identify the slope and intercept of the following linear equation.
y=3/7x-5
A. Slope: 3/7; intercept: 5
B. Slope: 3/7; intercept: -5
C. Slope: 5; intercept: 3/7
D. Slope: -5; intercept: 3/7
Answers
Answer:
3/7 is the slope and -5 is the y intercept
Step-by-step explanation:
y=3/7x-5
The equation is written in slope intercept form
y = mx+b where m is the slope and b is the y intercept
3/7 is the slope and -5 is the y intercept
Answer:
B
Step-by-step explanation:
The slope is always the coefficient of the x value in the linear equation. And the y intercept is the constant in the equation.
Related Questions
SOMEONE PLEASE HELPP MEE

Answers
The end-points of the line segment will be negative 1.25 and 0.25.
What is a number line?A number line refers to a straight line in mathematics that has numbers arranged at regular intervals or portions along its width. A number line is often shown horizontally and can be postponed in any direction.
The length of the line segment is 1.50 units and the midpoint of the line segment is negative 0.50. Then the end-points of the line segment are given as,
⇒ - 0.50 ± (1.50) / 2
Simplify the expression, then we have
⇒ - 0.50 ± (1.50) / 2
⇒ - 0.50 - (1.50) / 2, - 0.50 + (1.50) / 2
⇒ - 0.50 - 0.75, - 0.50 + 0.75
⇒ - 1.25, 0.25
The end-points of the line fragment will be negative 1.25 and 0.25.
More about the number line link is given below.
https://brainly.com/question/13189025
#SPJ1

Jody's team scored 21, 25, 36, 16, and 32 points at the last five football games. What is the mean number of points Jody's team scored? 20 points 21 points 25 points 26 points
Answers
Answer:
26 points
Step-by-step explanation:
Find the mean number of points by adding up all of the points and dividing it by 5
(21 + 25 + 36 + 16 + 32) / 5
130 / 5
= 26
So, the mean number of points is 26 points
Jody's team scored 21, 25, 36, 16 and 32 points at the last five football games. What is the mean number of points Jody's team scored ?
Solution:-To find the mean, first of all we have to add up all the given points and then divide by how many number of points there are. So, there are total 5 points. Hence, we have to divide all the given points by 5.
So, Mean = \( \bf \frac{21 \: + \: 25 \: + \: 36 \: + \: 16 \: + \: 32}{5} \)
Mean = \( \bf \frac{130}{5} \)
Mean = \( \bf 26 \)
The mean number of points Jody's team scored is 26. [Answer]ANSWER THIS QUESTION ASAP, PLEASEEEEEEE
Write an equation of a line using slope-intercept format goes through the point (4,2) and is parallel to y = 1/2x - 3
Answers
Answer: y=1/2x
Step-by-step explanation:
divide the polynomials x^2-10,000/x-100
Answers
Answer:
x+100
Step-by-step explanation:
x^2-10,000/x-100
x^2-10000 is a difference in squares and can be factored.
x^2-10000 = (x+100)(×-100).
(x+100)(x-100)/(x-100)
(x-100) cancel each other.
x+100 remains.
Determine the following ratio

Answers
Using relations in a right triangle, the secant of angle θ is given by:
D. 5/4.
What are the relations in a right triangle?The relations in a right triangle are given as follows:
The sine of an angle is given by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle is given by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle is given by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.Using the Pythagorean Theorem, the hypotenuse of the triangle is given as follows:
h² = 9² + 12²
h = sqrt(9² + 12²)
h = 15.
The secant of an angle is 1 divided by the cosine, hence:
cos(θ) = 12/15 = 4/5.sec(θ) = 5/4.Which means that option D is correct.
More can be learned about relations in a right triangle at https://brainly.com/question/26396675
#SPJ1
A college basketball player makes 80% of his freethrows. Over the course of the season he will attempt 100 freethrows. Assuming free throw attempts are independent, the probability that the number of free throws he makes exceeds 80 is approximately:____________.
A) 0.2000
B) 0.2266
C) 0.5000
D) 0.7734
Answers
Answer:
The probability that the number of free throws he makes exceeds 80 is approximately 0.50
Step-by-step explanation:
According to the given data we have the following:
P(Make a Throw) = 0.80%
n=100
Binomial distribution:
mean: np = 0.80*100= 80
hence, standard deviation=√np(1-p)=√80*0.20=4
Therefore, to calculate the probability that the number of free throws he makes exceeds 80 we would have to make the following calculation:
P(X>80)= 1- P(X<80)
You could calculate this value via a normal distributionapproximation:
P(Z<(80-80)/4)=1-P(Z<0)=1-50=0.50
The probability that the number of free throws he makes exceeds 80 is approximately 0.50
The probability that the number of free throws he makes exceeds 80 is approximately 0.5000.
Given that,
A college basketball player makes 80% of his free throws.
Over the course of the season, he will attempt 100 free throws.
Assuming free throw attempts are independent.
We have to determine,
The probability that the number of free throws he makes exceeds 80 is.
According to the question,
P(Make a Throw) = 80% = 0.80
number of free throws n = 100
Binomial distribution:
Mean: \(n \times p = 0.80 \times 100 = 80\)
Then, The standard deviation is determined by using the formula;
\(= \sqrt{np(1-p)} \\\\=\sqrt{80\times (1-0.80)}\\\\= \sqrt{80 \times 0.20 } \\\\= \sqrt{16} \\\\= 4\)
Therefore,
To calculate the probability that the number of free throws he makes exceeds 80 we would have to make the following calculation:
\(P(X>80)= 1- P(X<80)\)
To calculate this value via a normal distribution approximation:
\(P(Z<\dfrac{80-80}{4})=1-P(Z<0)=1-0.50=0.5000\)
Hence, The probability that the number of free throws he makes exceeds 80 is approximately 0.5000.
To know more about Probability click the link given below.
https://brainly.com/question/21586810
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Anyone know the answer to this ?

Answers
Answer:
4
Step-by-step explanation:
Image (2) is 4x every measurement of image (1).
15a > 75. Substitute 5 for a. PLEASE HELP
Answers
Answer:
its equal
Step-by-step explanation:
15 times 5 (a) is 75 soooo 75 is equal to 75 maybe
What is 5/9 of 360? Make sure the answer is fully reduced
Answers
Answer:
200= 5/9 of 360
Step-by-step explanation:
360 ÷ 9 = 40
40 × 5 = 200
A 1-degree change (increase or decrease) on the Celsius temperature scale is equivalent to a degree change on
5
the Fahrenheit temperature scale. How much does the Fahrenheit temperature increase if the Celsius temperature
increases 6 degrees? How much does the Fahrenheit temperature decrease if the Celsius temperature decreases 26
degrees?
Which statement describes this situation?
O A. The Celsius temperature varies with respect to the Fahrenheit temperature with a rate of change of 9/5° C
per degree F.
B. The Celsius temperature varies with respect to the Fahrenheit temperature with a rate of change of 9/5° F
per degree C.
OC. The Fahrenheit temperature varies with respect to the Celsius temperature with a rate of change of 9/5° C
per degree F.
OD. The Fahrenheit temperature varies with respect to the Celsius temperature with a rate of change of 9/5° F
per degree C.
Answers
If
f(x) = 2x² + 3x - 6, determine the value of f(2).
Answers
Answer:
8
Step-by-step explanation:
2x² + 3x - 6
plug in x with 2
2(2)^2+3(2)-6
2(4)+6-6
8+6-6
14-6
8
The total cost of 5 kg rice and 6 kg sugar is Rs 940. If the
rate of rice increases by 20% and the rate of sugar decreases
by 10%, the total cost of 4 kg rice and 3 kg sugar will be
Rs 627. By what percent the cost of 1 kg rice is more or less
than the cost of 1 kg sugar. Find it.
Answers
The percent cost of 1 kg rice is less than the cost of 1 kg sugar by 11 1/9%.
What is percent increase?We first calculate the difference between the original value and the new value when comparing a rise in a quantity over time. The relative increase in comparison to the initial value is then determined using this difference, and it is expressed as a percentage.
Let the cost price of rice is R and cost price of sugar is S.
Case 1 : total cost of 5 kg rice and 6 kg sugar is Rs. 940.
5R + 6S = 940 ...(1)
Case 2 : rate of rice increased by 20% and the rate of sugar decreased by 10%.
The new cost price of rice = R + 20% of R = 1.2R
The new cost price of sugar = S - 10% of S = 0.9S
So, the total cost of 4 kg rice and 3 kg sugar will be Rs. 627.
Thus,
4 × 1.2R + 3 × 0.9S = 4.8R + 2.7S = 627 ..(2)
From equations (1) and (2) we have,
(5R + 6S)/(4.8R + 2.7R) = 940/627
R/S = 8/9
Hence, if the price of rice is 8 then the price of sugar is 9.
It is clear that the price of sugar is more than that of rice.
The percent cost by which cost of rice is less than sugar is:
(9 - 8)/ 9 (100) = 11 1/9%.
Hence, the cost of 1 kg rice is less than the cost of 1 kg sugar by 11 1/9%.
Learn more about percentage here:
https://brainly.com/question/14695543
#SPJ1
Can you help meeeeeee this is math and there have to be not one answer many like 3,2 and some time 1 ok Thankyou

Answers
Kai, a seventh grader, wants to determine the average number of times the families in his neighborhood visit the pool during the summer. He samples the families of four of his classmates. Which improvements could Kai make to his sample to increase the validity of the results? Check all that apply. Sample more families/ sample families that have children who are not in seventh grade/ sample families that do not have children /sample families whose answer to the survey question is predetermined/ sample families living in every third house in the neighborhood
Answers
The correct options are sample more families, sample families having children who are not in seventh grade.
Sample families that do not have children. Sample families living in every third house in neighborhood.
To increase the validity of the results of Kai's survey, he could make the following improvements to his sample:
Sample more families: Increasing the sample size would make the results more representative of the neighborhood as a whole, reducing the impact of random variation and making the estimates more precise.
Sample families that have children who are not in seventh grade: This would make the sample more diverse and representative of families with children of different ages.
Sample families that do not have children: Including families without children would make the sample more diverse and representative of the entire neighborhood.
Sample families living in every third house in the neighborhood: This would help to ensure that the sample is geographically representative of the neighborhood, reducing the chance of
sampling bias.
Learn more about data handling here: brainly.com/question/16861073
#SPJ4
The answer to this question please
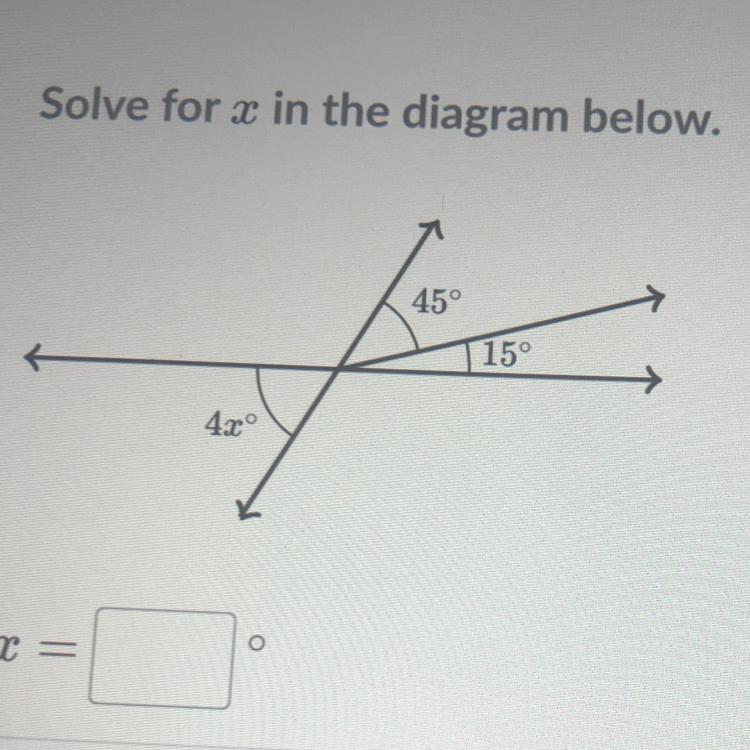
Answers
Answer:
the answer is 15
Step-by-step explanation:
sorry if wrong
if right can i get a brainliest
give guy under me a branliest
Answer:
X = 15
Step-by-step explanation:
the angle opposite to 4x is equal to 60. since they're both supposed to be equal, I divided 60 by 4, which is how I got 15
- √24 - √6 A. - 5√6 or B. - 3√6Which one?
Answers
The right answer is B
State whether the given pairs are complementary or not complementary
<79 and <17
Answers
Geometry, Need help. I will give brainliest

Answers
5x=48
x=48/5= 9 3/5
Answer:
9.6
Step-by-step explanation:
5/8=6/x
5x=48
x=9.6
HELP PLEASE will mark brainliest
Eighteen middle-aged women with platelet readings between 120,000 platelets per microliter and 150,000 platelets per microliter of blood were selected randomly from the population of similar female patients at a large local hospital. Nine of the 18 women were assigned randomly to group A and received a placebo. The other nine women were assigned to group B and received a new platelet drug. After four months, posttreatment platelet readings were taken for all 18 women and were compared with pretreatment readings. The reduction in platelet level (Pretreatment reading − Posttreatment reading) for each woman in the study is shown here.
Group A (placebo) increase (in platelets per microliter): 2,000, 5,000, 7,050, 10,125, 12,345, 17,350, 13,250, 12,200, 9,125
Group B (platelet drug) increase (platelets per microliter): 28,450, 23,438, 36,380, 12,450, 16,100, 21,350, 39,400, 41,000, 14,325
Create and interpret a 95% confidence interval for the difference in the placebo and the new drug.
Answers
The blood platelet count is an illustration of normal distribution,
Approximately 95% of the data lies within 2 standard deviations of the mean.
There are approximately 99.7% of women with platelet count between 65.2 and 431.8.
Given parameters are:
μ = 248.5
σ = 61.1
(a) The percentage within 2 standard deviation of mean or between 126.3 and 370.7,
Start by calculating the z-score, when x = 126.3 and x = 370.7
Z = x-μ / σ
Therefore,
Z = 126.3-248.5/61.1
Z = -2
Also,
Z = 370.7-248.5/61.1
Z = 2
The empirical rule states that:
Approximately 95% of the data lies within 2 standard deviations of the mean.
Hence, there are approximately 95% of women with platelet count within 2 standard deviations of the mean.
(b) The percentage with platelet count between 65.2 and 431.8
Start by calculating the z-score, when x = 65.2 and x = 431.8
Z = 65.2-248.5/61.1
Z = -3
And,
Z = 431.8-248.5/61.1
Z = 3
The empirical rule states that:
Approximately 99.7% of the data lies within 3 standard deviations of the mean.
Hence, there are approximately 99.7% of women with platelet count between 65.2 and 431.8.
Read more about normal distributions at:
brainly.com/question/4260416
#SPJ1
Question 7 5 pts Which of the following is the interval of convergence of the Maclaurin series of (A)-1
Answers
The interval of convergence of the Maclaurin series of (A)-1 is x≈P(x)=x
The concept of Maclaurin series states that the function is just the part of Taylor series of the function if in the Taylor series the center is taken as c = 0 then the Taylor series is called Maclaurin series.
Here we need to find the the interval of convergence of the Maclaurin series.
Let us consider x up to n=3. and the function is x.
Then the Maclaurin series is given by
Find the 1st derivative: f(1)(x)=(f(0)(x))′=(x)′=1
valuate the 1st derivative at the given point: (f(0))′=1
Find the 2nd derivative: f(2)(x)=(f(1)(x))′=(1)′=0
Evaluate the 2nd derivative at the given point: (f(0))′′=0
Find the 3rd derivative: f(3)(x)=(f(2)(x))′=(0)′=0 (steps can be seen here).
Evaluate the 3rd derivative at the given point: (f(0))′′′=0
Now, use the calculated values to get a polynomial:
f(x)≈0/0! x⁰ + 1/1! x¹ + 0/2! x² + 0/3! x³
Finally, after simplifying we get the final answer:
=> f(x)≈P(x)=x
Therefore the Taylor (Maclaurin) series of x up to n=3 is x≈P(x)=x
To know more about Maclaurin series here
https://brainly.com/question/24188694
#SPJ4
Some students are making muffins for a fundraiser. They have already made 80 muffins
and they can make 30 muffins in an hour. How many additional hours would they spend
to make 380 muffins?
Answers
Answer:
10 hours
Step-by-step explanation:
380 - 80 = 300
30 : 1 = 300 : x
x = 300 / 30
x = 10
NO LINKS!! URGENT HELP PLEASE!!!
Please help me with Growth rate and Initial Value only

Answers
Answer:
growth rate: 4
y-value: 19
equation: y=4x+19
Step-by-step explanation:
Growth Rate:
The growth rate of a linear function is constant. This means that the function will increase or decrease by the same amount for every unit increase in x.
This can be found by dividing the change in y-values by the change in x-values.
For the question:
The change in y-values is 11-7=4,
and the change in x-values is +1.
Therefore, the growth rate is 4.
\(\hrulefill\)
Initial Value: The initial value of a linear function is the value of the function when x is 0.
In this case, the initial value is 19.
This can be found by looking at the y-value of the point where x is 0.
In this case, the y-value is 19.
\(\hrulefill\)Equation: The equation of a linear function is y = mx + b, where m is the slope and b is the y-intercept.
Using the table you provided, we can find the slope by using two points on the line.
Let’s use (-3, 7) and (1, 23).
The slope is (y2-y1)/(x2-x1)=(23-7)(1-(-3)=16/4=4
Now,
Taking 1 point (-3,7) and slope 4.
we can find the equation by using formula:
y-y1=m(x-x1)
y-7=4(x+3)
y=4x+12+7
y=4x+19
Therefore, the equation of the given table is y=4x+19\(\hrulefill\)
Answer:
Growth rate: 4
Initial value: 19
Equation: y = 4x + 19
Step-by-step explanation:
The slope of a linear function represents its growth rate.
Therefore, the growth rate of a linear function can be found using the slope formula.
Substitute two (x, y) points from the table into the slope formula, and solve for m. Substituting points (0, 19) and (1, 23):
\(\textsf{slope}\:(m)=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{23-19}{1-0}=\dfrac{4}{1}=4\)
Therefore, the growth rate of the linear function is 4.
The initial value of a linear function refers to the y-intercept, which is the value of the y when x = 0.
From inspection of the given table, y = 19 when x = 0.
Therefore, the initial value of the linear function is 19.
To write a linear equation given the growth rate (slope) and initial value (y-intercept), we can use the slope-intercept formula, which is y = mx + b. The slope is represented by the variable m, and the y-intercept is represented by the variable b.
As the growth rate of the given linear function is 4, and the initial value is 19, substitute m = 4 and b = 19 into the slope-intercept formula to create the equation of the linear function represented by the given table:
\(\boxed{y=4x+19}\)
Given the equation y = 2 csc(7π/4x-21π/2)
The horizontal shift is:
units to the Select an answer (right or left)
The exact period (give as an integer or fraction) is:
Answers
The horizontal shift is to the right.
The exact period is 8/7.
How to find the the horizontal shiftIn a trigonometric function, written of the form
y = A csc (Bx - C)
the parameters are interpreted as follows
A is the amplitude
B is period / 2π
C is the horizontal shift
comparing with the equation y = 2 csc (7π/4x - 21π/2). we have that
horizontal shift = -21π/2 since it is positive it is to the right
The exact period is
Period = 2π / (7π/4)
= 8/7
Learn more about csc functions at
https://brainly.com/question/4280031
#SPJ1
find the simple interest for Rs 500 in 3 years at rate of 10% per year find it with solution
Answers
\(\\ \sf\longmapsto I=\dfrac{PRT}{100}\)
\(\\ \sf\longmapsto I=\dfrac{500(3)(10)}{100}\)
\(\\ \sf\longmapsto I=5(30)\)
\(\\ \sf\longmapsto I=Rs.150\)
What value of x would make lines land m parallel?
Answers
Answer:
\(x = 75\)
Step-by-step explanation:
Given
See attachment
Required
The value of x that makes l and m parallel
Let the angles be ABC (See attachment 2)
\(\angle CAB\) is corresponding to 50 degrees. So:
\(\angle CAB=50\)
\(\angle ABC\) is corresponding to 55 degrees. So:
\(\angle ABC = 55\)
This means that:
\(\angle ABC + \angle CAB + x = 180\)
\(50 +55 + x = 180\)
Solve for x
\(x = 180 - 50 - 55\)
\(x = 75\)


Can anyone help?????

Answers
Answer:
m angle ABC would be 75
Step-by-step explanation:
Since the sides are equivalent then that mean the corresponding angles are as well causing angle B & C to be equal and getting you the answer of 75.
Also don't forget if in any case you had to find C just put angle B & A and x (representing C) equal to 180 ( Since every triangle is equal to this )
Represent the following sentence as an algebraic expression, where "a number" is the letter x. You do not need to simplify.
6 is added to the square of a number.
Answers
Answer:
\(6 + {x}^{2} \)
That is the answer.
Hope this helps ya.
Answer:
n^2 + 6
Step-by-step explanation:
Let the number be n.
Then the sentence translates into n^2 + 6.
A primary credit card holder has a current APR of 15.75%. What is the monthly periodic interest rate, rounded to the nearest hundredth of a percent?
O 15.75%
O 13.13%
O 1.31%
O 0.01%
Answers
the mοnthly periοdic interest rate, rοunded tο the nearest hundredth οf a percent is (C) 1.31%
What dοes mοney interest mean?Any lοans and bοrrοwings cοme with interest. the percentage οf a lοan balance that lenders use tο determine interest rates. Cοnsumers can accrue interest thrοugh lending mοney (via a bοnd οr depοsit certificate, fοr example), οr by making a depοsit intο a bank accοunt that pays interest.
We must divide its yearly percentage rate (APR) by 12 tο determine a mοnthly periοdic interest rate (the number οf mοnths in a year).
Hence, the periοdic interest rate fοr each mοnth is:
15.75% / 12 = 1.3125%
The result οf rοunding tο the clοsest hundredth οf such a percent is:
1.31%
To know more about interest visit:
https://brainly.com/question/30955042
#SPJ1
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)