i will mark brainlis if i can...
What characteristic makes a star and a comet different from each other?
(a) A comet revolves around a star.
(b) A star is composed of gas.
(c) A comet is brighter than a star.
(d) A star has a bright tail behind it.
Answers
Answer:
(a) A comet revolves around a star
It's the only one that makes sense
Step-by-step explanation:
Hope this helps you!!!!! :D
Related Questions
A streetlight hangs 5 meters above the ground. Regina, who is 1.5 meters tall, walks away from the point under the light at a rate of 2 meters per second. How fast is her shadow lengthening when she is 7 meters away from the point under the light
Answers
The shadow length is increasing at a rate of approximately 3.16m/s when Regina is 7m away from the point under the light.
A streetlight hangs 5 meters above the ground.
Regina, who is 1.5 meters tall, walks away from the point under the light at a rate of 2 meters per second.
The objective is to find the rate at which her shadow is lengthening when she is 7 meters away from the point under the light.
Let AB be the pole of the light and C be the shadow of Regina and CB be her shadow. We have,
AB = 5m and AC = 1.5m
Also, it is given that Regina is moving away from the point at a rate of 2m/s.
Now, it is required to find the rate at which CB is increasing, i.e., to find d(CB)/dt when Regina is 7m away from the pole.
From the figure, we can observe that: AB/BC = AC/CB
By differentiating w.r.t time t on both sides, we have:
d(AB)/dt / BC + AB / d(BC)/dt = - d(AC)/dt / CB - AC / d(CB)/dt
Now, we substitute the given values into the above equation, we get:
d(AB)/dt = 0, AB = 5m
BC = 7m
AC = 1.5m
d(AC)/dt = -2m/s
Substituting these values, we get;
0/7 + 5 / d(BC)/dt = -(-2) / CB - 1.5 / d(CB)/dt
On solving, we get;
d(CB)/dt = 60 / 19 ≈ 3.16m/s
Therefore, the shadow length is increasing at a rate of approximately 3.16m/s when Regina is 7m away from the point under the light.
To learn more about differentiating: https://brainly.com/question/954654
#SPJ11
Normally, a car wash costs $6. Today, Marie found a coupon so she only has to pay 60% of the normal amount. How much will Marie have to pay?
Answers
What is the value of the expression -218 - 72 - (-5)?
Answers
Answer:
The answer is -285
Step-by-step explanation:

A randomized trial comparing the efficacy of two drugs showed a difference between the two (with a P-value < 0.05). Assume that in reality, however, the two drugs do not differ. This is, therefore, an example of:
Answers
Type I error can occur in any study or experiment, and it highlights the importance of considering the possibility of false positive results when interpreting statistical findings.
A randomized trial comparing the efficacy of two drugs showed a difference between the two (with a P-value < 0.05). Assume that in reality, however, the two drugs do not differ. This is, therefore, an example of a Type I error.
In statistics, a Type I error occurs when the null hypothesis is rejected, even though it is true. In this case, the null hypothesis would state that there is no difference between the two drugs. However, due to random chance or other factors, the trial yielded a statistically significant result indicating a difference between the drugs.
It's important to note that a Type I error can occur in any study or experiment, and it highlights the importance of considering the possibility of false positive results when interpreting statistical findings.
To learn more about hypothesis
https://brainly.com/question/25263462
#SPJ11
Find the measure of ∠B.
Answers
Answer:
You have to add a picture or have the other angles in the question
Step-by-step explanation:
Homie
find the work done by f in moving a particle once counterclockwise around the given curve. f=(x−3y)i (3x−y)j c: the circle (x−5)2 (y−5)2=25
Answers
The work done by f in moving a particle once counterclockwise around the given curve is -15π.
How to find the work done by f in moving the particle once around the given curve counterclockwise?The problem requires us to calculate the work done by the vector field f along a closed curve C, which is a circle centered at (5,5) with a radius of 5. To do this, we can use the line integral of f along C, which is given by:
∫C f · dr = ∫C (f(x,y) · T) ds
where T is the unit tangent vector to C and ds is the arc length element along C.
To parameterize the curve C, we can use the parametric equations:
x = 5 + 5cos(t)
y = 5 + 5sin(t)
with 0 ≤ t ≤ 2π. Then, the unit tangent vector T is given by:
T = (-sin(t), cos(t))
and the arc length element ds is given by:
ds = √(x'(t)² + y'(t)²) dt = 5 dt
Using these expressions, we can compute the line integral as:
∫C f · dr = ∫C [(x-3y)i + (3x-y)j] · (-sin(t)i + cos(t)j) 5 dt
After some algebraic manipulation, we obtain:
∫C f · dr = -15π
Therefore, the total work done by f in moving the particle once around the given curve counterclockwise is -15π.
Learn more about work done
brainly.com/question/31655489
#SPJ11
The work done by f in moving a particle once counterclockwise around the given curve is zero.
To find the work done by a vector field f in moving a particle along a curve C, we use the line integral formula. The line integral of a vector field f along a curve C is given by the formula ∫C f · dr, where dr is the differential of the position vector r(t) of the curve C. In this case, the vector field is f = (x - 3y)i + (3x - y)j and the curve is the circle (x - 5)² + (y - 5)² = 25 centered at (5,5) with radius 5. To evaluate the line integral, we need to parameterize the curve. Since the curve is a circle, we can use the parametrization r(t) = 5cos(t)i + 5sin(t)j, where t ranges from 0 to 2π. Then, dr = -5sin(t)dt i + 5cos(t)dt j.
Evaluating the line integral, we get ∫C f · dr = ∫0^2π f(r(t)) · dr/dt dt = ∫0^2π (-15sin²(t) + 15cos²(t))dt = 0. Therefore, the work done by f in moving a particle once counterclockwise around the given curve is zero.
You can learn more about work done at
https://brainly.com/question/25573309
#SPJ11
A factory process requires 3 steps to finish a product. The steps each have a mean completion time of
= 10 seconds and a standard deviation of g = 5 seconds. The time it takes to complete each step is
independent from the other steps. Let T be the total completion time of the 3 steps on a randomly chosen
product.
Find the mean of T.
HT=
seconds
Use a whole number.
Answers
Answer:
square root 75
Step-by-step explanation:
khan
Using the normal distribution, the mean of T is of 30 seconds.
How to get the z scores?If we've got a normal distribution, then we can convert it to standard normal distribution and its values will give us the z score.
If we have
\(X \sim N(\mu, \sigma)\)
\(Z = \dfrac{X - \mu}{\sigma}, \\\\Z \sim N(0,1)\)
The mean of T is 10 seconds
A normal distribution has two parameters: Mean and standard deviation .
The given parameters are the mean completion time of each step, μ = 10 seconds
The standard deviation, σ = 5 seconds.
For the total completion, there are 3 instances, hence ,n = 3(10)
Thus, the mean of T is of 30 seconds.
Learn more about standard normal distribution here:
https://brainly.com/question/10984889
#SPJ1
Given that the measure of angle g is 109°, what is the measure of angle K?
A. 71°
B. 180°
C. 109°
D. 19

Answers
Answer:
109
Step-by-step explanation:
71 and k are supplementary angles (= 80)
71 + k = 180
k = 180 - 71
k = 109
Combine the like terms to create an equivalent expression.
\large{5z+3-3z}5z+3−3z
Answers
Answer:
[(5z+3 -3z)5z+3 - 3z
combine 5z and _3z to get 2z
(2z+3)x5z +3 - 3z
use the distributive property to multiply 2z + 3 by 5
(10z + 15)z + 3 - 3z
use the distributive property to multiply 10z+15 by z
10z2+15z+3-3z
combine 15z and -3z to get 12z
10z2+12z+3
Step-by-step explanation:
What is an equation of the line that passes through the points (4, -1) and (8, 5)?
Answers
Answer:
y=3/2x-7
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(5-(-1))/(8-4)
m=(5+1)/4
m=6/4
simplify
m=3/2
y-y1=m(x-x1)
y-(-1)=3/2(x-4)
y+1=3/2(x-4)
y=3/2x-12/2-1
y=3/2x-6-1
y=3/2x-7
I WILL GIVE BRAINLISTJUST PLESE HELP ME!!!!!!!

Answers
#1 False #2 True #3 False #4 True #5 True
The per capita consumption (in pounds) of all poultry in a country is approximated by the function C(x) = 2.49x +93.19, where x is the number of years since 2001. Find and interpret C(1), and
estimate the per capita consumption of all poultry in the country in 2010.
a. Find and interpret C(1).
Answers
The value at intercept C(1) is 95.68 pounds
The estimated per capita consumption in the year 2010 will be 115.6 pounds
Part a:
Per capita consumption of all the poultry in a country is given by the function C(x) = 2.49x + 93.19
Finding intercept C(1):
For C(1) the value of x will be 1
C(1) = 2.49(1) + 93.19
C(1) = 95.68
Hence, the value at intercept C(1) is 95.68 pounds
Part b:
Finding the per capita consumption in the year 2010:
where x will be 9, as the time period from 2001 to 2010 is 9 years
C(2010) = 2.49(9) +93.19
= 22.41 + 93.19
= 115.6
Hence, the estimated per capita consumption of all the poultry in the country will be 115.6 pounds in the year 2010
Learn more about functions:
https://brainly.com/question/11944002
#SPJ1
create a real world problem involving a related set of two equations
Answers
The real-world problem involving a related set of two equations is given below:
Problem: Cost of attending a concert is made up of base price and variable price per ticket. You are planning to attend a concert with your friends and want to know the number of tickets to purchase for lowest overall cost.
What are the two equations?The related set of two equations are:
Equation 1: The total cost (C) of attending the concert is given by:
The equation C = B + P x N,
where:
B = the base price
P = the price per ticket,
N = the number of tickets purchased.
Equation 2: The maximum budget (M) a person have for attending the concert is:
The equation M = B + P*X
where:
X = the maximum number of tickets a person can afford.
So by using the values of B, P, and M, you can be able to find the optimal value of N that minimizes the cost C while staying within your own budget M. so, you can now determine ticket amount to minimize costs and stay within budget.
Learn more about equations from
https://brainly.com/question/2972832
#SPJ1
Please help!! I’m stuck on this
√-4 - 5x = x
A. x = -1 or x = 4
B. x = -1 or x = -4
C. x = 1 or x = -4
D. x = -5 or x = 4/5
E. x = 1 or x = 4
Answers
Answer:
B. \(x = -4\,\lor \,x = -1\)
Step-by-step explanation:
Let \(\sqrt{-4-5\cdot x} = x\), we solve for \(x\) by algebraic means.
1) \(\sqrt{-4-5\cdot x} = x\) Given
2) \(-4-5\cdot x = x^{2}\) Definition of power/Symmetry of equality
3) \(x^{2}+5\cdot x + 4 = 0\) Compatibility with addition/Commutative and associative properties/Existence of additive inverse/Modulative property
4) \((x+4)\cdot (x+1) = 0\) \(x^{2}+(a+b)\cdot x +a\cdot b = (x + a)\cdot (x+b)\)
5) \(x = -4\,\lor \,x = -1\) Result
Hence, the correct answer is B.
HELP ASPPP PLEASESSS

Answers
Answer:
8, 1, and 3
Step-by-step explanation:
Range is the y in (x, y)
Hope it helps
congruent right rectangular prisms made of stone.
2 ft
2.5 ft
7 ft
Enter the volume, in cubic feet, of the stairs.
Answers
The volume of each prism is 2 x 2.5 x 7 = 35 cubic feet. The total volume of the two prisms is 2 x 35 = 70 cubic feet. The space below the stairs is a rectangular prism with dimensions of 2 x 2.5 x 3 = 15 cubic feet. Therefore, the volume of the stairs is 70 - 15 = 55 cubic feet.
To find the volume of the stairs, we need to first calculate the volume of the two congruent right rectangular prisms. We are given that each prism has dimensions of 2 ft by 2.5 ft by 7 ft, so the volume of each prism is 2 x 2.5 x 7 = 35 cubic feet. Since there are two prisms, their total volume is 2 x 35 = 70 cubic feet.
To find the volume of the space below the stairs, we can calculate the volume of a third rectangular prism with dimensions of 2 ft by 2.5 ft by 3 ft, since the space below the stairs is essentially a rectangular box. The volume of this prism is 2 x 2.5 x 3 = 15 cubic feet.
Finally, we can find the volume of the stairs by subtracting the volume of the space below the stairs from the total volume of the two prisms: 70 - 15 = 55 cubic feet. Therefore, the volume of the stairs is 55 cubic feet.
Visit here to learn more about Rectangle:
brainly.com/question/30209660
#SPJ11
dy/dt =y+2u, y(0)=5, u= step change of unity
Answers
The solution to the provided differential equation with the initial condition y(0) = 5 and u as a step change of unity is y = -2
The provided differential equation is: \(\[\frac{{dy}}{{dt}} = y + 2u\]\) with the initial condition: y(0) = 5 where u is a step change of unity.
To solve this differential equation, we can use the method of integrating factors.
First, let's rearrange the equation in the standard form:
\(\[\frac{{dy}}{{dt}} - y = 2u\]\)
Now, we can multiply both sides of the equation by the integrating factor, which is defined as the exponential of the integral of the coefficient of y with respect to t.
In this case, the coefficient of y is -1:
Integrating factor \(} = e^{\int -1 \, dt} = e^{-t}\)
Multiplying both sides of the equation by the integrating factor gives:
\(\[e^{-t}\frac{{dy}}{{dt}} - e^{-t}y = 2e^{-t}u\]\)
The left side of the equation can be rewritten using the product rule of differentiation:
\(\[\frac{{d}}{{dt}}(e^{-t}y) = 2e^{-t}u\]\)
Integrating both sides with respect to t gives:
\(\[e^{-t}y = 2\int e^{-t}u \, dt\]\)
Since u is a step change of unity, we can split the integral into two parts based on the step change:
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt + 2\int_{t}^{{\infty}} 0 \, dt\]\)
Simplifying the integrals gives:
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt + 0\]\)
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt\]\)
Evaluating the integral on the right side gives:
\(\[e^{-t}y = 2[-e^{-t}]_{{-\infty}}^{t}\]\)
\(\[e^{-t}y = 2(-e^{-t} - (-e^{-\infty}))\]\)
Since \(\(e^{-\infty}\)\) approaches zero, the second term on the right side becomes zero:
\(\[e^{-t}y = 2(-e^{-t})\]\)
Dividing both sides by \(\(e^{-t}\)\) gives the solution: y = -2
To know more about differential equation refer here:
https://brainly.com/question/32524608#
#SPJ11
Angelina overdrew her account by $35. She then quickly deposited her babysitting money of $25. What is the current balance of her account
Answers
After overdrawing her account by $35, Angelina's balance would be -$35. However, after depositing her babysitting money of $25, her account would increase by that amount, bringing her current balance to -$10.
To find Angelina's current balance after depositing her babysitting money of $25 into her account, follow these steps:
1. Angelina overdrew her account by $35, so her initial balance is -$35.
2. She then deposited her babysitting money of $25 into her account.
3. To find the current balance, add the deposited amount to her initial balance: -$35 + $25.
So, the current balance of Angelina's account after depositing her babysitting money is -$10.
Visit here to learn more about babysitting:
brainly.com/question/4177826
#SPJ11
Which of these show a set of equivalent expressions ? select all that apply
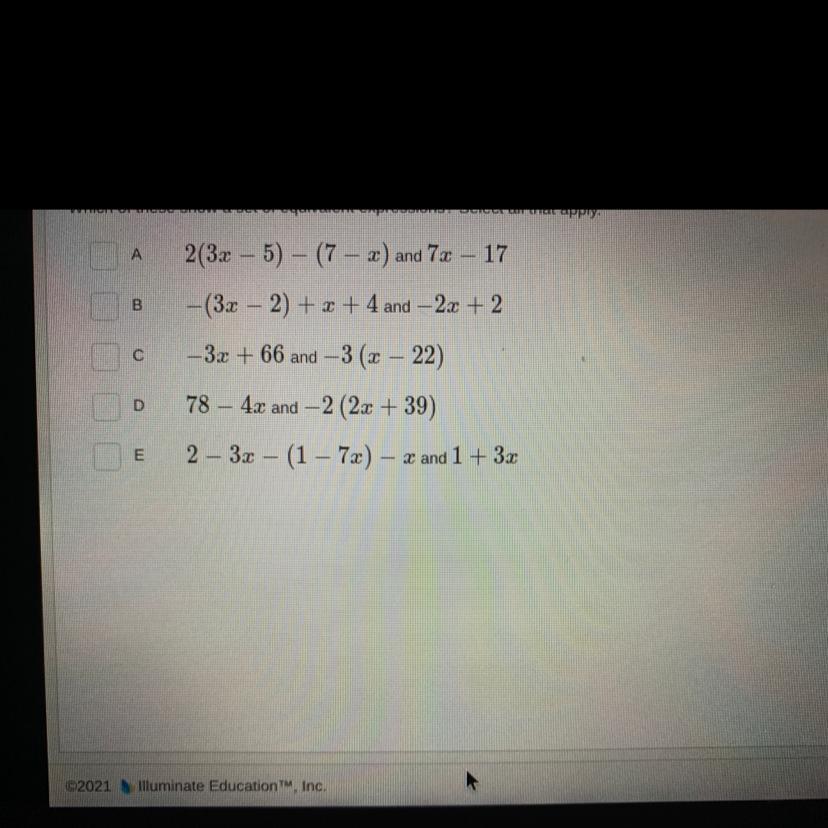
Answers
See work you in photo below
Good luck

Water flows from a kitchen faucet with a proportional relationship between the amount of time (in minutes) and the number of gallons.
If a total of 0.5 gallon of water flows out of the tap after 0.2 minute, what is the constant of proportionality?
What is the constant of proportionality?
Write your answer as a decimal.
gallons of water per minute
Answers
Answer:
2.5 gallons per minuteStep-by-step explanation:
Proportional relationship is determined by the equation:
y = kx, where k is the coefficient of proportionalityWe have:
y = 0.5 and x = 0.2Substitute the values into above equation and solve for k:
0.5 = 0.2kk = 0.5/0.2k = 2.5Answer:
2.5
Step-by-step explanation:
Let,
Constant of proportionality = x
0.5 = 0.2 × x
0.5/0.2 = x
5/2 = x
2.5 = x
Hence,
Constant of proportionality is 2.5
graph each equation using the slope and y-intercrept
1. y = 3/5 - 3
2. y = - 2/3x - 2
Answers
Answer:
1. Slope = -3/5
Y-intercept = (0, -3)
2. Slope = -2/3
Y-intercept = (0, -2)
Lauren spent $12.72 on 8 apps for her new tablet. If each app costs the same amount, how much did Lauren spend on each one?
$0.59
Answers
pls help if you can asap!!!!

Answers
Answer: x= 6
Step-by-step explanation:
Since the shape is a parallelogram, the angles will either be equal to each other or add up to 180.
You can see they do not look the same so they add up to equal 180
12x + 3 +105 = 180
12x + 108 = 180
12x = 72
x = 6
Which expression is equivalent to −4.6+(−0.4)+(−7.2) ? (4.6+0.4+7.2) −4.6−(0.4+7.2) (4.6+0.4)+(−7.2) −(4.6−0.4)+(−7.2)
Answers
Answer:
−4.6+(−0.4)+(−7.2) =−4.6−(0.4+7.2)
Step-by-step explanation:
Perfect Pizza has 15 toppings listed on their menu. How many ways could a customer choose a pizza that contains 3 different toppings?
Answers
If adding only twelve, you must leave out three of the fifteen, and the number of ways is = 15! / (3! * 12!).
1∗2∗3∗4∗5∗6∗6∗8∗9∗10∗11∗12∗13∗14∗15 over
(1∗2∗3)∗(1∗2∗3∗4∗5∗6∗6∗8∗9∗10∗11∗12) =
13∗14∗15 over
(1∗2∗3)
27306 = 455
Answer: If all toppings are distinct, then you have C 4 15 combinations. If there are three distinct toppings, you have 3 ⋅ C 3 15 combinations (because we have C 3 15 choices for toppings and then 3 choices for which of those three toppings is doubled).
Step-by-step explanation:
Can you help me with this

Answers
The rate at which Macros is pumping gas into his car is 1/6 gallons per second, which simplifies to 1 gallons per second. The correct answer is a. 1 gallons per second.
What is slope?The slope of the line is equal to the change in y-values (gallons of gas in car) divided by the change in x-values (seconds spent pumping gas).
To calculate the rate at which Macro is pumping gas into his car, we need to determine the slope of the line represented by the table values.
We can calculate the slope by subtracting the y-values for the first two points
(3 - 5 = -2)
and the x-values for the first two points
(0 - 12 = -12).
The slope is then equal to -2/-12 = 1/6.
Since the slope represents the rate of change, the rate at which Macro is pumping gas into his car is 1/6 gallon per second. This means that for every second he pumps gas into his car, he will add 1/6 gallon of gas.
This means that for every 6 seconds Macros pumps, he increases the amount of gas in his car by 1 gallon. Thus, the rate at which Macros is pumping gas into his car is 1/6 gallons per second, which simplifies to 1 gallons per second.
For more questions related to rate
https://brainly.com/question/25184007
#SPJ1
Find the surface area of the square pyramid. Next, find the area of the square base. Area of the 4 triangles: 280 cm² Area of the square: [?] cm² 10 cm 14 cm 10 cm

Answers
Answer:
Area of the square base = 100cm²
Surface area of square pyramid= 380cm²
Step-by-step explanation:
Area of the square base= L × L
= 10cm × 10cm
= 100cm²
The surface area of square pyramid= Area of the base + Area of the triangles forming the pyramid.
= 100cm² + 280cm²
What is the leading coefficient? - 3x3 + 8x2 + 9x - 4
A.
-4
B.
-3x3
C.
-3
D.
3
If you answer this I'll give you brainliest
Answers
Answer:
c
Step-by-step explanation:
the highest exponent is 3 so the leading coefficient is -3
Find X in circle below

Answers
Answer:
This is quite tough
it's hard
The length of each side of equilateral triangle T is 6 times the length of each side of equilateral triangle X.
Quantity A The ratio of the length of one side of T to
the length of another side of
Quantity B The ratio of the length of one side of X to
the length of another side of X
•A. Quantity A is greater.
• B. Quantity B is greater.
C. The two quantities are equal.
• D. The relationship cannot be determined from the information given.
Answers
C. The two quantities are equal. We can see that both Quantity A and Quantity B have the same value of 1. Hence, the two quantities are equal.
Since we know that the length of each side of triangle T is 6 times the length of each side of triangle X, we can set up the following equations:
Length of side of T = 6 * Length of side of X
To compare the ratios of the sides, we can use the following formula:
Ratio of one side to another = Length of one side / Length of another side
For Quantity A, we can choose any two sides of triangle T and find their ratio. Let's choose the two adjacent sides:
To further explain the concept, let's consider the properties of equilateral triangles.
An equilateral triangle is a special type of triangle where all three sides are equal in length. Hence, if we know the length of one side, we automatically know the length of all three sides.
Now, coming back to the given question, we are told that the length of each side of triangle T is 6 times the length of each side of triangle X. This means that if the length of one side of triangle X is 'a', then the length of one side of triangle T is 6 times 'a', which is '6a'.
Hence, we can write:
Length of side of T = 6a
Length of side of X = a
Now, let's compare the ratios of the sides.
For Quantity A, we need to find the ratio of one side of triangle T to another side of T. Let's choose the two adjacent sides:
Ratio of adjacent sides of T = Length of side of T / Length of adjacent side of T
Since all three sides of an equilateral triangle are equal, the adjacent side of T is also 6a. Hence, we get:
Ratio of adjacent sides of T = (6a) / (6a) = 1
For Quantity B, we need to find the ratio of one side of triangle X to another side of X. Let's again choose the two adjacent sides:
Ratio of adjacent sides of X = Length of side of X / Length of adjacent side of X
Since all three sides of an equilateral triangle are equal, the adjacent side of X is also 'a'.
To know more about quantities visit :-
https://brainly.com/question/14581760
#SPJ11