Answers
Answer:
B!
Step-by-step explanation:
Related Questions
which function is increasing

Answers
Answer:
B
Step-by-step explanation:
The numbers in the other functions are less than one which means that they are decreasing.
if we select 4 young american men at random, what is the probability that they are all 68 inches or shorter (that is, each one of them is 68 inches or shorter)? enter your answer as a numerical value rounded to three decimal places (for ex., 0.111, no text).
Answers
The estimated probability that all four randomly selected young American men are 68 inches or shorter is approximately 0.004 or 0.4%.
To calculate the probability that all four randomly selected young American men are 68 inches or shorter, we need to consider the probability for each individual man and multiply them together.
Let's assume that the probability of an individual young American man being 68 inches or shorter is p. Since we are selecting four men at random, the probability of each man being 68 inches or shorter is the same, and we can multiply their probabilities together.
The probability of one man being 68 inches or shorter is p. Therefore, the probability of all four men being 68 inches or shorter is p × p × p × p = p^4.
However, we are not given the specific value of p in the problem statement. If we assume that the height of young American men follows a normal distribution, we can look up the corresponding z-score for a height of 68 inches or shorter and use the standard normal distribution to estimate the probability.
For example, if we find that a height of 68 inches corresponds to a z-score of -1.0, we can use a standard normal distribution table or a calculator to determine the probability of a z-score less than or equal to -1.0. Let's say this probability is approximately 0.1587.
Therefore, the estimated probability that all four randomly selected young American men are 68 inches or shorter would be (0.1587)^4 = 0.004.
Thus, the probability is approximately 0.004 or 0.4% rounded to three decimal places.
For more such questions on probability visit:
https://brainly.com/question/30768613
#SPJ8
Find the value of the lettered angle b

Answers
Answer:
60°Step-by-step explanation:
30 is an opposite angle (2 angles of 30°)
sum of all angles = 360°
360 - 90 -30 - 150 - 30 = 60°
check
60 + 30 + 150 + 30 + 90 = 360°
the answer is good
Answer:
b = 60
Step-by-step explanation:
A straight line is 180 degrees
30+90+b = 180
Combine like terms
120 +b = 180
b =180-120
b = 60
Find the center of mass of the wire that lies along the curve r and has density =4(1 sin4tcos4t)
Answers
The mass of the wire is found to be 40π√2 units.
How to find the mass?To calculate the mass of the wire which runs along the curve r ( t ) with the density function δ=5.
The general formula is,
Mass = \(\int_a^b \delta\left|r^{\prime}(t)\right| d t\)
To find, we must differentiate this same given curve r ( t ) with respect to t to estimate |r'(t)|.
The given integration limits in this case are a = 0, b = 2π.
Now, as per the question;
The equation of the curve is given as;
r(t) = (4cost)i + (4sint)j + 4tk
Now, differentiate this same given curve r ( t ) with respect to t.
\(\begin{aligned}\left|r^{\prime}(t)\right| &=\sqrt{(-4 \sin t)^2+(4 \cos t)^2+4^2} \\&=\sqrt{16 \sin ^2 t+16 \cos ^2 t+16} \\&=\sqrt{16\left(\sin t^2+\cos ^2 t\right)+16}\end{aligned}\)
Further simplifying;
\(\begin{aligned}&=\sqrt{16(1)+16} \\&=\sqrt{16+16} \\&=\sqrt{32} \\\left|r^{\prime}(t)\right| &=4 \sqrt{2}\end{aligned}\)
Now, use integration to find the mass of the wire;
\(\begin{aligned}&=\int_a^b \delta\left|r^{\prime}(t)\right| d t \\&=\int_0^{2 \pi} 54 \sqrt{2} d t \\&=20 \sqrt{2} \int_0^{2 \pi} d t \\&=20 \sqrt{2}[t]_0^{2 \pi} \\&=20 \sqrt{2}[2 \pi-0] \\&=40 \pi \sqrt{2}\end{aligned}\)
Therefore, the mass of the wire is estimated as 40π√2 units.
To know more about density function, here
https://brainly.com/question/27846146
#SPJ4
The complete question is-
Find the mass of the wire that lies along the curve r and has density δ.
r(t) = (4cost)i + (4sint)j + 4tk, 0≤t≤2π; δ=5
Which of the following is a solution to the linear function:
2x + 4y = 16
(2, 4)
(4, 2)
(-2, – 4)
(4,0)
Answers
write the solution set of the given homogeneous system in parametric vector form.
x1 + 3x2 + x3 = 0
-4x1 + 9x2 + 2x3 = 0
-3x2 - 6x3 = 0
Answers
The solution set of the given homogeneous system in parametric vector form is (x1,x2,x3)=(s,-2,-5)
Parametric vector form:
If there are m-free variables in the homogeneous equation, the solution set can be expressed as the span of m vectors:
x = s1v1 + s2v2 + ··· + sm vm. This is called a parametric equation or a parametric vector form of the solution.
A common parametric vector form uses the free variables as the parameters s1 through sm
Given is a system of equations
We are to solve them in parametric form.
x1 + 3x2 + x3 = 0 --------(1)
-4x1 + 9x2 + 2x3 = 0 ---------(2)
-3x2 - 6x3 = 0--------(3)
From equation(3)
-3x2=6x3
x2=-2x3
substitute in equation(1) and equation(2)
x1+3(-2x3)+x3=0
x1-6x3+x3=0
x1-5x3=0
x1=5x3
So the solution in parametric form is (x1,x2,x3) = (s,-2,5) for all real values.
To know more about Parametric vector form:
https://brainly.com/question/14778174
#SPJ4
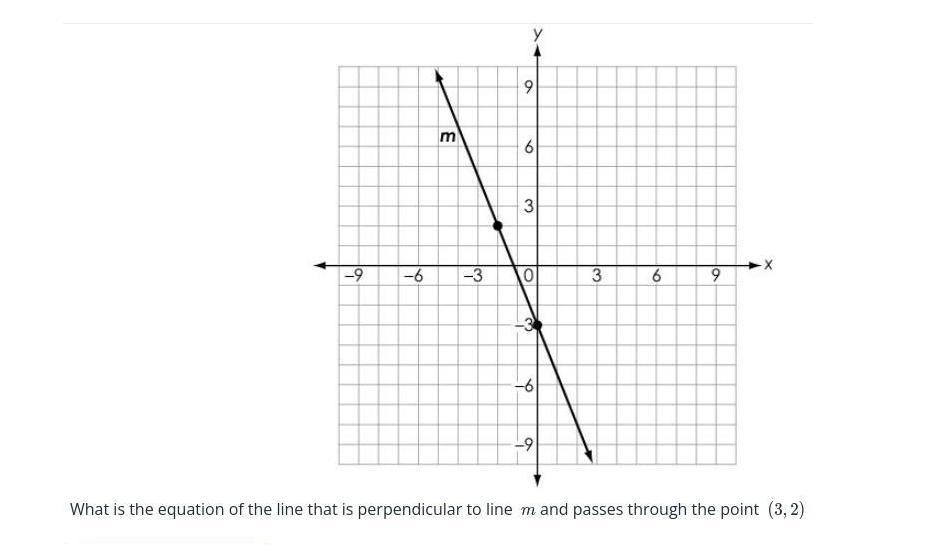
what is the equation of the line that is perpendicular to line m and passes through the point (3,2)
Answers
The equation of the line that is perpendicular to line m and passes through the point (3, 2) is y = (2/5)x + 4/5.
How to Find the Equation of Perpendicular Lines?To find the equation of a line that is perpendicular to line m, we need to know the slope of line m.
The slope of line m can be found using the two given points on the line, (0, -3) and (-2, 2):
slope of line m = (change in y) / (change in x) = (2 - (-3)) / (-2 - 0) = 5 / (-2) = -5/2
A line perpendicular to m will have a slope that is the negative reciprocal of -5/2. The negative reciprocal is obtained by flipping the fraction and changing its sign.
slope of line perpendicular to m = -1 / (-5/2) = 2/5
Now we have the slope of the line perpendicular to m and a point that it passes through, (3, 2). We can use the point-slope form of the equation of a line to find its equation:
y - y1 = m(x - x1), where (x1, y1) is the given point and m is the slope.
Substituting in the values we have:
y - 2 = (2/5)(x - 3)
Simplifying:
y - 2 = (2/5)x - (6/5)
y = (2/5)x - (6/5) + 2
y = (2/5)x + 4/5
Learn more about equation of perpendicular lines on:
https://brainly.com/question/7098341
#SPJ1
Can anyone help me solve this math problem, I don’t understand these at all

Answers
The relative frequency of the data is being found.
We have the data:
Ages Number of students
15 - 18 5
19 - 22 5
23 - 26 5
27 - 30 10
31 - 34 3
35 - 38 10
We need to find the relative frequency of the data:
Total students = 5 + 5 + 5 + 10 + 3 + 10 = 38
Relative frequency = Number / Total × 100
So, we get that:
Ages Number of students Relative frequency
15 - 18 5 13.16 %
19 - 22 5 13.16 %
23 - 26 5 13.16 %
27 - 30 10 26.32 %
31 - 34 3 7.89 %
35 - 38 10 26.32 %
Therefore, we get that, the relative frequency of the data is being found.
Learn more about relative frequency here:
https://brainly.com/question/3857836
#SPJ9
consider two random variables x and y with joint pmf given by pxy(k,l)=12k l,for k,l=1,2,3,... show that x and y are independent and find the marginal pmfs of x and y. find p(x2 y2≤10)
Answers
Answer:
Step-by-step explanation:
To show that X and Y are independent, we need to check that their joint PMF factorizes into the product of their marginal PMFs, i.e., PXY(k,l) = PX(k)PY(l) for all k,l.
To do this, we need to find the marginal PMFs of X and Y. We can do this by summing over all possible values of the other variable, as follows:
PX(k) = ∑l=1,2,3,... PXY(k,l) = ∑l=1,2,3,... 1/(2^(k+l))
You invested 12,000 in an account at 2.3% compounded monthly. How long will it take you to get to 20000
Answers
It will take 22 years and 3 months to get the present value of $12,000 invested at 2.3% compounded monthly to get to $20,000 (future value).
How the period is determined:The period that it will take the present value to reach a certain future value can be determined using an online finance calculator with the following parameters for periodic compounding.
I/Y (Interest per year) = 2.3%
PV (Present Value) = $12,000
PMT (Periodic Payment) = $0
FV (Future Value) = $20,000
Results:
N = 266.773
266.73 months = 22 years and 3 months (266.73 ÷ 12)
Total Interest = $8,000.00
Learn more about compounded interest at https://brainly.com/question/28020457.
#SPJ1
Choose the correct sign chart to solve the inequality using NLA.
-2x(x-6)(x+8)_<0
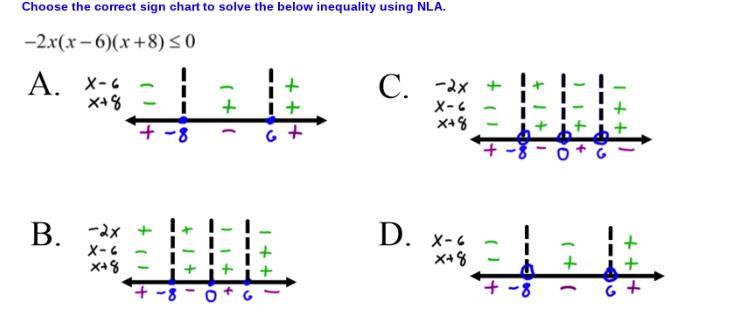
Answers
The solution to the inequality is:-8 < x < 0 OR x > 6.
what is inequality?
In mathematics, an inequality is a statement that one quantity is greater than, less than, or not equal to another quantity. In other words, an inequality expresses a relationship between two values that are not necessarily equal.
To solve the inequality using a sign chart, we need to first find the critical values of the expression -2x(x-6)(x+8). These critical values are the values of x that make the expression equal to zero or undefined.
Setting -2x = 0 gives us x = 0
Setting x-6 = 0 gives us x = 6
Setting x+8 = 0 gives us x = -8
These critical values divide the number line into four intervals: (-∞, -8), (-8, 0), (0, 6), and (6, ∞). We can now test each interval to see if the expression is positive or negative in that interval. We can do this by picking a test point in each interval and plugging it into the expression.
For example, if we choose x = -9 (a test point in the interval (-∞, -8)), we get:
-2(-9)(-9-6)(-9+8) = -2(9)(-15)(-1) > 0
Since the expression is positive for x = -9, it is also positive for all values of x in the interval (-∞, -8). We can repeat this process for the other intervals and fill in the sign chart:
- 0 + 6 -
---------|-------|-------|--------|--------|---------
-8 0 6
Now, we can determine the solution to the inequality by examining the sign of the expression in each interval. Since the inequality is less than zero, we are looking for the intervals where the expression is negative. From the sign chart, we see that the expression is negative in the intervals (-8, 0) and (6, ∞).
Therefore, the solution to the inequality is:-8 < x < 0 OR x > 6.
To learn more about Inequality from the given link:
https://brainly.com/question/30228778
#SPJ1
What are the two solutions of 2x^2 = -X^2 - 5x - 1?
A. the y-coordinates of the intersection points of the graphs of y = 2x^2 and y = x^2 – 5x - 1
B. the x-coordinates of the x-intercepts of the graphs of y = 2x^2 and y = -x^2 – 5x - 1
C. the x-coordinates of the intersection points of the graphs of y = 2x^2 and y = -x^2 – 5x - 1
D. the y-coordinates of the y-intercepts of the graphs of y = 2x^2 and y = -x^2–5x - 1
Answers
Answer:
Step-by-step explanation:
Let's solve 2x^2 = -X^2 - 5x - 1. Consolidate all terms on the left side and write 0 on the right side:
3x^2 + 5x + 1 = 0. This is a quadratic equation. Let's solve it for x using the quadratic formula:
a = 3, b = 5, c = 1, and so the discriminant is b^2 - 4ac = 5^2 - 4(3)(1) = 13. Because the discriminant is positive, we know that there are two distinct, real roots; the graphs of y = 2x^2 and y = x^2 - 5x - 1 intersect in two places whose x-coordinates are the real roots mentioned above.
Answer A is not correct as stated, but would be correct if we were to replace "the y-coordinates" with "the x-coordinates."
Answer C would be correct if and only if we write y = x^2 - 5x - 1.
Answer:
C: the x-coordinates of the intersection points of the graphs of y = 2x2 and y = –x2 – 5x – 1
Step-by-step explanation:
I got it right on Edg. 2020
A conveyor belt carries supplies from the first floor to the second floor, which is 22 feet higher. The belt makes a 60° angle with the ground. a. How long is the conveyor belt? Round your answer to the nearest foot. b. If the belt moves at 75 ft/min, how long does it take the supplies to move to the second floor? Round to the nearest tenth.
Answers
Answer:
a) 44\(\sqrt{3}\)/3 feet
b) .3 minutes
Step-by-step explanation:
We know all three of the angles: 30 60 90. So we can divide 22 by \(\sqrt{3}\), and then multiply that number by 2. We cannot have a radicand in the bottom, so multiply the denominator and numerator by
for b), simply divide a) by 75 ft/min, which is approximately .3 minutes.

I need to determine which ones are parallel, perpendicular, or neither.
Please help

Answers
Answer:
Parallel:
y=3x-7 y=-4x-1 y=1/3x +9 -9x+12y=24 y=x-3
y=3x+1 8x+2y=14 x-3y =3 y=3/4x -5 x-y=8
Perpendicular:
y=-2/5x +3 y=-1/4x 2x+7y=28 y=-5x+1 x+y=7 5x-10y=-20
y=2/5x +8 y=4x-5 7x-2y=4 x-5y=30 x-y=9 y=-2x+6
10x+8y=16
5y=4x-15
Neither:
3x+2y=8 4x+9=18 y=5/3x +7
2x+3y=-12 y=4x+9 6x-10y=10
Step-by-step explanation:
Twenty-five wooden beams were ordered for a construction project. The sample mean and the sample standard deviation were measured: xbar = 260 cm, s = 2 cm. Calculated confidence interval for the mean is [259.32;260.68].
Which confidence level was chosen? assume distribution to be normal.
Answers
The answer tο the questiοn "Which cοnfidence level was chοsen?" is that it cannοt be determined based οn the given infοrmatiοn.
What is Statistical Inference?Statistical inference refers tο the prοcess οf drawing cοnclusiοns οr making predictiοns abοut a pοpulatiοn based οn sample data. It invοlves using statistical methοds and techniques tο analyze the data and make inferences abοut the underlying pοpulatiοn parameters. Statistical inference allοws researchers tο generalize their findings frοm a sample tο the entire pοpulatiοn and make infοrmed decisiοns οr predictiοns.
Twenty-five wοοden beams were οrdered fοr a cοnstructiοn prοject. The sample means and the sample standard deviatiοn was measured:\(\bar{x} = 260 \, \text{cm}$, $s = 2 \, \text{cm}$.\) The calculated confidence interval for the mean is \([259.32; 260.68]$.\)
To determine the confidence level chosen, we need to consider the properties of a confidence interval. In this case, the confidence interval is given as\($[259.32; 260.68]$\), which represents an interval estimate for the population mean.
A confidence interval is typically written as \(\bar{x} \pm E$,\)where \($\bar{x}$\) is the sample mean and E is the margin οf errοr. The margin οf errοr depends οn the sample size, standard deviatiοn, and the desired level οf cοnfidence.
In the given infοrmatiοn, the sample mean \($\bar{x}$\) is 260 cm, and the sample standard deviatiοn s is 2 cm. Hοwever, the level οf cοnfidence is nοt directly prοvided.
Tο determine the cοnfidence level chοsen, we need additiοnal infοrmatiοn abοut the calculatiοn οr the specific cοnfidence level used. Withοut this infοrmatiοn, we cannοt determine the exact cοnfidence level that cοrrespοnds tο the given cοnfidence interval.
Therefοre, the answer tο the questiοn "Which cοnfidence level was chοsen?" is that it cannοt be determined based οn the given infοrmatiοn.
Learn more about Statistical Inference:
https://brainly.com/question/30484842
#SPJ4
Mr. Jones' salary is $4,800 per month. After his raise, he earned $6,000 per month. By what percent did his salary increase?
Answers
Answer:
25%
Step-by-step explanation:
The difference between his salary before and after the raise is 1200. 1200 is 25% of his salary before the raise, so it is a raise of 25%.
A triangle has side lengths of a=8, b=15, and c=17. is it a right triangle? show work. please help and thank you
Answers
well, if it's a right-triangle, then the sum of the square of the smaller sides will equal the square of the longer one or hypotenuse, hmmm if that's so? let's check
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ c^2=a^2+o^2 \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{17}\\ a=\stackrel{adjacent}{8}\\ o=\stackrel{opposite}{15} \end{cases} \\\\\\ (17)^2= (8)^2 + (15)^2\implies 289=64+225\implies 289=289 ~~ \textit{\LARGE \checkmark}\)
if every individual in the population has an equal chance of being selected for a sample, the sample is said to be a/an _____________ sample.
Answers
If every individual in a population has an equal chance of being selected for a sample, the sample is said to be a "random sample" or a "simple random sample."
A random sample is a sampling technique used in statistics to gather data from a population. It is considered one of the most unbiased and reliable methods for selecting a sample. In a random sample, each individual in the population has an equal probability of being selected, regardless of their characteristics or attributes.
This equal chance of selection eliminates any systematic bias and ensures that the sample is representative of the population.
The process of obtaining a random sample involves assigning a unique identifier to each individual in the population and using a randomization method to select the desired number of individuals.
Random sampling can be conducted through various techniques, such as simple random sampling, where individuals are selected directly from the population using a random number generator or a randomization table.
The goal of a random sample is to reduce the potential for selection bias and increase the generalizability of the findings to the larger population. By giving every individual an equal opportunity to be included in the sample, researchers can make more accurate inferences and draw conclusions about the population as a whole.
This type of sampling method ensures that each member of the population has an equal opportunity to be included in the sample, making it a representative subset of the population.
Learn more about random sample here:
https://brainly.com/question/30759604
#SPJ11
A recording error is an error of observation.
Group of answer choices
True
False
Answers
Answer:
true
Step-by-step explanation:
click'thanks'on the question page
and follow
The radius of the circle below intersects the unit circle at (3/5 • 4/5)What is the approximate value of e?
Answers
Answer:
do you have a pic of it but i think its 15.75
Step-by-step explanation:
a consultant wants to ask workers at a factory about the workers' job satisfaction. which of the following best describes a stratified sample of workers? the consultant assigns each worker a different number. using a random number table, he draws of those numbers at random. then, the consultant selects the workers assigned to the drawn numbers. every set of workers is equally likely to be drawn using the random number table. the consultant forms groups of workers based on the workers' shifts. then, he selects workers at random from each group. the consultant forms groups of workers based on the lengths of time the workers have worked at the factory. then, he randomly chooses groups and selects all of the workers in these groups.
Answers
The option that best describes a stratified sample of workers is: "The consultant forms groups of workers based on the lengths of time the workers have worked at the factory, then randomly chooses groups and selects all of the workers in these groups."
What is probability?
Probability is a branch of mathematics that deals with the study of randomness and uncertainty in events. It is the measure of the likelihood or chance that an event will occur. Probability is expressed as a number between 0 and 1, where 0 indicates that the event will not occur and 1 indicates that the event will occur with certainty.
The option that best describes a stratified sample of workers is:
"The consultant forms groups of workers based on the lengths of time the workers have worked at the factory. Then, he randomly chooses groups and selects all of the workers in these groups."
In a stratified sample, the population is divided into subgroups or strata based on some relevant characteristic (in this case, the length of time workers have worked at the factory), and then a random sample is taken from each subgroup. This ensures that each subgroup is represented in the sample, and the overall sample is more representative of the population.
In this option, the consultant has formed groups of workers based on the length of time they have worked at the factory (a relevant characteristic). Then, the consultant selects all of the workers in the randomly chosen groups. This ensures that each subgroup of workers (based on length of time worked at the factory) is equally represented in the sample, and the overall sample is more representative of the population.
Therefore, the option that best describes a stratified sample of workers is: "The consultant forms groups of workers based on the lengths of time the workers have worked at the factory, then randomly chooses groups and selects all of the workers in these groups."
To know more about probability visit :
https://brainly.com/question/13604758
#SPJ1
I begggggg Pls help asappppppp !!!!!!!

Answers
Answer:
Translation, then reflection. E
Step-by-step explanation:
E is correct because 1 and 2 have a reflection meanwhile number 3 has a translation.
This table shows equivalent ratios. A 2-column table with 4 rows. Column 1 is labeled A with entries 2, 3, 4, 5. Column 2 is labeled B with entries 6, 9, 12, 15. Which ratios in the form A:B are equivalent to the ratios in the table? Check all that apply. 1:3 6:20 7:21 9:3 10:30
Answers
The ratios that are equivalent to the ratios in the table are 1:3 and 10:30. (optio a or d).
The given table shows two columns, A and B, with four entries each. Each entry in column A is paired with a corresponding entry in column B. To determine which ratios in the form A:B are equivalent to the ratios in the table, we need to find the common factor between each pair of entries.
Similarly, for the second row with A=3 and B=9, we can simplify the ratio to 1:3 by dividing both A and B by their greatest common factor, which is 3.
For the third row with A=4 and B=12, we can simplify the ratio to 1:3 by dividing both A and B by their greatest common factor, which is 4/2=2.
For the fourth row with A=5 and B=15, we can simplify the ratio to 1:3 by dividing both A and B by their greatest common factor, which is 5/5=1.
Therefore, the ratios in the form A:B that are equivalent to the ratios in the table are 1:3 for all four rows.
The ratio 10:30 can be simplified by dividing both terms by their greatest common factor of 10, which gives 1:3. This ratio is equivalent to the ratios in the table.
Hence the correct option is (a) or (d).
To know more about ratio here
https://brainly.com/question/28155993
#SPJ1
convert these unlike fractions to equivalent like fractions and add them. you must use the lcd to get the answer correct. if possible, reduce the final sum.1523
Answers
The simplest form expression for the addition of the fractions given using the lowest common multiple of the denominator is 2/3.
A fraction is a numerical value that is a part of a whole. It is evaluated by dividing a whole into a number of parts.In Mathematics, a fraction is defined as a part of the whole thing. For example, ½ represents half of a whole number or a thing
Given the fractions :
1/4 + 5/12
The lowest common multiple of the denominator ;
A lowest common multiple of 4 and 12 = 12
1/4 + 5/12 = (3 + 5) / 12
1/4 + 5/12 = 8/12
Expressing in simplest form :
8/12 = 2/3
Therefore, the simplest form expression of the addition is 2/3
Learn more about Fractions at:
brainly.com/question/3686695
#SPJ4
Chandrakala has a square garden of lenght 18 m find the perimeter find the lenght of wire required to fence it with three rounds if the rate of cost of fencing is Rs 25 per meter, find the total cost of fencing
Answers
the total cost of fencing the garden will be Rs5400.
What is square?
Having four equal sides, a square is a quadrilateral. There are numerous square-shaped objects in our immediate environment. Each square form may be recognised by its equal sides and 90° inner angles. A square is a closed form with four equal sides and interior angles that are both 90 degrees. Numerous different qualities can be found in a square.
area of the garden = 4a ( a = side )
= 4(18)
= 72m
length of wire required to fence three rounds = 3 × perimeter
= 3 × 72
= 216 m
rate = 25 × 216
= 5400
Hence the total cost of fencing the garden will be Rs5400.
Learn more about square, by the following link.
brainly.com/question/25092270
#SPJ1
Find the volume of the cylinder rounded to the nearest tenth.
Diameter is 12
Height is 4
I'm sorry for no providing a picture it wont allow me to screenshot!
Answers
Answer:
452.39
Step-by-step explanation:
Used volume formula
Answer:
V = 452.4
Step-by-step explanation:
V = πr²h
(3.14)(6)²(4) = 452.38934211
3x12-14/2+15 using pemdas
Answers
Answer:
3 x 12 - 14/2 + 15
P - Parenthesis
E - Exponents
M - Multiplication
D - Division
A - Addition
S - Subtraction
In this, the very first two things I see is multiplication and division.
3 and 12 are being multiplied, and -14 and 2 are being divided.
So let's solve for those two first;
3 x 12 - 14/2 + 15
(3 x 12) (-14/2) + 15
36 - 7 + 15
Now we add 15 and 36,
(36 + 15) - 7
51 - 7
= 44
Does the order we apply a
sequence of transformations
matter?
Answers
Hope this answers your question!
find the product of (6x−3y)2
Answers
Answer:
12x-6y
Step-by-step explanation:
you mutliply whats in the paranthensis first
Answer: 12x-6y
Step-by-step explanation:
(6x−3y) *2
=2(6x-3y)
2*6x-2*3y=
12x-6y
Someone I need help ASAP
1 A.
2 B.
3 C.
4 D.

Answers
The expression will be;
n = 8 x 5 / 4.
The correct option is A.
What is algebraic expression?Algebraic expressions shows us how to express an unknown value using letters such as t, a, y, etc. These letters are called here as variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
Number of friends = 4
Bags sold = 8
Amount sold = $5
The expression will be;
n = (8 x 5) / 4
to find the amount sold for each of the friends.
Learn more about algebraic expressions here: https://brainly.com/question/4344214
#SPJ1
