Answers
In simple interest, we can use the formula:
\(I=P\cdot r\cdot t\)Where P is the principal value, that is, the value of the loan, $9000; r is the annual rate and t is the period of loan in years.
We know Rita paid interest of $336, so
\(I=336\)However, the period that she had is not in years, it is in months. However, in simple interest we can just convert "t" from year to months. If she got 7 months, this is equivalent of 7/12 years, because one year has 12 months.
Thus, t = 7/12
Now, we know "I", "P" and "t", we can substitute and solve for "r":
\(\begin{gathered} 336=9000\cdot r\cdot\frac{7}{12} \\ \frac{336}{9000}=r\cdot\frac{7}{12} \\ 0.037333\ldots=r\cdot\frac{7}{12} \\ r=\frac{12}{7}\cdot0.037333\ldots \\ r=\frac{0.448}{7}=0.064 \end{gathered}\)In percentage, we have 6.4% of annual interest.
Related Questions
Question 4
This Test: 24 pts possible
Enter your search term
The exercise statement and the correct answer is given. Select the correct directions from "Find the
opposite," "Find the reciprocal," or "Evaluate or simplify."
- 16
Answer: 16
...
Choose the correct answer below.
O A. Find the reciprocal.
OB. Find the opposite.
O C. Evaluate or simplify.
Answers
Answer:
Reciprocal is -1/16
opposite is +16 or 16
so answer is 16 is opposite of -16
Evaluate and simplify the following complex fraction.

Answers
Answer:
The answer is
\( - \frac{10}{7} \: \: \: or \: \: - 1 \frac{3}{7} \)Step-by-step explanation:
\( \frac{ - \frac{5}{7} }{ \frac{2}{4} } \)First of all we can write the fraction as
\( - \frac{5}{7} \div \frac{2}{4} \)Simplify the second fraction
That's
\( \frac{2}{4} = \frac{1}{2} \)So we have
\( - \frac{5}{7} \div \frac{1}{2} \)Next change the division sign to multiplication sign and reverse the second fraction
That's
\( -\frac{5}{7} \times \frac{2}{1} \)Multiply the terms
We have the final answer as
\( - \frac{10}{7} \: \: \: or \: \: - 1 \frac{3}{7} \)Hope this helps you
2x+5=10
someone help me
Answers
Answer:
2x=5 x=2.5
Step-by-step explanation:
2x+5=10
2x=10-5
2x=5
x=2.5
Answer:
yes the answer is 10
Step-by-step explanation:
Given ABC below, with m C = 115°, a = 6, and b = 8, find the area of the triangle. Round your answer to the nearest tenth and do not include units in your answer.

Answers
ANSWER
Area = 21.8
EXPLANATION
Looking at the given triangle closely, you will notice it's a Non-Right Triangle.
Now, to find the area of Non-Right Triangle, we make use of the formula below:
\(\text{Area = }\frac{1}{2}ab\text{ sin C}\)From the question,
Which shows the result of a correct substitution for the system y=2x+3 and 3x+2y=9?
Answers
Answer:
The result of the correct substitution gives:
x = 3/7 and y = 27/7
Step-by-step explanation:
From the given information:
y = 2x + 3 ---- (1)
3x + 2y = 9 ---- (2)
By using substitutional method
Substitute the value of y = 2x +3 into equation (2)
So,
3x + 2(2x + 3) = 9
3x + 4x + 6 = 9
7x = 9 - 6
7x = 3
x = 3/7
From equation (1), let replace the value of x to be 3/7
So,
y = 2x + 3
y = 2(3/7) + 3
y = 6/7 + 3
y = 27/7
How many three-digit numbers can be formed under each condition?
(a) The leading digit cannot be zero.
(b) The leading digit cannot be zero and no repetition of digits is allowed.
(c) The leading digit cannot be zero and the number must be a multiple of 3.
(d) The number is at least 400.
Answers
Answer:
I think A is the right answer
Madison needs to buy enough meat to make 1,000 hamburgers for the company picnic. Each hamburger will weigh 0.25 pound. How many pounds of hamburger meat should Madison buy?
Answers
Answer:
Madison needs to buy 250 pound of meat
Step-by-step explanation:
please I need help on question 6

Answers
The value of the variable x and the measures of each side of the triangle ΔDEF found using the definition of an isosceles triangle are;
x = 9
DE = 13
EF = 28
DF = 28
What is an isosceles triangle?An isosceles triangle is a triangle that has two angles in the triangle that are congruent and two congruent sides.
The specified parameters are;
∠D is congruent to ∠E in triangle ΔDEF
The length of the segments of ΔDEF are;
DE = x + 4
EF = 4·x - 8
DF = 7·x - 35
The (base) angles ∠D and ∠F of ΔDEF are congruent, therefore, ΔDEF is an isosceles triangle (definition)
Therefore;
EF = DF (Definition of an isosceles triangle)
4·x - 8 = 7·x - 35
7·x - 4·x = 3·x = 35 - 8 = 27
3·x = 27
x = 27 ÷ 3 = 9
x = 9
DE = x + 4
Therefore;
DE = 9 + 4 = 13
EF = 4·x - 8
Therefore;
EF = 4 × 9 - 8 = 28
DF = 7·x - 35
Therefore;
DF = 7 × 9 - 35 = 28
Learn more about isosceles triangles in geometry here:
https://brainly.com/question/29618252
#SPJ1
NEED HELP!! I"LL GIVE YOU BRAINLIEST!! Find the value of b. a = 3 and c =12

Answers
Answer: b = 11.62
Step-by-step explanation:
We can use this formula to solve for b:
\(b^{2} =\) \(\sqrt{c^{2}-a^{2} }\)
\(b^{2} =\) \(\sqrt{12^{2}-3^2 }\)
\(b^2= \sqrt{144-9}\)
= 11.61895004
We can round that to 11.62.
Hope this helped!
point is randomly chosen on the grid shown below.
What is the likelihood that the point is in the blue section of the grid?
It is certain
O It is impossible.
It is likely
It is unlikely.

Answers
Answer:
It is Unlikely.
Step-by-step explanation: The grid is 5x4 which is 20 total squares with 6 blue squares inside. The possibilty of landing in the blue area is 6/20, which is less than 10/20, or equally likely. Because the possibilty is less than 50 percent, the likihood of a point chosen in the blue section would be unlikely.
Answer:
it is unlikely
Step-by-step explanation:
got it right on edg 2020
The product is???
It is multiplication.
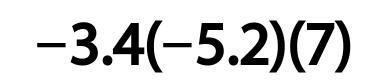
Answers
Answer:
answer is 123.76
window is 8 2/3 feet wide and 5 3/4 what is the area of the window
Answers
Sophie answered 84% of the questions on her science test correctly. If she answered 21 questions correctly, how many questions were on the test?
Answers
Answer:25
Step-by-step explanation:
An airplane can travel 350 mph in still air. If it travels 1995 miles with the wind
in the same length of time it travels 1505 miles against the wind, what is the speed of the wind?
Answers
Answer:
49 mph
Step-by-step explanation:
RT=D
T = D/R
\(\frac{1995}{(350 + x) } =\frac{1505}{350-x}\)
1995(350-x) = 1505(350+x)
x=49
Choose the expression that correctly compares the numbers 117 and 171.
171 < 117
171 = 117
171 > 117
117 > 171
Answers
Answer:
171 > 117
Step-by-step explanation:
171 is greater than 117 meaning the alligator is eating the bigger number, 171.
The function
f(x) = 5sqrt(x + 13) + 5 has an inverse f ^ - 1 * (x) defined on the domain x < 5 Find the inverse. x >= - 13
Answers
The inverse function: \(f^{-1} (x) =\) \((\frac{x -5}{5} )^{2} -13\)
The inverse is defined on the domain x < 5 and x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5.
What is a function?A function is a relationship that exists between two sets of numbers, with each input from the first set, known as the domain, corresponding to only one output from the second set, known as the range.
Given function is; \(f(x) = 5\sqrt{(x + 13)} + 5\)
To find the inverse of the given function, we first replace f(x) with y:
⇒ \(y = 5\sqrt{(x + 13)} + 5\)
Subtract 5 from both sides:
⇒ \(y -5 = 5\sqrt{(x + 13)}\)
⇒ \(\frac{(y -5)}{5} = \sqrt{(x + 13)}\)
⇒ \((\frac{y -5}{5} )^{2} = x + 13\)
⇒ \((\frac{y -5}{5} )^{2} -13 = x\)
Now we have x in terms of y, so we can replace x with f⁻¹(x) and y with x to get the inverse function:
f⁻¹(x) = \((\frac{x -5}{5} )^{2} -13\)
The domain of the inverse function is x ≥ 5, because this is the range of the original function, and we were given that the inverse is defined on the domain x < 5. However, we must also exclude the value x = 5, because the denominator of the fraction \((\frac{x -5}{5} )^{2}\) becomes zero at this value. Therefore, the domain of f⁻¹(x) is x > 5.
We were given that x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5. Therefore, the domain of the inverse function becomes the range of the original function, and the range of the inverse function becomes the domain of the original function.
To know more about domain, visit:
https://brainly.com/question/26098895
#SPJ1
What other pair of corresponding congruent parts is needed to prove that the two triangles are congruent by ASA congruence postulate?
Answers
By another pair of sides along with pair of angles we can prove that two triangles are congruent by ASA congruence postulate.
What is ASA Congruence Postulate?
A set of triangles can be proven to be congruent using the angle-side-angle rule.
According to the ASA rule, two triangles are congruent if their two included sides and two angles are the same as those of another triangle.
Using the ASA Congruence Postulate and by considering the following image,
∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other.
i.e. BC= QR.
Hence, Δ ABC ≅ Δ PQR.
Therefore, By another pair of sides along with pair of angles we can prove that two triangles are congruent by ASA congruence postulate.
To know more about ASA congruence postulate visit,
https://brainly.com/question/3168048
#SPJ4

Triangle ABC has vertices at A(−3, 3), B(0, 7), and C(−3, 0). Determine the coordinates of the vertices for the image if the preimage is translated 3 units up.
A′(−3, 0), B′(0, 4), C′(−3, −3)
A′(−3, 6), B′(0, 10), C′(−3, 3)
A′(−6, 3), B′(−3, 7), C′(0, 0)
A′(0, 3), B′(3, 5), C′(0, 0)
Answers
Answer:
To translate triangle ABC 3 units up, we need to add 3 to the y-coordinate of each vertex:
A' = (-3, 3 + 3) = (-3, 6)
B' = (0, 7 + 3) = (0, 10)
C' = (-3, 0 + 3) = (-3, 3)
Therefore, the coordinates of the vertices for the image triangle A'B'C' are A'(-3, 6), B'(0, 10), and C'(-3, 3).
So the correct answer is: A′(−3, 6), B′(0, 10), C′(−3, 3).
Four friends go to dinner. Each chooses a different meal. When the check comes, they decide they will each pay the same amount. If the costs of the meals (including tax and tip) were $12.20, $11.00, $8.50, and $7.50, what should each friend pay so they cover the whole bill?
Answers
Answer: Each friend should pay $9.80
Step-by-step explanation: First add up all their checks, then divide them by 4 (4 because there 4 friends) to get the amount each friend needs to pay.
$12.20 + $11.00 + $8.50 + $7.50= $39.20
39.30 / 4 = $9.80
C
Carla has $25.00 to spend at the arcade.
. It costs $3.00 to get a playing card that you have to use to play the games
It costs $2.50 per game
. She also buys snacks and a drink for $6.50
What is the maximum number of games that she can play?
Answers
The ratio of boys to girls in the sixth grade was 5:7. If there are 14 more girls, how many sixth graders are there?
Answers
Answer:
84
Step-by-step explanation:
7-5=2
2u-> 14
1u->7
7+5=12
12u-> 84
Answer:
boy=5 girls=7 + 14= 21 girls
Step-by-step explanation:
Please answer see the image please answer correctly, please

Answers
Step-by-step explanation:
not wrong that is super right
figure below represents a floor covered with white tiles and gray tiles. KEY = 1 square unit
Answers
According to the information, we can infer that the correct expression is (10 * 7) + (2 * 7) (option D).
How to find the correct expression?To find the correct expression we must look at the graph and interpret the information it has. In this case, some tiles are white and others are gray, so they would represent different elements. In this case, the white area is 10 * 7 tiles, so this would be the first part of the expression.
On the other hand, the second part of the expression would be 7 * 2, which represents the length, length and width of the gray area. According to the above, the correct expression would be (10 * 7) + (2 * 7), the first part in parentheses represents the white area and the second part in parentheses represents the gray area.
Learn more about tiles in: https://brainly.com/question/18257982
#SPJ1
Add The follwing pqr+3pqr
Answers
Answer:
4pqr
Step-by-step explanation:
because pqr is 1pqr
so 1pqr + 3pqr is
4pqr
If function f is a cubic polynomial which statement most accurately describes the function over the interval (0,1)

Answers
We have a cubic function f and we are asked to describe what happens in the interval from 0 to 1
If we look at the values of f for x=0 and x=1 it is going from -6 to 0 so the function is growing
in conclusion, the function is increasing over the interval (0,1)
Expand the function.
f(x) = (3x-4)4
81x4 − 432x³ + [? ]x²
+
-
X +
PLS HELP
Answers
The expansion of the function \((3x - 4)^4\) simplifies to \(81x^4 - 432x^3 + 864x^2 - 768x + 256.\)
To expand the function \(f(x) = (3x - 4)^4\), we can use the binomial theorem. According to the binomial theorem, for any real numbers a and b and a positive integer n, the expansion of \((a + b)^n\) can be written as:
\((a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^{(n-1)} b^1 + C(n, 2)a^{(n-2)} b^2 + ... + C(n, n-1)a^1 b^{(n-1)} + C(n, n)a^0 b^n\)
where C(n, k) represents the binomial coefficient, which is given by C(n, k) = n! / (k!(n-k)!).
Applying this formula to our function \(f(x) = (3x - 4)^4\), we have:
\(f(x) = C(4, 0)(3x)^4 (-4)^0 + C(4, 1)(3x)^3 (-4)^1 + C(4, 2)(3x)^2 (-4)^2 + C(4, 3)(3x)^1 (-4)^3 + C(4, 4)(3x)^0 (-4)^4\)
Simplifying each term, we get:
\(f(x) = 81x^4 + (-432x^3) + 864x^2 + (-768x) + 256\)
Therefore, the expanded form of the function \(f(x) = (3x - 4)^4\) is \(81x^4 - 432x^3 + 864x^2 - 768x + 256\).
Note that the coefficient of \(x^3\) is -432, the coefficient of \(x^2\) is 864, the coefficient of x is -768, and the constant term is 256.
For more question on function visit:
https://brainly.com/question/11624077
#SPJ8
Note the complete question is
![Expand the function.f(x) = (3x-4)481x4 432x + [? ]x+-X + PLS HELP](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/GfWbZg9TGTD1FI7gZnK9lbVdLBpjkw5X.jpeg)
If g(x) = 1 − x3, find g'(0)
Answers
Answer:
Step-by-step explanation:
we just have to substitute 0 in place of x
1-(0)³, 0³ is still 0, so we're left with 1-0=1
mark me brainliest of it helped
What is the answer pleaseee

Answers
Answer: 803.84cm3
Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.
To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.
4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.
Now, we have the area of the circle. 50.24cm squared!
The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,
16cm x 50.24cm squared = 803.84cm cubed.
The volume of the can of soup is 803.84cm cubed.
ASAP Please!
Beth purchased a $50,000 nonparticipating whole life insurance policy. The annual premium was $1,608. The cash value of the policy after 10 years will be $13,740. Assuming 5% interest rates. What is the traditional net cost of this policy, per thousand per year, over the first 10 years the policy is in force? (Round your answer to 2 decimal places)
Answers
Based on the annual premium, the cash value of the policy, and the number of years, the traditional net cost of this policy over the first 10 years is 5.76.
What is traditional net cost?First, find the net cost over 10 years:
= Total premium over 10 years - cash value
= (1,608 x 10) - 13,740
= $2,340
The net cost per year is:
= 2,340 / 10
= $234
The traditional net cost of this policy, per thousand per year for the first 10 years is:
= 234 / 50,000 x 1,000
= 4.68
Find out more on the cost of insurance policies at https://brainly.com/question/23282485
#SPJ1
The height h of an object thrown from the top of a ski lift 1240 feet high after t seconds is h=-16t2 +32t+1240. For what times is the height of the object at least 1000 feet?
←
The height of the object is at least 1000 feet from seconds to seconds.
Answers
Check the picture below.
so the parabolic path of the object is more or less like the one shown below in the picture, now this object has an initial of 1240 ft, as it gets thrown from the ski lift, so from 0 seconds is already higher than 1000 feet.
\(h=-16t^2+32t+1240\hspace{5em}\stackrel{\textit{a height of 1000 ft}}{1000=-16t^2+32t+1240} \\\\\\ 0=-16t^2+32t+240\implies 16t^2-32t-240=0\implies 16(t^2-2t-15)=0 \\\\\\ t^2-2t-15=0\implies (t-5)(t+3)=0\implies t= \begin{cases} ~~ 5 ~~ \textit{\LARGE \checkmark}\\ -3 ~~ \bigotimes \end{cases}\)
now, since the seconds can't be negative, thus the negative valid answer in this case is not applicable, so we can't use it.
So the object on its way down at some point it hit 1000 ft of height and then kept on going down, and when it was above those 1000 ft mark happened between 0 and 5 seconds.

