I need help sooo bad

The value of a(t) is -1 and b(t) is 55 + \(e^t\)

No, the given equation y' - y = 55 + \(e^t\) is not in the standard form of a first-order linear differential equation.

In the method for solving a first-order linear differential equation, an integrating factor is a function used to transform the equation into a form that can be easily solved.

For an equation in the standard form y' + a(t)y = b(t), the integrating factor is defined as:

μ(t) = e^∫a(t)dt

To solve the equation, you multiply both sides of the equation by the integrating factor μ(t) and then simplify. This multiplication helps to make the left side of the equation integrable and simplifies the process of finding the solution.

To put it in standard form, we need to rewrite it as y' + a(t)y = b(t).

Comparing the given equation with the standard form, we can identify:

a(t) = -1

b(t) = 55 + \(e^t\)

Therefore, The value of a(t) is -1 and b(t) is 55 + \(e^t\)

Learn more about integrating factor here

https://brainly.com/question/32554742

#SPJ4

Answer:

he actual densities of pure, dry, geologic materials vary from 880 kg/m3 for ice (and almost 0 kg/m3 for air) to over 8000 kg/m3 for some rare minerals. Rocks are generally between 1600 kg/m3 (sediments) and 3500 kg/m3 (gabbro).

Step-by-step explanation:

Answer:

is that a question

Step-by-step explanation:

d) Tthe probability that there is a moving object given that both sensors detect motion is approximately 0.98.

(a) To find the probability that sensor L detects motion given that there is movement outside and sensor V does not detect motion, we can use Bayes' theorem.

Let's denote the events as follows:

A = Movement outside

B = Sensor V does not detect motion

C = Sensor L detects motion

We are given:

P(A) = 0.7 (probability of movement outside)

P(B|A) = 0.05 (probability of sensor V not detecting motion given movement outside)

P(C|A) = 0.8 (probability of sensor L detecting motion given movement outside)

We want to find P(C|A', B), where A' denotes the complement of event A.

Using Bayes' theorem:

P(C|A', B) = [P(A' | C, B) * P(C | B)] / P(A' | B)

We can calculate the values required:

P(A' | C, B) = 1 - P(A | C, B) = 1 - P(A ∩ C | B) / P(C | B) = 1 - [P(A ∩ C ∩ B) / P(C | B)]

             = 1 - [P(B | A ∩ C) * P(A ∩ C) / P(C | B)]

             = 1 - [P(B | C) * P(A) * P(C | A) / P(C | B)]

             = 1 - [P(B | C) * P(A) * P(C | A) / [P(B | C) * P(A) * P(C | A) + P(B | C') * P(A') * P(C | A')]]

P(B | C) = 0 (since sensor V does not detect motion when there is motion outside)

P(C | A') = 0 (since sensor L does not detect motion when there is no motion outside)

Substituting these values:

P(C | A', B) = 1 - [0 * P(A) * P(C | A) / (0 * P(A) * P(C | A) + P(B | C') * P(A') * P(C | A'))]

             = 1 - [0 / (0 + P(B | C') * P(A') * P(C | A'))]

             = 1 - 0

             = 1

Therefore, the probability that sensor L detects motion given that there is movement outside and sensor V does not detect motion is 1.

(b) To find the probability that the home security system alerts the police given that there is a moving object, we need to consider the different combinations of sensor detections.

Let's denote the events as follows:

D = The home security system alerts the police

M = There is a moving object

We need to calculate P(D | M). This can occur in two ways:

1. Both sensor V and sensor L detect motion.

2. Sensor L detects motion while sensor V does not.

Using the law of total probability:

P(D | M) = P(D, V detects motion, L detects motion | M) + P(D, V does not detect motion, L detects motion | M)

We know:

P(D, V detects motion, L detects motion | M) = P(V detects motion | M) * P(L detects motion | M) = 0.95 * 0.8 = 0.76

P(D, V does not detect motion, L detects motion | M) = P(V does not detect motion | M) * P(L detects motion | M) = (1 - 0.95) * 0.8 = 0.04

Substituting

these values:

P(D | M) = 0.76 + 0.04

        = 0.8

Therefore, the probability that the home security system alerts the police given that there is a moving object is 0.8.

(c) To find the probability of a false alarm, i.e., that there is no movement but the police are alerted anyway, we need to consider the different combinations of sensor detections.

Let's denote the events as follows:

D = The home security system alerts the police

NM = There is no movement

We need to calculate P(D | NM). This can occur in two ways:

1. Both sensor V and sensor L detect motion.

2. Sensor L detects motion while sensor V does not.

Using the law of total probability:

P(D | NM) = P(D, V detects motion, L detects motion | NM) + P(D, V does not detect motion, L detects motion | NM)

We know:

P(D, V detects motion, L detects motion | NM) = P(V detects motion | NM) * P(L detects motion | NM) = 0.1 * 0.05 = 0.005

P(D, V does not detect motion, L detects motion | NM) = P(V does not detect motion | NM) * P(L detects motion | NM) = (1 - 0.1) * 0.05 = 0.045

Substituting these values:

P(D | NM) = 0.005 + 0.045

         = 0.05

Therefore, the probability of a false alarm, i.e., that there is no movement but the police are alerted anyway, is 0.05.

(d) To find the probability that there is a moving object given that both sensors detect motion, we can use Bayes' theorem.

Let's denote the events as follows:

M = There is a moving object

V = Sensor V detects motion

L = Sensor L detects motion

We want to find P(M | V, L).

Using Bayes' theorem:

P(M | V, L) = [P(V, L | M) * P(M)] / [P(V, L)]

We can calculate the values required:

P(V, L | M) = P(V | M) * P(L | M) = 0.95 * 0.8 = 0.76

P(M) = 0.7 (given probability of movement)

P(V, L) = P(V, L | M) * P(M) + P(V, L | M') * P(M')

        = 0.76 * 0.7 + 0.04 * 0.3

        = 0.532 + 0.012

        = 0.544

Substituting these values:

P(M | V, L) = (0.76 * 0.7) / 0.544

           ≈ 0.98

To know more about probability visit:

brainly.com/question/31828911

#SPJ11

Answer:

|a+5|=a+5

Step-by-step explanation:

if a>-5 or a= -5 |a+5|=a+5

if a< -5 |a+5|= -a-5

Answer:

900

Step-by-step explanation:

The biker travels 15 m/s and if there are 60 seconds, you multiply 15*60. The answer is 900

Answer:

900 meters

Step-by-step explanation:

The biker can go 15 meters in 1 second.

30 in 2 seconds.... etc etc

To find the length of the street we would multiply his speed (15 m/s) by the amount of seconds (60).

15 * 60 = 900

So, the street was 900 meters

The area painted red on one of the front wheels on DeMarius’ car will be 80.42 inches².

From the information given, the The front wheels on DeMarius’ car are divided into sectors of equal area and the radius of each wheel is 8 inches. The area will be:

= 2/5 × πr²

= 0.4 × 3.14 × 8²

= 80.42 inches²

The radius, in feet, of a rear wheel on the car will be:

r1(2π) = r2(2π)

8(2π) = r2(8/5)(2π)

16 = r2(8/5)

r = 5/8 × 16

r = 10 inches

r = (5/6) feet

Learn more about area on:

https://brainly.com/question/25292087

#SPJ1

Answer:

Step-by-step explanation:

In school i did these but i have no clue how to do them.I will try though:)

Answer:

-3, 3, 9

Step-by-step explanation:

Answer on Edge

Answer: the opposite of 15

Step-by-step explanation:

Answer:

12 sales

Step-by-step explanation:

a and b

65 per sale maximum commision 1300 so no base

40 per sale base 300

Set up equation:

\(65x=40x+300\)

Solve:

\(25x=300\)

\(x=12\)

So they must have had 12 sales.

Hope this helps :D

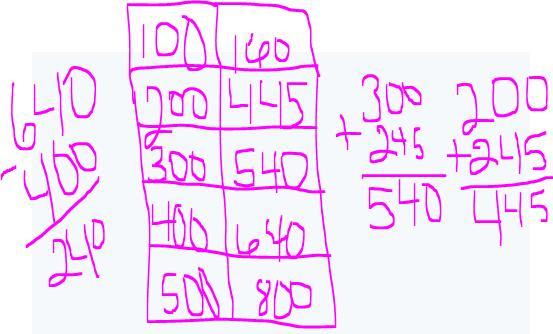
Answer 200 to 520 and 300 to 580.

Step-by-step explanation:

Each one increases by 60.

Answer:

They are adding 240 each time so; I'm a little unsure because the top is 160 and that's only 60 but...

Step-by-step explanation:

The linear transformations for the given values are:

t(1) = 0, t(x) = -8, t(x^2) = -3, t(ax^2 + bx + c) = -3a - 8b

To find the values of t(1), t(x), t(x^2), and t(ax^2 + bx + c), we need to use the given definitions of the linear transformation t.

We have:

t(-2x^2) = 2x^2 - 3x

t(0.5x - 3) = -2x^2 - 2x - 4

t(3x^2 + 1) = -3x^2

To find t(1), we substitute x = 0 into t(-2x^2) since -2x^2 represents the constant term in the polynomial:

t(-2(0)^2) = 2(0)^2 - 3(0)

t(0) = 0 - 0

t(0) = 0

Therefore, t(1) = 0.

To find t(x), we substitute x = 1 into t(0.5x - 3) since 0.5x - 3 represents the linear term in the polynomial:

t(0.5(1) - 3) = -2(1)^2 - 2(1) - 4

t(-2.5) = -2 - 2 - 4

t(-2.5) = -8

Therefore, t(x) = -8.

To find t(x^2), we substitute x = 1 into t(3x^2 + 1) since 3x^2 + 1 represents the quadratic term in the polynomial:

t(3(1)^2 + 1) = -3(1)^2

t(4) = -3

t(4) = -3

Therefore, t(x^2) = -3.

To find t(ax^2 + bx + c), we substitute the given expression into the definition of the linear transformation t:

t(ax^2 + bx + c) = a*t(x^2) + b*t(x) + c*t(1)

t(ax^2 + bx + c) = a*(-3) + b*(-8) + c*0

t(ax^2 + bx + c) = -3a - 8b

Therefore, t(ax^2 + bx + c) = -3a - 8b.

To know more about linear transformations refer here:

https://brainly.com/question/13595405#

#SPJ11

answer:

x^7 over x^4

step-by-step explanation:

hope this helps <3

Answer:

x^7 over x^4

Step-by-step explanation:

Happy to help

Answer:

step 2; a negative times a negative = a positive.

Step-by-step explanation:

-4(6-b)=4

-24 +4b=4

4b=28

b=7

Answer:

1 hour and 40 minutes

Step-by-step explanation:

60 minutes in an hour

we have 100 minutes

100 - 60 = 40

in 100 minutes we already have 1 hour

now we have 40 minutes left

can 40 minutes make another 60?

No.

so 100 minutes make

The correct pair of constraints that needs to be added to specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units is: P24 - P25 <= 80; P25-P24 <= 80. Therefore, the correct option is 5.

Here, the given information is Pij = the production of product i in period j. We need to find the pair of constraints that will specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units. Thus, let the production of product 2 in period 4 and in period 5 be represented as P24 and P25 respectively.

Therefore, we can write the following inequalities:

P24 - P25 <= 80

This is because the production of product 2 in period 5 can be at most 80 units less than that of period 4. This inequality represents the difference being less than or equal to 80 units.

P25-P24 <= 80

This is because the production of product 2 in period 5 can be at most 80 units more than that of period 4. This inequality represents the difference being less than or equal to 80 units.

Therefore, we need to add the pair of constraints P24 - P25 <= 80 and P25-P24 <= 80 to specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units. Hence, option 5 is the correct answer.

Learn more about Constraints:

https://brainly.com/question/3469433

#SPJ11

It would take 28 minutes to evacuate 21,000 people from the Wild Wind Stadium using only 15 exits

The time to evacuate the stadium varies directly with the number of people and inversely with the number of exits used. This means that the time it takes to evacuate the stadium is proportional to the number of people and inversely proportional to the number of exits used.

Let t be the time it takes to evacuate 21,000 people if only 15 exits are used. Let k be a constant of proportionality. Then we have

t = k × (number of people) / (number of exits)

We know that it takes 20 minutes to evacuate the stadium with all 25 exits in use. This gives us another equation

20 = k × 25000 / 25

Simplifying this equation, we get

20 = 1000k

k = 0.02

Now we can use this value of k to find the time it takes to evacuate 21,000 people with only 15 exits

t = 0.02 × 21000 / 15

t = 28 minutes

Learn more about equation here

brainly.com/question/14603452

#SPJ4

Based on the given dataset and information that the last digit of the CUNY ID is 5, the following steps are taken to analyze the data. The OLS estimates of coefficients B and β are calculated, and the predicted values of Y for each observation are determined. Residuals are calculated, along with the explained sum of squares (ESS), total sum of squares (TSS), and residual sum of squares (RSS). The coefficient of determination (R²) is calculated to assess the goodness of fit. Finally, the predicted value of Y is determined when X is equal to the last digit of the CUNY ID + 1.

a) To regress Y on X, we use ordinary least squares (OLS) estimation. The OLS estimates of coefficients B and β represent the intercept and slope, respectively, of the regression line. The coefficients are determined by minimizing the sum of squared residuals.

b) The predicted value of Y for each observation is obtained by plugging the corresponding X values into the regression equation. In this case, since the last digit of the CUNY ID is 5, the predicted value of Y would be calculated for X = 5.

c) Residuals are the differences between the observed Y values and the predicted Y values obtained from the regression equation. To calculate the residual for each observation, we subtract the predicted Y value from the corresponding observed Y value.

d) The explained sum of squares (ESS) measures the variability in Y explained by the regression model, which is calculated as the sum of squared differences between the predicted Y values and the mean of Y. The total sum of squares (TSS) represents the total variability in Y, calculated as the sum of squared differences between the observed Y values and the mean of Y. The residual sum of squares (RSS) captures the unexplained variability in Y, calculated as the sum of squared residuals.

e) The coefficient of determination, denoted as R², is a measure of the proportion of variability in Y that can be explained by the regression model. It is calculated as the ratio of the explained sum of squares (ESS) to the total sum of squares (TSS).

f) To predict the value of Y when X equals the last digit of the CUNY ID + 1, we can substitute this value into the regression equation and calculate the corresponding predicted Y value.

g) The coefficient B represents the intercept of the regression line, indicating the expected value of Y when X is equal to zero. The coefficient β represents the slope of the regression line, indicating the change in Y associated with a one-unit increase in X. The interpretation of β depends on the context of the data and the units in which X and Y are measured.

To learn more about regression click here: brainly.com/question/32505018

#SPJ11

Answer:

(x + 8) / 6

Step-by-step explanation:

The sum of x and 8, meaning x + 8 is being divided by six, so we group x + 8 in parentheses, and divide by 6 to get the answer

Answer:

true

Step-by-step explanation:

mean we show up the distribution

Answer:

90

Step-by-step explanation:

a right angle is always 90 degrees

In this situation, the probability that the researcher is making a Type I error is less than 1%.

Type I error refers to the rejection of a true null hypothesis, while Type II error refers to the failure to reject a false null hypothesis.

In this situation, since the alpha level is set to .01, the probability of making a Type I error (i.e., rejecting a true null hypothesis) is less than 1%, while the probability of making a Type II error (i.e., failing to reject a false null hypothesis) cannot be determined without knowing the effect size, sample size, and power of the study.

When a researcher reports a significant correlation using an alpha level of .01, it means that the probability of obtaining such a result by chance is less than 1%. However, this does not guarantee that the correlation is necessarily true or meaningful. There is always a possibility that the result is due to chance or other extraneous factors.

Therefore, the probability that the researcher is making a Type I error is less than 1%.

Learn more bout researcher here:

brainly.com/question/24174276

#SPJ4

Using the above graph, we can calculate that the segment has a length of 8 units.

The graph shows the segment and dimensions given at the end of the segment are -4 and 4.

Thus we can say that, the first half of the segment is having the length 4 units and the other half also has the same length of 4 units.

By, adding both these lengths we get,

4 + 4 = 8 units

Therefore, the length of the segment is 8 units which is computed using the given graph.

Learn more about line segment here:

https://brainly.com/question/27656385

#SPJ1

The length of 12cm on the map represents an actual distance of 0.0012 meters in the real world.

The map ratio of 1:10,000 means that one unit of measurement on the map represents 10,000 units of measurement in the real world.

In this case, the units of measurement are centimeters on the map and meters in the real world.

If a length on the map is 12cm, we can use the map ratio to calculate the actual distance it represents in meters.

Multiplying the length on the map by the ratio and then converting the result to meters:

12 cm × 1/10,000 = 0.0012 meters

Therefore, a length of 12cm on the map represents an actual distance of 0.0012 meters in the real world.

Learn more about the map ratio here:

https://brainly.com/question/15529349

#SPJ9

Solution :

Given :

n = 200, p = 80% = 0.8, q = 1 - p = 0.2

\($\mu = np$\)

  \($= 200 \times 0.8 = 160$\)

\($\sigma= \sqrt{npq}$\)

\($\sigma= \sqrt{200 \times 0.8 \times 0.2}$\)

   = 5.6569

a). x = 169.5

∴ \($z = \frac{x- \mu}{\sigma}$\)

  \($z = \frac{169.5- 160}{5.6569}$\)

     = 1.6794

\($P(x \geq 170) = P(z>1.6794) = 0.0465$\)

Therefore, probability that the stolen goods were not recovered in 170 robberies or more is = 0.0465

b). x= 149.5

   \($z = \frac{x- \mu}{\sigma}$\)

   \($z = \frac{149.5- 160}{5.6569} = -1.8561$\)

\($P(x \geq 150) = P(z>-1.8561) = 0.9683$\)

Therefore the probability that the stolen goods were not recovered in the 150 or in more robberies is = 0.9683

The polar curve r = 4 - 4sinθ, 0 ≤ θ < 2π has vertical tangent lines at θ = π/6 and θ = 7π/6.

To find the points where the polar curve has a vertical tangent line, we need to determine the values of θ for which the derivative of r with respect to θ, dr/dθ, is equal to infinity.

The derivative of r with respect to θ can be found using the chain rule of calculus. We have:

dr/dθ = d(4 - 4sinθ)/dθ

Differentiating the expression, we get:

dr/dθ = -4cosθ

For a vertical tangent line, the slope of the tangent line should be infinite, which means the derivative dr/dθ should be equal to infinity. Therefore, we set -4cosθ equal to infinity and solve for θ:

-4cosθ = ∞

Since the cosine function oscillates between -1 and 1, it never attains the value of infinity. However, there are two specific values of θ for which the cosine is equal to zero, resulting in the derivative being undefined (i.e., vertical tangent lines). These values are:

θ = π/2 + 2πk, where k is an integer

Converting these values to the range 0 ≤ θ < 2π, we have:

θ = π/2 and θ = 3π/2

Substituting these values back into the polar equation, we find the corresponding points on the curve:

For θ = π/2:

r = 4 - 4sin(π/2) = 4 - 4(1) = 0

For θ = 3π/2:

r = 4 - 4sin(3π/2) = 4 - 4(-1) = 8

Therefore, the polar curve r = 4 - 4sinθ has vertical tangent lines at the points (0, π/2) and (8, 3π/2).

Learn more about polar curves

brainly.com/question/28976035

#SPJ11

Yes, I can find the slope of a line and type the correct code. The SLOPE function will return the slope of the linear regression line that best fits the data.

The slope of a line is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. The formula for finding the slope of a line is (y2 - y1)/(x2 - x1), where (x1, y1) and (x2, y2) are any two points on the line.

The slope is a measure of how steep the line is. It can be positive, negative, zero, or undefined. The code for finding the slope of a line in ALL CAPS with no spaces is SLOPE.

To use this function in Excel, you need to provide the range of x-values and the range of y-values.

To learn more about : slope

https://brainly.com/question/16949303

#SPJ11