how much paper is used in the label for the can of cat food? Round your answer to the nearest whole number
Answers
TLDR Multiply circumference of top of can & height of can
Related Questions
what happens when you raise -2 to a power
Answers
Answer: it becomes a positive
Step-by-step explanation:
Write a system of linear inequalities represented by the graph.
Inequality 1:
Inequality 2:

Answers
A system of linear inequalities represented by the graph are;
y > x - 2
y < 5x + 1
How to write a system of Inequalities?The general form of the equation of a line in slope intercept form is;
y = mx + c
where;
m is slope
c is y-intercept
The broken(dashed line) has the y-intercept as -2.
The slope is;
m = (0 - (-2))/(2 - 0)
m = 1
However, it is shaded above the line which means the equation is;
y > x - 2
The second line which is a solid line has the y-intercept as 1.
The slope is calculated as;
m = (-4 - 1)/(-1 - 0)
m = 5
The shaded part is below the line which denotes;
y < 5x + 1
Read more about System of Inequalities at; https://brainly.com/question/25275758
#SPJ1
um I need help with thissss

Answers
Answer:
its you again
Step-by-step explanation:
if they have the same amount of dashes on the same sided they are congruent
does that answer your question
if they have the same amount of dashes on the same sided they are congruent
y+2=-3(x+2) in slope intercept form
Answers
y = -3x - 8
Slope-intercept form: y = mx + b
Given: y + 2 = -3(x + 2)
Simplify:
y + 2 = -3x - 6
y = -3x - 6 - 2
y = -3x - 8
We have: m = -3, and b = -8
Answer:
y=-3x-8
Step-by-step explanation:
First make y by itself
y=-3(x+2)-2
Distribute the -3
y=-3x-6-2
Combine like terms
y=-3x-8
You save $8,500.00. You place 40% in a savings account earning a 4.2% APR compounded annually and the rest in a stock plan. The stock plan decreases 3% in the first year and increases 7.5% in the second year.
A. What is the total gain at the end of the second year for both accounts combined?
B. If you had invested 60% in the savings account and the rest in the stock plan, what is the difference in the total gain compared to the original plan?
Answers
The total gain at the end of the second year for both accounts combined is $509.09.
We have,
Amount saved = $8500
40% of 8500 is saved in saving account = 0.4 x 8500 = $3400
Remainder amount in stock plan = 8500 - 3400 = 5100
Working for savings plan
A = P(1 + r/n\()^{nt\)
A = 3400(1 + 0.042/1)²
A = $3691.60
So, we gain = 3691.6 - 3400 = $291.6
Working for stock plan:
The stock plan decreases 3% in the first year
= 5100 x 0.97
= $4947
and increases 7.5% in the second year.
= 4947 x 1.75
= $5318.03
So, we gain = 5318.03 - 5100 = $218.03
Thus, the total gain is
= 291.06 + 218.03
= $509.09
Learn more about Compound Interest here:
https://brainly.com/question/14295570
#SPJ1
John wants to buy strawberries and apples to make a fruit tart. Strawberries cost $3 per pound and apples cost $2.25 per pound. How much does he spend if he buys 0.5 pounds of strawberries and 3 pounds of apples? How much does he spend if he buys xx pounds of strawberries and yy pounds of apples?
Answers
Answer:
he spends $1.5 on strawberries and $6.75 on apples
(a) What is the area of the triangle determined by the lines y = - --- x + 9, y 10x, and the y-axis? 27/7 (b) If b> 0 and m< 0, then the line y = mx + b cuts off a triangle from the first quadrant. Express the area of that triangle in terms of m and b. 2m X (c) The lines y = mx + 5, y = x, and the y-axis form a triangle in the first quadrant. Suppose this triangle has an area of 10 square units. Find m. m = -1/4 Additional Materials Reading
Answers
(a) The area of the triangle determined by the lines y = -x + 9, y = 10x, and the y-axis is 0 square units.
(b) The area of the triangle determined by the line y = mx + b, where b > 0 and m < 0, is -1/2 * (b^2 / m).
(c) There is no value of m that allows the triangle determined by the lines y = mx + 5, y = x, and the y-axis to have an area of 10 square units.
(a) The lines y = -x + 9, y = 10x, and the y-axis form a triangle in the first quadrant. To find the area of this triangle, we can calculate the base and height.
The base of the triangle is the x-coordinate where y = 0, which is the y-intercept of the line y = -x + 9. So, the base is 9.
The height of the triangle is the y-coordinate where x = 0, which is the y-intercept of the line y = 10x. So, the height is 0.
The area of a triangle is given by the formula: area = 1/2 * base * height.
Substituting the values we found:
Area = 1/2 * 9 * 0
Area = 0
The area of the triangle determined by the lines y = -x + 9, y = 10x, and the y-axis is 0 square units.
(b) If b > 0 and m < 0, then the line y = mx + b cuts off a triangle from the first quadrant. The base of this triangle is determined by the x-coordinate where y = 0, which is x = -b/m.
The height of the triangle is determined by the y-coordinate where x = 0, which is y = b.
The area of the triangle is given by the formula: area = 1/2 * base * height.
Substituting the values we found:
Area = 1/2 * (-b/m) * b
Area = -1/2 * (b^2 / m)
The area of the triangle determined by the line y = mx + b, where b > 0 and m < 0, is -1/2 * (b^2 / m).
(c) The lines y = mx + 5, y = x, and the y-axis form a triangle in the first quadrant. Given that this triangle has an area of 10 square units, we can find the value of m.
The base of the triangle is determined by the x-coordinate where y = 0, which is x = -5/m.
The height of the triangle is determined by the y-coordinate where x = 0, which is y = 0.
The area of the triangle is given by the formula: area = 1/2 * base * height.
Substituting the values we found and given that the area is 10:
10 = 1/2 * (-5/m) * 0
10 = 0
Since the equation 10 = 0 is not possible, there is no value of m that satisfies the condition.
There is no value of m that allows the triangle determined by the lines y = mx + 5, y = x, and the y-axis to have an area of 10 square units.
To know more about square units, visit
https://brainly.com/question/2411992
#SPJ11
Apply all relevant properties of

Answers
Recall that, when two terms are being multiplied and they have the same number we can add the exponents:
\(x^nx^m=x^{n+m}.\)Applying the above property to the given expressions, we get:
\(\begin{gathered} 6^{\frac{9}{5}}6^{\frac{1}{5}}=6^{\frac{9}{5}+\frac{1}{5}}, \\ x^{\frac{10}{3}}x^{\frac{11}{3}}=x^{\frac{10}{3}+\frac{11}{3}}, \\ y^{\frac{7}{2}}y^{\frac{1}{2}}=y^{\frac{7}{2}+\frac{1}{2}}. \end{gathered}\)Simplifying the above results, we get:
\(\begin{gathered} 6^{\frac{9}{5}}6^{\frac{1}{5}}=6^2, \\ x^{\frac{10}{3}}x^{\frac{11}{3}}=x^7, \\ y^{\frac{7}{2}}y^{\frac{1}{2}}=y^4. \end{gathered}\)Answer:
\(\begin{gathered} 6^{\frac{9}{5}}6^{\frac{1}{5}}=6^2, \\ x^{\frac{10}{3}}x^{\frac{11}{3}}=x^7, \\ y^{\frac{7}{2}}y^{\frac{1}{2}}=y^4. \end{gathered}\)hey! i’ll give brainliest please help

Answers
Answer:
It's the second one, two independent clauses connected by a conjunction
please help me do this question in the screenshot. I will give you stars for it!

Answers
Let's see
\(\\ \rm\Rrightarrow \dfrac{10}{12}\times \dfrac{6}{9}\)
\(\\ \rm\Rrightarrow \dfrac{5}{6}\times \dfrac{2}{3}\)
\(\\ \rm\Rrightarrow \dfrac{10}{18}\)
\(\\ \rm\Rrightarrow \dfrac{5}{9}\)
what justifies the use of the normal distribution for the sampling distribution of the proportion?
Answers
The ability of the normal distribution to approximate the binomial distribution under appropriate conditions justifies the use of the normal distribution for the sampling distribution of the proportion.
A sampling distribution is a statistical probability distribution derived from a larger number of samples gathered from a certain population. The sampling distribution of a particular population is the distribution of frequencies of a range of possible outcomes for a population statistic.
A population is the whole pool from which a statistical sample is selected in statistics. A population can be defined as a large group of people, things, events, medical visits, or measures. A population can thus be defined as an aggregate observation of persons linked by a common trait.
Learn more about Sampling Distribution:
https://brainly.com/question/29368683
#SPJ4
Use graph to work out x and y

Answers
Answer: x = 1, y = 4
Step-by-step explanation:
First, you would need to set the equations equal to each other.
y = 3x + 1 and y = -2x + 6
They can be set equal to each other because they are equal to the same y.
So, you would get the equation:
3x + 1 = -2x + 6
From there, solve for x.
3x + 2x = 6 - 1
5x = 5
x = 1
Now, plug that x-value into the original equations to get y.
y = 3(1) +1
= 3 + 1
= 4
Plug the x-value into the other equation and if you get the same answer, you're correct!
y = -2(1) + 6
= -2 + 6
= 4
So, as an ordered pair (in the form [x, y]), the answer would be (1, 4).
What is the equivalent ratio 9 over 11 and nothing over 99
Answers
Answer:
18/22
27/33
36/44
45/55
help appreciated thanks

Answers
Answer:
No
Step-by-step explanation:
x=(b-5)/c≠(5-b)/c
supposedly
b=6
c=1
x=6-5/1=1
x=5-6/1= -1
1≠ -1
Answer:
No
Step-by-step explanation:
x = b - 5 / L equal to - (5 - b) / L
Romeo prepares flower bouquets of different sizes using a ratio of 2 babys breath steams for every 3 roses
Answers
Answer: If you have a boquet with 20 items with a ratio of 2:3 (baby breath to roses), then you have 8 red roses to 12 baby breath stems.
NOTE: Please let me know if you have a different scenario to solve.
Step-by-step explanation:
The ratio is (baby breath) 2:3 (roses)
Red roses are 2x and baby breath is 3x
Solve for a boquet containing 20 stems:
2x+3x= 20
5x=20
x=20/5
x=4
Red roses: 2x = 8 stems
Baby breath: 3x = 12 stems
P(Z≤b)=0.0311 b ? a. −1.87 b. −1.86 c. −1.8 d. −1.865
Answers
The answer is option d. -1.865, as it is the value that satisfies P(Z ≤ b) = 0.0311. The other options (-1.87, -1.86, -1.8) do not correspond to the given cumulative probability.
In this scenario, P(Z ≤ b) represents the cumulative probability of a standard normal distribution up to the value of b. To find the corresponding value of b, we need to find the z-score that corresponds to a cumulative probability of 0.0311.
By looking up the z-table or using a statistical calculator, we can find that the z-score corresponding to a cumulative probability of 0.0311 is approximately -1.865.
Therefore, the answer is option d. -1.865, as it is the value that satisfies P(Z ≤ b) = 0.0311. The other options (-1.87, -1.86, -1.8) do not correspond to the given cumulative probability.
Learn more about probability:
https://brainly.com/question/31828911
#SPJ11
722000
= ×10
its scientific notation help please
Answers
Answer:
7.22 x 10^5
Step-by-step explanation:
Remember that the decimal is always to the right of the ones place.
1. Move it one place to the left and multiply by 10 to compensate.
2. Move it two places to left and multiply by 10^2.
3. Move the decimal point three times and multiply 10^3 to compensate, and the pattern continues until you reach the very last digit, the 7.
4. Numbers after the 7 that are not zeros will be after the decimal point.
so, 7.22 x 10^5
79 tens X 27 tens with rounding
Answers

factorise fully x^2 +6x+9
Answers
Answer:
x= -3, x= -3
Step-by-step explanation:
x²+6x+9
ax²+bx+c=0
where a=1,b=6,c=9
using factorisation method
the two factors are 3 and 3
x²+3x+3x+9=0
x(x+3)+3(x+3)=0
(x+3)(x+3)=0
x+3=0 or x+3=0
x=-3,x= -3
(15 POINTS) please please help out if you can!! I Will mark you brain list!! I also have other things on my account for a lot of points! If you could help that would help so so much!!

Answers
Answer:
(2w+2)(w+8) ≤ 100
Step-by-step explanation:
A = l x w
we want less than or equal to 100
100 ≥ length (2w +2) x width (w+8)
flip around to look like answer
8) A normally distributed set of population scores has a mean of 65 and a standard deviation of 10.2. The mean, of the sampling distribution of the mean, for samples of size 48 equals _________.
9) For the population and sample size given in question 8, the standard error of the mean equals _________.
Answers
For samples of size 48, the mean of the sampling distribution of the mean is 65 and the standard error of the mean is approximately 1.477.
As given, A normally distributed set of population scores has a mean of 65 and a standard deviation of 10.2. Therefore, μ = 65 and σ = 10.2For samples of size n = 48, the mean of the sampling distribution of the mean will be the same as the population mean: μ_M = μ = 65 Hence, the mean of the sampling distribution of the mean is 65.
9) For the population and sample size given in question 8, the standard error of the mean can be calculated using the formula: SEM = σ/√where σ = standard deviation of the population = sample size Substituting the values in the formula, we get: SEM = 10.2/√48 ≈ 1.477Hence, the standard error of the mean is approximately 1.477.
Answer: For samples of size 48, the mean of the sampling distribution of the mean is 65 and the standard error of the mean is approximately 1.477.
SPJ11
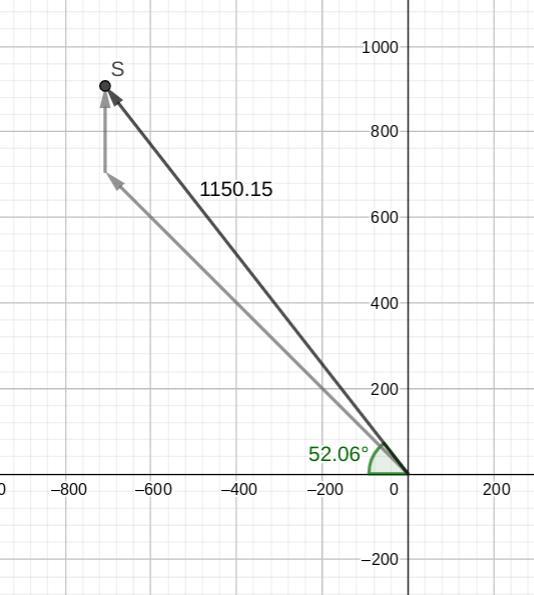
Caroline leaves her apartment and walks 45° north of west for 1000 feet and then walks 200 feet due north to go to the grocery store. How far and at what north of west
quadrant is Caroline from being at her apartment?
Answers
Answer:
1150 ft W 52° N
Step-by-step explanation:
There are several ways a problem like this can be solved. Perhaps the easiest is to make use of a suitable vector calculator.
Using West as the reference for angles measured clockwise (toward north), the final position is ...
1000∠45° +200∠90° = 1150.149∠52.063°
__
You can also figure this using the Law of Cosines. It will tell you the resultant distance (c) in terms of the individual distances (a, b) and the angle between them (135°).
c² = a² +b² -2ab·cos(C)
c² = 1000² +200² -2·1000·200·cos(135°) ≈ 1,322,842.7
c ≈ √1322842.7 ≈ 1150.149
The angle difference from 45°N can be found using the Law of Sines.
sin(B)/b = sin(C)/c
B = arcsin(b/c·sin(C)) = arcsin(200/1140.149·sin(135°)) ≈ 7.063°
This means Caroline's bearing from home is 45° +7.063° ≈ 52° north of west.
Caroline's final position is 1150 W 52° N in relation to her home.
Tim answered all the questions on his math test but got
10 answers wrong. He received 4 points for every correct answer, and there was no penalty for wrong answers. His score was 76 points.
Pls I need the equations ASAP
Answers
Answer:
29 questions total
Step-by-step explanation:
Since his score was 76 points and he received 4 points per correct answer, you can find the number of correct answers by dividing 76 by 4
76/4 = 19
The you add to that the number of questions he got wrong:
19 + 10 = 29 total questions.
Can two equilateral triangles always be congruent Is it true or false?
Answers
Must use these cases for congruent
Must use at least one angle are congruent in each triangle
If a figure is a square, its diagonals divide it into isosceles triangles.
p: A figure is a square.
q: A figure's diagonals divide into isosceles triangles.
Which represents the converse of this statement? Is the converse true?
Answers
The converse of the statement "If a figure is a square, its diagonals divide it into isosceles triangles" would be:
"If a figure's diagonals divide it into isosceles triangles, then the figure is a square."
The converse statement is not necessarily true. While it is true that in a square, the diagonals divide it into isosceles triangles, the converse does not hold. There are other shapes, such as rectangles and rhombuses, whose diagonals also divide them into isosceles triangles, but they are not squares. Therefore, the converse of the statement is not always true.
Therefore, the converse of the given statement is not true. The existence of diagonals dividing a figure into isosceles triangles does not guarantee that the figure is a square. It is possible for other shapes to exhibit this property as well.
In conclusion, the converse statement does not hold for all figures. It is important to note that the converse of a true statement is not always true, and separate analysis is required to determine the validity of the converse in specific cases.
for similar questions on triangles.
https://brainly.com/question/1058720
#SPJ8
A retail establishment closes each evening. If the establishment is open from 9 am to 5 pm, the objective of a simulation might be to estimate some measure of the
quality of customer service over the period beginning at 9 am and ending when the last customer who entered before the doors closed 5 pm has been served.
What type of model is the above model according to the output analysis?
Answers
According to the output analysis, the model presented above is of Discrete-event simulation (DES) type.
What is Discrete-event simulation (DES)?
Discrete-event simulation (DES) is indeed a type of computer-based simulation where events occur at specific points in time. In DES, a system's behavior is modeled by specifying the sequence of events that occur during the system's lifespan.
In a discrete-event simulation, the state of the system changes only when events occur, rather than continuously evolving over time. Events represent significant occurrences or activities within the system, such as customer arrivals, service completions, or resource allocations. Each event is associated with a specific time or occurrence point, and the simulation progresses by processing events in chronological order.
DES is particularly useful for modeling complex systems where the timing of events and their interactions play a crucial role. It allows for capturing the dynamic nature of the system, simulating the flow of entities (such as customers, vehicles, or messages) through the system, and observing the effects of event sequencing and resource allocation on system performance.
By simulating the system and observing the events and their consequences, DES enables analysts to evaluate different scenarios, study the impact of various parameters, and optimize system design or operation. It provides insights into system performance measures, such as throughput, waiting times, resource utilization, or customer satisfaction.
Overall, discrete-event simulation is a powerful technique for modeling and analyzing complex systems with discrete changes, events, and interactions over time.
To know more about output analysis visit:
https://brainly.com/question/14770927
#SPJ11
The model above is known as a discrete-event simulation model according to the output analysis.
A discrete event simulation is a type of computer-based modeling where a series of discrete events in a system are simulated.
In such models, the system under consideration evolves through a series of discrete events that are instantaneous.
For example, in the retail establishment model, each customer arriving at the store would be considered a separate, discrete event.
The simulation would model the sequence of events that occur between the time the store opens at 9 am and when the last customer leaves before closing time at 5 pm.
The objective of the simulation would be to estimate some measure of the quality of customer service during this time period.
To know more about discrete-event simulation model visit:
https://brainly.com/question/33571729
#SPJ11
Solve for x. Round your answer to the nearest thousandth. a. 8.691 c. 6.474 b. 6.252 d. 12.956

Answers
Answer:
The answer is B 6.252
Step-by-step explanation:
The Wagner Corporation has a $22 million bond obligation outstanding, which it is considering refunding. Though the bonds were initially issued at 12 percent, the interest rates on similar issues have declined to 10 percent. The bonds were originally issued for 20 years and have 16 years remaining. The new issue would be for 16 years. There is a 7 percent call premium on the old issue. The underwriting cost on the new $22 million issue is $680,000, and the underwriting cost on the old issue was $530,000. The company is in a 40 percent tax bracket, and it will allow an overlap period of one month ( 1/12 of the year). Treasury bills currently yield 5 percent. (Do not round intermediate calculations. Enter the answers in whole dollars, not in millions. Round the final answers to nearest whole dollar.) a. Calculate the present value of total outflows. Total outflows b. Calculate the present value of total inflows. Total inflows $ c. Calculate the net present value. Net present value $ d. Should the old issue be refunded with new debt? Yes No
Answers
The answer are: a. Total outflows: $2,007,901, b. Total inflows: $827,080, c. Net present value: $824,179, d. Should the old issue be refunded with new debt? Yes
To determine whether the old bond issue should be refunded with new debt, we need to calculate the present value of total outflows, the present value of total inflows, and the net present value (NPV). Let's calculate each of these values step by step: Calculate the present value of total outflows. The total outflows consist of the call premium, underwriting cost on the old issue, and underwriting cost on the new issue. Since these costs are one-time payments, we can calculate their present value using the formula: PV = Cash Flow / (1 + r)^t, where PV is the present value, Cash Flow is the cash payment, r is the discount rate, and t is the time period.
Call premium on the old issue: PV_call = (7% of $22 million) / (1 + 0.1)^16, Underwriting cost on the old issue: PV_underwriting_old = $530,000 / (1 + 0.1)^16, Underwriting cost on the new issue: PV_underwriting_new = $680,000 / (1 + 0.1)^16. Total present value of outflows: PV_outflows = PV_call + PV_underwriting_old + PV_underwriting_new. Calculate the present value of total inflows. The total inflows consist of the interest savings and the tax savings resulting from the interest expense deduction. Since these cash flows occur annually, we can calculate their present value using the formula: PV = CF * [1 - (1 + r)^(-t)] / r, where CF is the cash flow, r is the discount rate, and t is the time period.
Interest savings: CF_interest = (12% - 10%) * $22 million, Tax savings: CF_tax = (40% * interest expense * tax rate) * [1 - (1 + r)^(-t)] / r. Total present value of inflows: PV_inflows = CF_interest + CF_tax. Calculate the net present value (NPV). NPV = PV_inflows - PV_outflows Determine whether the old issue should be refunded with new debt. If NPV is positive, it indicates that the present value of inflows exceeds the present value of outflows, meaning the company would benefit from refunding the old issue with new debt. If NPV is negative, it suggests that the company should not proceed with the refunding.
Now let's calculate these values: PV_call = (0.07 * $22,000,000) / (1 + 0.1)^16, PV_underwriting_old = $530,000 / (1 + 0.1)^16, PV_underwriting_new = $680,000 / (1 + 0.1)^16, PV_outflows = PV_call + PV_underwriting_old + PV_underwriting_new. CF_interest = (0.12 - 0.1) * $22,000,000, CF_tax = (0.4 * interest expense * 0.4) * [1 - (1 + 0.1)^(-16)] / 0.1, PV_inflows = CF_interest + CF_tax. NPV = PV_inflows - PV_outflows. If NPV is positive, the old issue should be refunded with new debt. If NPV is negative, it should not.
Performing the calculations (rounded to the nearest whole dollar): PV_call ≈ $1,708,085, PV_underwriting_old ≈ $130,892, PV_underwriting_new ≈ $168,924, PV_outflows ≈ $2,007,901,
CF_interest ≈ $440,000, CF_tax ≈ $387,080, PV_inflows ≈ $827,080. NPV ≈ $824,179. Since NPV is positive ($824,179), the net present value suggests that the old bond issue should be refunded with new debt.
Therefore, the answers are:
a. Total outflows: $2,007,901
b. Total inflows: $827,080
c. Net present value: $824,179
d. Should the old issue be refunded with new debt? Yes
To learn more about tax, click here: brainly.com/question/31857425
#SPJ11
A sawoman cams 8% commission on at the merchandise that the sets Last month she sold $7000 worth of merchandise. How much commission (in dollars) did she warm last month?
Answers
He made $480 in commission last month
What is a Commission?This refers to the fee paid to an agent or employee for transacting a piece of business or performing a service
First, convert 8% into a decimal
8%/100
= 0.08
Multiply the decimal by his sales
0.08 * 6000
480
Therefore, he made $480 in commission last month
Read more about commissions here:
https://brainly.com/question/26283663
#SPJ1
The cost of using a game facility is $1 for every 12 minutes. Talisa writes the function for the cost per hour as
Answers
h=hours
$1 + 5m