Answers
Answer:
There is 8 vertices!
Step-by-step explanation:
They are just the points of the cube!
Hope this helps!
Related Questions
Pablo used a total of 5 3/4 gallons of gas while driving his car. Each hour he was driving, he used 5/6 gallons of gas. What was the total number of hours he was driving? Write your ans
Answers
We know that he used 5/6 gallons of gas per hour of driving.
So, the total amount of gas he used is 5/6 * x.
We also know that he used a total of 5 3/4 gallons of gas.
So, we can set up the equation:
5/6 * x = 5 3/4
To solve for x, we can first convert 5 3/4 to an improper fraction:
5 3/4 = 23/4
Then, we can multiply both sides of the equation by the reciprocal of 5/6:
x = (5 3/4) / (5/6)
x = (23/4) / (5/6)
x = (23/4) * (6/5)
x = 27.6/4
x = 6.9
Therefore, Pablo was driving for a total of 6.9 hours.
brainliest???
Answer the question on the image and why do you have that answer

Answers
Answer:
1km
Step-by-step explanation:
15 minutes is 1/4 of an hour
15/60 = 1/4
4 * 1/4 = 1
a media rental store rented the following number of movie titles in each of these categories: horror, drama, mystery, romance, and comedy. if a person selects a movie to rent, find the probability that it is a horror or comedy. enter your answer as a fraction or a decimal rounded to decimal places.
Answers
30.2% is the necessary probability that it is a horror or comedy movie title.
Given:
There are 168 films in the horror category.
There are 118 films in the mystery category.
The following formula can be used to get the total number of movies in the video rental store:
Total number of outcomes is = (168 + 220 + 118 + 308 + 134) =948
Let P (H) represent the likelihood that it will be a horror film, and P (M) represent the likelihood that it will be a mystery. In addition, we presumptively believe that a film can only fall into one of two categories: mystery or horror. The likelihood that a horror or mystery film will be chosen as a rental can be calculated as follows:
\(P(M or H) = P(H) + P(M)\)
\(=\frac{168}{948} +\frac{118}{948}\)
\(=\frac{168+118}{948}\)
\(=\frac{286}{948}\)
≈\(0.302\)
Therefore, 30.2% is the necessary probability.
Learn more about probability here:
https://brainly.com/question/14289833
#SPJ4
Write a multiplication sentence to show how 10 gallons and 300 miles are related. How are 5 gallons ad 150 miles related? How are 1 gallon and 30 miles related?
Answers
Answer:
It shows for each gallon consumed, we multiply by 30 to get the amount of miles
This applies for the three questions
Step-by-step explanation:
10 gallons and 300 miles are related in such a way that you divide the number if miles by number of gallons.
300/10 = 30 miles per gallon.
It shows for each gallon consumed, we multiply by 30 to get the amount of Miles.
5 gallons ad 150 miles related in such a way that you divide the number if miles by number of gallons.
150/5 = 30 miles per gallon.
It shows for each gallon consumed, we multiply by 30 to get the amount of Miles.
1 gallon and 30 miles related in such a way that you divide the number if miles by number of gallons.
30/1= 30 miles per gallon.
It shows for each gallon consumed, we multiply by 30 to get the amount of Miles.
In a class of 42 students, the number of boys is 2/5 of the girls. Find the number of boys and girls in the class.
Answers
Answer:
BOYS = 30.
GIRLS = 12.
Step-by-step explanation:
Boys: B
Girls: G
B = (2/5)G
B + G = 42.
(2/5)G + G = 42
2G + 5G = 210
7G = 210
G = 210/7
G = 30.
B = (2/5)G
B = (2/5)(30)
B = 60/5
B = 12.
Answer:
\(\Huge \boxed{\bold{\text{12 Boys}}}\)
\(\Huge \boxed{\bold{\text{30 Girls}}}\)
Step-by-step explanation:
Let the number of girls be \(g\) and the number of boys be \(b\).
According to the problem: \(b = \frac{2}{5} \times g\)
We also know that the total number of students is 42, so \(b + g = 42\).
Now, we have two equations with two variables:
\(b = \frac{2}{5} \times g\) \(b + g = 42\)We can solve these equations to find the values of \(b\) and \(g\).
Step 1: Solve for \(\bold{b}\) in terms of \(\bold{g}\)
From the first equation, we have\(b = \frac{2}{5} \times g\)
Step 2: Substitute the expression for \(\bold{b}\) into the second equation
Replace \(b\) in the second equation with the expression we found in step 1.
\(\frac{2}{5} \times g + g = 42\)
Step 3: Solve for \(\bold{g}\)
Now, we have an equation with only one variable, \(g\):
\(\frac{2}{5} \times g + g = 42\)
To solve for \(g\), first find a common denominator for the fractions:
\(\frac{2}{5} \times g + \frac{5}{5} \times g = 42\)
Combine the fractions:
\(\frac{7}{5} \times g = 42\)
Now, multiply both sides of the equation by \(\frac{5}{7}\) to isolate \(g\):
\(g = 42 \times \frac{5}{7}\)\(g = 30\)Step 4: Find the value of \(\bold{b}\)
Now that we have the value of \(g\), we can find the value of \(b\) using the first equation:
\(b = \frac{2}{5} \times g\)\(b = \frac{2}{5} \times 30\)\(b = 12\)So, there are 12 boys and 30 girls in the class.
----------------------------------------------------------------------------------------------------------
The number of students in nine faculties of a university are given as 168, 285, 397, 331, 383, 359, 366, 280 and 369 Find the mean number of students per Faculty
Answers
The mean number of students per Faculty is 326.
What is mean?Mean simply means the average of a set of numbers.
In this case, the number of students in nine faculties of a university are given as 168, 285, 397, 331, 383, 359, 366, 280 and 369. The mean will be:
= Total values / 9
= (168 + 285 + 397 + 331 + 383 + 359 + 366 + 280 + 369) / 9
= 2938 / 9
= 326.44
The mean is 326.
Learn more about mean on:
brainly.com/question/1136789
#SPJ1
Given T(x, y)=(x+2, y+5), state the translation S(x, y) that would yield the identity transformation, I=S(T(x,y)).
Answers
9514 1404 393
Answer:
S(x, y) = (x -2, y -5)
Step-by-step explanation:
Transformation T is a translation right 2 and up 5. The translation required to get the figure back to its original position is left 2 and down 5.
S(x, y) = (x -2, y -5)
Please help with these questions!

Answers
Answer:
please take a better picture, i can'r read it.
Step-by-step explanation:
PLEASE HELP I WILL MARK BRAINLYIST IF CORRECT The following graph shows a proportional relationship.
What is the constant of proportionality between y and x in the graph?
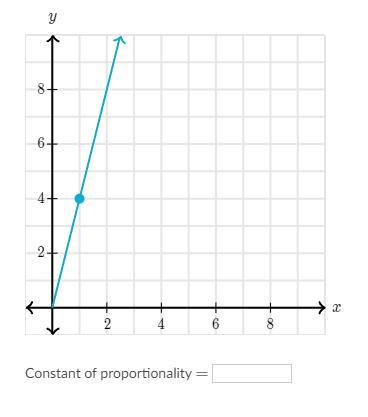
Answers
Match the inequality to the graph of its solution. (Write the letter of the multiple choice in lowercase)
A
\(c + 7 \leqslant 3\)
B
\(c - 3 > 1\)
C
\(c - 7 < 3\)
![Match the inequality to the graph of its solution. (Write the letter of the multiple choice in lowercase)A[tex]c](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/sPA5EjINgWGCZcMlAkaQjhdZAtmw7uS9.jpeg)
Answers
Explanation - The graph shoes the inequality c<10.
To work out the inequality, you have to add 7 to the 3 (7+3), which is equal to 10. That gives us the answer c<10.
Hope that makes sense :)
The inequality c - 7 > 3 is matched to the graph of its solution. The correct answer is option C.
As per the shown number line,
Here, the inequality is inclusive (c ≤ 10), and the point at 10 is included, so use a closed circle to mark the point.
An arrow extends to the left of the marked point. This arrow indicates all the values of c that are less than 10.
If the inequality is strict (c < 10), the arrow should be drawn with an open end.
Thus, the inequality c - 7 > 3 is matched to the graph of its solution.
Hence, the correct answer is option C.
Learn more about inequalities here:
brainly.com/question/20383699
#SPJ7
Find the measure of the indicated angle.
99⁰
96⁰
98⁰
92°
L
120°
K
N
M
64

Answers
Answer:
? = 92°
Step-by-step explanation:
the chord- chord angle ? is half the sum of the measures of the arcs intercepted by the angle and its vertical angle, that is
? = \(\frac{1}{2}\) (LM + AK) = \(\frac{1}{2}\) (120 + 64)° = \(\frac{1}{2}\) × 184° = 92°
.
A polling organization conducts a study to estimate the percentage of households that have high-speed Internet access. It mails a questionnaire to 1495 randomly
Internet access. Of the 1495 households selected, 22.
Answers
a) The best description of the bias in the survey is A. Nonresponse bias.
b) To remedy this bias, B. The polling organization should try contacting households that do not respond by phone or face-to-face.
What is nonresponse bias?Nonresponse bias is the type of bias when survey participants are not interested in the survey or send an empty or unsatisfactory response.
Nonresponse bias means that the sample is filled with those who are not willing or able to respond, making the number of non-respondents surpass the number of respondents.
Thus, a response of 22/1,495 is too significant to be ignored, meaning that the nonresponse bias is much more critical.
Learn more about types of survey bias at https://brainly.com/question/23260388
#SPJ1
Question Completion:responded.
a) Which of these best describes the bias in the survey?
A. Nonresponse bias
B. Sampling bias
C. Undercoverage bias
D. Response bias
b) How can the bias be remedied?
A. The polling organization should mail the questionnaire to a greater number of households.
B. The polling organization should try contacting households that do not respond by phone or face-to-face.
C. The polling organization should mail the questionnaire to each person in the household.
a landscape architect wishes to enclose a rectangular garden on one side by a brick wall costing $40/ft and on the other three sides by a metal fence costing $20/ft. if the area of the garden is 142 square feet, find the dimensions of the garden that minimize the cost.
Answers
The dimensions of the rectangular garden which minimize the cost is equal to 9.6ft and 14.6ft respectively.
As given in the question,
Cost of brick wall is equal to $40/ft
Cost of metal fencing is equal to $20/ft
Let 'x' and 'y' are the dimensions of the rectangular garden
Area of the rectangular garden = 142 square feet
⇒ 142 = xy
⇒x = 142/y
Costing of four side fencing 'C' = 40x + 20x + 20y + 20y
⇒ C = 60x + 40y
⇒C = 60(142/y) + 40y
⇒C = 8520/y + 40y
Differentiate with respect to y
dC/dy = -8520/ y² + 40
Put dC/dy = 0
-8520/ y² + 40 = 0
⇒y² = 8520/40
⇒y = √213
⇒ y= 14.6 ft
⇒ x= 142/14.6
= 9.7 ft
Therefore, the dimensions of the rectangular garden with the given area which minimize the cost is equal to 14.6ft and 9.7ft.
Learn more about rectangular here
brainly.com/question/21416050
#SPJ4
What is the answer of this triangle congruence question.

Answers
The value of x in the triangles are 9.
What is a quadratic equation?For variable x : ax² + bx + c = 0, where a≠0 is a standard quadratic equation, which is a second-order polynomial equation in a single variable. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem.
Given:
The triangles are congruent.
That means, their corresponding angles are also congruent.
In ΔJKL,
the sum of all the angles of the triangle is 180°.
So,
x²-2x + x + 29 + 3x + 52 = 180
x² + 2x - 99 = 0
Solving the quadratic equation,
x² +11x - 9x - 99 = 0.
x (x + 11) -9 (x + 11) = 0
x = 9 and x = -11
Here, we take x = 9.
Therefore, the value of x is 9.
To learn more about the quadratic equation;
https://brainly.com/question/17177510
#SPJ1
4. a survey was conducted with 420 hotel guest the finding was that 20% of the guests were not happy with the standard of cleanliness in the hotel how many guests were not happy?
Answers
The number of guests that were not happy with the standard of cleanliness in the hotel is given as follows:
84 guests.
How to obtain the number of guests?The number of guests that were not happy with the standard of cleanliness in the hotel is obtained applying the proportions in the context of the problem.
The parameters for the problem are given as follows:
Total of 420 guests.Of those, 20% = 0.2 were not happy.Hence the number of guests that were not happy with the standard of cleanliness in the hotel is given as follows:
420 x 0.2 = 84 guests.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Jon is solving this division problem: 7,846 : 3. In what place should he start dividing?
thousands
hundreds
ones
tens
answer is ones
Answers
Heeelpppppppp fasttttttttttttt!!!!!!!!!!!!!!!!

Answers
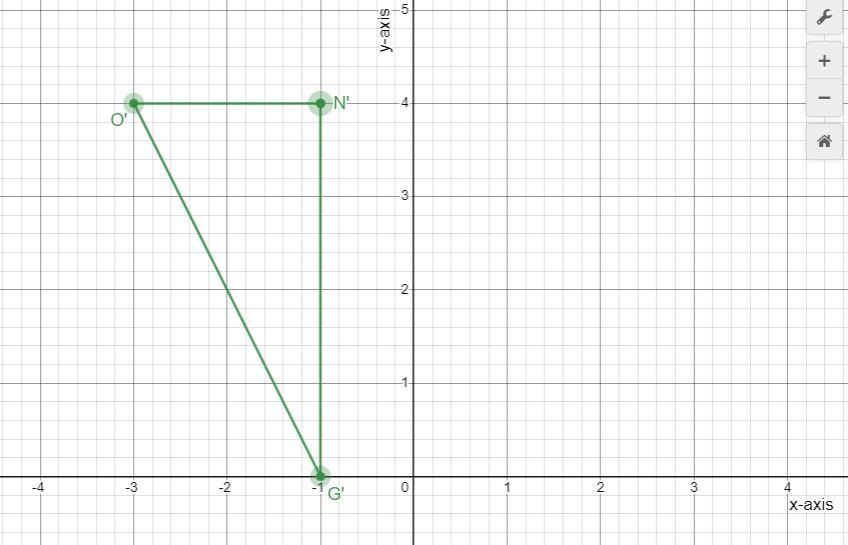
Rotation 90° clockwise about the origin
N
O
G

Answers
An image of triangle NOG after a rotation 90° clockwise about the origin is shown below.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
Next, we would apply a rotation of 90° clockwise about the origin to the coordinate of this triangle NOG in order to determine the coordinate of its image;
(x, y) → (y, -x)
Point N = (-4, -1) → Point N' (-1, 4)
Point O = (-4, -3) → Point O' (-3, 4)
Point G = (0, -1) → Point G' (-1, 0)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
How to tell if a graph is a function in algebra
Answers
Answer:
Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
Step-by-step explanation:
If there is any such line, the graph does not represent a function. If no vertical line can intersect the curve more than once, the graph does represent a function.
Can someone watch number 10 ?

Answers
Answer:
-9
Step-by-step explanation:
Hello! So, we need to find log_6 1/6. The definition of log is the power that you need to multiply that number by to get the next number. 1/6=6^-1, so our equation would be:
-1=x/9, so x is clearly -9.
Have a nice day.
~cloud
Answer:
You are correct
Step-by-step explanation:
\(log_{6} \frac{1}{6} =\frac{x}{9}\)
\(log_{6} 6^{-1} =\frac{x}{9}\)
\((-1)log_{6}6=\frac{x}{9}\)
\(-1=x/9\)
\(-9=x\)
Hope that helps :)
\( \displaystyle \rm\lim_{n \to \infty } \sqrt[n]{ \left( \sum_{k = 1}^{n} \frac{ {k}^{2} }{ {2k}^{2} - 2nk + {n}^{2} } \right) \left( \sum_{k = 1}^{n} \frac{ {k}^3}{ {3k}^{2} - 3nk + {n}^{2} } \right)} \)
Answers
Rewrite the sums as
\(\displaystyle S_2 = \sum_{k=1}^n \frac{k^2}{2k^2 - 2nk + n^2} = \sum_{k=1}^n \frac{\frac{k^2}{n^2}}{\frac{2k^2}{n^2} - \frac{2k}n + 1}\)
and
\(\displaystyle S_3 = \sum_{k=1}^n \frac{k^2}{3k^2 - 3nk + n^2} = \sum_{k=1}^n \frac{\frac{k^2}{n^2}}{\frac{3k^2}{n^2} - \frac{3k}n + 1}\)
Now notice that
\(\displaystyle \lim_{n\to\infty} \frac{S_2}n = \int_0^1 \frac{x^2}{2x^2 - 2x + 1} = \frac12\)
and
\(\displaystyle \lim_{n\to\infty} \frac{S_3}n = \int_0^1 \frac{x^2}{3x^2 - 3x + 1} = \frac{9 + 2\pi\sqrt3}{27}\)
and the important point here is that \(\frac{S_2}n\) and \(\frac{S_3}n\) converge to constants. For any real constant a, we have
\(\displaystyle \lim_{n\to\infty} \frac{\ln(an)}n = 0\)
Rewrite the limit as
\(\displaystyle \lim_{n\to\infty} \sqrt[n]{S_2 \times S_3} = \lim_{n\to\infty} \exp\left(\ln\left(\sqrt[n]{S_2 \times S_3}\right)\right) \\\\ = \exp\left(\lim_{n\to\infty} \frac{\ln(S_2) + \ln(S_3)}n\right) \\\\ = \exp\left(\lim_{n\to\infty} \frac{\ln\left(n \times \frac{S_2}n\right) + \ln\left(n \times \frac{S_3}n\right)}n\right)\)
Then
\(\displaystyle \lim_{n\to\infty} \sqrt[n]{S_2 \times S_3} = e^0 = \boxed{1}\)
A plot of the limand for n = first 1000 positive integers suggests the limit is correct, but convergence is slow.
![[tex] \displaystyle \rm\lim_{n \to \infty } \sqrt[n]{ \left( \sum_{k = 1}^{n} \frac{ {k}^{2} }{ {2k}^{2}](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/25skdWe02MnK6N3lm7xSvCiCK42Q18Ks.png)
at a baseball game a vender sold a combined total of 141 sodas and hot dogs. the number of sodas was 51 more than the number of hotdogs sold. Find the number of sodas sold and the number of hot dogs sold
Answers
Hot Dogs: 45
find the standard deviation of 3, 21, 21.4, 17.4, 12.6, 2.6, 11.2, 16.9
Answers
Answer:
Standard Deviation: 6.8932825090809
Step-by-step explanation:
Sum: 106.1
Standard Deviation: 6.8932825090809
Mean: 13.2625
Count: 8
Range: 18.8
Median: 14.75
(Hope this helps can I pls have brainlist (crown)☺️)
T/F. victor found 5 cars online that he will go to see. the prices of the cars are: $5,000; $4,500; $5,500; $3,999; and $4,999. the median car price is $4,799.60.
Answers
False
The median car price is the one right in the middle of the price list. To find the median, we first need to rank the prices from lowest to highest.
The ordered price list looks like this:
$3,999; $4,500; $4,999; $5,000; The median price is $4,999, which is the median price. The average price is not $4,799.60.
Median is a measure of the central tendency of a dataset. The value that separates the top and bottom halves of the record. To find the median, we need to enter the values in the dataset in order from lowest to highest. If the dataset has an odd number of values, the median is the mean.
For example, given the following five values: For 3, 5, 7, 9, 11, the median is the median, so the median is 7. If the dataset has an even number of values, the median is the average of the two middle values. For example, given the following 6 values:
For 3, 5, 7, 9, 11, 13, the median is (7 + 9)/2 = 8. In this case, there are 5 values, which are odd, so the median is the median. , which is $4,999.
Read more about this on brainly.com/question/16688394
#SPJ4
I keep getting the wrong answer.

Answers
The volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis is 51π cubic units.
What is the volume of the solid obtained by rotating the region in the first quadrant bounded by the given curve about the y - axis?To find the volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis, we can use the method of cylindrical shells.
The formula for the volume using cylindrical shells is:
V = 2π ∫ [a, b] x * h(x) dx
Where:
- V is the volume of the solid
- π represents the mathematical constant pi
- [a, b] is the interval over which we are integrating
- x is the variable representing the x-axis
- h(x) is the height of the cylindrical shell at a given x-value
In this case, we need to solve for x in terms of y to express the equation in terms of y.
Rearranging the given equation:
x = 5 ± √(1 - y)
Since we are only interested in the region in the first quadrant, we take the positive square root:
x = 5 + √(1 - y)
Now we can rewrite the volume formula with respect to y:
V = 2π ∫ [c, d] x * h(y) dy
Where:
- [c, d] is the interval of y-values that correspond to the region in the first quadrant
To determine the interval [c, d], we set the equation equal to zero and solve for y:
1 - (x - 5)² = 0
Expanding and rearranging the equation:
(x - 5)² = 1
x - 5 = ±√1
x = 5 ± 1
Since we are only interested in the region in the first quadrant, we take the value x = 6:
x = 6
Now we can evaluate the integral to find the volume:
V = 2π ∫ [0, 1] x * h(y) dy
Where h(y) represents the height of the cylindrical shell at a given y-value.
Integrating the expression:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * h(y) dy
To find h(y), we need to determine the distance between the y-axis and the curve at a given y-value. Since the curve is symmetric, h(y) is simply the x-coordinate at that point:
h(y) = 5 + √(1 - y)
Substituting this expression back into the integral:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
Now, we can evaluate this integral to find the volume
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
To simplify the integral, let's expand the expression:
V = 2π ∫ [0, 1] (25 + 10√(1 - y) + 1 - y) dy
V = 2π ∫ [0, 1] (26 + 10√(1 - y) - y) dy
Now, let's integrate term by term:
\(V = 2\pi [26y + 10/3 * (1 - y)^\frac{3}{2} - 1/2 * y^2]\)] evaluated from 0 to 1
V = \(2\pi [(26 + 10/3 * (1 - 1)^\frac{3}{2} - 1/2 * 1^2) - (26 * 0 + 10/3 * (1 - 0)^\frac{3}{2} - 1/2 * 0^2)]\)
V = 2π [(26 + 0 - 1/2) - (0 + 10/3 - 0)]
V = 2π (25.5)
V = 51π cubic units
Learn more on volume of a solid obtained by rotating curve here;
https://brainly.com/question/32301706
#SPJ1
giving 10 brainlist to whoever gets it RIGHT

Answers
Answer:
.001276
Step-by-step explanation:
127.6 ÷ 10^5
Dividing by 10^5 means we are moving the decimal 5 places to the left
We need to add zeros in front of the number to move it to the left
00127.6
Now move it 5 places
.001276
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
what is the total surface area?

Answers
= 1/2 x 9 x 4 = 18
18 x 4 = 72
72 + 9 x 9 = 153m^2
what type of object around in locality
Answers
Objects commonly found in a locality include residential buildings, commercial establishments, public facilities, transportation infrastructure, landmarks, natural features, utilities, street furniture, and vehicles.
The type of objects that can be found in a locality can vary greatly depending on the specific location and its surroundings. Here are some common types of objects that can be found in a locality:
Residential Buildings: Houses, apartments, condominiums, and other types of residential structures are commonly found in localities where people live.
Commercial Establishments: Localities often have various types of commercial establishments such as stores, shops, restaurants, cafes, banks, offices, and shopping centers.
Public Facilities: Localities typically have public facilities such as schools, libraries, hospitals, community centers, parks, playgrounds, and sports facilities.
Transportation Infrastructure: Localities usually have roads, sidewalks, bridges, and public transportation systems like bus stops or train stations.
Landmarks and Monuments: Some localities may have landmarks, historical sites, monuments, or cultural attractions that represent the area's heritage or significance.
Natural Features: Depending on the locality's geographical characteristics, natural features like parks, lakes, rivers, mountains, forests, or beaches can be present.
Utilities: Localities have infrastructure for utilities such as water supply systems, electrical grids, sewage systems, and telecommunications networks.
Street Furniture: Localities often have street furniture like benches, streetlights, waste bins, traffic signs, and public art installations.
Vehicles: Various types of vehicles can be found in a locality, including cars, bicycles, motorcycles, buses, trucks, and possibly other modes of transportation.
It's important to note that the objects present in a locality can significantly differ based on factors such as urban or rural setting, cultural context, economic development, and geographical location.
for such more question on public facilities
https://brainly.com/question/25380567
#SPJ8
write the equation of the line that goes through points (1, 1) and (3, 7)
Answers
Given the points:
(x1, y1) ==> (1, 1)
(x2, y2) ==> (3, 7)
To find an equation of the line that goes through the points, first find the slope using the slope formula below:
\(m=\frac{y2-y1}{x2-x1}\)Substitue values into the formula and solve for the slope, m:
\(\begin{gathered} m=\frac{7-1}{3-1} \\ \\ m=\frac{6}{2} \\ \\ m=3 \end{gathered}\)The slope of the line, m is = 3.
Now, use the point slope form:
(y - y1) = m(x - x1)
Substitute 1 for y1, 1 for x1, and 3 for m:
(y - 1) = 3(x - 1)
Let's rewrite the equation to slope intercept form: y = mx + b
Where m is the slope and b is the y-intercept
y - 1 = 3(x) + 3(-1)
y - 1 = 3x - 3
Add 1 to both sides:
y - 1 + 1 = 3x - 3 + 1
y + 0 = 3x - 2
y = 3x - 2
Therefore, the equation of the line in slope intercept form is:
y = 3x - 2
ANSWER:
y = 3x - 2
