How do you find the reflecting on a coordinate plane( x-axis or y-axis )?
Answers
A transformative process turns a figure into a reflection.
How do you determine the reflecting on an x-axis or y-axis coordinate plane?If you want to reflect a point across the x-axis, multiply its y-coordinate by -1. If you want to reflect a point across the y-axis, multiply its x-coordinate by -1.A transformative process turns a figure into a reflection.When a point is reflected across the x-axis, the x-coordinate stays constant, but the y-coordinate is thought to be the additive inverse. The x-axis shows a reflection of the point (x, y) as (x, -y).The y-coordinate remains constant when a point is mirrored across the y-axis, while the x-coordinate is thought to be the additive inverse. The point (x, y) is reflected on the y-axis as (-x, y).(x, y)(x, y) is the formula for a reflection over the x-axis.
(x,y)(x,y) is the formula for a reflection across the y-axis.
The formula is (x,y)(y,x) for a reflection in the line y=x.
(x, y)(y, x) is the formula for a reflection in the origin.
To learn more about the reflecting on a coordinate plane refer to:
https://brainly.com/question/28703749
#SPJ1
Related Questions
Morgan needs to order some new supplies for the restaurant where she works. The restaurant needs at least 650 glasses. There are currently 380 glasses. If each set on sale contains 15 glasses, write and solve an inequality which can be used to determine ss, the number of sets of glasses Morgan could buy for the restaurant to have enough glasses.
Answers
Answer:
43 Sets for 650
Step-by-step explanation:
Just do division.
Hope this helps :-)
Answer:
ok
Step-by-step explanation:
12
2
2
2
2
2
3
Find an equation of the circle that satisfies the stated conditions. (Give your answer in standard notation.) Center at the origin, passing through P(5, −8)
Answers
The equation of the circle that meets the specified requirements is x^2 + y^2 = 89, with the center at the origin and going through P(5, 8).
What is equation?In its most basic form, an equation is a mathematical statement that indicates that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical phrase with two equal sides separated by an equal sign is called an equation. An example of an equation is 4 + 6 = 10.
Here,
The equation of a circle with center at the origin (0,0) and passing through the point (x1,y1) can be found using the distance formula.
The distance between a point (x1, y1) and the origin (0,0) is given by:
sqrt((x1-0)^2 + (y1-0)^2) = sqrt(x1^2 + y1^2)
Let's call the radius of the circle r. We know that the distance between the point (x1,y1) and the origin is equal to r. So, we can set up the equation:
sqrt(x1^2 + y1^2) = r
Substituting the values x1 = 5 and y1 = -8, we have:
sqrt(5^2 + (-8)^2) = r
Solving for r, we get:
r = sqrt(5^2 + (-8)^2) = sqrt(25 + 64) = sqrt(89)
Finally, we can write the equation of the circle in standard form using the center (0,0) and radius r:
(x - 0)^2 + (y - 0)^2 = r^2
x^2 + y^2 = r^2
x^2 + y^2 = 89
The equation of the circle that satisfies the stated conditions that is center at the origin, passing through P(5, −8) is x^2 + y^2 = 89.
To know more about equation,
https://brainly.com/question/2228446
#SPJ4
Please help me! thank you
Suppose an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t)=-16t^2+48t+120. Find the average velocity from t=2 to t=4.
Type your answer as a number with no units.
Answers
The average velocity from t = 2s to t = 4s would be - 48 ft/s.
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.
Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.
Given is that an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t) = - 16t² + 48t + 120.
Average velocity
Average rate of change of velocity with time is called average velocity. Mathematically -
v{avg.} = Δx/Δt .... Eq { 1 }
Δx = x(4) - x(2)
Δx = - 16(4)² + 48(4) + 120 - {- 16(2)² + 48(2) + 120}
Δx = - 96
Δt = 4 - 2 = 2
So -
v{avg.} = Δx/Δt = -96/2 = - 48 ft/s
Therefore, the average velocity from t = 2s to t = 4s would be - 48 ft/s.
To solve more questions on functions, visit the link below-
brainly.com/question/17613163
#SPJ1
Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used. Match the pairs of figures that have the same volume. 3-D shape of a cone is represented. The cone has a radius of 4 units and a height of 12 units. 3-D shape of a rectangular prism is represented. The rectangular prism has a length of 18 units, a width of 6 units, a height of 6 units. 3-D shape of a rectangular prism is represented. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units. 3-D shape of a cylinder is represented. The cylinder has a radius of 3 units and a height of 8 units. 3-D shape of a cone is represented. The cone has a radius of 8 units and a height of 9 units. 3-D shape of a rectangular prism is represented. The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units. arrowBoth 3-D shape of a cylinder is represented. The cylinder has a radius of 4 units and a height of 12 units. arrowBoth 3-D shape of a cone is represented. The cone has a radius of 6 units and a height of 6 units. arrowBoth Reset Next © 2023 Edmentum. All rights reserved.
Answers
The pair of figures having same volume are:
a. The cylinder has a radius of 3 units and a height of 8 units ; The cone has a radius of 6 units and a height of 6 units.
b. The cone has a radius of 8 units and a height of 9 units ; The cylinder has a radius of 4 units and a height of 12 units.
c. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units ; The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units.
What is volume of a figure?
Volume is a unit of measurement for three-dimensional space. It is usually stated quantitatively in terms of a number of imperial or US-standard units as well as SI-derived units.
i. The cone has a radius of 4 units and a height of 12 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(4^{2} \frac{12}{3}\)
⇒ Volume = 64 π
⇒ Volume = 201 cubic units
ii. The rectangular prism has a length of 18 units, a width of 6 units, a height of 6 units.
⇒ Volume = length * width * height
⇒ Volume = 18 * 6 * 6
⇒ Volume = 648 cubic units
iii. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units.
⇒ Volume = length * width * height
⇒ Volume = 16 * 6 * 6
⇒ Volume = 576 cubic units
iv. The cylinder has a radius of 3 units and a height of 8 units.
⇒ Volume = π\(r^{2}\)h
⇒ Volume = π\(3^{2}\) * 8
⇒ Volume = 72 π
⇒ Volume = 226 cubic units
v. The cone has a radius of 8 units and a height of 9 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(8^{2} \frac{9}{3}\)
⇒ Volume = 192 π
⇒ Volume = 603 cubic units
vi. The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units.
⇒ Volume = length * width * height
⇒ Volume = 8 * 8 * 9
⇒ Volume = 576 cubic units
vii. The cylinder has a radius of 4 units and a height of 12 units.
⇒ Volume = π\(r^{2}\)h
⇒ Volume = π\(4^{2}\) * 12
⇒ Volume = 192 π
⇒ Volume = 603 cubic units
viii. The cone has a radius of 6 units and a height of 6 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(6^{2} \frac{6}{3}\)
⇒ Volume = 72 π
⇒ Volume = 226 cubic units
Hence, three pairs have the same volume.
Learn more about volume from the given link
https://brainly.com/question/463363
#SPJ1
The missing figures have been attached below.



A worker wants to save enough money to buy new
headphones, which cost $119. He makes $7 per hour at his
job. He wants to figure out the least number of hours he can
work to have enough money to buy the headphones. Write
an inequality and solve.

Answers
Answer:
The least amount of numbers that he can work at his job to have enough for the headphones he wants is 17 hours.
Step-by-step explanation:
To find the number of hours you could divide the cost of the headphones by the amount he earns each hour so you would do $119/ 7 to get 17 and then you could check your answer with multiplication by multiplying 7 * 17 to get 119 which shows that he has to work at least 17 hours to get the headphones he wants.
$119 / 7 = 17
17 * 7 = 119
What is 800divided by the a times the 9 3 times?
Answers
Answer:
21600/a
Step-by-step explanation:
800/a *9
7200/a
21600/a
First, times 800 divided by a by 9.
Then, we get 7200/a.
Lastly, times it by 3.
The answer is 21600/a
Sussy mcsuser
Poop noobs
Carols den is 8 feet longer than it is wide. If the dens area is 209 square feet what are the dinensions of the room?
Answers
Answer:
12 42
Step-by-step explanation:
Jade has seven cards. Each card is labeled with a letter. A B C D E F G H J Jade picks one of her cards at random. Find the probability that the card she picks is a) labelled F, b) labelled with a letter in her name JADE c) labelled with a letter that has at least one line of symmetry
Answers
Answer:
(a) \(\frac{1}{7}\)
(b) \(\frac{4}{7}\)
(c) \(\frac{5}{7}\)
Step-by-step explanation:
Probability (P) of an event is the likelihood that the event will occur. It is given by;
P = number of favourable outcomes ÷ total number of events in the sample space.
Given letters of cards:
A B C D E F G H J
∴ Total number of events in sample space is actually the number of cards which is 7
If a card is picked at random;
(a) the probability P(F), that it is labelled F is given by;
P(F) = number of favourable outcomes ÷ total number of events in the sample space.
The number of favourable outcomes for picking an F = 1 since there is only one card labelled with F.
∴ P(F) = 1 ÷ 7
=> P(F) = \(\frac{1}{7}\)
(b) the probability P(N), that it is labelled with a letter in her name JADE is given by;
P(N) = P(J) + P(A) + P(D) + P(E)
Where;
P(J) = Probability that it is labelled J
P(A) = Probability that it is labelled A
P(D) = Probability that it is labelled D
P(E) = Probability that it is labelled E
P(J) = \(\frac{1}{7}\)
P(A) = \(\frac{1}{7}\)
P(D) = \(\frac{1}{7}\)
P(E) = \(\frac{1}{7}\)
∴ P(N) = \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\)
∴ P(N) = \(\frac{4}{7}\)
(c) the probability P(S), that it is labelled with a letter that has at least one line of symmetry is;
P(S) = P(A) + P(B) + P(C) + P(D) + P(E) + P(H)
Where;
P(A) = Probability that it is labelled A
P(B) = Probability that it is labelled B
P(C) = Probability that it is labelled C
P(D) = Probability that it is labelled D
P(E) = Probability that it is labelled E
P(H) = Probability that it is labelled H
Cards with letters A, B, C, D, E and H are selected because these letters have at least one line of symmetry. A line of symmetry is a line that cuts an object into two identical halves. Letters A, B, C, D, E and H can each be cut into two identical halves.
P(A) = \(\frac{1}{7}\)
P(B) = \(\frac{1}{7}\)
P(C) = \(\frac{1}{7}\)
P(D) = \(\frac{1}{7}\)
P(E) = \(\frac{1}{7}\)
P(H) = \(\frac{1}{7}\)
∴ P(S) = \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\)
∴ P(S) = \(\frac{5}{7}\)
jack has a square flower bed in his garden with perimeter 120 m, he wants to deconstruct this flower bed and turn it into a triangular flower bed with maximum area. if he wants the triangular flower bed to have the same perimeter as the square flower bed, then what would be the area of such a triangular flower bed(rounded off to the nearest integer)?
Answers
To find the maximum area for the triangular flower bed with the same perimeter as the square flower bed, we can use the concept of an equilateral triangle.
Let's denote the side length of the square flower bed as 's'. Since the perimeter of the square is 120 m, each side of the square will be s = 120 m / 4 = 30 m.
Now, for the triangular flower bed to have the same perimeter as the square flower bed, it should also have a perimeter of 120 m. In an equilateral triangle, all three sides are equal in length.
Let's denote the side length of the equilateral triangle as 't'. Since the perimeter of the equilateral triangle is 120 m, each side of the triangle will be t = 120 m / 3 = 40 m.
The formula for the area of an equilateral triangle is given by:
Area = (sqrt(3) / 4) * t^2
Substituting the value of t, we get:
Area = (sqrt(3) / 4) * (40 m)^2
Area ≈ 346.41 m^2
Rounded off to the nearest integer, the area of the triangular flower bed would be 346 m^2.
The number of baseball games, x, that Karen went to last year is more than 5.
Answers
a city recreation department plans to build a rectangular playground having an area of 16,900 square meters and surround it by a fence. how can this be done using the least amount of fence
Answers
On solving the provided question we can say that - Use a 130 m by 90 m fence for the playground's perimeter to use the least amount of fencing possible.
What is Perimeter?A boundary is a closed route that surrounds, encloses, or defines a one-dimensional length or a two-dimensional form. There are various real-world uses for perimeter calculation.
The playground has a 16900m2 space. We discover the factors of 16900 to get the length and width that may be attainable.
factors are - \(26*650, 1300*13, 130*90 and 65*260\)
The formula for a rectangle's perimeter is 2(l+w).
Dimensions 130 and 90 will provide the least amount of perimeter utilising all these criteria.
\(440 i.e 2(130+90)= 440.\)
Therefore, 130m by 90m is the smallest dimension for fencing the playground.
To know more about perimeter visit:
https://brainly.com/question/6465134
#SPJ4
Circle E is inscribed with triangle B C D. LIne segment B D is a diameter. Line segments D C and C B are secants. Angle D B C is 51 degrees.
What is the measure of arc B C?
39°
78°
102°
129°
Answers
The measure of arc BC in circle E, inscribed in triangle BCD with angle DBC measuring 51 degrees, is 102°.
In a circle, an inscribed angle is equal to half the measure of its intercepted arc. Since BD is a diameter, angle DBC is a right angle, and the intercepted arc BC is a semicircle. Therefore, the measure of arc BC is 180°.
However, we are given that angle DBC measures 51 degrees. In an inscribed triangle, the measure of an angle is equal to half the measure of its intercepted arc. So, angle DBC is half the measure of arc BC, which means arc BC measures 2 times angle DBC, or 2 * 51° = 102°.
Hence, the measure of arc BC is 102°.
Learn more about semicircle here:
https://brainly.com/question/29140521
#SPJ11
Inscribed circle E is formed by triangle BCD, with BD as the diameter. DC and CB are secants, and angle DBC is 51 degrees. We need to find the measure of arc BC.
When a triangle is inscribed in a circle, the measure of an angle formed by two secants that intersect on the circle is half the measure of the intercepted arc.
In this case, angle DBC is 51 degrees, which means the intercepted arc BC has twice that measure. Therefore, the measure of arc BC is 2×51=102 degrees.
To understand why this relationship holds, we can use the Inscribed Angle Theorem. According to this theorem, an angle formed by two chords or secants that intersect on a circle is equal in measure to half the measure of the intercepted arc.
In our scenario, angle DBC is formed by secants DC and CB, and it intersects the circle at arc BC. According to the Inscribed Angle Theorem, angle DBC is equal to half the measure of arc BC.
Hence, if angle DBC is 51 degrees, the measure of arc BC is twice that, which gives us 102 degrees.
Learn more about Inscribed Angle Theorem here:
https://brainly.com/question/5436956
#SPJ11
Resuelve el siguiente sistemas de ecuaciones por el método
de sustitución
83x - 20y = 590
60x + 18y = 816
Answers
Answer:
x=10 and y=12
Step-by-step explanation:
To solve this quadratic equation we will use two method
1. Elimination method
2. substitution method
first of we use elimination method
we either eliminate x or y
we will be eliminating y
83x-20y=590..........(eq1)
60x+18y=816...........(eq2)
y will be eliminated by multiplying
(eq1) by 9
(eq2) by 10
which will give
747x-180y=5310.........(eq3)
600x-180y=8160.........(eq4)
see that y has the same value that is (-180y and +180y)
so to eliminate y completely you have to add eq1 and eq2 because if you don't add them together you wont eliminate y
747x-180y=5310
+
600x+180y=8160
=
1347x+0=13470
1347x=13470
x=13470/1347
x=10
Now to find y we use substitution method ie put x=10 in any of the equation above(eq1,eq2,eq3, eq4) you will get the same answer
eq1
83x-20y=590..... where (x=10)
83(10)-20y =590
830-20y=590
like terms
-20y=590-830
-20y= -240
divide both sides with -20
y= -240/-20
y=12
OR
eq2
60x+18y=816..... where x=10
60(10)+18y=816
600+18y=816
like term
18y=816-600
18y=216
y=216/18
y= 12
or eq3 or eq4 you will still get the same answer......
La solución del sistema es:
x = 10y = 12En el sistema:
83×x - 20×y = 590
60×x + 18×y = 816
Se puede, de manera de facilitar las operaciones matemáticas simplificar la segunda ecuación, dividiendo por 6
60/6 ×x + 18/6 ×y = 816/6 ⇒ para obtener 10×x + 3×y = 136
Entonces el sistema es ahora:
83×x - 20×y = 590 (1)
10×x + 3×y = 136 (2)
El método de sustitución consiste en:
De una de las ecuaciones se despeja una incognita ( en nuestro caso despejaremos x de la segunda ecuación)El valor obtenido se sustituye en la otra ecuación ( en este caso en la primera ecuación)Se obtiene así una ecuación en la otra variable, se resuelve esa ecuación, y posteriormente se sustituye en el valor obtenido en el primer pasoEntonces:
10×x + 3×y = 136 despejando x
x = (136 - 3×y)/10 (3)
Sustituyendo en ecuación (2)
83× [(136 - 3×y)/10] - 20×y = 590
Resolviendo
(11288 - 249×y )/ 10 - 20×y = 590
11288 - 249×y - 20×10×y = 590×10
11288 - 449×y - 200×y = 5900
- 449×y = -5388
y = 12
LLevando este valor a la relación(3)
x = (136 -3×12)/10
x = 100/100
x = 10
can i get some help on this question?

Answers
68/8.5 = 8
So b = 8
Bye I hope this helps you pass!

1. You are building a porch that
has a perimeter of 28 ft. If the
width of the porch is four less
than the length find the length of
the porch?
Answers
Answer:
2
Step-by-step explanation:
because i don't know okay
Answer:
9 ft.
Step-by-step explanation:
1.
If there are 2 sides for width and 2 sides for length, you would need to add the difference from both the sides of length which would be 8.
2.
28 - 8 = 20.
So if all the sides were equal, each one would be 5 ft.
If the each length side is 4 more than the width sides, you would add 4 to 5 so each length side is 9. So the length of the porch is 9 ft.
The sum of the ages of a father and son is 56. Four years ago the father was 3 times as old as the son. Find the present age of each.
Answers
Answer:
Son is 16
father is 40
Step-by-step explanation:
Determine which integers in the set S: {−2, −3, −4, −5} will make the inequality 3p − 10 ≥ 7p + 6 true.
Answers
The integers in the solution set of 3p − 10 ≥ 7p + 6 are -4 and -5
What are inequality expressions?Inequality expressions are mathematical statements that are represented by variables, coefficients and operators where the opposite sides are not equal
How to determine the integers in the set?The set is given as
S: {−2, −3, −4, −5}
The inequality expression is given as
3p − 10 ≥ 7p + 6
We start by evaluating the inequality expression
So, we have
3p − 10 ≥ 7p + 6
Subtract 7p from both sides of the inequality expression
So, we have
-4p − 10 ≥ 6
Add 10 to both sides of the inequality expression
So, we have
-4p ≥ 16
Divide both sides of the inequality expression hy -4
So, we have
p ≤ -4
This means that the integers in the solution set are integers that do not exceed -4
These integers are -4 and -5
Hence, the solution is -4 and -5
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1
Hi yall i'll be giving away brainlist for best answer
please view the image to get a better understanding on it :(( appreciate it

Answers
The rate of change is 4.
Equation: y=4x+6
Thanks for requesting me to answer! I am not sure what the difference between pattern and rate of change is but I hope this helps.
Suppose the probability of event A is 0.40 and the probability of event Bis 0.28. If events A and B are independent, then P(A or B) is: a. 0.68 b. 0.1120 c. 0.5680 d. 0
Answers
The probability of event A or B occurring (P(A or B)) is 0.5680, which corresponds to option c. To solve this problem, we can use the formula:
P(A or B) = P(A) + P(B) - P(A and B)
Since events A and B are independent, we know that P(A and B) = P(A) * P(B)
Substituting the given probabilities, we get:
P(A or B) = 0.40 + 0.28 - (0.40 * 0.28)
P(A or B) = 0.68 - 0.112
P(A or B) = 0.568
Therefore, the answer is c. 0.5680.
If events A and B are independent, we can find the probability of A or B occurring (P(A or B)) by using the formula: P(A or B) = P(A) + P(B) - P(A) * P(B).
Given the probability of event A (P(A)) is 0.40 and the probability of event B (P(B)) is 0.28, we can plug these values into the formula:
P(A or B) = 0.40 + 0.28 - (0.40 * 0.28) = 0.40 + 0.28 - 0.112 = 0.568.
So, the probability of event A or B occurring (P(A or B)) is 0.5680, which corresponds to option c.
Visit here to learn more about probability brainly.com/question/30034780
#SPJ11
Solve the triangles. Round decimal answers to the nearest tenth.


Answers
The measurements are 1) ∠B = 65°, a = 23.78 and b = 32.22 and 2) ∠B = 66°, a = 14.33 and b = 24.04
1) Given is a triangle ABC we need to find the missing measures,
So, using the angle sum property of a triangle we get,
∠B = 180° - (73° + 42°)
∠B = 65°
Now we will use the Sine law to find the missing sides,
Sin A / a = Sin B / b = Sin C / c
So,
Sin 42° / a = Sin 73° / 34
Sin 42° × 34 / Sin 73° = a
a = 23.78
Similarly,
b = Sin 65° × 34 / Sin 73°
b = 32.22
So, ∠B = 65°, a = 23.78 and b = 32.22
Similarly part 2 can be solved.
Hence the measurements are 1) ∠B = 65°, a = 23.78 and b = 32.22 and 2) ∠B = 66°, a = 14.33 and b = 24.04
Learn more about Sine law click;
https://brainly.com/question/13098194
#SPJ1
I wanna know whats 10+-5 and worked out
Answers
Answer:
5
Step-by-step explanation:
Replace all occurrences of + - with a single -. A plus sign followed by a minus sign has the same mathematical meaning as a single minus sign because
1 * -1 = -1
10 - 5
Subtract.
10
- 5
___
5
if an independent event has four uncertain outcomes, their probabilities are 20%, 45%, 15%, and a. 10%. b. 15%. c. 20%. d. 25%. e. 30%.
Answers
If an independent event has four uncertain outcomes, their probabilities are 20%, 45%, 15%, and C: 20%.
In probability, the sum of the probabilities of all possible outcomes must equal 100%. In this case, the probabilities of the four uncertain outcomes are given as 20%, 45%, 15%, and 20%. This means that each of these outcomes has a chance of occurring equal to the given percentage, and the total probability of all four outcomes is 20% + 45% + 15% + 20% = 100%.
It is important to note that when calculating probabilities, the percentages must add up to 100% to ensure that the total chance of all possible outcomes occurring is equal to 1 or 100%.
You can learn more about probability at
brainly.com/question/24756209
#SPJ4
Which system of equations has no solutions?
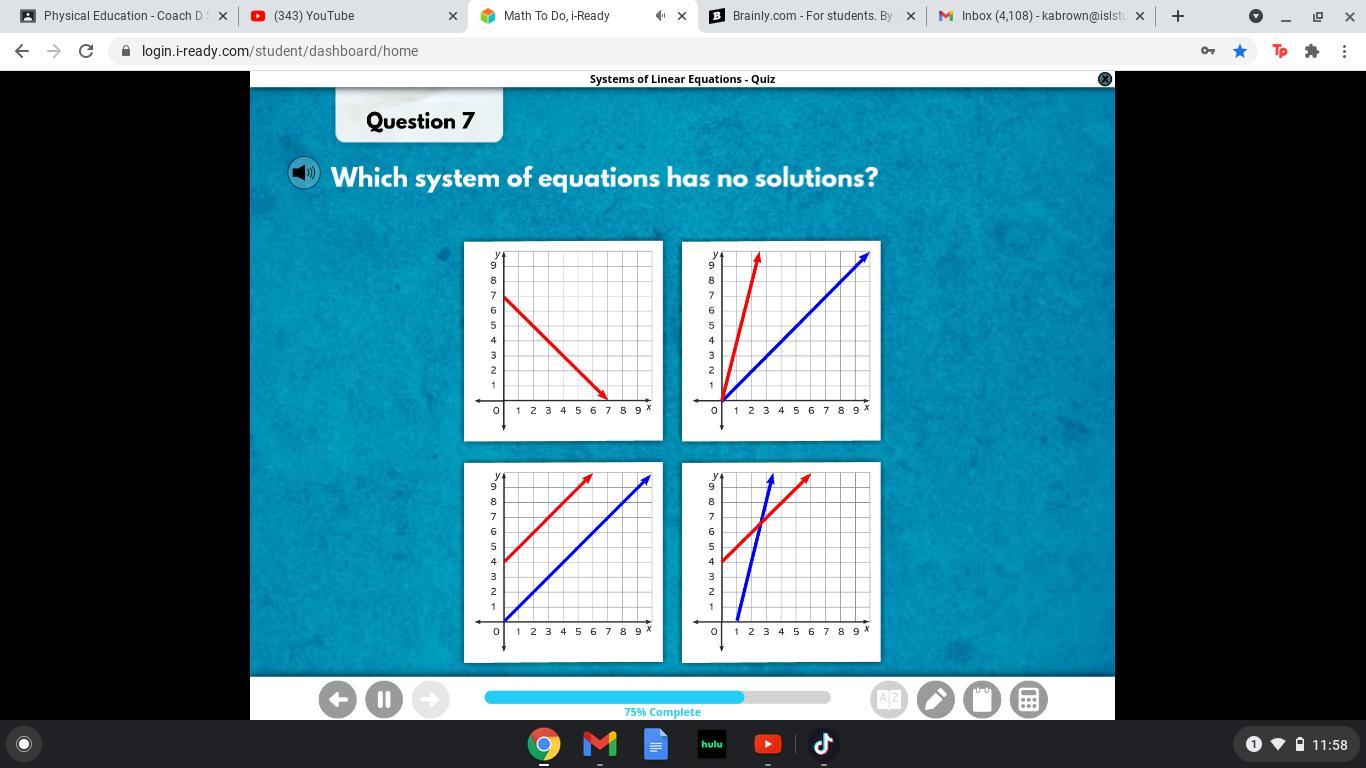
Answers
Answer:
a
Step-by-step explanation:
why do i think it is well if u put the graph bar on googl and then u will no
f(x)=log5x what Is the range of the function
Answers
The range of the function f(x) = log5x is (-∞, +∞).The function f(x) = log5x represents the logarithm base 5 of x. To determine the range of this function, we need to consider the possible values that the logarithm can take.
The range of the logarithm function y = log5x consists of all real numbers. The logarithm function is defined for positive real numbers, and as x approaches 0 from the positive side, the logarithm approaches negative infinity. As x increases, the logarithm function approaches positive infinity.
The range of the function is the set of all possible output values. In this case, the range consists of all real numbers that can be obtained by evaluating the logarithm
log5(�)log 5 (x) for �>0 x>0.
Since the base of the logarithm is 5, the function log5x will take on all real values from negative infinity to positive infinity. Therefore, the range of the function f(x) = log5x is (-∞, +∞).
In other words, the function can output any real number, ranging from negative infinity to positive infinity. It does not have any restrictions on the possible values of its output.
For more such questions on Logarithm:
https://brainly.com/question/31117877
#SPJ8
Answer: All real numbers
Step-by-step explanation:
Edge
8x – 2 > -18
Can someone let me know if I am correct ?

Answers
Answer:
x > -2
Step-by-step explanation:
Add 2 to both sides
8x >= -16
Divided both sides by 8
x >= -2
Your answer is correct but on the number line the graph should be the other way to the right
•——————>
-2
Hope it helps
Please help me with this question will mark brainlist

Answers
Answer: X is 35, the angle is 75°
Step-by-step explanation:
(2x + 5) + 3x =180
They are supplementary angles, which the sum of them are 180.
2x + 5 + 3x = 180
5x + 5 = 180
5x = 175
x = 35
∠ABC = 2X + 5 = 2(35) + 5 = 70 + 5 = 75°
Find the circumference of the circle. Then, find the length of each bolded arc. Use appropriate notation

Answers
Answer:
\(\text{1) }\\\text{Circumference: }24\pi \text{ m}},\\\text{Length of bolded arc: }18\pi \text{ m}\\\\\text{3)}\\\text{Circumference. }4\pi \text{ mi},\\\text{Length of bolded arc: } \frac{3\pi}{2}\text{ mi}\)
Step-by-step explanation:
The circumference of a circle with radius \(r\) is given by \(C=2\pi r\). The length of an arc is makes up part of this circumference, and is directly proportion to the central angle of the arc. Since there are 360 degrees in a circle, the length of an arc with central angle \(\theta^{\circ}\) is equal to \(2\pi r\cdot \frac{\theta}{360}\).
Formulas at a glance:
Circumference of a circle with radius \(r\): \(C=2\pi r\) Length of an arc with central angle \(\theta^{\circ}\): \(\ell_{arc}=2\pi r\cdot \frac{\theta}{360}\)Question 1:
The radius of the circle is 12 m. Therefore, the circumference is:
\(C=2\pi r,\\C=2(\pi)(12)=\boxed{24\pi\text{ m}}\)
The measure of the central angle of the bolded arc is 270 degrees. Therefore, the measure of the bolded arc is equal to:
\(\ell_{arc}=24\pi \cdot \frac{270}{360},\\\\\ell_{arc}=24\pi \cdot \frac{3}{4},\\\\\ell_{arc}=\boxed{18\pi\text{ m}}\)
Question 2:
In the circle shown, the radius is marked as 2 miles. Substituting \(r=2\) into our circumference formula, we get:
\(C=2(\pi)(2),\\C=\boxed{4\pi\text{ mi}}\)
The measure of the central angle of the bolded arc is 135 degrees. Its length must then be:
\(\ell_{arc}=4\pi \cdot \frac{135}{360},\\\ell_{arc}=1.5\pi=\boxed{\frac{3\pi}{2}\text{ mi}}\)
4
∫ (1-e^-x0 dx
0
solve the given equation using the composite simpson’s 1/3 rule with n = 4, and determine the true percent relative error based on the analytical solution. (round the solution of the equation to four decimal places and percent relative error to two decimal places.) The solution of the given equation is with a true percent relative error of Skipped Hint References
Answers
The solution of the given equation is [solution] with a true percent relative error of [error].
What is the numerical solution and true percent relative error?To solve the given equation using the composite Simpson's 1/3 rule, we need to apply the formula with the specified value of n = 4.
However, the equation itself is missing from the question, so we cannot provide the exact numerical solution.
Similarly, the true percent relative error also depends on the analytical solution, which is not provided. Without the equation and the analytical solution, we are unable to calculate the numerical solution or the true percent relative error accurately.
Learn more about composite Simpson's 1/3 rule
brainly.com/question/31987583
#SPJ11
Match the ratios for sin X cos x and tan X

Answers
Answer:
Step-by-step explanation:

The trigonometric function gives the ratio of different sides of a right-angle triangle.
What are Trigonometric functions?The trigonometric function gives the ratio of different sides of a right-angle triangle.
\(\rm Sin \theta=\dfrac{Perpendicular}{Hypotenuse}\\\\\\Cos \theta=\dfrac{Base}{Hypotenuse}\\\\\\Tan \theta=\dfrac{Perpendicular}{Base}\\\\\\Cosec \theta=\dfrac{Hypotenuse}{Perpendicular}\\\\\\Sec \theta=\dfrac{Hypotenuse}{Base}\\\\\\Cot \theta=\dfrac{Base}{Perpendicular}\\\\\\\)
where perpendicular is the side of the triangle which is opposite to the angle, and the hypotenuse is the longest side of the triangle which is opposite the 90° angle.
Given for ∠X, the base side is 7, the perpendicular side is 4√2, while the hypotenuse side is 9. Therefore, the value of the trigonometric ratios are:
\(\rm Sin X=\dfrac{4\sqrt2}{9}\\\\\\Cos X=\dfrac{7}{9}\\\\\\tan X=\dfrac{4\sqrt2}{7}\)
Learn more about Trigonometric functions:
https://brainly.com/question/6904750
#SPJ2
Find the product: (1.2) · (0.11)
Answers
Answer:
The answer is 0.132
Step-by-step explanation:
12/10*11/100
132/1000
=0.132