= Homework: Ch 5.5 HW
Write the equation in standard form using integers.
y = 4x +7
The equation in standard form is
Answers
y = 4x + 7
Move the 4x to the other side with a negative sign
-4x + y = 7
We can’t have the coefficient of x be negative, so multiply the whole equation by -1
So, the standard form is 4x - y = -7
Related Questions
Which statements (more than one) describe the equation 3 x 9 = 27?
3 is 27 times as many as 9.
27 is 9 times as many as 3.
9 times as many as 3 is 27.
9 times as many as 27 is 3.
3 is 9 times as many as 27
Answers
Answer:
9 times as many as 3 is 27.
Step-by-step explanation:
D Question 12 15 pts A condition X is not a necessary condition for Yif: X is absent when Y is present. X and Y are absent together X and Y are present together. X is absolute but Y is relative. X is present when Y is absent. D Question 13 15 pts The controlled experiment in science is most closely related to which of Mill's methods? The method of residues The joint method of agreement and difference. The method of concomitant variation. The method of agreement The method of difference
Answers
Condition X is not a necessary condition for Y.
If X is absent when Y is present, it can be said that X is not required for Y to be present. X and Y are not connected in such a way that the absence of one would lead to the absence of the other. Therefore, X and Y are not necessary for each other.X and Y are absent togetherIf both X and Y are absent, there is no connection between them. Therefore, the absence of one does not lead to the absence of the other. X and Y are not necessary for each other.
X and Y are present together
If X and Y are present together, it does not imply that they are necessary for each other. It could be that there is a third factor, Z, that is required for both X and Y to be present.X is absolute but Y is relativeX is an absolute condition, which means that it is essential for the occurrence of an event. Y, on the other hand, is a relative condition, which means that it may or may not occur.
Therefore, Y is not a necessary condition for X to occur.
If X is present when Y is absent
It can be said that X is not required for Y to be present. X and Y are not connected in such a way that the absence of one would lead to the absence of the other. Therefore, X and Y are not necessary for each other.The controlled experiment in science is most closely related to the method of concomitant variation. In this method, a factor that is suspected to have a causal relationship with the dependent variable is varied and observed to see if there is a corresponding change in the dependent variable.
The controlled experiment involves manipulating the independent variable while keeping all other variables constant to see the effect on the dependent variable. This method is used to establish causality in scientific research and is commonly used in fields such as psychology, medicine, and biology. Therefore, the controlled experiment in science is most closely related to the method of concomitant variation.
To know more about variable visit:
https://brainly.com/question/15078630
#SPJ11
Question 13
A train runs 68m, 127m, 208m, 312m, and 535m in five successive minutes after it
starts. For the next five minutes, it runs an average speed of 33 km/h. Find the
total distance covered in ten minutes,
A. 12 km
B. 10 km
C. 4 km
D. none
Answers
Answer:
C
Step-by-step explanation:
Here in this question , we are interested in calculating the total distance covered by the train in the 10 minutes that it ran.
From the first part of the question, we already know the distances in the first 5 minutes.
Now, to calculate the total distance in the second 5 minutes, we use the distance formula since we have the average speed and the time;
Mathematically; Total distance = average speed * time
From the question, average speed is 33km/h, while time is 5 minutes. To achieve a consistent unit, we convert 5 minutes to hours.
That would be 5/60 = 1/12 hours
So the total distance in the second 5 minutes is;
33 * 1/12 = 2.75 km
Now, to calculate the total distance traveled, let’s add up the distances in the first 5 minutes and convert to kilometers;
That would be;
68 + 127 + 208 + 312 + 535 = 1,250 m
Let’s convert this to km.
We simply divide by 1000 = 1250/1000 = 1.25 km
The total distance is thus ;
1.25 + 2.75 = 4 km
Evaluate the following expression:
30 = 5(8 – 6 + 1) - (2^2 - 3)^3
Answers
Answer:
30=15
Step-by-step explanation:
30=40-30+6-4-27
30=10+2-27
40=12-27
30=-15
Mr. Hernandez combines 1 gallon of orange juice, 3 pints of pineapple juice, and 2 quarts of lemon‐lime soda to make punch for a party. He allows 2 cups of punch for each guest. Will there be enough punch to serve all 14 guests? How much, if any, punch will be left?
Answers
Answer:
In total there are 30 cups and there are 2 left over
Step-by-step explanation:
The first thing is to clarify the equivalences, we have to:
1 gallon = 4 quarts
1 quart = 2 pints
1 pint = 2 cups
We will pass everything to cups,
1 gallon of orange juice = 16 cups
3 pints of pineapple juice = 6 cups
2 quarts of lemon ‐ lime soda = 8 cups
So in total they would be 16 + 6 + 8 = 30 cups
How to get 2 cups for 14 guests in total would be 28 cups, which means that if 2 cups are left and left over.
a machine that is programmed to package 1.60 pounds of cereal is being tested for its accuracy in a sample of 40 cereal boxes, the sample mean filling weight is calculated as 1.62 pounds. the population standard deviation is known to be 0.06 pounds. find the 95% confidence interval for the mean.
Answers
The 95% confidence interval for the mean is (1.6048, 1.6352).Hence, option (d) is the correct answer.
As given, a machine that is programmed to package 1.60 pounds of cereal is being tested for its accuracy in a sample of 40 cereal boxes, the sample mean filling weight is calculated as 1.62 pounds. The population standard deviation is known to be 0.06 pounds. We are required to find the 95% confidence interval for the mean. Here are the steps to solve this problem:
The formula to find the confidence interval is as follows;
Lower limit = x - zα/2 (σ/√n)
Upper limit = x + zα/2 (σ/√n)
Where,
x= sample mean
zα/2 = z-value of the level of significance
σ = population standard deviation
n = sample size
We are given;
x = 1.62 pounds
σ = 0.06 pounds
n = 40
We need to find the z-value of the level of significance, which can be found using the z-table or by using the calculator.Using the z-table, we get the z-value at 95% confidence interval as zα/2 = 1.96
Substituting the values, we get
Lower limit = 1.62 - 1.96(0.06/√40)
Upper limit = 1.62 + 1.96(0.06/√40)
Lower limit = 1.6048, Upper limit = 1.6352
for more questions on confidence interval
https://brainly.com/question/20873848
#SPJ11
Write the following equation in standard form.
y=-3/7x-3
Answers
\(y = - \frac{3}{7}x - 3 \\ \)
Multiply sides by 7
\(7y = - 3x - 21\)
Plus sides 3x
\(3x + 7y = 3x - 3x - 21\)
\(3x + 7y = - 21\)
_________________________________
And we're done.....♥️♥️♥️♥️♥️
When mutex lock is implemented as a binary semaphore, what should its value be initialized to be?
a) 0
b) 1
c) -1
d) none of the above
Answers
Write t+4/t+5 and 9/t-1 with a common denominator
Answers
The sum of t+4/t+5 and 9/t-1 with a common denominator is (t²+12t+41)/[(t+5)(t-1)].
To find a common denominator for the given expressions t+4/t+5 and 9/t-1, we need to determine the least common multiple (LCM) of the denominators (t+5) and (t-1):
The prime factorization of t+5 is (t+5).
The prime factorization of t-1 is (t-1).
Therefore, the LCM is (t+5)(t-1).
To convert t+4/t+5 into an equivalent fraction with the denominator (t+5)(t-1), we multiply both the numerator and denominator by (t-1):
t+4/t+5 = (t+4)(t-1)/[(t+5)(t-1)] = (t²+3t-4)/[(t+5)(t-1)]
To convert 9/t-1 into an equivalent fraction with the denominator (t+5)(t-1), we multiply both the numerator and denominator by (t+5):
9/t-1 = 9(t+5)/[(t+5)(t-1)] = (9t+45)/[(t+5)(t-1)]
Now both fractions have the same denominator, so we can add them:
(t²+3t-4)/[(t+5)(t-1)] + (9t+45)/[(t+5)(t-1)] = (t²+3t-4+9t+45)/[(t+5)(t-1)]
Simplifying the numerator gives:
t²+12t+41
Learn more about the denominator at
https://brainly.com/question/29775115
#SPJ4
CAN YOU HELP ME FAST!!! ( It's about y - intercept)

Answers
Answer:
its (5/2)x
Step-by-step explanation:
(hint: y=mx+b, "m" is the slope)
Hope this helps
Answer:
5/2
Step-by-step explanation:
C. what does it mean when an element is written inside a circle? at the intersection of two circles? outside the circles
D. do the elements written at the intersection of both circles from a subset of the two sets? Why?
Answers
Answer:
c ) it either shows diameter or radius
d) I am not sure
C. When elements are represented in a Venn diagram (using circles), the placement of elements inside or outside the circles indicates their relationship to the sets being represented.
D. Yes, the elements written at the intersection of both circles form a subset of the two sets.
C. Place an element inside a circle to indicate that it is a member of the set indicated by the circle.
An element that is positioned at the intersection of two circles denotes an element that is a part of both sets that are symbolized by those circles.
Outside the circles: In a Venn diagram, an element that is positioned outside every circle does not belong to any of the sets being represented.
D. This is so because these components are a part of the intersection of the two sets and as such, they are a part of both sets. In set theory, all of the components that are shared by two sets are contained in their intersection. Due to their simultaneous membership in both sets, the elements at the intersection are a subset of both sets.
To learn more about Venn diagram link is here
brainly.com/question/33510078
#SPJ3
Mr Williams earns $32,350 per year. If his state income tax is 3%, how much state income tax does Mr Williams owe per year?
Answers
Answer:
Step-by-step explanation:
32350*3%= $970.50
help me pleasee, my brain won't work

Answers
The given fractions have equal value, so Liam is correct.
How to find the equivalent fractions?Equivalent fractions are defined as fractions that have different numerators and denominators but the same value. For example, 2/4 and 3/6 are equivalent fractions because they are both equal to 1/2. A fraction is part of a whole. Equivalent fractions represent the same part of a whole.
Liam is claiming that the fraction -(5/12) is equivalent to 5/-12.
Thus, we can say that:
The fraction -(5/12) can be described as the opposite of a positive number divided by a positive number. A positive number divided by a positive number always results in a positive quotient and its' opposite is always negative.
The fraction 5/-12 can be described as a positive number divided by a negative number which always results in a negative quotient
The fractions have equal value, so Liam is correct
Read more about Equivalent fractions at: https://brainly.com/question/17220365
#SPJ1
Ifm22 = 115°, what is m21?
Answers
Answer:
Step-by-step explanation:
95ft 40ft 65 ft what is the area of this trapezoid
Answers
You can find the area of the trapezoid using the following formula:
\(\begin{gathered} A=\frac{a+b}{2}\times h \\ \text{Where:} \\ a=Long\text{ base=95ft} \\ b=\text{short base=65ft} \\ h=\text{height}=40ft \\ A=\frac{95+65}{2}\times40=80\times40=3200ft^2 \end{gathered}\)Find the value of a in the equation below.
5 = x - 18
Answers
Answer:
There's no A so I'm going to assume you meant X
X = 23
Step-by-step explanation:
X is equal to 23, because 23 - 18 = 5
or 5 + 18 = 23
A small computing center has found that the number of jobs submitted per day to its computers has a distribution that is approximately bell shaped, with a mean of 64 jobs and a standard deviation of 12. Where do we expect most (approximately 95%) of the distribution to fall
Answers
We expect approximately 95% of the distribution to fall within two standard deviations of the mean.
In a bell-shaped distribution, known as a normal distribution, approximately 95% of the values are expected to fall within two standard deviations of the mean. Given that the mean number of jobs submitted per day is 64 and the standard deviation is 12, we can calculate the range within which 95% of the distribution is expected to fall.
To find the range, we multiply the standard deviation by 2 and then add and subtract this value from the mean:
Lower range: 64 - (2 * 12) = 40
Upper range: 64 + (2 * 12) = 88
Therefore, we expect that approximately 95% of the distribution of the number of jobs submitted per day will fall within the range of 40 to 88.
Based on the given mean of 64 jobs and a standard deviation of 12, we can expect that approximately 95% of the distribution will fall within the range of 40 to 88 jobs submitted per day. This indicates the central portion of the distribution where the majority of the data points are likely to be located in a bell-shaped distribution.
To know more about standard deviations visit:
https://brainly.com/question/475676
#SPJ11
is 3 * 10(to power -x) an exponential function?
Answers
Answer:
Step-by-step explanation:
The function f(x)=3x is an exponential function; the variable is the exponent. If f(x) = ax, then we call a the base of the exponential function. The base must always be positive.
The boss told the management team some sad news too. “I’m cutting your hourly pay. You now get paid per project you finish. I will give you $10 for each finished schedule you create and $20 for each meeting you complete! You cannot make more than $100 per day! Also you must make more than twice as many schedules as meetings!”
Create a system of linear inequalities to model the situation above, where x is the number of schedules made and y is the number of meetings completed.
Answers
The system of linear inequalities to model the situation is 10x + 20y ≤ 100 and y > 2x
How to create a system of linear inequalities to model the situationFrom the question, we have the following parameters that can be used in our computation:
Each finished schedule = $10Each meeting = $20Amount to make = Not more than $100You must make more than twice as many schedules as meetingsUsing the following representations:
x = the number of schedules madey = the number of meetings completedWe have the following system of inequalities from the given statements
10x + 20y ≤ 100
y > 2x
Hence, the system of inequalities is 10x + 20y ≤ 100 and y > 2x
Read more about system of inequalities at
https://brainly.com/question/4180576
#SPJ1
What is 5 x 100 + 3 + 10 + 8 x 0.1 + 9 x 0.009
Answers
Answer:
513.881
Explanation: (Credits to jessy276)
= 5*100+3+10+8*0.1+9*0.009
= 500+3+10+8*0.1+9*0.009
= 500+3+10+0.8+9*0.009
= 500+3+10+0.8+0.081
= 503+10+0.8+0.081
= 513+0.8+0.081
= 513.8+0.081
= 513.881
Answer:
The answer is 513.881
Step-by-step explanation
PLEASE help what would it be?
Answers
Answer: #8292829282
Step-by-step explanation:
A square calendar has sides that are 9 inches long. What is the area?
Answers
Answer:
81 because area=lxh so 9x9 is 81
\(i \: hope \: it \: will \: hellp \: you \: \)
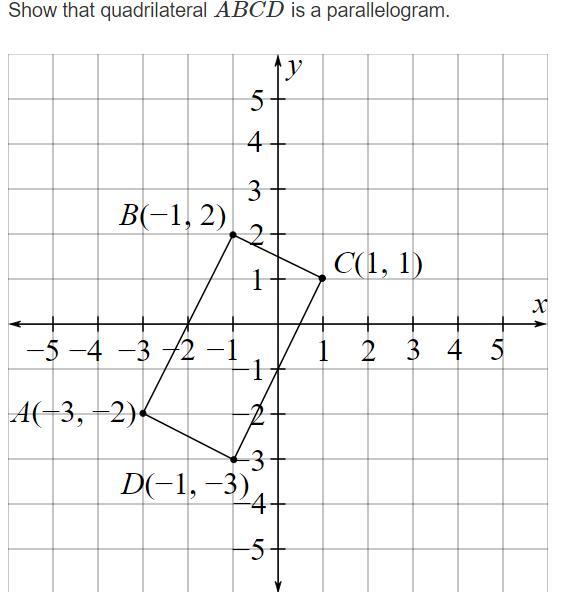
Show that quadrilateral ABCD is a parallelogram.

Answers
Slope of AB = 2; Slope of DC = 2
Slope of AD = -1/2; Slope of BC = -1/2
Both pairs of opposite sides are parallel because they have the same slope, therefore, quadrilateral ABCD is a parallelogram.
What is a Parallelogram?A parallelogram is a quadrilateral that has two pairs of opposite sides that have the same lengths and are parallel to each other.
Since the opposite sides of a parallelogram are parallel, therefore, they have the same slope value.
Slope = change in y / change in x.
Find the slope of AB and DC. then AD and BC:
Slope of AB = (-2 - 2)/(-3 -(-1)) = -4/-2
Slope of AB = 2
Slope of DC = (-3 - 1)/(-1 - 1) = -4/-2
Slope of DC = 2
Slope of AD = (-3 -(-2))/(-1 -(-3)) = -1/2
Slope of AD = -1/2
Slope of BC = (2 - 1)/(-1 - 1) = 1/-2
Slope of BC = -1/2
Therefore, since AB and DC have the same slope, they are parallel, so also is AD and BC parallel because they have the same slope, therefore, quadrilateral ABCD is a parallelogram.
Learn more about parallelogram on:
https://brainly.com/question/3050890
#SPJ1
Jane bought 5 apples at $120 each. She sells them to John to make a profit of 10%. What is the selling price of each apple?
Answers
Answer:
she resells each apple for $132
Step-by-step explanation:
I multiplied 120 by 0.1 to find how much she would be marking up the price of each apple. I got the answer of $12. So then I added that $12 to $120 and got the new price of $132.
I checked my work I swear it's correct
hope this helps chu <3
The following cone has a slant height of 17
cm and a radius of 8
cm.
What is the volume of the cone?
Responses
480π
320π
544π
Answers
The formula for the volume of a cone is:
V = (1/3)πr²h
where r is the radius of the base, h is the height of the cone, and π is pi.
In this case, the slant height is given as 17 cm, which we can use with the radius to find the height of the cone using the Pythagorean theorem:
h² = s² - r²
h² = 17² - 8²
h² = 225
h = 15
Now that we have the height, we can plug in the values for r and h into the formula for the volume:
V = (1/3)π(8²)(15)
V = (1/3)π(64)(15)
V = (1/3)(960π)
V = 320π
Therefore, the volume of the cone is 320π cubic cm. Answer: 320π.
how is the size of a sample related to the spread of the sampling distribution
Answers
The spread of the sampling distribution is equal to the standard deviation divided by the square root of the sample size.
What is sample size?
The sample size is defined as the number of observations used to estimate a given population. The population was used to determine the size of the sample. The process of selecting a subset of individuals from a population to estimate the characteristics of the entire population is known as sampling. For analysis, the number of entities in a subset of a population is chosen.
The spread of the sampling distribution is proportional to the spread of the sample and its size. We calculate the spread of the sampling distribution as the population standard deviation divided by the square root of the sample size.
To learn more about the size of a sample, click on the below link:
https://brainly.com/question/14172957
#SPJ4
Find the Product of (s^2+5s)(s^3+4s^2).
Answers
The result of the product \((s^2+5s)(s^3+4s^2)\) is \(s^5+9s^4+20s^3\)
The product is given as:
\((s^2+5s)(s^3+4s^2)\)
Rewrite as:
\((s^2+5s)(s^3+4s^2) = (s^2+5s) \times (s^3+4s^2)\)
Expand the expression on the right-hand side
\((s^2+5s)(s^3+4s^2) = s^2\times (s^3+4s^2)+5s \times (s^3+4s^2)\)
Distribute the expressions
\((s^2+5s)(s^3+4s^2) = s^5+4s^4+5s^4+20s^3\)
Evaluate like terms
\((s^2+5s)(s^3+4s^2) = s^5+9s^4+20s^3\)
Hence, the result of the product \((s^2+5s)(s^3+4s^2)\) is \(s^5+9s^4+20s^3\)
Read more about products at:
https://brainly.com/question/24963015
the president of a university claimed that the entering class this year appeared to be larger than the entering class from previous years but their mean sat score is lower than previous years. he took a sample of 30 of this year's entering students and found that their mean sat score is 1,501 with a standard deviation of 53. the university's record indicates that the mean sat score for entering students from previous years is $1,520. he wants to find out if his claim is supported by the evidence at a 5% significance level. which of the following best describes a type i error? the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed not lower the president concludes that the mean sat score of the entering students is higher than previous years when it is indeed higher the president concludes that the mean sat score of the entering students is not lower than previous years when it is indeed lower the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed lower
Answers
The result is not statistically significant.
To test the hypothesis is the mean SAT score is less than 1520 at 5% significance level.
The null hypothesis is
H₀ : μ ≥ 1520
The alternative hypothesis is
Hₐ : μ ≤ 1520
then the test statistic is,
t = (x - μ)/(s/√n)
= (1501 - 1520)/(53/√20)
t = - 1.603
The t-test statistic is - 1.603.
Degree of freedom n - 1 = 20 - 1 = 19
Hence the t-critical value is -1.792.
The conclusion is that the t value corresponds to sample statistics is not fall in the critical region, so the null hypothesis is not rejected at 5% level of significance. There is insignificance evidence indicates that the mean SAT score is less than 1520.
The result is not statistically significant.
To know more about mean score here
https://brainly.com/question/16907497
#SPJ4
What evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
⚠️⚠️ Least to greatest please ⚠️⚠️ it’s my 5/6th question and I need help

Answers
Answer:
2, 4, 1, 3
Step-by-step explanation:
maybe