Highschool students were surveyed about which math and science topics they preferred , they were asked to choose algebra or geometry, and biology or chemistry. The results are shown in the frequency table below.
Use this table to create a relative frequency table by row.

Answers
Here is the completed table:
Algebra Geometry Total
Biology 73% 27% 100%
Chemistry 70% 30% 100%
Total 72% 28% 100%
What are the relative frequencies?
Relative frequency measures how often a value appears relative to the sum of the total values. It is the ratio of a particular value to the total sum of values.
Algebra Geometry Total
Biology 67/92 25/92 92/92
Chemistry 46/66 20/66 66/66
Total 113/158 45/158 158/158
Algebra Geometry Total
Biology 0.728 0.272 1
Chemistry 0.697 0.303 1
Total 0.715 0.284 1
Algebra Geometry Total
Biology 73% 27% 100%
Chemistry 70% 30% 100%
Total 72% 28% 100%
To learn more about relative frequency, please check: https://brainly.com/question/26577861
#SPJ1
Related Questions
Determine the area under the standard normal curve that lies to the right of the z-score of 1.44. (Use a four-digit decimal. No rounding necessary.)
Answers
Answer:
The area is 0.0749
Step-by-step explanation:
The area under the standard normal curve represents probability and has a total value of 1
Now, to the right of the z-score 1.44, the area we are considering is the probability below;
P( z > 1.44)
To get this value, we need to use the standard normal distribution table
Checking this, the probability is
P( z > 1.44) = ) = 0.074934 which is 0.0749 for a four decimal digit
Solve the inequality 46 > y + 11
Answers
Answer:
Inequality Form:
y<35
Interval Notation:
(−∞,35)
Answer:
y is smaller than 34 or less
Step-by-step explanation:
put the 11 to the other side and make it a negative then you get 46-11=35 than it says 35>y
What Pythagorean triple is made using the Pythagorean identity and the following numbers?
x = 2, y = 1
1. 3, 4, 5
2. 4, 1, 25
3. 2, 1, 2
4. 4, 1, root 5.
Answers
The Pythagorean triples here are; 3, 4, 5. Option 1
What is a Pythagorean triple?We define a Pythagorean triple as a^2+b^2 = c^2 where a, b and c are the three positive integers. Given that we can find the Pythagorean triple from; (x2 - y2)2 + (2xy)2 = (x2 + y2)2
Where; x = 2, y = 1
Substituting values have;
(2^2 - 1^2)^2 + (2*2*1)^2 = (2^2 + 1^2)^2
This results to;
3^2 + 4^2 = 5^2
9 + 16 = 25
25=25
Therefore the Pythagorean triples here are; 3, 4, 5. Option 1
Learn more about Pythagorean triples:https://brainly.com/question/15190643
#SPJ1
b) Select a patient from the waiting room: the patient has diabetes or the patient
takes insulin.
Determine if they are mutually exclusive
Answers
Answer:
Not mutually exclusive because you can have a patient that does both
what is the formula of total surface area of cuboid.
Answers
This diagram shows a pre-image △ABC and its image, △A′′B′′C′′ , after a series of transformations.
Select from the drop-down menus to correctly complete the statements.
△ABC is
1. reflected across the y-axis.
2. rotated 90 degrees counterclockwise about the origin.
3. translated 4 units right
to become △A′B′C′. Then △A′B′C′ is
1. reflected across the x-axis.
2. reflected across the line y = x
3. rotated 90 degrees counterclockwise about the origin
to become △A′′B′′C′′ . Because the transformations are
1. both rigid
2.not both rigid,
The pre-image and image are
1. congruent
2. not congruent

Answers
Using translation concepts, we have that:
△ABC is 3. translated 4 units right to become △A′B′C′. Then, △A′B′C′ is 3. rotated 90 degrees counterclockwise about the origin to become △A′′B′′C′′ .Because the transformations are both rigid, the pre-image and the image are congruent.What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction either in it’s definition or in it’s domain. Examples are shift left/right or bottom/up, vertical or horizontal stretching or compression, and reflections over the x-axis or the y-axis.
On the translation of △ABC to △A′B′C′, the rule applied to the vertices is:
(x,y) -> (x + 4, y).
Hence it was translated 4 units right.
On the translation of △A′B′C′ to △A′′B′′C′', the rule is given by:
(x,y) -> (-y,x).
Hence it was rotated 90 degrees counterclockwise about the origin.
The triangle keeps the same size after the translations, hence:
Because the transformations are both rigid, the pre-image and the image are congruent.
More can be learned about translations at https://brainly.com/question/4521517
#SPJ1
Help me please I need help x^2 - 8x + 16

Answers
The set of factors used to factor the given trinomial are -4 and -4. Therefore, option C is the correct answer.
The given trinomial is x²-8x+16.
Factors of 16 Sum of factors
-1 and -16 -1+(-16)=-17
-2 and -8 -2+(-8)=-10
-4 and -4 -4+(-4)=-8
The set of factors would used to factor the trinomial are -4 and -4.
Therefore, option C is the correct answer.
To learn more about the factorisation of polynomial visit:
https://brainly.com/question/16789195.
#SPJ1
1 y + 4/5 = 1 2/5
what is y?
Answers
Answer: y = 3/5
Step-by-step explanation:
To solve for y, isolate the variable on one side and constants on the other side:
1y = 1 2/5 - 4/5
(You can subtract 4/5 on both sides to get rid of it on the left side and subtract it from 1 2/5 on the right side)
Now, you can solve for y.
y = 7/5 - 4/5 = 3/5
help me find the slope please
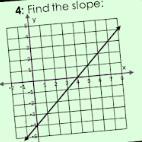
Answers
Answer:
3/4
Step-by-step explanation:
Ok, so I see that the x-intercept is (4,0), while the y-intercept is(-3,0)
Slope is rise/run
Between these two points, the line rose 3 and horizontally went 4 units to the right. Therefore, the slope is 3/4.
Feel free to tell me if I did anything wrong! :)
Also, if you're still confused, I could explain it another way.
Please solve with explanation (high points)

Answers
a) From the Pythagorean theorem, we have
AC² = AB² + BC² = a² + a² ⇒ AC = √2 a
and
AK² = AB² + BK² = a² + (2a)² ⇒ AK = √5 a
ABCD and BKLC are perpendicular, so AC and CL are perpendicular and ∆ACL is a right triangle. By the Pythagorean theorem, we have
AL² = AC² + CL² = (√2 a)² + (2a)² ⇒ AL = √6 a
Now,
AK² + LK² = (√5 a)² + a² = 6a² = (√6 a)² = AL²
which means ∆AKL satisfies the Pythagorean theorem and is a right triangle, so ∠AKL = 90°.
b) We know AC = √2 a and AK = √5 a. By the Pythagorean theorem, we find
CK² = BC² + BK² = a² + (2a)² ⇒ CK = √5 a
By the law of cosines, we have
AK² = AC² + CK² - 2 AC CK cos(∠AKC)
6a² = 2a² + 5a² - 2√10 a² cos(∠AKC)
cos(∠AKC) = 1/(2√10)
∠AKC = arccos(1/(2√10)) ≈ 80.9°
Find the exact length of the curve. x = et − t, y = 4et/2, 0 ≤ t ≤ 6
Answers
Length of the curve is e² - 1 .
In arithmetic, a function from a group X to a group Y assigns to every part of X precisely one part of Y. The set X is termed the domain of the function and therefore the set Y is termed the codomain of the function
Main body:
A parametric curve is a function expressed in components form, such that;
x = f(t) , y = g(t).
The length of a parametric curve on the interval a ≤ t ≤ b is given by the definite integral :
L = \(\int\limits^a_b {\sqrt{\frac{dx}{dt}^2 + {\frac{dy}{dt}^2 } } } \, dx\)
Let's begin by getting the first derivative of the components of the function with respect to the variable t.
x = e^t - t
dx / dt = e^t−1
And, y = 4 e^t/2
dy /dt = 2 e^t/2
Substitute the derivatives into the following definite integral which computes the length of the parametric curve on the interval
[a,b]=[0,2].
L = \(\int\limits^a_b {\sqrt{\frac{dx}{dt}^2 + {\frac{dy}{dt}^2 } } } \, dx\)
L= \(\int\limits^2_0 {\sqrt{\ (e^t - 1)^2 + ({\(2e^{t/2}) ^2 } } } \, dx\)
L = \(\int\limits^2_0 {e^t - 1} \, dx\)
Evaluate the solution at the limits of integration to get the length.
L = (e² - 1 )- (e⁰ - 1)
L = e² - 1 - 1 + 1
L= e² - 1
Hence , length of the curve is e² - 1 .
To know more about length of the curve , visit:
brainly.com/question/29364263
#SPJ1
Identify the measure of MN in the diagram.
Answers
find area in square yards of trapezoid 5 yards, 23 yards base and 12 yards height
Answers
Answer:
I found the area its 168, I converted it to square yards 0.12963.
Step-by-step explanation:
Answer:
Step-by-step explanation:
Formula
Area = (b1 + b2) * h /2
Givens
b1 = 5 yards
b2 = 23 yards
h = 12 yards
Solution
Area = (5 + 23)*12 / 2
Area = (28)*12/2 Divide by 2
Area = 28*6 Combine
Area = 168 Yards^2
Please help
Me
I need to finish this I will give brainlest

Answers
Only the opposite edges of a rectangle's parallel and congruent angles are congruent. Although the sides and angles of a trapezoid may not always be identical, at least one set of its sides must be parallel.
what is parallel lines?In geometry, parallel lines are coplanar unlimited lines that never cross. In a particular three-dimensional space, the parallel planes represent the ones that never cross. Parallel curves are those with a constant minimum separation between them and no places of contact or intersection. In geometry, parallel lines are two lines which run in the exact same plane, evenly spaced apart, and hadn't cross. Both vertical and horizontal can be used. In commonplace items like train tracks, stacks of notebooks, and crossings for pedestrians, straight lines can be seen.
The form of Jackson's poster is best described as a rhombus. A quadrilateral with a rhombus has opposing sides that are parallel and all of its sides are equal. Additionally, it has congruent opposing angles. In addition to having parallel opposing sides, a parallelogram also has non-congruent sides and angles. Only the opposite edges of a rectangle's parallel and congruent angles are congruent. Although the sides and angles of a trapezoid may not always be identical, at least one set of its sides must be parallel.
To know more about parallel lines visit:
https://brainly.com/question/16701300
#SPJ1
Write the equation in standard form

Answers
Answer:
standard form: Ax + By = C
Slope-intercept form: y=mx+b
where m is the slope and b is the y intercept.
first lets put this into intercept form:
y=-5x+b
(4, 0) is the x intercept.)
To find what b is plug in the point 4, 0 for the x and y of the equation:
0=-5(4)+b
0=-20+b
20=b
b=20
Now that we have the slope, m, and the y intercept, b, we can make our equation
y=-5x+20
Now we need to transform this equation into standard form like so:
y=-5x+20
5x+y=20 - this is your answer
Step-by-step explanation:
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
(12sin(pi/2x)*lnx)/((x³+5)(x-1))
lim as x approaches 1
Answers
The limit of the given function as x approaches 1 is 0.
To find the limit of the given function as x approaches 1, we need to evaluate the expression by substituting x = 1. Let's break it down step by step:
1. Begin by substituting x = 1 into the numerator:
\(\[12\sin\left(\frac{\pi}{2}\cdot 1\right)\ln(1) = 12\sin\left(\frac{\pi}{2}\right)\ln(1) = 12(1)\cdot 0 = 0\]\)
2. Now, substitute x = 1 into the denominator:
(1³ + 5)(1 - 1) = 6(0) = 0
3. Finally, divide the numerator by the denominator:
0/0
The result is an indeterminate form of 0/0, which means further analysis is required to determine the limit. To evaluate this limit, we can apply L'Hôpital's rule, which states that if we have an indeterminate form 0/0, we can take the derivative of the numerator and denominator and then evaluate the limit again. Applying L'Hôpital's rule:
4. Take the derivative of the numerator:
\(\[\frac{d}{dx}\left(12\sin\left(\frac{\pi}{2}x\right)\ln(x)\right) = 12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{x} + \frac{\sin\left(\frac{\pi}{2}x\right)\ln(x)}{x}\right)\]\)
5. Take the derivative of the denominator:
\(\[\frac{d}{dx}\left((x^3 + 5)(x - 1)\right) = \frac{d}{dx}\left(x^4 - x^3 + 5x - 5\right) = 4x^3 - 3x^2 + 5\]\)
6. Substitute x = 1 into the derivatives:
Numerator: \(\[12\left(\cos\left(\frac{\pi}{2}\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{1} + \sin\left(\frac{\pi}{2}\right) \cdot \frac{\ln(1)}{1}\right) = 0\]\)
Denominator: 4(1)³ - 3(1)² + 5 = 4 - 3 + 5 = 6
7. Now, reevaluate the limit using the derivatives:
lim as x approaches 1 of \(\[\frac{{12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{{-1}}{{x}} + \sin\left(\frac{\pi}{2}x\right) \cdot \frac{{\ln(x)}}{{x}}\right)}}{{4x^3 - 3x^2 + 5}}\]\)
= 0 / 6
= 0
Therefore, the limit of the given function as x approaches 1 is 0.
For more such questions on L'Hôpital's rule
https://brainly.com/question/24116045
#SPJ8
Out of a group of 3 people, 2 study French and 1 studies Spanish. Two people are drawn randomly from the group without replacement. Display all possible outcomes as an organized list.
Answers
Answer:
- 1 French, 1 Spanish
- 2 French
What is the value of X on the parallelogram below?

Answers
Because (2(44)+16)=104 is a true statement
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9 } A= {1, 2, 3, 4} and B= {4, 5, 6, 7}. Draw the Venn diagram of A ∩B. Answer with full explanation and diagram will be marked as brainliest for sure!!!
Answers
Step-by-step explanation:
Its mean the same number for both A and B which is only 4.

3. A certain sum of money at simple interest amounts to $560 in 3 years and to
$600 in 5 years. Find the principal and the rate of interest. [Ans. $ 500; 4%]
Answers
Answer: principal value = $500 and rate of interest = 4%.
Step-by-step explanation:
Let P = Principal value, r= rate of interest, t= time.
Formula for simple interest:
Interest = P x r x t
Final amount = P+ interest
= P+Prt
= P(1+rt)
Simple interest amounts to $560 in 3 years.
⇒ 560= P(1+3r)
\(\Rightarrow\ P=\dfrac{560}{1+3r}\) (i)
Simple interest amounts to $600 in 5 years.
⇒ 600= P(1+5r)
\(\Rightarrow\ P=\dfrac{600}{1+5r}\) (ii)
From (i) and (ii) , we get
\(\dfrac{560}{1+3r}=\dfrac{600}{1+5r}\\\\\Rightarrow\ 560(1+5r)=600(1+3)\\\\\Rightarrow\ 560+2800r=600+1800r\\\\\Rightarrow\ 2800r-1800r=600-560\\\\\Rightarrow\ 1000r=40\\\\\Rightarrow\ r=\dfrac{40}{1000}\\\\\Rightarrow\ r= 0.04= 4\%\)
Put r= 0.04 in (ii), we get
\(P=\dfrac{600}{1+5(0.04)}\\\\=\dfrac{600}{1+0.2}\\\\=\dfrac{600}{1.2}\\\\=500\)
Hence, principal value = $500 and rate of interest = 4%.
.An artist sells his paintings at a gallery. He charges a set price for each small painting K and
each large painting he sells. Last month, the artist sold 6 small paintings and 8 large
paintings and earned $670 in all. This month, he sold 12 small paintings and 10 large
paintings and earned $950 in all. How much does the artist charge for a small painting?
How much does he charge for a large painting?
I need this in system of equation form please.
Answers
The artist charges $25 for a small painting and $65 for a large painting.
How to substitute two equations?
To substitute one equation into another, you can replace one of the variables in the second equation with the expression from the first equation.
Let K be the price of small painting and L be the price of large painting.
From the information given, we know that:
Last month:
6K + 8L = $670 (1)
This month:
12K + 10L = $950 (2)
We have two equations and two unknowns, so we can use a system of equations to find the values of K and L.
Solving the system of equations:
From (1) equation, we have:
6K + 8L = $670
From (2) equation, we have:
12K + 10L = $950
Now we can solve for K (small painting) by multiplying equation (1) by 2 and equation (2) by -1 and adding the two equations together:
12K + 16L = $1340
-12K - 10L = -$950
0K + 6L = $390
Therefore, L = $390 / 6 = $65
Now we can substitute this value of L back into the first equation (1) and solve for K:
6K + 8($65) = $670
6K = $670 - 8($65) = $670 - $520 = $150
K = $150 / 6 = $25
So, the artist charges $25 for a small painting and $65 for a large painting.
To learn more about Substitute two equation,visit
https://brainly.com/question/25869125
#SPJ1
Please help pleaseee

Answers
Answer:
It's A
Step-by-step explanation:
\(\frac{12}{\sqrt{3} }=4\sqrt{3}\)
\(4\sqrt{3}*2=8\sqrt{3}\)
help due in 5 min!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!will mark brainliest if correct!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Answers
Answer:
what do u need help with
Step-by-step explanation:
??
Consider A Triangle ABC. Suppose That A= 119 Degrees, B=53, And C=57. Solve The Traingle
Answers
9514 1404 393
Answer:
a = 94.8, B = 29.3°, C = 31.7°
Step-by-step explanation:
Side 'a' can be found using the Law of Cosines:
a² = b² +c² -2bc·cos(A)
a = √(2809 +3249 -6042·cos(119°)) ≈ √8987.22 ≈ 94.8
Then one of the other angles can be found from the Law of Sines.
sin(C)/c = sin(A)/a
C = arcsin(c/a·sin(A)) ≈ arcsin(0.525874) ≈ 31.7°
Then the remaining angle can be found to be ...
B = 180° -A -C = 180° -119° -31.7° = 29.3°
__
The solution is a ≈ 94.8, B ≈ 29.3°, C ≈ 31.7°.

Pls help its due at 11:10

Answers
Answer:
firstly
we all know that the angles of a triangle they all add up to 180° meaning when you add them all they must give you 180°
88°+33°+L = 180° ( sum of angle in a ∆)
121° + L = 180°
L = 180° - 121°
L = 59°
Step-by-step explanation:
first you you must add all your angles and all equal to 180°
that you add the like terms
than you transpose 121° to the right hand side
What’s a negative number that has an absolute value greater than 8?
Answers
Answer:
any negative number less than -8
x<-8
Step-by-step explanation:
|x|>8
we know x<0
so
-x>8
x<-8
Shamin Jewelers sells diamond necklaces for $442 less 10%. Jewelers offers the same necklace for $527 less 34%, 14% What additional rate of discount must offer to meet the competitor's price
Answers
Answer:
The selling price of the diamond necklace at Shamin Jewelers after 10% discount is:
$442 * 0.9 = $397.80
The selling price of the same necklace at the competitor's store after 34% and 14% discount is:
$527 * 0.66 * 0.86 = $247.08
So, Shamin Jewelers needs to offer an additional discount to meet the competitor's price:
$397.80 - $247.08 = $150.72
To calculate the additional rate of discount, we divide the difference by the original selling price at Shamin Jewelers and multiply by 100:
($150.72 / $442) * 100 = 34.11%
Therefore, Shamin Jewelers must offer an additional 34.11% discount to meet the competitor's price.
Step-by-step explanation:
which one of the following is a solution to |2x-1|>3 A.2, B.-1, C.-2, D.1, E.None of these
Answers
Therefore x>2 or x<-2
—> E
whats 1/5 x 26 estimated
Answers
Answer:
About five
Step-by-step explanation:
The answer is 5.2, rounded up is 5.
Hope this helps!