Answers
The normal distribution has the following behavior:
First question

Related Questions
help with 1 b please. using ln.

Answers
Answer:
\(\displaystyle \frac{dy}{dx} = \frac{1}{(x - 2)^2\sqrt{\frac{x}{2 - x}}}\)
General Formulas and Concepts:
Pre-Algebra
Equality PropertiesAlgebra I
Terms/CoefficientsFactoringExponential Rule [Root Rewrite]: \(\displaystyle \sqrt[n]{x} = x^{\frac{1}{n}}\)Algebra II
Natural logarithms ln and Euler's number eLogarithmic Property [Exponential]: \(\displaystyle log(a^b) = b \cdot log(a)\)Calculus
Differentiation
DerivativesDerivative NotationImplicit DifferentiationDerivative Property [Multiplied Constant]: \(\displaystyle \frac{d}{dx} [cf(x)] = c \cdot f'(x)\)
Derivative Property [Addition/Subtraction]: \(\displaystyle \frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[g(x)]\)
Basic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Derivative Rule [Quotient Rule]: \(\displaystyle \frac{d}{dx} [\frac{f(x)}{g(x)} ]=\frac{g(x)f'(x)-g'(x)f(x)}{g^2(x)}\)
Derivative Rule [Chain Rule]: \(\displaystyle \frac{d}{dx}[f(g(x))] =f'(g(x)) \cdot g'(x)\)
Step-by-step explanation:
*Note:
You can simply just use the Quotient and Chain Rule to find the derivative instead of using ln.
Step 1: Define
Identify
\(\displaystyle y = \sqrt{\frac{x}{2 - x}}\)
Step 2: Rewrite
[Function] Exponential Rule [Root Rewrite]: \(\displaystyle y = \bigg( \frac{x}{2 - x} \bigg)^\bigg{\frac{1}{2}}\)[Equality Property] ln both sides: \(\displaystyle lny = ln \bigg[ \bigg( \frac{x}{2 - x} \bigg)^\bigg{\frac{1}{2}} \bigg]\)Logarithmic Property [Exponential]: \(\displaystyle lny = \frac{1}{2}ln \bigg( \frac{x}{2 - x} \bigg)\)Step 3: Differentiate
Implicit Differentiation: \(\displaystyle \frac{dy}{dx}[lny] = \frac{dy}{dx} \bigg[ \frac{1}{2}ln \bigg( \frac{x}{2 - x} \bigg) \bigg]\)Logarithmic Differentiation [Derivative Rule - Chain Rule]: \(\displaystyle \frac{1}{y} \ \frac{dy}{dx} = \frac{1}{2} \bigg( \frac{1}{\frac{x}{2 - x}} \bigg) \frac{dy}{dx} \bigg[ \frac{x}{2 - x} \bigg]\)Chain Rule [Basic Power Rule]: \(\displaystyle \frac{1}{y} \ \frac{dy}{dx} = \frac{1}{2} \bigg( \frac{1}{\frac{x}{2 - x}} \bigg) \bigg[ \frac{2}{(x - 2)^2} \bigg]\)Simplify: \(\displaystyle \frac{1}{y} \ \frac{dy}{dx} = \frac{-1}{x(x - 2)}\)Isolate \(\displaystyle \frac{dy}{dx}\): \(\displaystyle \frac{dy}{dx} = \frac{-y}{x(x - 2)}\)Substitute in y [Derivative]: \(\displaystyle \frac{dy}{dx} = \frac{-\sqrt{\frac{x}{2 - x}}}{x(x - 2)}\)Rationalize: \(\displaystyle \frac{dy}{dx} = \frac{-\frac{x}{2 - x}}{x(x - 2)\sqrt{\frac{x}{2 - x}}}\)Rewrite: \(\displaystyle \frac{dy}{dx} = \frac{-x}{x(x - 2)(2 - x)\sqrt{\frac{x}{2 - x}}}\)Factor: \(\displaystyle \frac{dy}{dx} = \frac{-x}{-x(x - 2)^2\sqrt{\frac{x}{2 - x}}}\)Simplify: \(\displaystyle \frac{dy}{dx} = \frac{1}{(x - 2)^2\sqrt{\frac{x}{2 - x}}}\)Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation
Book: College Calculus 10e
In a recent Super Bowl, a TV network predicted that 25 % of the audience would express an interest in seeing one of its forthcoming television shows. The network ran commercials for these shows during the Super Bowl. The day after the Super Bowl, and Advertising Group sampled 150 people who saw the commercials and found that 30 of them said they would watch one of the television shows. Suppose you have the following null and alternative hypotheses for a test you are running:
H0:p=0.53H0:p=0.53
Ha:p≠0.53Ha:p≠0.53Calculate the test statistic.
Answers
Answer:
The right solution is "-8.25".
Step-by-step explanation:
The given values are:
Sampled people,
n = 150
Null and alternative hypotheses will be:
\(H_0:p=0.53\)
\(Ha:p\neq 0.53\)
The z-statistics will be:
⇒ \(z=\frac{\bar{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n} } }\)
On substituting the values, we get
⇒ \(=\frac{0.2-0.53}{\sqrt{\frac{0.53(1-0.53)}{150} } }\)
⇒ \(=\frac{-0.33}{\sqrt{\frac{0.24}{150}} }\)
⇒ \(=\frac{-0.33}{0.04}\)
⇒ \(=-8.25\)
What the the Quotient 7/12 divided by 2/5
Answers
Answer:35/24
Step-by-step explanation:
7/12 ➗ 2/5
Next step we change divide sign to multiplication,with the numerator and denominator of the right hand fraction inverted
7/12 x 5/2
(7x5)/(12x2)
35/24
The quotient of 7/12 divided by 2/5 is 35/24.
To divide fractions, you need to multiply the first fraction by the reciprocal (or the multiplicative inverse) of the second fraction.
The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
So, to find the quotient of 7/12 divided by 2/5, you multiply 7/12 by the reciprocal of 2/5, which is 5/2.
Here are the steps:
Write down the first fraction: 7/12
Write down the reciprocal of the second fraction: 5/2
Multiply the first fraction by the reciprocal: (7/12) x (5/2)
Multiply the numerators: 7 x 5 = 35
Multiply the denominators: 12 x 2 = 24
Simplify the fraction, if possible: 35/24
Therefore, the quotient of 7/12 divided by 2/5 is 35/24.
Learn more about fraction click;
https://brainly.com/question/10354322
#SPJ6
The Weibull distribution is widely used in statistical problems relating to aging of solid insulating materials subjected to aging and stress. Use this distribution as a model for time (in hours) to failure of solid insulating specimens subjected to AC voltage. The values of the parameters depend on the voltage and temperature; suppose ? = 2.7 and ? = 220.(a) What is the probability that a specimen's lifetime is at most 250? Less than 250? More than 300? (Round your answers to four decimal places.)
at most 250, less than 250, more than 300.
(b) What is the probability that a specimen's lifetime is between 100 and 250? (Round your answer to four decimal places.)
(c) What value is such that exactly 50% of all specimens have lifetimes exceeding that value? (Round your answer to three decimal places.)hr
Answers
Answer:
Step-by-step explanation:
Given that
\(\alpha =2.5\) ,\(\beta =220\)
The weibull distribution with parameters \(\alpha \ \ and \ \ \beta\)
where \(\alpha =0 \ \ , \beta =0\)
\(F(x,\alpha ,\beta) \left|\begin{array}{cc}\frac{\alpha }{\beta } x^{\alpha-1e^-(x/\beta)^\alpha &x\geq 0\\0&x<0\end{array}\right\)
Then,
\(F(x,\alpha ,\beta )=\left|\begin{array}{cc}0&x<0\\1-e^-^{(x/\beta)}^\alpha &x\geq 0\end{array}\right\)
A) The probability that a specimen's lifetime is at most 250 is
\(P(X\leq 250)=F(250,2.7,220)\\\\=1-e^-^(250/220)^{2.7}\\\\=1-0.2436\\\\=0.7564\)
The probability that the specimen's life time is more than 300 is
\(P(X>300)=1-P(X\leq 300)\\\\=1-F(300;2.7,220)\\\\=1-(1-e^-^{(300/220)^{2.7}\)
\(=e^-^{(300/220)^{2.7}\)
= 0.0992
b)The probability of the specimen's lifetime is between 100 and 250
\(P(100<X<250)=P(X<250)-P(X<100)\\\\=F(250;2.7,220)-F(100;2.7,220)\\\\=(1-e^-^{(250/220)^2^.^7})-(1-e^-^{(100/220)^2^.^7})\\\\=(1-0.2436)-1(1-0.8878)\\\\=0.6442\)
c) The value such that exactly 50% of all specimens have lifetimes exceeding that value is
\(P(X>x)=0.50\\\\1-P(X<x)=0.50\\\\1-(1-e^-^{(x/220)^{2.7}}=0.50\\\\e^-^{(x/220)^{2.7}}=0.50\\\\-(x/220)^{2.7}=In(0.50)\\\\(x/220)^{2.7}=-In(0.50)\\\\(x/220)=[-In(0.50)]^{(\frac{1}{2.7})} \\\\x=220[-In(0.50)]^{(\frac{1}{2.7})}\)
x = 192.07
The demand for bicycles is modeled by the function f(x) = - x ^ 2 + 5x + 14 where x represents the number of stores in a city that sell bicycles. A company wants to know when the demand is positive
the interval (- 2, 7) a reasonable solution to when the demand is positive?
Yes. The interval (- 2, 7) is a reasonable solution because the function is positive in that region
No The interval (- 2, 7) is not a reasonable solution because the lett endpoint is negative and there cannot be a negative number of stores.
The interval (- 2, 7) is not a reasonable solution because the function is negative in that region;
Yes The interval (- 2, 7) a reasonable solution because the endpoints of the interval are roots of the function

Answers
Answer:d
Step-by-step explanation:i
What is the solution to the system of equations below?
314
-
12 and y=-4x-31
O (-4,-15)
O (-4,-12)
O (4,-9)
O (4,-47)
Answers
The solution of the given equations is (-4,-15). Hence option A is the correct option.
What is an equation?
If two expressions are connected with an equal sign and at least one expression contains a variable then it is an equation.
Given equations are
y=3/4x-12 ....(i)
y=-4x-31 ....(ii)
Equate equations (i) and (ii)
3/4x-12 = -4x-31
Add 12 on both sides:
3/4x = -4x-31 + 12
Add 4x on both sides:
3/4x + 4x = -31 + 12
19/4x = -19
x = -4
Putting x=-4 in equation (ii)
y=-4(-4)-31
y = 16 - 31
y = -15
To learn more about the system of equations click on the below link:
https://brainly.com/question/29026989
#SPJ1
the sum of negative three and a number, divided by seven, is negative two
Answers
Answer:
-3+x/7=-2 is equation, 7 is the answer
Step-by-step explanation:
-3+x/7=-2 add 3 to both sides.
x/7=1 multiply 7 to both sides
x=7 this is the answer
I will mark brainlist please help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee eeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Step-by-step explanation:
similar by AA
that is the answer
The point A (p, -2) is mirrored in the point B (6,-q). The image is A'(4, -8). What is p and q?
Answers
Answer:
p =4
q = -2
Step-by-step explanation:
To mirror is to reflect. See the picture

Todd rolled a 12-sided die marked with the numbers 1 to 12. These are his experimental probabilities.
P(odd number) = 18/48
P(greater than 8) = 16/48
P(9) = 12/48
1. Which experimental probability matches the theoretical probability exactly?
2. Which experimental probability is farthest from the theoretical probability?
Answers
The experimental probability farthest from the theoretical probability is P(greater than 8). The theoretical probability of rolling a 9 is 1/12 because there is one 9 out of twelve total possible outcomes.
Experimental probability refers to the probability of an event based on data acquired from repeated trials or experiments.
Theoretical probability is the probability of an event occurring based on logical reasoning or prior knowledge. In Todd’s case, he rolled a 12-sided die marked with the numbers 1 to 12.
The probabilities are as follows:P(odd number) = 18/48P(greater than 8) = 16/48P(9) = 12/48To answer the questions:1. Which experimental probability matches the theoretical probability exactly?The theoretical probability of rolling an odd number is 6/12 or 1/2 because there are six odd numbers out of the twelve total possible outcomes.
The experimental probability Todd obtained was 18/48. Simplifying 18/48 to lowest terms gives 3/8, which is equal to 1/2, the theoretical probability.
Therefore, the experimental probability that matches the theoretical probability exactly is P(odd number).2. Which experimental probability is farthest from the theoretical probability? The theoretical probability of rolling a number greater than 8 is 3/12 or 1/4 because there are three numbers greater than 8 out of twelve total possible outcomes.
The experimental probability Todd obtained was 16/48. Simplifying 16/48 to lowest terms gives 1/3, which is not equal to 1/4, the theoretical probability.
The experimental probability Todd obtained was 12/48. Simplifying 12/48 to lowest terms gives 1/4, which is not equal to 1/12, the theoretical probability.
However, the difference between the experimental probability and the theoretical probability for P(9) is smaller than that of P(greater than 8). Therefore, P(greater than 8) is the experimental probability that is farthest from the theoretical probability.
For more such questions on possible outcomes
https://brainly.com/question/30241901
#SPJ8
You can answer any of the two or both the problem is find the value of x

Answers
Answer: (4x+24)=4⋅(x+6) =28
11x+33= 11⋅(x+3) =44
6x-6= 6⋅(x−1)=0
Step-by-step explanation:
I NEED THIS ANSWER FAST PLEASE
Fill in the missing coordinates of the x-intercept of the line defined by the equation y = x – 4

Answers
Answer:
the answer might be (-4,0) for x coordinates
Help please!
S = 180m
How many strides would a runner take during a 1-hour run (60 min)
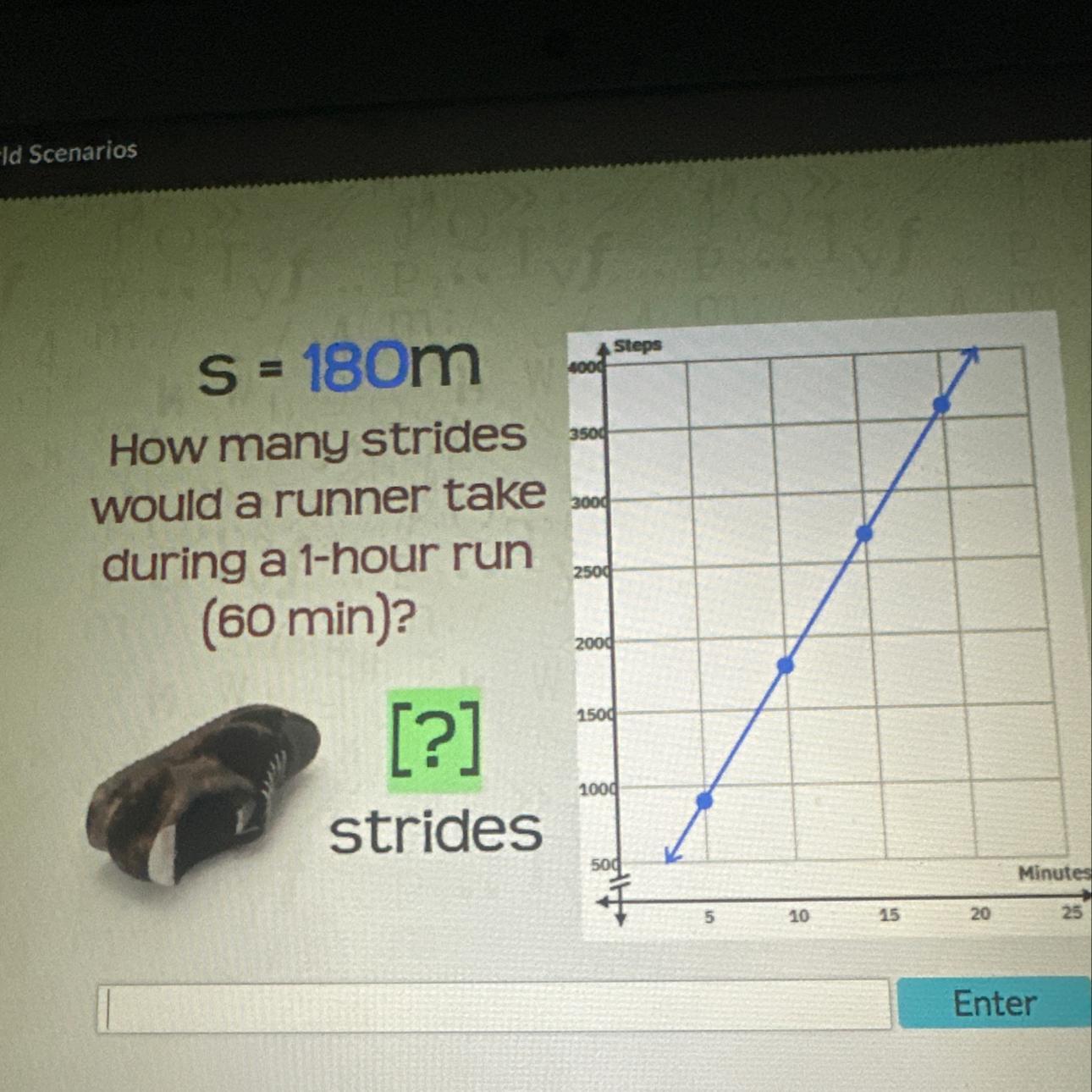
Answers
The number of strides the runner will make during 1 hour run will be =
10,800.
How to calculate the total number of strides made by the runner in a hour?To calculate the distance or number of strides made by the runner in an
hour, the graph given above is considered as follows;
The y-axis which represents the number of strides is plotted against the x-axis which is the number of hours.
From the graph
20 minutes= 3600 strides
60 minutes = X strides
make X the subject of formula;
x= 3600×60/20
= 216000/20
= 10,800
Learn more about distance here:
https://brainly.com/question/30694816
#SPJ1
What are all the terms in the expression 4mn + m + 5 and which is a constant
Answers
Answer:
m and n are variables whereas 4 and 5 are constant terms or coefficient.
Step-by-step explanation:
hope it will help ^_^
Answer:
Below
Step-by-step explanation:
● 4 and 5 are constants since their values don't change.
● m and n are variables since they can take any value.
A business owner wants to know if it will be profitable to open a new coffee shop in a nearby town.In towns where the shop has been successful,the shop name is recognizable to people 53% of the time .He survey random sample of 12 residents of the town
Answers
Complete question :
A business owner wants to know if it will be profitable to open a new coffee shop in a nearby town.In towns where the shop has been successful,the shop name is recognizable to people 53% of the time .He survey random sample of 12 residents of the town. Find the probability that among these 12 surveyed residents, none of them have ever heard of the coffee shop
Answer:
0.000116
Step-by-step explanation:
Using the binomial probability relation :
Probability of success, p = 0.53
1 - p = 0.47
Number surveyed, n = 12
P(x =x) = nCx * p^x * (1 - p)^(n - x)
Probability that none has heard of the coffee shop :
P(x = 0) = 12C0 * 0.53^0 * 0.47^12
P(x = 0) = 0.000116
16-18 help please !!!!!!

Answers
Answer:
not sure but -2
Step-by-step explanation: I did on calculator
16-18= -2
since 18 is a larger number than 16 the answer would go into a negative
At a local pizza shop 2 pizzas will serve 6 people.
How many people will 8 pizzas serve?
Answers
1pizza serves 6/2 people
8pizza serves 6/2*8
=24people
8pizza serves 24 people
Please look at the photo for the question. Thank you!

Answers
The function g(x) = x² + 4x has a: A. minimum.
The minimum value occur at x = -2.
The function's minimum value is -4.
How to determine the axis of symmetry and vertex of a quadratic function?In Mathematics, the axis of symmetry of a quadratic function can be calculated by using this mathematical equation:
Axis of symmetry = -b/2a
Where:
a and b represents the coefficients of the first and second term in the quadratic function.
For the given quadratic function g(x) = x² + 4x, we have:
a = 1, b = 4, and c = 0
Axis of symmetry, Xmax = -b/2a
Axis of symmetry, Xmax = -(4)/2(1)
Axis of symmetry, Xmax = -2
Next, we would determine vertex as follows;
g(x) = x² + 4x
g(-2) = -(-2)² + 4(-2)
g(-2) = -4.
Read more on quadratic functions here: brainly.com/question/14201243
#SPJ1
the time needed to complete a final examination in a particular college course is normally distributed with a mean of 77 minutes and a standard deviation of 12 minutes. answer the following questions.
Answers
The probability of a student completing the final examination in less than 65 minutes is 13.45%.
The time it takes to complete a final examination in a particular college course is normally distributed with a mean of 77 minutes and a standard deviation of 12 minutes. This can be expressed mathematically as X~N(77, 12).
The probability of a student completing the final examination in less than 65 minutes can be calculated by using the Z-score formula:
Z = (x - μ) / σ
Where x = 65 minutes, μ = 77 minutes, and σ = 12 minutes.
Plugging these values into the formula, we get:
Z = (65 - 77) / 12 = -1.17
Using a Z-score table, we can find the probability of a student completing the final examination in less than 65 minutes, which is equal to 0.1345, or 13.45%. Therefore, the probability of a student completing the final examination in less than 65 minutes is 13.45%.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
Complete question :What is the probability of a student taking 90 minutes or less to finish the exam?
At $450 per person, an airline anticipates selling 300 tickets for a particular flight. At $500 p person, the airline anticipates selling 150 tickets for the same flight. Assume a linear relation between the cost per ticket C and the number of tickets, x sold. Whi the following equations can be used to model the given information?C=-(2)/(3)x+555C=-(2)/(3)x+550C=-(1)/(3)x+555C=-(1)/(3)x+550

Answers
1) We can begin by writing C as a function of x and find the slope between two points (300,450) and (150,500)
\(\begin{gathered} C=mx+b \\ m=\frac{y_2-y_1}{x_2-x_1}=\frac{500-450}{150-300}=\frac{50}{-150}=-\frac{1}{3} \end{gathered}\)2) Now that we know the slope, we need to find the linear coefficient (y-intercept), using one of those ordered pairs: (150,500)
\(\begin{gathered} 500=-\frac{1}{3}(150)+b \\ -\frac{1}{3}\left(150\right)+b=500 \\ -50+b=500 \\ b=550 \end{gathered}\)So the function is:
\(C=-\frac{1}{3}x+550\)
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
What are the dimensions, a, b, and c, of the net? a = cm b = cm c = cm
Answers
Which expression is equivalent to 200k¹5, if k + 0?
O A. 2k¹225
O B. 2k5 25
O c.
O D.
8k5/25
8kv/25

Answers
Answer: Choice B
\(2k^5\sqrt[3]{25}\)
================================================
Work Shown:
\(\sqrt[3]{200k^{15}}\\\\\sqrt[3]{8*25k^{5*3}}\\\\\sqrt[3]{8*25(k^5)^3}\\\\\sqrt[3]{8(k^5)^3*25}\\\\\sqrt[3]{8(k^5)^3}*\sqrt[3]{25}\\\\2k^5\sqrt[3]{25}\)
------------------------
Explanation:
The goal is to factor the radicand in such a way that we pull out perfect cube factors.
Notice that 200 = 8*25 and 8 is a perfect cube (since 2^3 = 8). It is the largest perfect cube factor of 200.
We can rewrite the k^15 as k^(5*3) which is equivalent to (k^5)^3
Once these perfect cube factors are pulled out, they cancel with the cube root to get what you see above.
Please help me solve

Answers
The value of -7A - 4B would be
\(-7A-4B=\left[\begin{array}{ccc}-15&59&-3\\16&61&-83\\-45&-99&-106\end{array}\right]\)
Option (A) is correct.
What is a matrix?
A matrix is a rectangular array or table of numbers, symbols, or expressions that are arranged in rows and columns to represent a mathematical object or a property of such an object in mathematics. For instance, consider a matrix with two rows and three columns.
The given matrices are
\(A=\left[\begin{array}{ccc}-3&-9&-3\\-4&-3&9\\7&9&-10\end{array}\right]\)\(B=\left[\begin{array}{ccc}9&1&6\\3&-10&5\\-1&9&-9\end{array}\right]\)
Now we have to find the value of '-7A - 4B'.
\(-7A-4B=-7\left[\begin{array}{ccc}-3&-9&-3\\-4&-3&9\\7&9&-10\end{array}\right]-4\left[\begin{array}{ccc}9&1&6\\3&-10&5\\-1&9&-9\end{array}\right]\\\\\\-7A-4B = \left[\begin{array}{ccc}21&63&21\\28&21&-63\\-49&-63&70\end{array}\right]-\left[\begin{array}{ccc}36&4&24\\12&-40&20\\-4&36&106\end{array}\right]\\\\\\-7A-4B=\left[\begin{array}{ccc}-15&59&-3\\16&61&-83\\-45&-99&-34\end{array}\right]\)
Hence, the value of -7A - 4B would be
\(-7A-4B=\left[\begin{array}{ccc}-15&59&-3\\16&61&-83\\-45&-99&-106\end{array}\right]\).
To learn more about operations on matrices, visit:
https://brainly.com/question/18291235
#SPJ1
In most acceptance sampling plans, when a lot is rejected, the entire lot is inspected and all defective items are replaced. When using this technique the AOQ: worsens (AOQ becomes a larger fraction). improves (AOQ becomes a smaller fraction). is not affected, but the AQL is improved. is not affected. falls to zero.
Answers
Answer:
When using this technique, the AOQ:
improves (AOQ becomes a smaller fraction).
Step-by-step explanation:
AOQ simply means Average Outgoing Quality, which improves with inspection. It is a part of an organization's Acceptance Sampling Plan, usually designed to meet product quality and risk level targets. The plan draws samples from a population of items. Then it tests the samples. It only accepts the entire population if the sample is considered good enough. It also rejects the population when the sample is poor enough. In the plan, information about sample size and critical acceptance or rejection numbers are clearly indicated. Acceptance sampling is common in most business environments because it has been found to be more economical than doing 100% inspection of incoming production input and output.
Which expression is always equivalent to sin x when 0° < x < 90°?
(1) cos (90°- x)
(3) cos (2x)
(2) cos (45° - x)
(4) cos x
Answers
The expression that is always equivalent to sin x when 0° < x < 90° is (1) cos (90° - x). Option 1
To understand why, let's analyze the trigonometric functions involved. In a right triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Since we are considering angles between 0° and 90°, we can guarantee that the side opposite the angle will always be the shortest side of the triangle, and the hypotenuse will be the longest side.
Now let's examine the expression cos (90° - x). The cosine of an angle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. In a right triangle, when we subtract an angle x from 90°, we are left with the complementary angle to x. This means that the remaining angle in the triangle is 90° - x.
Since the side adjacent to the angle 90° - x is the same as the side opposite the angle x, and the hypotenuse is the same, the ratio of the adjacent side to the hypotenuse remains the same. Therefore, cos (90° - x) is equivalent to sin x for angles between 0° and 90°.
On the other hand, options (2) cos (45° - x) and (3) cos (2x) do not always yield the same value as sin x for all angles between 0° and 90°. The expression cos x (option 4) is equivalent to sin (90° - x), not sin x.
Option 1 is correct.
For moresuch questions on equivalent visit:
https://brainly.com/question/2972832
#SPJ8
Calc II Question
Sketch the region enclosed by the given curves and find its area.
Y = lxl , y = x^2 - 2
Answers
Answer:
\(\displaystyle A=\frac{20}{3}\)
Step-by-step explanation:
\(\displaystyle A=\int^2_{-2}(|x|-(x^2-2))\,dx\\\\A=2\int^2_0(x-(x^2-2))\,dx\\\\A=2\int^2_0(-x^2+x+2)\,dx\\\\A=2\biggr(-\frac{x^3}{3}+\frac{x^2}{2}+2x\biggr)\biggr|^2_0\\\\A=2\biggr(-\frac{2^3}{3}+\frac{2^2}{2}+2(2)\biggr)\\\\A=2\biggr(-\frac{8}{3}+2+4\biggr)\\\\A=2\biggr(-\frac{8}{3}+6\biggr)\\\\A=2\biggr(\frac{10}{3}\biggr)\\\\A=\frac{20}{3}\)
Bounds depend on whether you use -x or +x instead of |x|, but you double regardless. See the attached graph for a visual.

9. The following histogram is for the weights (lbs) of 63 male
college students.
a) What is the best description for the approximate shape
of this distribution?
A. Symmetric.
C. Skewed to the right. D. Bimodal
B. Skewed to the left.
b) In the histogram, how many males' weights show to be less than 150 lbs?
c) What proportion (percentage) of the weights of males is more than 230 lbs?

Answers
The distribution is bimodal (a), eight men weigh less than 150 lbs (b), and the percentage of males that weigh more than 230 lbs is 3.17%.
What can be observed in this histogram?A: Distribution: The distribution can be classified as bimodal, which means there are two peaks in the graph.
B. The number of males that weigh less than 150 lbs can be determined as follows:
110 - 120 lbs = 2 males
130 -140 lbs = 2 males
140 - 150 lbs = 4 males
2 + 2 + 4 = 8 males
C. The percentage of males that weigh more than 230 lbs can be calculated as follows:
63 = 100%
2 = x
x= 2 x 100 / 63
x = 200 / 63 = 3.17%
Learn more about histograms in https://brainly.com/question/16819077
#SPJ1
"What is the rest wavelength of an emission line observed at 2148 nanometers in a galaxy 100
Megaparsecs away from the Milky Way? Your answer should be significant to four digits."
Answers
The rest wavelength of the emission line observed at 2148 nanometers in the galaxy 100 million light-years away is approximately 2103 nanometers.
The rest wavelength of an emission line can be determined by applying the concept of redshift, which is a phenomenon observed in astrophysics where light from distant objects is shifted towards longer wavelengths due to the expansion of the universe.
In this case, the emission line is observed at 2148 nanometers (or 2.148 micrometers) in a galaxy located 100 million light-years away. To calculate the rest wavelength, we need to consider the redshift factor. Redshift, denoted by z, is defined as the observed wavelength divided by the rest wavelength minus 1.
Given that the observed wavelength is 2.148 micrometers and the galaxy is located 100 million light-years away, we need to convert the distance into a redshift factor using the cosmological relationship between redshift and distance. Assuming a standard cosmological model, we can use the Hubble constant to estimate the redshift.
The Hubble constant represents the rate at which the universe is expanding. Taking a typical value of the Hubble constant as 70 kilometers per second per megaparsec, we find that the redshift factor, z, is approximately 0.021.
To determine the rest wavelength, we rearrange the redshift equation as \((observed wavelength) = (1 + z) \times (rest wavelength)\). Substituting the values, we get \((2.148 micrometers) = (1 + 0.021) \times (rest wavelength).\)
Simplifying the equation, we find the rest wavelength to be approximately 2.103 micrometers or 2103 nanometers.
For more such questions on rest wavelength
https://brainly.com/question/31327842
#SPJ8
Find the perimeter and the area of each shape. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answers
Answer:
Circumference: 12π + 8 cm,
Area: 48 ( cm )^2
Step-by-step explanation:
This figure is composed of circles, squares, and semicircles. As you can see, the squares indicate that each semicircle should have ( 1 ) the same area, and ( 2 ) the same length ( circumference ). It would be easier to take the circumference of the figure first, as it is composed of arcs part of semicircles the same length.
Circumference of 1 semicircle = \(\frac{1}{2}\)( πd ) = \(\frac{1}{2}\)π( 4 ) = 2π ( cm )
Circumference of Figure (composed of 6 semicircles + 2 sides of a square),
We know that 6 semicircles should be 6 \(*\) 2π, and as the sides of a square are equal - if one side is 4 cm, the other 3 are 4 cm as well. Therefore the " 2 sides of a square " should be 2
Circumference of Figure = 6 \(*\) 2π + 2 = 12π + 8 ( cm )
_____________
The area of this figure is our next target. As you can see, it is composed of 3 semicircles, and the area of 3 semicircles subtracted from the area of 3 squares. Therefore, let us calculate the area of 1 semicircle, and the area of 1 square first.
Area of 1 semicircle = 1/2π\(r^2\) = 1/2π\((2)^2\) = 2π ( cm ),
Area of 1 square = ( 4 cm )( 4 cm ) = 16 ( \(cm^2\) )
So, the area of the figure should be the following -
Area of Figure = 3 \(*\) 2π + 3( 16 - 2π ) = 48 ( cm )^2
