Answers
Answer:
\(\displaystyle f'(1) = 6\)
General Formulas and Concepts:
Calculus
Differentiation
DerivativesDerivative NotationDerivative Property [Multiplied Constant]: \(\displaystyle \frac{d}{dx} [cf(x)] = c \cdot f'(x)\)
Derivative Property [Addition/Subtraction]: \(\displaystyle \frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[g(x)]\)
Basic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Step-by-step explanation:
Step 1: Define
Identify
\(\displaystyle f(x) = 5x - 1 + \ln x\)
Step 2: Differentiate
[Function] Derivative Property [Addition/Subtraction]: \(\displaystyle f'(x) = \frac{d}{dx}[5x] - \frac{d}{dx}[1] + \frac{d}{dx}[\ln x]\)Rewrite [Derivative Property - Multiplied Constant]: \(\displaystyle f'(x) = 5 \frac{d}{dx}[x] - \frac{d}{dx}[1] + \frac{d}{dx}[\ln x]\)Derivative Rule [Basic Power Rule]: \(\displaystyle f'(x) = 5 - 0 + \frac{d}{dx}[\ln x]\)Logarithmic Differentiation: \(\displaystyle f'(x) = 5 + \frac{1}{x}\)Substitute in x: \(\displaystyle f'(1) = 5 + \frac{1}{1}\)Simplify: \(\displaystyle f'(1) = 6\)Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation
Related Questions
88 is a solution to 1/8x=11 because
Answers
See below...
(1/8)x = 11
Muliply 8 on both sides...
x = 88
What is the equation of the line that passes through the point (5, -6) and has a
slope of -3/5?
Answers

Lucy want divide 18.6by 1.2 in order to estimate the quotient which is the best expression to use
Answers
Answer:
░░░░░░░░░░░░░░░░░░░░░▄▀░░▌
░░░░░░░░░░░░░░░░░░░▄▀▐░░░▌
░░░░░░░░░░░░░░░░▄▀▀▒▐▒░░░▌
░░░░░▄▀▀▄░░░▄▄▀▀▒▒▒▒▌▒▒░░▌
░░░░▐▒░░░▀▄▀▒▒▒▒▒▒▒▒▒▒▒▒▒█
░░░░▌▒░░░░▒▀▄▒▒▒▒▒▒▒▒▒▒▒▒▒▀▄
░░░░▐▒░░░░░▒▒▒▒▒▒▒▒▒▌▒▐▒▒▒▒▒▀▄
░░░░▌▀▄░░▒▒▒▒▒▒▒▒▐▒▒▒▌▒▌▒▄▄▒▒▐
░░░▌▌▒▒▀▒▒▒▒▒▒▒▒▒▒▐▒▒▒▒▒█▄█▌▒▒▌
░▄▀▒▐▒▒▒▒▒▒▒▒▒▒▒▄▀█▌▒▒▒▒▒▀▀▒▒▐░░░▄
▀▒▒▒▒▌▒▒▒▒▒▒▒▄▒▐███▌▄▒▒▒▒▒▒▒▄▀▀▀▀
▒▒▒▒▒▐▒▒▒▒▒▄▀▒▒▒▀▀▀▒▒▒▒▄█▀░░▒▌▀▀▄▄
▒▒▒▒▒▒█▒▄▄▀▒▒▒▒▒▒▒▒▒▒▒░░▐▒▀▄▀▄░░░░▀
▒▒▒▒▒▒▒█▒▒▒▒▒▒▒▒▒▄▒▒▒▒▄▀▒▒▒▌░░▀▄
▒▒▒▒▒▒▒▒▀▄▒▒▒▒▒▒▒▒▀▀▀▀▒▒▒▄▀
Step-by-step expla i think its c
The correct answer is option C, 20 divided by 1,
We have to given that,
Lucy want divide 18.6 by 1.2 in order to estimate the quotient.
Now, Divide the numbers as,
⇒ 18.6 ÷ 1.2
⇒ 18.6 / 1.2
⇒ 186/12
⇒ 83/6
⇒ 15.5
Here, The best expression to use to estimate the quotient,
⇒ 18.6 ÷ 1.2
Since, 18.6 ≈ 20
and, 1.2 ≈ 1
Hence, For the quotient of 18.6 divided by 1.2, the best expression to use is 20 divided by 1.
This is because 20 is close to 18.6, and 1 is close to 1.2.
Using this expression, we can estimate the quotient as 20 divided by 1, which is simply 20.
This estimate is close to the actual quotient, which is 15.5, and is easier to calculate mentally.
Therefore, the correct answer is option C, 20 divided by 1, which is the best expression to use in order to estimate the quotient of 18.6 divided by 1.2.
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ2
Complete question is,
Lucy wants to divide 18.6 by 1.2. In order to estimate the quotient, which is the best expression to use?
10 divided by 1
10 divided by 2
20 divided by 1
20 divided by 2
I think the pic is attached to this

Answers
The y-intercept of a line in the xy-plane is (0,1) as shown in attached graph given int the question.
To find the y-intercept of a line in the xy-plane, we need to find the point where the line intersects the y-axis. The y-axis is the vertical axis that runs through the origin and is perpendicular to the x-axis. This means that the y-intercept is the value of y when x is equal to zero. Therefore, we can read off the y-intercept directly from the equation of the line. To find the y-intercept of a line in the xy-plane, we need to find the point where the line intersects the y-axis. The y-axis is the vertical axis that runs through the origin and is perpendicular to the x-axis.
In the given graph we can see that the line intersects the point 1 on y axis.
Therefore, y-intercept of a line in the xy-plane is (0,1).
Learn more about xy-plane :
https://brainly.com/question/29276653
#SPJ1
How is this A? Or is it wrong? This is polynomials

Answers
Answer:
D
Step-by-step explanation:
The volume for a rectangular prism is given by the formula:
\(V=lwh\)
The length is 2h, the width is 9-h, and the height is h. So:
\(V=2h(h)(9-h)\)
Multiply the first two terms:
\(V=2h^2(9-h)\)
Distribute:
\(V=18h^2-2h^3\)
Our answer is D.
I hope this helps!
what factors in the global and local environment are conducive to the development of ai?
Answers
Artificial Intelligence (AI) is a branch of computer science focused on the creation of intelligent machines that work and react like humans. AI, unlike traditional programming, uses algorithms to enable machines to learn from their experiences, identify patterns in the data, and make decisions.
Factors in the global and local environment conducive to the development of AI are discussed below:
Global Environment: The following factors in the global environment are conducive to AI development: Advancement in Technology: In recent years, there has been a rapid advancement in technology. Various factors such as Big Data, the Internet of Things (IoT), and the Cloud have contributed to the development of AI. With the rise of automation in businesses and industries, AI has become more important than ever before. Investment: Companies such as Microsoft, and Amazon are investing heavily in AI. Tech start-ups are also mushrooming all over the world, focusing on AI, making it a competitive industry with a promising future. Demographic Change: Changes in the global demographic profile may lead to an increase in demand for AI. AI applications, such as autonomous cars, are being developed to meet the needs of an aging population, while virtual assistants are being developed to support younger generations.
Local Environment: Local factors also play an important role in the development of AI. These include The Availability of Talent: The availability of a skilled workforce is crucial for the development of AI. Companies need to hire data scientists, AI developers, and engineers, who can build and maintain AI models. Infrastructure: AI systems require high-end infrastructure such as servers, storage, and bandwidth. The availability of this infrastructure is important for AI development. Education: Education is an essential factor in the development of AI. With the rise of AI, educational institutions must incorporate AI in their curriculum to ensure that graduates have the necessary skills to meet the demands of the industry. Funding: The availability of funding is crucial for AI development. Governments and private institutions should invest in AI start-ups, research, and development, to ensure that AI reaches its full potential.
To learn more about global and local environments conducive to the development visit:
https://brainly.in/question/8438186
#SPJ11
I need help ASAP!!!
g(x) = x2 - 2x2 + x
g(3) =
Answers
Answer:
-6
Step-by-step explanation:
put the value of x=3 in the equation g(x)
someone help me please with this algebra problem
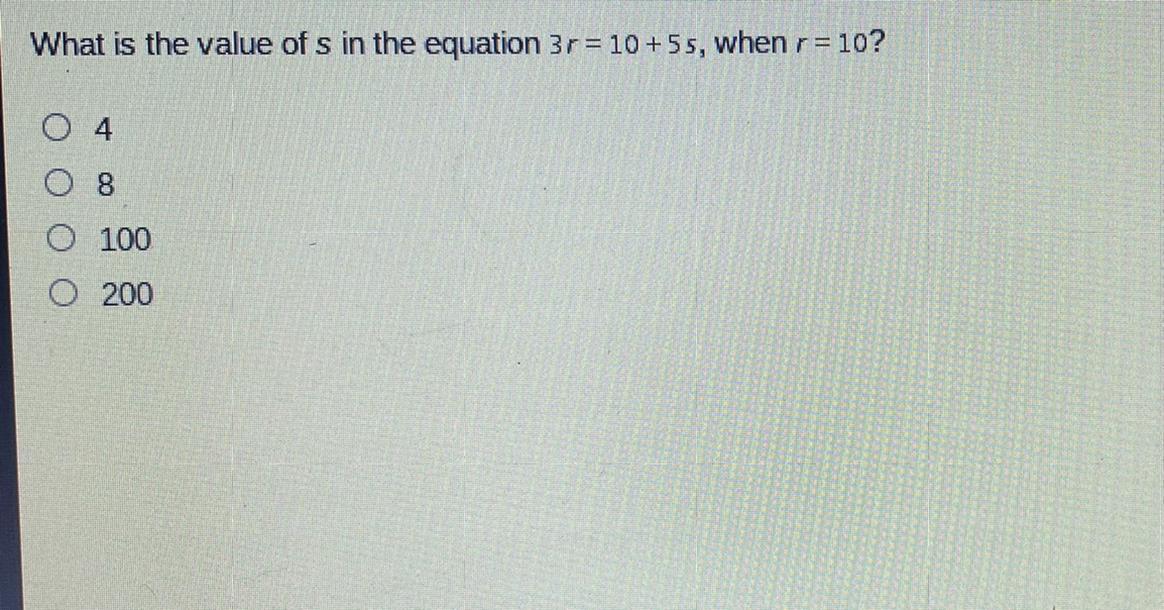
Answers
Answer:
4
Step-by-step explanation:
3r = 10 + 5s
r = 10
3(10) = 10 + 5s
30 = 10 + 5r
20 = 5r
r = 4
whats 5 x 2x x 2y?? im doing hw and im confused
Answers
Because
5 x 2x = 10x
10x x 2y = 20xy
Distribute: 2x ( 3 + 8x) *
Answers
Answer:16x^2+6x
Step-by-step explanation:
find the first partial derivatives and evaluate each at the given point. function point w = 3x2y − 7xyz 10yz2 (4, 3, −2)
Answers
The partial derivatives of the given function at the point (4, 3, -2) is equal to wₓ(4, 3, -2) = 114 , \(w_{y}\)(4, 3, -2) = -16 , and\(w_{z}\)(4, 3, -2) = 96.
Function w= 3x²y − 7xyz + 10yz²
and Point (4, 3, −2)
To find the partial derivatives of the function w = 3x²y - 7xyz + 10yz² with respect to x, y, and z,
Differentiate each term of the function separately and evaluate them at the given point (4, 3, -2).
Partial derivative with respect to x (wₓ).
To find wₓ,
differentiate each term with respect to x while treating y and z as constants.
wₓ = d(3x²y)/dx - d(7xyz)/dx + d(10yz²)/dx
Differentiating each term,
wₓ = 6xy - 7(yz) - 0 since there is no x term in the last term.
Now, substitute the given point (4, 3, -2) into the expression for wₓ.
wₓ(4, 3, -2)
= 6(4)(3) - 7(3)(-2)
= 72 + 42
= 114
Partial derivative with respect to y (\(w_{y}\)).
To find \(w_{y}\),
differentiate each term with respect to y while treating x and z as constants.
\(w_{y}\)= d(3x²y)/dy - d(7xyz)/dy + d(10yz²)/dy
Differentiating each term.
\(w_{y}\) = 3x² - 7xz + 20yz
Substitute the given point (4, 3, -2) into the expression for \(w_{y}\)
\(w_{y}\)(4, 3, -2)
= 3(4)² - 7(4)(-2) + 20(3)(-2)
= 48 + 56 - 120
= -16
Partial derivative with respect to z ( \(w_{z}\))
To find \(w_{z}\), we differentiate each term with respect to z while treating x and y as constants:
\(w_{z}\) = d(3x²y)/dz - d(7xyz)/dz + d(10yz²)/dz
Differentiating each term.
since there is no z term in the first term
\(w_{z}\) = 0 - 7xy + 20y²
Substitute the given point (4, 3, -2) into the expression for \(w_{z}\)
\(w_{z}\)(4, 3, -2)
= -7(4)(3) + 20(3)²
= -84 + 180
= 96
Therefore, the partial derivatives of the function w = 3x²y - 7xyz + 10yz² at the point (4, 3, -2) are,
wₓ(4, 3, -2) = 114
\(w_{y}\)(4, 3, -2) = -16
\(w_{z}\)(4, 3, -2) = 96
learn more about partial derivative here
brainly.com/question/17514349
#SPJ4
The above question is incomplete , the complete question is:
Find the first partial derivatives with respect to x, y, and z, and evaluate each at the given point.
Function w= 3x²y − 7xyz + 10yz² and Point (4, 3, −2)
wₓ(4, 3, −2) =
wy(4, 3, −2) =
wz(4, 3, −2) =
Describe the slope of the line.
(In image)

Answers
Answer:
The slope is negative, and m = -3/5
Step-by-step explanation:
The line is going down, so the slope is negative, and using the slope formula, m = -3/5.
12. Look for Relationships In the graph of a
vertical motion model shown, how is the initial
velocity related to the vertex of the parabola?

Answers
The vertical component of the initial velocity will basically decide where the vertices will be. that is how the initial velocity is related to the vertex of the parabola.
Describe Parabola?A parabola is a symmetrical curve that is formed by the intersection of a plane and a cone, where the plane is parallel to one of the cone's generating lines. The shape of a parabola is similar to that of a U-shaped curve, but with a sharper curve near the bottom of the U.
The parabola has several important properties, including a focus and a directrix. The focus is a point on the axis of symmetry of the parabola that is equidistant from every point on the curve. The directrix is a line that is perpendicular to the axis of symmetry and is equidistant from every point on the curve.
The equation of a parabola in standard form is y = ax² + bx + c, where "a" determines the direction and shape of the parabola, "b" determines the horizontal shift of the parabola, and "c" determines the vertical shift of the parabola.
The initial velocity will have two component basically, a horizontal component and a vertical component. The vertical component will decide how high the object will go, or in other words the vertical component of the velocity will decide the position of the vertex of the parabolis path which the object is going to follow.
When the vertical component of the velocity becomes 0, the object will be at it's maximum height (i.e the object will be at the vertex of the parabola)
The vertical component of the initial velocity will basically decide where the verties will be. that is how the initial velocity is related to the vertex of the parabola.
To know more about velocity visit:
https://brainly.com/question/11950136
#SPJ1
PLEASE HELP IDK WHAT TO DO

Answers
You have the correct pairings
(x,y) is any point on the line
m is the slope
(x1,y1) is the given point on the line
------------------------------
For example, if we said that the slope was m = 5 and the given point was (x1,y1) = (7,9)
Then,
y - y1 = m(x - x1)
y - 9 = 5(x - 7)
is the point slope form
The student’s t distribution will approach the standard normal distribution as the number of the degrees of freedom goes up.
a. True
b. False
Answers
Answer:
True student distribution will approach the standard
12 pens cost $6.55 What is the unit cost of each pen? Round.
$0.58
$0.52
$0.54
$0.55
Answers
Answer:
$0.55
Step-by-step explanation:
6.55/12=0.54583333333
5+ is a rounded up
bellow 5 round down
.545 is all we need to know to round to .55
What is the approximate volume of a cone with a radius of 1. 75 feet and a height of 2. 1 feet?.
Answers
The approximate volume of the cone with a radius of 1.75 feet and a height of 2.1 feet is approximately 6.478875 cubic feet.
To calculate the approximate volume of a cone, you can use the formula:
Volume = (1/3) * π * r^2 * h,
where r represents the radius of the cone's base and h represents the height of the cone.
Given that the radius (r) is 1.75 feet and the height (h) is 2.1 feet, we can substitute these values into the formula:
Volume = (1/3) * π * (1.75)^2 * 2.1
To calculate the approximate volume, we'll use the value of π as approximately 3.14:
Volume ≈ (1/3) * 3.14 * (1.75)^2 * 2.1
Now, we can perform the calculations:
Volume ≈ (1/3) * 3.14 * 3.0625 * 2.1
≈ 1.047 * 3.0625 * 2.1
≈ 6.478875
Therefore, the approximate volume of the cone with a radius of 1.75 feet and a height of 2.1 feet is approximately 6.478875 cubic feet.
Learn more about volume here
https://brainly.com/question/463363
#SPJ11
You have $5 and your opponent has $10. You flip a fair coin and if heads comes up, your opponent pays you $1. If tails comes up, you pay your opponent $1. The game is finished when one player has all the money or after 100 tosses, whichever comes first. Use simulation to estimate the probability that you end up with all the money and the probability that neither of you goes broke in 100 tosses.
Answers
The probability of neither player going broke is much higher, at about 15.25%.
What is probability?Probability is a way to gauge how likely something is to happen. Many things are difficult to predict with absolute certainty.
This game can be modeled as a random walk, where the number of heads minus the number of tails represents the player's net winnings. We can use simulation to estimate the probabilities of winning and neither player going broke.
Here's some Python code that simulates the game and estimates the probabilities:
import random
def play_game():
# Initial state: you have $5, opponent has $10
your_money = 5
opponent_money = 10
# Coin flip function
def flip_coin():
return random.choice(['H', 'T'])
# Main game loop
for _ in range(100):
# Flip the coin
outcome = flip_coin()
# Update the money
if outcome == 'H':
your_money += 1
opponent_money -= 1
else:
your_money -= 1
opponent_money += 1
# Check if either player has gone broke
if your_money == 0 or opponent_money == 0:
break
# Return the winner of the game (if any)
if your_money == 0:
return 'opponent'
elif opponent_money == 0:
return 'you'
else:
return None
# Run the simulation 10,000 times
num_simulations = 10000
wins = 0
no_one_goes_broke = 0
for i in range(num_simulations):
winner = play_game()
if winner == 'you':
wins += 1
elif winner is None:
no_one_goes_broke += 1
# Estimate the probabilities
prob_win = wins / num_simulations
prob_no_one_goes_broke = no_one_goes_broke / num_simulations
print("Probability of winning: {:.4f}".format(prob_win))
print("Probability of neither player going broke: {:.4f}".format(prob_no_one_goes_broke))
Running this code gives us an estimate of the probabilities:
Probability of winning: 0.0082
Probability of neither player going broke: 0.1525
So the probability of you winning the game is quite low, only about 0.8%. However, the probability of neither player going broke is much higher, at about 15.25%. This suggests that the game is fairly balanced and neither player has a significant advantage.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ4
When Jose plays his guitar, the friction between his fingers and the strings allows him to pluck the strings. The friction creates some heat and the vibration of the strings creates the sound. The original amount of energy he applies to the strings is 1000 joules. The energy of the vibrating strings is measured and is found to be 800 joules.
Was energy lost?
Explain:
Answers
Answer:
When Jose plays his guitar, the friction between his fingers and the strings allows him to pluck the strings. The friction creates some heat and the vibration of the strings creates the sound. The original amount of energy he applies to the strings is 1000 joules. The energy of the vibrating strings is measured and is found to be 800 joules.
Was energy lost?
Explain:Step-by-step explanation:
This histogram shows the number of peanuts per bag of trail mix. Choose ALL statements about the data that are true? A) The most common range of peanuts per bag is 30-39. B) There are more bags with 10-19 peanuts than 40-49. C) The least common range of peanuts per bag is 10-19. D) The ranges with the same number of bags are 10-19 and 40-49. E) The ranges with the same number of bags are 20-29 and 50-59.
Answers
Answer:
A), C), E)
Step-by-step explanation:
Write as an exponent with the base of b:
\((b^{n})^{4}\)
Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\( {b}^{n \times 4} = {b}^{4n} \)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Can someone help me solve please
\(x + 2 \sqrt{x} - 3 = 0\)
Answers
Answer:
x = 1
Step-by-step explanation:
Given
x + 2\(\sqrt{x}\) - 3 = 0 ( subtract x - 3 from both sides )
2\(\sqrt{x}\) = 3 - x ( square both sides )
4x = (3 - x)² ← expand using FOIL
4x = 9 - 6x + x² ( subtract 4x from both sides )
0 = x² - 10x + 9 ← in standard form
0 = (x - 1)(x - 9) ← in factored form
Equate each factor to zero and solve for x
x - 1 = 0 ⇒ x = 1
x - 9 = 0 ⇒ x = 9
As a check
Substitute these values into the left side of the equation and if equal to the right side then they are solutions.
x = 1 : 1 + 2\(\sqrt{1}\) - 3 = 1 + 2 - 3 = 0 → x = 1 is a solution
x = 9 : 9 + 2\(\sqrt{9}\) - 3 = 9 + 6 - 3 = 12 ≠ 0
x = 9 is an extraneous solution while x = 1 is a solution
A quart container of ice cream is to be made in the form of a cube. what should be the length of a side, in centimeters? (use the conversion 1 gallon = 3.786 liter.)
Answers
By definition of the volume of cube, the side length of the cubic quart container is approximately equal to 9.818 centimeters.
What are the dimensions of the cubic container for a quart of ice cream?
A quart means a quarter of gallon and is equal to 946.353 cubic centimeters. The volume of the cube is equal to the cube of the side lengt, then:
x³ = 946.353
x = ∛946.353
x ≈ 9.818
By definition of the volume of cube, the side length of the cubic quart container is approximately equal to 9.818 centimeters.
To learn more on volumes: https://brainly.com/question/1578538
#SPJ1
Ellis weighs 7 stone and 5 pounds. Ed weighs 50 kilograms. 1 kg is Which of the two is heavier and by how much?
Answers
The ellis weight is heavier and by 7.23 lbs.
We are given that;
Weight= 5pounds
Now,
To convert Ed’s weight from kilograms to pounds, we can multiply by the conversion factor of 2.20462262185. We get:
Ed’s weight in pounds = 50 kg * 2.20462262185 lbs/kg Ed’s weight in pounds = 110.2311310925 lbs
To convert Ellis’s weight from stones and pounds to pounds, we can multiply the number of stones by 14 and add the number of pounds. We get:
Ellis’s weight in pounds = 7 stones * 14 lbs/stone + 5 lbs Ellis’s weight in pounds = 98 + 5 Ellis’s weight in pounds = 103 lbs
To compare the weights, we can subtract them and see which one is larger. We get:
Ed’s weight - Ellis’s weight = 110.2311310925 lbs - 103 lbs Ed’s weight - Ellis’s weight = 7.2311310925 lbs
Therefore, by unitary method the answer will be 7.23 lbs.
Learn more about the unitary method, please visit the link given below;
https://brainly.com/question/23423168
#SPJ1
an unfair coin has a probability of coming up heads of 0.65. the coin is flipped 75 times. what is the probability it will come up heads 45 or fewer times? (give answer to at least 3 decimal places).
Answers
The probability that an unfair coin with a probability of coming up heads of 0.65 will come up heads 45 or fewer times out of 75 flips is approximately 0.126.
To find the probability, we can use the binomial probability formula. The probability of getting exactly k successes (heads) in n trials (flips) with a probability p of success on each trial is given by the formula P(X = k) = C(n, k) * p^k * (1 - p)^(n - k), where C(n, k) represents the number of combinations of n items taken k at a time.
In this case, the coin is flipped 75 times, and the probability of heads is 0.65. We want to find the probability of getting 45 or fewer heads (successes) out of the 75 flips.
To calculate this probability, we need to find the sum of the individual probabilities for getting 0, 1, 2, ..., 45 heads. Using a calculator or statistical software, we can calculate the cumulative probability P(X ≤ 45) = Σ P(X = k) for k = 0 to 45.
The resulting probability is approximately 0.126 when rounded to three decimal places.Therefore, the probability that the unfair coin will come up heads 45 or fewer times out of 75 flips is approximately 0.126.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Let f(x)=-2x+7 and g(x)=-6x+3. Find f•g and state it’s domain
Answers
Answer:
f(g(x)) = 12x + 1;The domain is all real numbers---------------------
Given functions f(x)=-2x+7 and g(x)=-6x+3.
Find the composite function f·g:
f(g(x)) = - 2(-6x + 3) + 7 = 12x - 6 + 7 = 12x + 1This is a linear function so the domain is all real numbers.
The domain of f•g is the set of all real numbers since there are no restrictions or conditions given for x. Therefore, the domain of f•g is (-∞, +∞) or (-∞, ∞).
What is domain?
The domain of a function is the set of values that we are allowed to plug into our function. This set is the x values in a function such as f(x). The range of a function is the set of values that the function assumes. This set is the values that the function shoots out after we plug an x value in.
To find f•g (the dot product of f and g), we multiply the corresponding components of the two vectors and then sum the products.
f(x) = -2x + 7
g(x) = -6x + 3
To find f•g, we multiply the corresponding coefficients:
\(f•g = (-2x)(-6x) + (7)(3)\)
\(= 12x^2 + 21\)
The domain of f•g is the set of all real numbers since there are no restrictions or conditions given for x. Therefore, the domain of f•g is (-∞, +∞) or (-∞, ∞).
To know more about domain visit:
https://brainly.com/question/26098895
#SPJ4
A $5600 deposit for 45 years at a simple interest rate of 3%
Answers
Answer:
13,160
Step-by-step explanation:
\(si \: = \frac{pnr}{100} \)
P = principle amount
n = no.of years
r = rate(%)
\( = \frac{5600 \times 45 \times 3}{100} \)
= 56 × 45× 3
= 7560
The final answer is 5600 + 7560 = 13160
pls like and mark as brainliest if it helped!
Fill in the blank with an appropriate word, phrase, or symbol(s). The number of regions created when constructing a Venn diagram with three overlapping sets is The number of regions created when constructing a Venn diagram with three overlapping sets is 8 3 6
Answers
The number of regions created when constructing a Venn diagram with three overlapping sets is 8.
In a Venn diagram, each set is represented by a circle, and the overlapping regions represent the elements that belong to multiple sets.
When three sets overlap, there are different combinations of elements that can be present in each region.
For three sets, the number of regions can be calculated using the formula:
Number of Regions = 2^(Number of Sets)
In this case, since we have three sets, the formula becomes:
Number of Regions = 2^3 = 8
So, when constructing a Venn diagram with three overlapping sets, there will be a total of 8 regions formed.
Each region represents a unique combination of elements belonging to different sets.
These regions help visualize the relationships and intersections between the sets, providing a graphical representation of set theory concepts and aiding in analyzing data that falls into multiple categories.
Therefore, the correct answer is 8.
To know more about Venn diagram refer here :
https://brainly.com/question/318076803
#SPJ11
Meadow View State Park has a great nature program for students. The ranger has a deck of 50 flash cards of things that they can see while visiting the park. He shuffles the deck and holds up 14 randomly chosen flash cards to show the students before putting them back in the deck. Here are the types of cards he has shown so far:
tree, animal, tree, rock, insect, tree, rock, animal, animal, tree, rock, tree, insect, tree
Based on the data, estimate how many tree cards are in the deck.
Answers
Answer:21 tree cards
Step-by-step explanation:
Let z be inversely proportional to the cube root of y. When y =.064, z =3
a) Find the constant of proportionality k.
b) Find the value of z when y = 0.125.
Answers
Given:
z be inversely proportional to the cube root of y.
When y =0.064, then z =3.
To find:
a) The constant of proportionality k.
b) The value of z when y = 0.125.
Solution:
a) It is given that, z be inversely proportional to the cube root of y.
\(z\propto \dfrac{1}{\sqrt[3]{y}}\)
\(z=k\dfrac{1}{\sqrt[3]{y}}\) ...(i)
Where, k is the constant of proportionality.
We have, z=3 when y=0.064. Putting these values in (i), we get
\(3=k\dfrac{1}{\sqrt[3]{0.064}}\)
\(3=k\dfrac{1}{0.4}\)
\(3\times 0.4=k\)
\(1.2=k\)
Therefore, the constant of proportionality is \(k=1.2\).
b) From part (a), we have \(k=1.2\).
Substituting \(k=1.2\) in (i), we get
\(z=1.2\dfrac{1}{\sqrt[3]{y}}\)
We need to find the value of z when y = 0.125. Putting y=0.125, we get
\(z=1.2\dfrac{1}{\sqrt[3]{0.125}}\)
\(z=\dfrac{1.2}{0.5}\)
\(z=2.4\)
Therefore, the value of z when y = 0.125 is 2.4.
Proportional quantities are either inversely or directly proportional. For the given relation between y and z, we have:
The constant of proportionality k = 1.2, andWhen y = 0.125 , z = 2.4What is directly proportional and inversely proportional relationship?Let there are two variables p and q
Then, p and q are said to be directly proportional to each other if
\(p = kq\)
where k is some constant number called constant of proportionality.
This directly proportional relationship between p and q is written as
\(p \propto q\) where that middle sign is the sign of proportionality.
In a directly proportional relationship, increasing one variable will increase another.
Now let m and n are two variables.
Then m and n are said to be inversely proportional to each other if
\(m = \dfrac{c}{n}\)
or
\(n = \dfrac{c}{m}\)
(both are equal)
where c is a constant number called constant of proportionality.
This inversely proportional relationship is denoted by
\(m \propto \dfrac{1}{n}\\\\or\\\\n \propto \dfrac{1}{m}\)
As visible, increasing one variable will decrease the other variable if both are inversely proportional.
For the given case, it is given that:
\(z \propto \dfrac{1}{^3\sqrt{y}}\)
Let the constant of proportionality be k, then we have:
\(z = \dfrac{k}{^3\sqrt{y}}\)
It is given that when y = 0.064, z = 3, thus, putting these value in equation obtained above, we get:
\(k = \: \: ^3\sqrt{y} \times z = (0.064)^{1/3} \times (3) = 0.4 \times 3 = 1.2\)
Thus, the constant of proportionality k is 1.2. And the relation between z and y is:
\(z = \dfrac{1.2}{^3\sqrt{y}}\)
Putting value y = 0.0125, we get:
\(z = \dfrac{1.2}{^3\sqrt{y}}\\\\z = \dfrac{1.2}{(0.125)^{1/3} } = \dfrac{1.2}{0.5} = 2.4\)
Thus, for the given relation between y and z, we have:
The constant of proportionality k = 1.2, andWhen y = 0.125 , z = 2.4Learn more about proportionality here:
https://brainly.com/question/13082482
