Answers
IMPORTANT THIGNS TO REMEMBER:
Has 20 lb. dog food!Gives dog 1 3/5 everyday!Find how much eaten after 2 days!Find how much is left!ANSWER:
Dog has eaten 3 1/5 after 2 days!
There is 16 4/5 left in bag!
EXPLANATION:
Since she gives 1 3/5 to her dog everyday and their asking for 2 days you would multiply 1 3/5 × 2 OR add 1 3/5 + 1 3/5
Which would give you 3 1/5
So, the dog has eaten 3 1/5 lb. of dog food in 2 days.
However then, you would subtract 20 lb. - 3 1/5 lb. because there is 20 lb. dog food in all and the dog has eaten 3 1/5 of it. This would give you 16 4/5 lb.
Meaning there is 16 4/5 lb. left in the bag of dog food!
Related Questions
an experiment has only two outcomes. the first has probability p to occur, the second probability p2. what is p?
Answers
Solution:
Probability of the second outcome occurring is 1-p
Explanation:
In an experiment with only two outcomes, the probabilities of both outcomes must add up to 1.
This means that if the first outcome has a probability of p, the second outcome must have a probability of 1-p.
Therefore, the equation for this situation would be: p + (1-p) = 1Solving for p, we get: p = 1 - (1-p) = 1 - 1 + p = p.
Therefore, the probability of the first outcome occurring is simply p, as given in the question.
The probability of the second outcome occurring is 1-p.
To know more about the probability refer here:
https://brainly.com/question/30034780#
#SPJ11
The probability of the first outcome, p, is equal to the total probability of all outcomes, minus the probability of the second outcome, p2. So, p = 1 - p2.
In an experiment with only two outcomes, the sum of the probabilities of the two outcomes must equal 1. This means that if the first outcome has a probability of p, the second outcome must have a probability of 1-p.
Therefore, the probability of the first outcome, p, can be found by subtracting the probability of the second outcome, p2, from 1:
p = 1 - p2
So, if you know the probability of the second outcome, you can find the probability of the first outcome by subtracting it from 1.
For example, if the probability of the second outcome is 0.3, the probability of the first outcome would be:
p = 1 - 0.3 = 0.7
So the probability of the first outcome is 0.7.
Know more about probability here:
https://brainly.com/question/13604758
#SPJ11
Find the type and number of roots of the following equations using the discriminat

Answers
Recall that the discriminant of a quadratic equation:
\(ax^2+bx+c=0\)is:
\(\Delta=b^2-4ac\text{.}\)Also, if:
\(\begin{cases}\Delta>0\text{ the quadratic equation has 2 different real roots,} \\ \Delta=0\text{ the quadratic equation has 1 root of }multiplicity\text{ 2,} \\ \Delta<0\text{ the quadratic equation has 2 different imaginary roots.}\end{cases}\)Now, notice that the discriminant of the given equation is:
\(\Delta=4^2-4\cdot1\cdot(-2)\text{.}\)Simplifying the above result we get:
\(\Delta=16+8=24.\)Since 24>0, we get that the given equation has 2 different real roots.
Answer: The given equation has 2 different real roots.
A can of soda can be modeled as a right cylinder. Noah measures its height as 9. 2 cm and its radius as 2. 6 cm. Find the volume of the can in cubic centimeters. Round your answer to the nearest tenth if necessary.
Answers
So, the volume of the can in cubic centimeters is 61.99 cm^3. If we round to the nearest tenth, the volume of the can is 62 cm^3.
A can of soda can be modeled as a right cylinder, which is a three-dimensional geometric shape with two circular bases that are connected by a curved surface. The volume of a cylinder can be calculated using the formula:
V = πr^2h
Where V is the volume, π is a constant (approximately equal to 3.14), r is the radius of the base and h is the height of the cylinder.
Given that the radius of the can is 2.6 cm and the height is 9.2 cm, we can substitute these values into the formula:
V = π (2.6 cm)^2 (9.2 cm)
To get the area of the base we need to square the radius and multiply by π, and then multiply it by the height to get the volume.
V = π * 6.76 * 9.2 = 61.99 cm^3
So the volume of the can in cubic centimeters is 61.99 cm^3. If we round to the nearest tenth, the volume of the can is 62 cm^3. This means that the can can hold 62 cubic centimeters of liquid.
It's worth noting that this is an approximation and the real value of π is not 3.14. Also, this answer is based on the assumption that the can is a perfect cylinder with no other gaps or spaces.
To learn more about Volume of figures
visit; brainly.com/question/10184308
#SPJ4
What is the slope of the line and y intercept

Answers
You need to find the y-intercept (aka b). You can do that by simply looking where the graph intercepts with the Y-axis.
b= 1 (positive 1 and not negative)
Now we need to find the slope by the following
Slope aka m: (Y2-Y1)/(X2-X1)
Note: sometimes people say it’s rise/run which is the same thing as the previous formula.
Pick two points that fall on the graph. I chose (0,1) and (3,-4). Even though there are no numbers you can assume each square is a unit and count the squares.
Slope = (-4-1)/(3-0) = - 5/3
Region of quipped random samples of 56 Mel and 56 female students from a large university with a small device that secretly record sound for a random 30 seconds during each 12.5 minute period over two days then they counted the number of words spoken by each subject during each recording. From this estimate how long many words per day each student speaks the female estimates had a mean of 16,177 words per day with a standard deviation of 7520 words per day. For the mail estimate the mean was 16,569 and Santa deviation was 9108 do these data provide convincing evidence at 0.05 significance level of a difference in the average number of words spoken in a day but all males and female student at this university
Answers
Based on the given data, there is not enough evidence to suggest a significant difference in the average number of words spoken per day between male and female students at this university at a significance level of 0.05.
How to calculate the valueThe critical value will be:
= ✓(55)(7520²) + (55)(9108²))/(56 + 56 - 2))
≈ 8285.89
t = (16177 - 16569) / (8285.89 * ✓(1/56 + 1/56))
≈ -0.4704
The critical value for a two-tailed test with α = 0.05 and df = 110 is approximately ±1.983.
Since the absolute value of the test statistic (0.4704) is less than the critical value (1.983), we fail to reject the null hypothesis.
Therefore, based on the given data, there is not enough evidence to suggest a significant difference in the average number of words spoken per day between male and female students at this university at a significance level of 0.05.
Learn more about hypothesis on
https://brainly.com/question/11555274
#SPJ1
Dante deposited $5,000 into an account with an annual interest rate of
3.5%. He plans to deposit an additional $200 each year, just after the
interest is compounded. What will his balance be after 16 years? (round to
the penny)
Answers
Dante deposited $5,000 into an account with an annual interest rate of
3.5%. He plans to deposit an additional $200 each year, just after the
interest is compounded. His balance will be $9,838.44 after 16 years.
What do you mean by annual interest rate?It displays the actual percentage rate of interest owed on any outstanding debts, including credit card debt and loans.
Because it takes compounding effects into account, the effective annual interest rate is the real interest rate on an investment or loan. The rate increases as the compounding periods get more frequent. Advertisements for loans or savings accounts may include both the nominal interest rate and the effective yearly interest rate. The rate that should be used to compare loan and investment rates of return is the effective annual interest rate.
We can substitute the known values into the formula and calculate the final balance:
A = $5,000 (1 + 0.035)¹⁶
We can calculate the final balance by using a calculator, or we can use the formula of compound interest:
A = P(1 + r/n)ˣ
where, A= Amount
P= Principle($5,000 )
x= Time(16 years)
n= Rate(3.5%)
A = $5,000 (1 + 0.035/1)¹⁶
Now we can add the $200 deposit each year for 16 years:
A = $5,000 (1 + 0.035)¹⁶ + $200 × 16
A = $9,838.44
Dante's balance will be $9,838
To know more about interest visit:
https://brainly.com/question/29480777
#SPJ1
a bowl of kashi cereal has 25 grams of total carbohydrates of which 4g is fiber, and 1 gram of fat, how many total calories does it have?
Answers
The bowl of Kashi cereal has a total of 93 calories
Each gram of carbohydrates provides 4 calories, and each gram of fat provides 9 calories. To calculate the total calories in the bowl of Kashi cereal, we need to determine the calories from carbohydrates and fat separately and then add them together.
Calories from carbohydrates
Total carbohydrates = 25g
Fiber = 4g
Net carbohydrates = Total carbohydrates - Fiber = 25g - 4g = 21g
Calories from carbohydrates = Net carbohydrates x 4 calories/gram
Calories from carbohydrates = 21g x 4 calories/gram
Calories from carbohydrates = 84 calories
Calories from fat
Fat = 1g
Calories from fat = Fat x 9 calories/gram
Calories from fat = 1g x 9 calories/gram
Calories from fat = 9 calories
Total calories = Calories from carbohydrates + Calories from fat
Total calories = 84 calories + 9 calories
Total calories = 93 calories
Learn more about calories here
brainly.com/question/7648892
#SPJ4
whats 78,563 divided by 98
Ty for whoever helps me <3
Answers
Answer:
801.66
Step-by-step explanation:
calculator
Answer:
801.6632653061
Step-by-step explanation:
.......
What is the value of n in the equation 2.3 × 10^9 = (1 × 10^3)(2.3 × 10n)?
Answers
By using the quotient of powers property, we will see that the value of n must be 6.
What is the value of n in the equation?Here we want to solve the equation below:
2.3 × 10^9 = (1 × 10^3)(2.3 × 10^n)
For the exponent n.
To fo so, we can start by dividing both sides by the first factor on the right side.
2.3 × 10^9 = (1 × 10^3)(2.3 × 10^n)
(2.3× 10^9)/(1 × 10^3) = 2.3 × 10^n
Remember the quotient between powers of the same base:
a^n/a^m = a^{n - m}
Then we will get:
(2.3× 10^9)/(1 × 10^3) = 2.3 × 10^n
(2.3/1)×(10^9/10^3) = 2.3 × 10^n
Now we can use the property written above:
2.3×10^{9 - 3} = 2.3 × 10^n
2.3×10^6 = 2.3×10^n
There we can see that the value of n must be 6.
Learn more about exponents:
https://brainly.com/question/847241
#SPJ1
Help please thankyou in advance

Answers
Answer:
degree is 2
standard form is
-x^2+2x-8
classification is trinomial
leading coeff is -1
hope i helped
Step-by-step explanation:
Plzzzzz Help!!!!Find an equation for the perpendicular bisector of the line segment whose endpoints are (8,4) and (4,-4)

Answers
Answer:
y = 2x -12 to find any equation to the perpendicular line x=0
Step-by-step explanation:
find the slope to the original line using the slope formula , then take the opposite reciprocal = -1/2
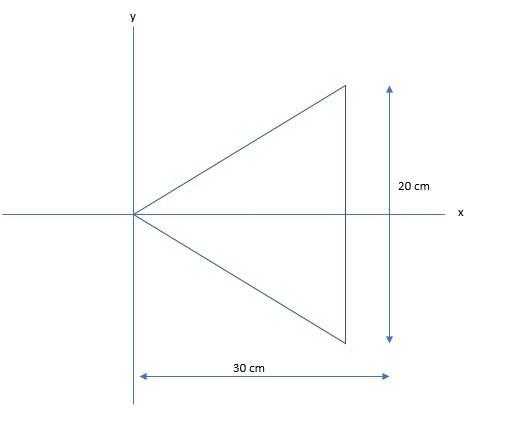
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

Use power series to evaluate the following:
15a) n=0 (-1)² 7³² (2n)!9" 2n+1 15b) (−1)" 3+¹ 00 n=0n!5"- 15c) √ x³ sin(x²)dx
Answers
15a) To evaluate the power series ∑((-1)^(2n) * 7^(32) * (2n)! * 9^(2n+1)), we can break it down term by term.
The term can be written as follows:
((-1)^(2n) * 7^(32) * (2n)! * 9^(2n+1))
Let's start evaluating each part of the term:
1. (-1)^(2n) = 1 for all values of n, since any even power of -1 is 1.
2. 7^(32) is a constant term that remains the same for all values of n.
3. (2n)! represents the factorial of 2n. It is the product of all positive integers from 1 to 2n.
4. 9^(2n+1) can be simplified as (9^2)^n * 9. Since (9^2) is a constant, it remains the same for all values of n.
Now, let's substitute these values back into the power series:
∑((-1)^(2n) * 7^(32) * (2n)! * 9^(2n+1))
= ∑(1 * 7^(32) * (2n)! * (9^2)^n * 9)
The series can be simplified further by factoring out the constants:
= 7^(32) * 9 * ∑((2n)! * (9^2)^n)
Now we have a power series in the form of ∑(c * a^n), where c and a are constants. We can use the properties of power series to evaluate it.
However, it seems that there might be a typo in the given expression as the factorial term (2n)! and the exponent of 9^(2n+1) both have an odd power of 2n. Please verify and provide the correct expression if there is a mistake.
15b) To evaluate the power series ∑((-1)^n * 3^(n+1) * (n!)^2 / 5^n), we can follow a similar approach.
The term can be written as follows:
((-1)^n * 3^(n+1) * (n!)^2 / 5^n)
1. (-1)^n alternates between 1 and -1 for even and odd values of n, respectively.
2. 3^(n+1) is a constant term that changes as n increases.
3. (n!)^2 represents the square of the factorial of n.
4. 5^n is a constant term that remains the same for all values of n.
Now, let's substitute these values back into the power series:
∑((-1)^n * 3^(n+1) * (n!)^2 / 5^n)
= ∑((-1)^n * 3^(n+1) * (n!)^2 * (5^-1)^n)
Simplifying further:
= ∑((-1)^n * 3^(n+1) * (n!)^2 * (1/5)^n)
Now we have a power series in the form of ∑(c * a^n), where c and a are constants. We can use the properties of power series to evaluate it.
15c) To evaluate the integral of √(x^3) * sin(x^2) dx using power series, we can expand the function sin(x^2) as a power series.
To know more about convergence visit-
brainly.com/question/31968534
#SPJ11
Please answer this for me ASAP
Which number is nearest in value to 7508.
A. 5,706
B. 6,993
C. 8,108
D. 8,522
E. 1,050
Answers
Step-by-step explanation:
Let's find the difference between 7508 and the other numbers.
A. 5706 - 7508 = -1802
B. 6993 - 7508 = -515
C. 8108 - 7508 = 600
D. 8522 - 7508 = 1014
E. 1050 - 7508 = -6458
If we do not take +ve / -ve into account,
the closest number to 7508 = the smallest difference
which in this case, is B, 6993.
Answer:
B. 6993
Step-by-step explanation:
hope this helps :)
An arithmetic sequence k starts 4, 13,. Explain how you would calculate the value of the 5,000th term
Answers
The value of the 5000th term is 44995.
Given, an arithmetic sequence k starts 4, 13, and we are required to calculate the value of the 5,000th term. Arithmetic sequence: An arithmetic sequence is a sequence in which each term is equal to the previous term plus a constant value, known as the common difference, denoted by d.
Formula: The nth term in an arithmetic sequence is given by the formula: `an=a1+(n-1)d`Here,a1 = 4, d = 13 - 4 = 9We need to find the 5000th term, so n = 5000.Therefore, the value of the 5000th term, an is given by:an = a1 + (n - 1)d= 4 + (5000 - 1)9= 4 + 44991= 44995
Know more about arithmetic sequence here:
https://brainly.com/question/15456604
#SPJ11
How much parent nuclide remains after three half-lives have elapsed? A. 0% B. 6.25% C. 12.5% D. 30% 29. If a sample of radioactive material contains 17% daughter nuclide, what percentage of parent nuclide is present in the sample? A. 0% B. 17% C. 50% D. 83% 30. The isotope used to determine the absolute age of organic remains is A. carbon-14 B. carbon-12 C. uranium-235 D. uranium-238 31. The half-life of carbon-14 is 5730 years. How old is a bone fragment if the proportion of carbon-14 remaining is 25%? A. 2865 a B. 5760 a C. 11 460 a D. 17 190 a
Answers
Answer:
In order of the questions asked, the answers are, C, D, A, C
Step-by-step explanation:
After three half-lives have elapsed, 12.5% of the original nuclide remains, so the answer is C.
if 17 % is daughter nuclide, then 83% is parent nuclide, so , the answer is D
the isotope for dating organic remains is A. carbon-14
for 25% of original, 2 half-lives must have passed, so we get (2)(5730) = 11460
so the answer is C
hi i’m gonna need some help on this i don’t understand at all

Answers
Let's begin by finding the mean of the data
\(\begin{gathered} \text{Mean = }\frac{\sum x}{n}=\text{ }\frac{46\text{ + 47 + }5\text{6 + 48 + }46\text{ + 52 + }5\text{7 + 52 + 4}5}{9} \\ \text{Mean = }\frac{449}{9}=48.89\text{ }\approx\text{ 48.9} \end{gathered}\)Mean = 48.9
Next, we calculate the absolute value of the difference between each data value and the mean, we have:
|data value – mean|
|46 - 48.9| = 2.9
|47 - 48.9| = 1.9
|56 - 48.9| = 7.1
|48 - 48.9| = 0.9
|46 - 48.9| = 2.9
|52 - 48.9| = 3.1
|57 - 48.9| = 8.1
|52 - 48.9| = 3.1
|45 - 48.9| = 3.9
Next, we sum up the absolute values of the differences (from above) & divide by the number of data values, we have:
\(\begin{gathered} MOD=\frac{2.9\text{ + 1.9 + 7.1 + 0.9 + 2.9 + 3.1 + 8.1 + 3.1 + 3.9}}{9}=\frac{69}{9} \\ \text{MOD = 7.7 }\approx\text{ 8 (to the nearest whole number)} \end{gathered}\)MOD = 8 (to the nearest whole number)
Write an equation in slope-intercept form of a line passing through the given point andparallel to the given line.13. (4, 2); x+ y= 1

Answers
The equation of the line in slope-intercept form is,
\(y=mx_{}+b\)where,
m = slope
The equation of the line given is,
\(x+y=1\)Let us now rearrange the equation in the slope-intercept form in order to obtain the slope.
Therefore,
\(\begin{gathered} x+y=1 \\ y=-x+1 \\ \therefore\text{ The slope(m) is -1.} \end{gathered}\)We were told the point is parallel to the equation of the line.
The rule for parallelism is,
\(\begin{gathered} m_1=m_2 \\ \therefore-1=-1 \end{gathered}\)The formula to calculate for the equation of a line given one point is,
\(y-y_1=m(x-x_1)\)Given
\(\begin{gathered} (x_1,y_1)=(4,2) \\ m=-1 \end{gathered}\)Substitute and simplify
\(\begin{gathered} y-2=-1(x-4) \\ y-2=-1x+4 \\ y=-x+4+2 \\ \therefore y=-x+6 \end{gathered}\)Hence, the equation of the line in slope-intercept form is
\(y=-x+6\)Drag each tile to the correct box.
Arrange the steps to perform this subtraction operation in the correct order.
(1.93 × 107) − (9.7 × 106)
1: (1.93 x 10^7) - (9.7 x 10^6)
2: 0.96 x 10^7
3: (1.93 x 10^7) - (0.97 x 10^7)
4: 10/10 (0.96 x 10^7)
6: (1.93 - 0.97) x 10^7
7: (1.93 x 10^7) - 10/10 (9.7 x 10^6)
8: 9.6 x 10^6
Answers
Answer:
A, D, C, F, B, G
Step-by-step explanation:
The correct order of the given expressions is:
1: (1.93 x 10⁷) - (9.7 x 10⁶)
3: (1.93 x 10⁷) - (0.97 x 10⁷)
6: (1.93 - 0.97) x 10⁷
2: 0.96 x 10⁷
4: 10/10 (0.96 x 10⁷)
7: (1.93 x 10⁷) - 10/10 (9.7 x 10⁶)
8: 9.6 x 10⁶
What is an expression?In mathematics, an expression is a combination of one or more numbers, variables, and mathematical operations that can be evaluated to produce a value or result.
The correct order to perform the subtraction operation is:
Write out the problem: (1.93 x 10⁷) - (9.7 x 10⁶)
Subtract the second number from the first number (ignoring the scientific notation): (1.93 - 0.97) x 10⁷
Simplify the subtraction to get the result in scientific notation: 0.96 x 10⁷. Convert the result to standard scientific notation: 9.6 x 10⁶.
To know more about an expression follow
https://brainly.com/question/29201136
#SPJ2
In one-way ANOVA, involving three groups, the alternative hypothesis would be considered correct if, in the population,a.all means were equalb.two means are equal but the third is differentc.all three means have different valuesd.either (b) or (c) above is true
Answers
There are at least two group means that are significantly different from one another, according to the alternative hypothesis (H a). The alternative hypothesis is adopted if the outcome is statistically significant.
What is anova test?You can use ANOVA to determine whether differences between data sets are statistically significant. It functions by examining the levels of variance present within each group using samples drawn from each.
The likelihood that the mean of a sample taken from the data will be different owing to chance increases if there is a lot of variance (spread of data away from the mean) among the data groups.
In addition to examining the variance within the data groups, ANOVA also considers sample size (the smaller the sample, the lower the likelihood that outliers will be randomly selected from it) and sample mean differences (the greater the difference between the sample means, the greater the likelihood that an outlier will be randomly selected from it).
hence, The alternative hypothesis is adopted if the outcome is statistically significant.
learn more about anova test click here:
https://brainly.com/question/25800044
#SPJ4
60 points (3 different questions) INEQUALITIES AND EQUALITY SOLVING
-6(1+7x)+7(1+6x)=-2 (I got no solution but I want to make sure that's correct)
-2(2-2x)-4(x+5)≤ -24 (I think I got the answer but I have no clue how to do this on a number line)
-2(5+6n)<6(8-2n) (I think I got the answer but no clue on the number line)
I will mark the best answer but there is a 24-hour time limit!
Answers
Answer:
1. No solution
2. All real numbers
3. Always true
Step-by-step explanation:
Answer: look at the picture and you will see the answer, for the numbers 3 -2(5+6n)<6(8-2n) it all real numbers are solutions.
Step-by-step explanation: hope this help


What is the area of the trapezoid if the bottom base is 4x-5 and the top is 6x+3 with both sides being -5x+10?
Answers
Step-by-step explanation:
Area=(a+b)/2 x h
a=6x+3
b=4x-5
h=-5x+10
Area= -25x^2+55x-10
Fill in the blanks with the answer to each question based on information provided.Two toy robots are having a race. Robot A can go 14 meter in 15 seconds. Robot B can go 1 meter in 50 seconds.1) If Robot A continues at that same speed, how long will it take to go 1 meter? Remember units! __________2) How long for Robot A to go 4 meters at that speed? Remember units! _________
Answers
Answer:
1 1/14 seconds4 2/7 secondsStep-by-step explanation:
We are being asked for times, so we can express the rate in terms of seconds per meter.
(15 seconds)/(14 meters) = (15/14) seconds per meter = 1 1/14 seconds/meter
__
1) It will take Robot A 1 1/14 seconds to go 1 meter.
2) it will take Robot A 4 2/7 seconds to go 4 meters. (4 times as long)
Patrice earns $10 per hour.
Last week, she worked 9
hours on Monday, 3 hours
on Tuesday, and 8 hours on
Wednesday She had
Thursday off, and then she
worked 6 hours on Friday.
How much money
did
Patrice earn in all last week?
Answers
Answer:
She earned 260 dollars
Step-by-step explanation:
If you multiply 9 by 10 you get 90 then do the same to the rest of the numbers then add them you get your answer.
HELPPPP (x-y)^3-(y-x)^2
Answers
Answer:
(x-y)(x-y)(x-y)= x²-yx+x²-yx-yx+y²-yx+y²
2x²-4yx+2y²
(y-x)(y-x)= y²-yx-yx+x²
y²-2yx+x²
-(y²-2yx+x²) = -y²+2yx-x²
2x²-4yx+2y²-y²+2yx-x²= x²-2yx+y²
or
(x−y−1)(x−y)² ≡ x³−x²+3xy²+2xy−y³−y²−3yx³
students who score within 22 points of the number 78 will pass a particular test. write this statement using absolute value notation and use the variable x for the score.
Answers
The statement using absolute value notation will be x - 78 ≤ 22.
The student will pass the test which scores 22 points for the number 78
Absolute values are any digit's value without taking the sign into an account. Therefore, all negative numbers will be regarded as positive for absolute value. The absolute value of -5, for instance, will be 5, whereas that of -7, will be 7.
In essence, the absolute value calculates the distance from zero. Putting an absolute value on something does not imply that they are the same number but that they are the same distance from 0.
Le the score of student be = x
Forming the absolute value notation -
This can be expressed as,
x - 78 ≤ 22.
Read more about absolute value notation on:
https://brainly.com/question/24504417
#SPJ4
HELP PLEASE ITS MY LAST QUESTION!!
Jonathan and his band want to record and sell CDs. The recording studio charges an initial set-up fee of $250, and it charges $6.00 to burn each CD.
a) Define the variables:
Let n = _______
Let C = _______
Answers
Answer:
N=CD C=2-3 sentance
Step-by-step explanation:
when waves travel through water, why do the moving water particles continue to return to their starting point?
Answers
Answer:
Waves transfer energy, but not matter.
Waves transfer energy from one point to another without moving matter.
i hoped this helped
if marvin cannon completed 81 successful free throws put of 90 attempts what percent were unsuccessful
Answers
Total attempt = 90
Successful throws = 81
Unsuccessful = Total attempt - Successful
= 90 - 81
=> 9
To calculate the percentage of unsuccessful, we will use the formula:
\(undefined\)PLZ HELP ME I HAVE 5 MORE MINUTES

Answers
Answer:
-10
Step-by-step explanation:
-5(2) - 4(-1) - 8 +2(2)
Answer:
-10
Step-by-step explanation:
-5(2)-4(-1)-8+2(2)=
-10+4-8+4=-10
-×- is +
-×+ is -
