Answers
Related Questions
Find the equation of the line that passes through the point (3,-5) and has a slope of -1
A. y - 5 = -1 (x + 3)
B. y + 3 = -1 (x + 5)
C. y - 3 = - (x - 5)
D. y + 5 = - (x - 3)
Answers
Answer:
excfvgbhnj
Step-by-step explanation:
D. y + 5 = - (x - 5 )
Find the length of side x in simplest radical form with a rational denominator.
60
х
309
2

Answers
Answer:
\(\frac{2}{3} \sqrt{3}\)
Step-by-step explanation:
We know this triangle has angles 30, 60, and 90 degrees. Triangles with these angles have a special relationship on the sides.
The side opposite to the 90 degree angle is 2 times of x.
The side opposite to the 60 degree angle is \(\sqrt{3}\) multiplied x.
We know the side opposite to 60 degree angle is 2, so x would be
\(\frac{2}{\sqrt{3}}\)
However, we can't have an irrational number in the demoninator so we multiply the fractice by root 3 over root 3:
\(\frac{2}{\sqrt{3}} * \frac{\sqrt{3}}{\sqrt{3}}\)
which gives us \(\frac{2}{3} \sqrt{3}\)

What is the solution to the inequality below? x2 < 36
a. -6 x 6
b. x -6 or x 6
c. x < -6 or x > 6
d. -6 < x < 6
Answers
The solution to the inequality \(x^2\) < 36 is x < -6 or x > 6. Therefore, option c. is correct.
To solve the inequality \(x^2\) < 36, we can start by subtracting 36 from both sides to obtain \(x^2\)- 36 < 0. Next, we can factor the left side as (x - 6)(x + 6) < 0. Since the product of two numbers is negative when one of the numbers is positive and the other is negative, we have two possibilities:
(x - 6) < 0 and (x + 6) > 0: This implies x < 6 and x > -6, which means x is greater than -6 and less than 6.
(x - 6) > 0 and (x + 6) < 0: This implies x > 6 and x < -6. However, this condition is not possible since it contradicts the first possibility.
Therefore, the solution to the inequality \(x^2\)< 36 is x < -6 or x > 6, which is option (c) in the given choices.
Learn more about inequality here:
https://brainly.com/question/28823603
#SPJ11
a triangle has sides of 12,36,37 is this a right triangle
Answers
The triangle has sides of 12, 36, and 37 and is not a right triangle.
What are Pythagoras's triples of the right triangle?
Pythagorean triples are defined as a² + b² = c², where a, b, and c are positive integers. These triples are denoted as (a,b,c). The perpendicular is a the base is b, and the hypotenuse is c of a right-angled triangle.
We have,
a triangle has sides of 12, 36, 37
A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c². Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k.
(12)² + (36)² = (37)²
1440 = 1369
S0, LHS ≠ RHS
Hence, the triangle has sides of 12, 36, and 37 is not a right triangle.
To learn more about Pythagoras's triples visit,
https://brainly.com/question/16036846
#SPJ1
Consider the initial value problem
dt
dx
=[
3
3
−3
3
]x,x(0)=[
5
5
] (a) Find the eigenvalues and eigenvectors for the coefficient matrix. λ
1
=,
v
1
=[,,,,,,[ (b) Solve the initial value problem. Give your solution in real form. x(t)=[ Use the phase plotter pplane9.m in MATLAB to answer the following question. . Describe the trajectory.
Answers
a. the eigenvalues are: λ1 = (√3 + 1) / √3, λ2 = (√3 - 1) / √3 , b. where c1 and c2 are constants determined by the initial condition x(0) = [5/√5 5/√5]^T. The phase plotter pplane9.m in MATLAB can be used to visualize the trajectory of the solution, but I'm unable to provide the specific trajectory without the numerical values of the eigenvalues and eigenvectors.
To solve the initial value problem, we need to find the eigenvalues and eigenvectors of the coefficient matrix. Let's start by finding the eigenvalues λ and eigenvectors v.
(a) Finding eigenvalues and eigenvectors:
The coefficient matrix is:
[ 3/√3 -3/√3 ]
[ 3/√3 3/√3 ]
To find the eigenvalues, we solve the characteristic equation:
det(A - λI) = 0
where A is the coefficient matrix, λ is the eigenvalue, and I is the identity matrix.
For the given coefficient matrix, the characteristic equation becomes:
(3/√3 - λ)(3/√3 - λ) - (-3/√3)(3/√3) = 0
Simplifying the equation:
(3/√3 - λ)^2 - 1 = 0
(3 - √3λ)^2 - 1 = 0
Expanding and rearranging:
9 - 6√3λ + 3λ^2 - 1 = 0
3λ^2 - 6√3λ + 8 = 0
Using the quadratic formula:
λ = (-(-6√3) ± √((-6√3)^2 - 4(3)(8))) / (2(3))
λ = (6√3 ± √(108 - 96)) / 6
λ = (6√3 ± √12) / 6
λ = (√3 ± 1) / √3
So, the eigenvalues are:
λ1 = (√3 + 1) / √3
λ2 = (√3 - 1) / √3
Next, we find the eigenvectors corresponding to each eigenvalue:
For λ1 = (√3 + 1) / √3:
To find the eigenvector v1, we solve the equation (A - λ1I)v1 = 0, where I is the identity matrix.
Substituting the values:
[ 3/√3 - (√3 + 1) / √3 -3/√3 ]
[ 3/√3 3/√3 - (√3 + 1) / √3 ]
Simplifying and setting it equal to zero:
[ 2/√3 - (√3 + 1) / √3 -3/√3 ]v1 = 0
[ 3/√3 2/√3 - (√3 + 1) / √3 ]v1 = 0
Simplifying further:
[ -1/√3 - (√3 + 1) / √3 -3/√3 ]v1 = 0
[ 3/√3 -1/√3 - (√3 + 1) / √3 ]v1 = 0
This system of equations can be solved to find the eigenvector v1.
Similarly, for λ2 = (√3 - 1) / √3:
To find the eigenvector v2, we solve the equation (A - λ2I)v2 = 0, where I is the identity matrix.
Substituting the values:
[ 3/√3 - (√3 - 1) / √3 -3/√3 ]
[ 3/√3 3/√3 - (√3 - 1) / √3 ]
Simplifying and setting it equal to zero:
[ 2/√3 - (√3 - 1) / √3 -3/√3 ]v2 = 0
[ 3/√3 2/√3 - (√3 - 1) / √3 ]v2 = 0
Simplifying further:
[ -1/√3 - (√3 - 1) / √3 -3/√3 ]v2 = 0
[ 3/√3 -1/√3 - (√3 - 1) / √3 ]v2 = 0
This system of equations can be solved to find the eigenvector v2.
(b) Solving the initial value problem:
To solve the initial value problem, we use the eigenvalues and eigenvectors obtained in part (a).
The general solution to the initial value problem is given by:
\(x(t) = c1 * e^(λ1 * t) * v1 + c2 * e^(λ2 * t) * v2\)
where c1 and c2 are constants determined by the initial condition x(0) = [5/√5 5/√5]^T.
Substituting the values of λ1, v1, λ2, and v2 into the general solution, we get the specific solution for the initial value problem.
The phase plotter pplane9.m in MATLAB can be used to visualize the trajectory of the solution, but I'm unable to provide the specific trajectory without the numerical values of the eigenvalues and eigenvectors.
Learn more about trajectory
https://brainly.com/question/88554
#SPJ11
What is the size of an angle called a revolution
Answers
Answer:
Step-by-step explanation:
The size of the angle of one whole revolution is 360 degrees. A revolution describes the angle of a circular surrounding sector as it rotates! This means one full revolution is 360 degrees. And half of a revolution is 180 degrees!
1. An Estate dealer sells houses and makes a commission of GHc3750 for the first house sold. He
receives GHc500 increase in commission for each additional house sold. How many houses must
she sell to reach a total commission of GHc6500?
Answers
If an Estate dealer sells houses and makes a commission of GHc3750 for the first house sold and receives GHc500 increase in commission for each additional house sold, for reaching a total commission of GHc6500, she must have sold 6.5 houses.
How is the number of houses sold determined?The number of houses the estate dealer sold to reach a total commission of GHc6500 can be determined using the mathematical operations of subtraction, division, and addition.
The total commission received = GHc6,500
The commission for the first house = GHc3,750
The commission for the remaining houses sold = GHc2,750 (GHc6,500 - GHc3,750)
The commission for additional sale of each house = GHc500
The number of additional houses sold = 5.5 (GHc2,750/GHc500)
The total number of houses sold = 6.5 (5.5 + 1 or the first house)
Learn more about sales commissions at https://brainly.com/question/24951536.
#SPJ1
Find the Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) for the curve →r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0. Round answers to 3 decimal places.
T(0) =0=[sqrt(89)= sqrt(89)]
N(0) =[ ]
B(0) =[ ]
Answers
The tangent vector → \(r(t)=〈4cos(2t),4sin(2t),5t〉\), normal vector at t=0 is given by →N(0) = 〈-1,0,0〉, and binormal vector at t=0 is given by →\(B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector, normal vector, and binormal vector of the given curve are as follows:
Given curve:
→ \(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0
To find: Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) at the point t=0
Tangent vector: To find the tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0,
we need to differentiate the equation of the curve with respect to t.t = 0, we have:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉→r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
Differentiating w.r.t t:→\(r(t) = 〈4cos(2t),4sin(2t),5t〉 → r'(t) = 〈-8sin(2t),8cos(2t),5〉t = 0\),
we have:
→\(r'(0) = 〈-8sin(0),8cos(0),5〉= 〈0,8,5〉\)
Therefore, the tangent vector at t = 0 is given by
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Normal vector:To find the normal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to differentiate the equation of the tangent vector with respect to t.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating w.r.t t:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉t = 0\),
we have:
→\(T'(0) = 〈-16cos(0),-16sin(0),0〉= 〈-16,0,0〉\)
Therefore, the normal vector at t = 0 is given by
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Binormal vector: To find the binormal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to cross-product the equation of the tangent vector and normal vector of the curve.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉\)
The cross product of two vectors:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the binormal vector at t = 0 is given by→B(0) = 〈0, -0.441, -0.898〉
Hence, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are as follows:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The given curve is
→\(r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0.\)
We are asked to find the tangent vector, the normal vector, and the binormal vector of the given curve at t=0.
the tangent vector at t=0. To find the tangent vector, we need to differentiate the equation of the curve with respect to t. Then, we can substitute t=0 to find the tangent vector at that point. the equation of the curve Is:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉\)
At t = 0, we have:
→\(r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
We can differentiate this equation with respect to t to get the tangent vector as:
→\(r'(t) = 〈-8sin(2t),8cos(2t),5〉\)
At t=0, the tangent vector is:
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Next, we find the normal vector. To find the normal vector, we need to differentiate the equation of the tangent vector with respect to t. Then, we can substitute t=0 to find the normal vector at that point.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating this equation with respect to t, we get the normal vector as:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉\)
At t=0, the normal vector is:
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Finally, we find the binormal vector. To find the binormal vector, we need to cross-product the equation of the tangent vector and the normal vector of the curve.
At t=0, we can cross product →T(0) and →N(0) to find the binormal vector.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
The normal vector is:
→N(0) = 〈-1,0,0〉Cross product of two vectors →T(0) and →N(0) is given as:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0 is given by →\(T(0) = 〈0.000,0.898,0.441〉.\)
The normal vector at t=0 is given by →N(0) = 〈-1,0,0〉.
The binormal vector at t=0 is given by →B(0) = 〈0, -0.441, -0.898〉.
To know more about binormal vectors visit
brainly.com/question/31673319
#SPJ11
Like other birds, emperor penguins use their lungs to
breathe air. Emperor penguins hunt for fish, squid,
and other food underwater. When an emperor
penguin dives into the water, it can hold its breath for
as long as 20 minutes.
What happens to the air that an emperor penguin breathes in? Select all that apply.
The air travels through passageways to all parts of the body.
In the lungs, oxygen from the air is absorbed into the blood.
The air travels through passageways to the lungs.
Answers
need help por favor
2. (8 pts.) Differentiate. Simplify your answer as much as possible. Write your answer with positive exponents only. HINT: Use Properties of Logarithms. h(x) = -17 + e²-12 + 4 155 -e-³x + ln(²+3) 5
Answers
The derivative of h(x) is h'(x) = e²-12 + 3e^(-³x) + 2/(5(²+3)), and this is the simplified answer.
To differentiate the function h(x) = -17 + e²-12 + 4/155 - e^(-³x) + ln(²+3)/5, we will use the properties of logarithms and the rules of differentiation. Let's break down the function and differentiate each term separately:
The first term, -17, is a constant, and its derivative is 0.
The second term, e²-12, is a constant multiplied by the exponential function e^x. The derivative of e^x is e^x, so the derivative of e²-12 is e²-12.
The third term, 4/155, is a constant, and its derivative is 0.
The fourth term, e^(-³x), is an exponential function. To differentiate it, we use the chain rule. The derivative of e^(-³x) is given by multiplying the derivative of the exponent (-³x) by the derivative of the exponential function e^x. The derivative of -³x is -3, and the derivative of e^x is e^x. Therefore, the derivative of e^(-³x) is -3e^(-³x).
The fifth term, ln(²+3)/5, involves the natural logarithm. To differentiate it, we use the chain rule. The derivative of ln(u) is given by multiplying the derivative of u by 1/u. In this case, the derivative of ln(²+3) is 1/(²+3) multiplied by the derivative of (²+3). The derivative of (²+3) is 2. Therefore, the derivative of ln(²+3) is 2/(²+3).
Now, let's put it all together and simplify the result:
h'(x) = 0 + e²-12 + 0 - (-3e^(-³x)) + (2/(²+3))/5.
Simplifying further:
h'(x) = e²-12 + 3e^(-³x) + 2/(5(²+3)).
Learn more about derivative at: brainly.com/question/29144258
#SPJ11
12 of the 28 dogs at the shelter are purebred what percent of the dogs are pure breed?HELP!
Answers
Answer:
57.142%
Step-by-step explanation:
28-12=16
16/28*100=57.142%
What innovation was made possible in part because of the Carterfone decision in 1968? Select one a. COBOL b. radiospectrum allocation c. the public Internet d. SMS
Answers
The innovation that was made possible in part because of the Carterfone decision in 1968 is the public Internet. The correct answer is option C
The Carterfone decision was a landmark ruling by the Federal Communications Commission (FCC) that allowed for the interconnection of third-party devices to the telephone network. Prior to this decision, telephone companies had a monopoly on the equipment that could be used on their networks, and customers were not allowed to attach their own devices.
This decision paved the way for the development of the public Internet by allowing for the interconnection of third-party devices to the telephone network, which enabled the creation of new technologies, such as modems. Without the Carterfone decision, the public Internet as we know it today may not have been possible.
Know more about innovation here:
https://brainly.com/question/30929075
#SPJ11
Find the matrix representing the total cost of material and transportation for steel, glass, and wood
Answers
The matrix representing the total cost of material and transportation for steel, glass, and wood is mathematically given as
\(\left[\right. Totat cost $=\left[\begin{array}{cccc}s & G & w \\ 11 & 6 & 39 & cost\ of\ material \\ 7 & 2 & 8 & cost\ on\ transportation.\end{array}\right]}\)
What is the matrix representing the total cost of material and transportation for steel, glass, and wood?Generally, the equation for is mathematically given as
(C) Giver matrices are
\(A=\left[\begin{array}{ccc}6 & 4 & 20 \\3 & 1 & 2\end{array}\right] \quad \& \quad B=\left[\begin{array}{ccc}5 & 2 & 19 \\4 & 1 & 6\end{array}\right]\)
Now to find the total cast A+B.
\($ total cost $=\left[\begin{array}{ccc}6 & 4 & 20 \\ 3 & 1 & 2\end{array}\right]+\left[\begin{array}{ccc}5 & 2 & 19 \\ 4 & 1 & 6\end{array}\right]$$=\left[\begin{array}{ccc}6+5 & 4+2 & 20+19 \\ 3+4 & 1+1 & 2+6\end{array}\right]$\)
In conclusion, The matrix represents the total cost of material and transportation
\($\left[\right.$ Totat cost $=\left[\begin{array}{cccc}s & G & w \\ 11 & 6 & 39 & cost\ of\ material \\ 7 & 2 & 8 & cost\ on\ transportation.\end{array}\right]$\)
Read more about the cost
https://brainly.com/question/15135554
#SPJ4
The complete Question is attached below

if a = 6, evaluate the following expression: 36/3a
Answers
Answer:
2
Step-by-step explanation:
1) substitute a=6 into 36/3a:
36/3×6
2) calculate: 36/3×6 ->2
what is the correct way to measure the zone of inhibition?
Answers
The correct way to measure the zone of inhibition is to place a known amount of an antimicrobial agent on a solid medium.
What is Area?Area is a quantity that measures the size of a two-dimensional surface or shape. It is expressed in square units such as square centimetres (cm2), square metres (m2) or square kilometres (km2). Area is used to describe the size of a garden, a house, a room, a city and much more. It can also be used to calculate the amount of material required for a project, such as paint, carpet or tiles. Knowing the area of a shape can help to calculate costs, and to make sure that enough materials are ordered.
The zone of inhibition is then measured as the area surrounding the antimicrobial agent where microbial growth has been inhibited. This area is typically measured in millimeters. To accurately measure the zone of inhibition, it is important to ensure that the size of the inoculum and the amount of antimicrobial agent used remain constant. Additionally, it is important to consider the type of organism being studied, as different organisms can have different levels of susceptibility to the antimicrobial agent. Finally, the medium used should be appropriate for the organism being studied, as different media can produce different results.
To know more about area click-
https://brainly.com/question/28012687
#SPJ1
HELP ILL MARK BRAINLIEST

Answers
Answer:
9c+5.9d−7.9
Step-by-step explanation:
hope this helps!
What is the domain and the range

Answers
Answer:
The Domain is X and Range is Y
Step-by-step explanation:
Top values are domain and bottom values are Range
Need help (no beginners)

Answers
Answer:
None of the above
Step-by-step explanation:
-5/2 is not equal to 5/2
5/2 - 39/8 = -19/8
if you calculate the two options you will see that none of them is equal to -19/8
The graph shows a system of equations: Draw a line labeled y equal s x plus 4 by joining the ordered pairs negative 4, 0 and 1, 5. Draw a line labeled 3 times y equals minus 2 x plus 2 by joining the ordered pairs negative 2, 2 and 4, negative 2. What is the solution to the system of equations?
Answers
The solution to the system of equations is (-2, 2).
Given that the graph shows a system of equations, we need to draw a line labeled y = x + 4 by joining the ordered pairs (-4, 0) and (1, 5). We also need to draw a line labeled 3y = -2x + 2 by joining the ordered pairs (-2, 2) and (4, -2).
Now, to find the solution to the system of equations, we need to identify the point where these two lines intersect.
This point will represent the solution to the system of equations. We can find this point by solving the two equations simultaneously.
Using the first equation, y = x + 4, we can substitute this value of y into the second equation, 3y = -2x + 2, to get:3(x + 4) = -2x + 2 Simplifying this equation, we get:3x + 12 = -2x + 2 5x = -10 x = -2Substituting this value of x back into the first equation, y = x + 4, we get:y = -2 + 4 y = 2
This is the point where the two lines intersect.
For more such questions on equations
https://brainly.com/question/22688504
#SPJ8
Ralph placed a classified ad to sell his used SUV for $18,500. After two weeks, he didn't sell the SUV, and the newspaper suggested lowering the price 5%. What would the new price be if Ralph reduced it according to the suggestion?
Answers
Answer:
17575
Step-by-step explanation:
18500*.05=925
18500-925=17575
17575 would be the new price if Ralph reduced it according to the suggestion.
What is multiplication?When you take a single number and multiply it by several, you are multiplying. There are a number of distinct indications of amplification that people utilize. The "x" sign represents the most typical, however other symbols like the "*" sign are also occasionally used.
The information that is present with respect to Ralph and the SUV is
Sell SUV at $18,500
Lowered the price by 5%
The reduction that is made in the price is
= 18500 * 5/ 100
= 18500 * 0.05
= 925
The new price of the SUV will be
= 18500 - 925
= 17575
The new price if Ralph reduced it by 5% will be 17575.
Learn more about multiplication, here:
https://brainly.com/question/5992872
#SPJ2
a large software company gives job applicants a test of programming ability and the mean for that test has been 160 in the past. twenty-five job applicants are randomly selected from one large university and they produce a mean score and standard deviation of 183 and 12, respectively. use a 0.05 level og significance to test the claim that this sample comes from a population with a mean score greater than 160. use the P-value method of testing hypotheses.
Answers
Using the P-value method of testing hypotheses with a significance level of 0.05, the sample provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
To test the claim that the mean score of job applicants from the university is greater than 160, we will perform a one-sample t-test using the P-value method. The null hypothesis (H0) assumes that the mean score is equal to 160, while the alternative hypothesis (Ha) assumes that the mean score is greater than 160.
First, we calculate the test statistic, which is the t-value. The formula for the t-value is:
t = (sample mean - hypothesized mean) / (sample standard deviation / sqrt(sample size))
Plugging in the given values, we have:
t = (183 - 160) / (12 / √(25))
= 23 / (12 / 5)
= 23 * (5 / 12)
≈ 9.58
Next, we find the P-value associated with the test statistic. The P-value represents the probability of obtaining a test statistic as extreme as the observed value, assuming the null hypothesis is true. Since the alternative hypothesis is one-sided (greater than 160), we calculate the P-value by finding the probability of the t-distribution with 24 degrees of freedom being greater than the calculated t-value.
Consulting statistical tables or using software, we find that the P-value is very small (less than 0.0001).
Since the P-value (less than 0.0001) is less than the significance level (0.05), we reject the null hypothesis. This provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
Learn more about P-value
brainly.com/question/30461126
#SPJ11
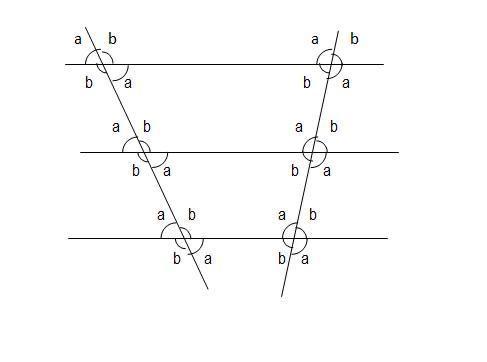
Notice that two line segments are formed on each transversal between the central parallel line and the outer parallel lines. Measure the lengths of the four line segments.
Answers
Answer:
Picture?
Step-by-step explanation:
Answer:
heres the picture
Step-by-step explanation:
7.) Thazzie solved 5 math problems while Zhaniyah finished all the remaining 8problems. What percent of the math problems was Thazzie able to solve?
Answers
ANSWER:
38.46%
STEP-BY-STEP EXPLANATION:
Given:
Problems solved by Thazzie: 5 problems
Problems solved by Zhaniyah: 8 problems
Which means that there are 13 problems in total.
Therefore, those 5 represent the following percent:
\(\begin{gathered} p=\frac{5}{13}\cdot100 \\ \\ p=38.46\% \end{gathered}\)Therefore, it represents 38.46% of the problems solved by Thazzie
I’ll give Brainliest (need ASAP)

Answers
Answer:
1.55
Step-by-step explanation:
you just change the fractions to decimals
. (strang 1.2.29) if ||~v|| = 5 and || ~w|| = 3, what are the smallest and largest possible values of: (a) ||~v − ~w|| (b) ~v · ~w
Answers
(a) The smallest possible value of ||~v − ~w|| is 2, which occurs when ~v and ~w are in the same direction. The largest possible value of ||~v − ~w|| is 8, which occurs when ~v and ~w are in opposite directions.
(b) The smallest possible value of ~v · ~w is -15, which occurs when ~v and ~w are in opposite directions. The largest possible value of ~v · ~w is 15, which occurs when ~v and ~w are in the same direction.
(a) The smallest possible value of ||~v − ~w|| occurs when ~v and ~w are in the same direction, so ||~v − ~w|| = ||~v|| - ||~w|| = 5 - 3 = 2. The largest possible value of ||~v − ~w|| occurs when ~v and ~w are in opposite directions, so ||~v − ~w|| = ||~v|| + ||~w|| = 5 + 3 = 8.
(b) The smallest possible value of ~v · ~w occurs when ~v and ~w are in opposite directions, so ~v · ~w = -||~v|| ||~w|| = -(5)(3) = -15. The largest possible value of ~v · ~w occurs when ~v and ~w are in the same direction, so ~v · ~w = ||~v|| ||~w|| = (5)(3) = 15.
To know more about same direction click on below link:
https://brainly.com/question/12002625#
#SPJ11
The time between busses on Stevens Creek Blvd is 10 minutes. Therefore the wait time of a passenger who arrives randomly at a bus stop is uniformly distributed between 0 and 16 minutes.
a. Find the probability that a person randomly arriving at the bus stop to wait for the bus has a wait time of at most 7 minutes.
b. Find the 80th percentile of wait times for this bus, for people who arrive randomly at the bus stop.
c. Find the mean and standard deviation
Answers
a. the probability that a person randomly arriving at the bus stop has a wait time of at most 7 minutes is 7/16. b. the 80th percentile of wait times for this bus is 12.8 minutes. c. the mean wait time is 8 minutes, and the standard deviation is approximately 4.62 minutes.
a. To find the probability that a person randomly arriving at the bus stop has a wait time of at most 7 minutes, we can calculate the cumulative probability of the uniform distribution.
Since the wait time is uniformly distributed between 0 and 16 minutes, the probability density function (PDF) is given by:
f(x) = 1/(b - a) = 1/(16 - 0) = 1/16
The cumulative distribution function (CDF) is the integral of the PDF from 0 to x:
F(x) = ∫[0, x] f(t) dt = ∫[0, x] (1/16) dt = (1/16) * t |[0, x] = x/16
To find the probability of a wait time of at most 7 minutes, we substitute x = 7 into the CDF:
P(X ≤ 7) = F(7) = 7/16
Therefore, the probability that a person randomly arriving at the bus stop has a wait time of at most 7 minutes is 7/16.
b. To find the 80th percentile of wait times for this bus, we need to determine the value x such that the cumulative probability up to x is 0.8. In other words, we need to find the value of x for which F(x) = 0.8.
Using the CDF derived earlier, we can solve the equation:
x/16 = 0.8
Multiplying both sides by 16, we get:
x = 0.8 * 16 = 12.8
Therefore, the 80th percentile of wait times for this bus is 12.8 minutes.
c. The mean and standard deviation of a uniform distribution can be calculated using the following formulas:
Mean (μ) = (a + b) / 2
Standard Deviation (σ) = (b - a) / √12
For the given uniform distribution with wait times ranging from 0 to 16 minutes:
Mean (μ) = (0 + 16) / 2 = 8 minutes
Standard Deviation (σ) = (16 - 0) / √12 ≈ 4.62 minutes
Therefore, the mean wait time is 8 minutes, and the standard deviation is approximately 4.62 minutes.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
Identify the highlighted part of circle O shown below
Central angle
Secant
Inscribed angle
Chord

Answers
Answer:
Chord
Step-by-step explanation:
Notice that the highlighted part is the line segment that joins the points J and E on the circle, which is known as a chord.
there are currently 63 million cars in a certain country, decreasing by 4.3 nnually. how many years will it take for this country to have 45 million cars? (round to the nearest year.)
Answers
It will take approximately 4 years for the country to have 45 million cars.
To find out how many years it will take for the country to have 45 million cars, set up an equation based on the given information.
Let's denote the number of years it will take as "t".
the number of cars is decreasing by 4.3 million annually. So, the equation becomes:
63 million - 4.3 million * t = 45 million
Simplifying the equation:
63 - 4.3t = 45
Now, solve for "t" by isolating it on one side of the equation. Let's subtract 63 from both sides:
-4.3t = 45 - 63
-4.3t = -18
Dividing both sides by -4.3 to solve for "t", we get:
t = (-18) / (-4.3)
t ≈ 4.186
Since, looking for the number of years, round to the nearest year. In this case, t ≈ 4 years.
Therefore, it will take approximately 4 years for the country to have 45 million cars.
Learn more about equation here:
https://brainly.com/question/10724260
#SPJ11
Answer the following questions and justify your answers. [Hint: Calculus may be helpful for some part(s).] a) [10 marks ] Show that en=Ω(n2). b) [10 marks] Show that n2+n+logn=θ(n2). c) [10 marks] Let f(x)=2x2+3x4+2x2 and g(x)=x2. Is f(x)=O(g(x)) ? Justify your answer. d) [10 marks] Let f(n) and g(n) be non-negative functions. Show that f(n)=Θ(g(n)) if and only if g(n)=θ(f(n)).
Answers
If g(n) = θ(f(n)), it means there exist positive constants c3, c4, and n0' such that for all n ≥ n0', c3(f(n)) ≤ g(n) ≤ c4(f(n)). By transitivity, we can conclude that c3c1(g(n)) ≤ f(n) ≤ c2c4(g(n)).
Therefore, f(n) = Θ(g(n)) if and only if g(n) = θ(f(n)).
a) To show that en = Ω(n^2), we need to find constants c and n0 such that for all n ≥ n0, en ≥ c(n^2).
Using the limit definition of Big Omega notation, we have to show that lim(n→∞) (en/n^2) ≥ c for some positive constant c.
Taking the natural logarithm of both sides, we get ln(en/n^2) = ln(e) = 1.
Since 1 is a positive constant, we can choose c = 1. Therefore, en = Ω(n^2).
b) To show that n^2 + n + log(n) = θ(n^2), we need to find constants c1, c2, and n0 such that for all n ≥ n0, c1(n^2) ≤ n^2 + n + log(n) ≤ c2(n^2).
By simplifying the expression, we have log(n) ≤ n.
Taking the natural logarithm of both sides, we get ln(log(n)) ≤ ln(n).
Since ln(n) grows faster than ln(log(n)), we can choose c1 = 1 and c2 = 2. Therefore, n^2 + n + log(n) = θ(n^2).
c) To determine if f(x) = O(g(x)), we need to find constants c and x0 such that for all x ≥ x0, f(x) ≤ c(g(x)).
By evaluating the functions, we have 2x^2 + 3x^4 + 2x^2 ≤ cx^2 for all x ≥ x0.
Simplifying, we get 5x^4 ≤ cx^2.
Since 5x^4 grows faster than cx^2, we can choose c = 5. Therefore, f(x) = O(g(x)).
d) To show that f(n) = Θ(g(n)) if and only if g(n) = θ(f(n)), we need to show that both f(n) = O(g(n)) and g(n) = O(f(n)).
If f(n) = Θ(g(n)), it means there exist positive constants c1, c2, and n0 such that for all n ≥ n0, c1(g(n)) ≤ f(n) ≤ c2(g(n)).
Similarly, if g(n) = θ(f(n)), it means there exist positive constants c3, c4, and n0' such that for all n ≥ n0', c3(f(n)) ≤ g(n) ≤ c4(f(n)).
By transitivity, we can conclude that c3c1(g(n)) ≤ f(n) ≤ c2c4(g(n)).
Therefore, f(n) = Θ(g(n)) if and only if g(n) = θ(f(n)).
to learn more about constants
https://brainly.com/question/31749950
#SPJ11
3. Karrie was late to work 14 times last year.
she worked 250 days last year, what perc
of the days was she late?
Answers
On solving the provided question, we can say that percentage of the days was she late = 14/250 * 100 = 5.6%
What is percentage?A percentage in mathematics is a figure or ratio that is stated as a fraction of 100. The abbreviations "pct.," "pct," and "pc" are also occasionally used. It is frequently denoted using the percent symbol "%," though. The amount of percentages has no dimensions. With a denominator of 100, percentages are basically fractions. To show that a number is a percentage, place a percent symbol (%) next to it. For instance, if you correctly answer 75 out of 100 questions on a test (75/100), you receive a 75%. To compute percentages, divide the amount by the total and multiply the result by 100. The percentage is calculated using the formula (value/total) x 100%.
Karrie was late to work = 14 times last year.
she worked = 250 days last year
percentage of the days was she late = 14/250 * 100 = 5.6%
To know more about percentage visit:
https://brainly.com/question/28269290
#SPJ1
