help solve please x^3-2x^2-2=0
Answers
Answer:
x=2.35930...
i hope this is the answer
Related Questions
solve for x
HELP PLEASE

Answers
A reporter for a local television station visits the city's new upscale shopping mall the day before Christmas to interview shoppers. He questions the first 25 shoppers he meets outside one of department stores at the mall. He asks them whether their overall feelings about Christmas shopping are positive, neutral, or negative. re Select the reason(s) why it may be risky to act as if the first 25 shoppers at this particular location are an SRS of all shoppers in the city. Shoppers at the mall the day before Christmas does not guarantee every shopper in the population has an equal chance to be in the sample Surveying shoppers the day before Christmas is a convenience sample, so it is a simple random sample Surveying shoppers at the mall the day after Christmas may not be a good represenation of all shoppers in the city. Having the reporter ask questions is not a double-blind study.
Answers
The correct option is A shopping center surveys conducted the day before Christmas do not guarantee that every shopper in the population will be included in the sample.
Given that,
The day before Christmas, a reporter from a nearby television station goes to the city's brand-new, upmarket retail center to speak with customers. The first 25 customers he encounter outside one of the mall's department stores are questioned. He inquires as to whether they have a positive, neutral, or negative overall opinion of Christmas shopping.
We have to select the correct option why it might be dangerous to assume that the first 25 customers at this store are representative of all customers in the city.
We know that,
A non-probability sampling technique called convenience sampling includes taking a sample from the nearest area of the population. It is a convenience sample because the reporter in the scenario asked the first 25 people he saw outside one of the department stores at the mall. Each candidate does not have an equal chance of being included in the convenience sample.
The right response is option (A): Shopping center surveys conducted the day before Christmas do not guarantee that every shopper in the population will be included in the sample.
To learn more about christmas visit: https://brainly.com/question/29626426
#SPJ4
The depth of a river is being measured. From the shore line the river was 25 meters deep. 1 mile out the river was 35 meters deep. 2 miles out the river was 45 meters deep. If the depth continues in this sequence, what will the equation be? Is it linear or exponential? Is this situation discrete or continuous?
Answers
The equation will be linear because the change in depth is constant for each unit of distance from the shoreline.
What is the Linear equation?A linear equation is defined as an equation in which the highest power of the variable is always one.
From the information provided, we can see that the depth of the river increases by 10 meters for every 1 mile of distance from the shoreline.
Therefore, we can assume that the equation that relates the depth (D) of the river to the distance (X) from the shoreline is:
D = 25 + 10X
This equation is linear since the change in depth is constant for each unit of distance from the shoreline.
However, we should note that the situation described is actually discrete rather than continuous. The depths are only given for specific distances (every 1 mile), and we do not have any information about the depths between those specific distances.
Therefore, we cannot assume that the depth of the river changes continuously as the distance from the shoreline increases. Instead, the depth changes in discrete steps at each mile.
Learn more about the Linear equations here:
https://brainly.com/question/13738061
#SPJ1
find the value of y+20 when y=8
Answers
The value of the expression; y + 20 when y = 8 as required in the task content is; 28.
What is the result of the evaluation of; y + 20 when y = 8?It follows from the task content that the value of the expression; y + 20 is to be determined given that the variable, y is equal to 8.
Since the given expression is; y + 20.
However, the given value of y is such that; y = 8.
Therefore, by the substitution property of equality; the resulting expression is;
8 + 20
= 28.
Ultimately, the value of the expression; y + 20 when y = 8 is; 28.
Read more on expressions;
https://brainly.com/question/28912738
#SPJ1
Y=-2/3x+4 Solve for x
Answers
Answer:
answer should be x = -3y/2 + 6
hope it helps :D
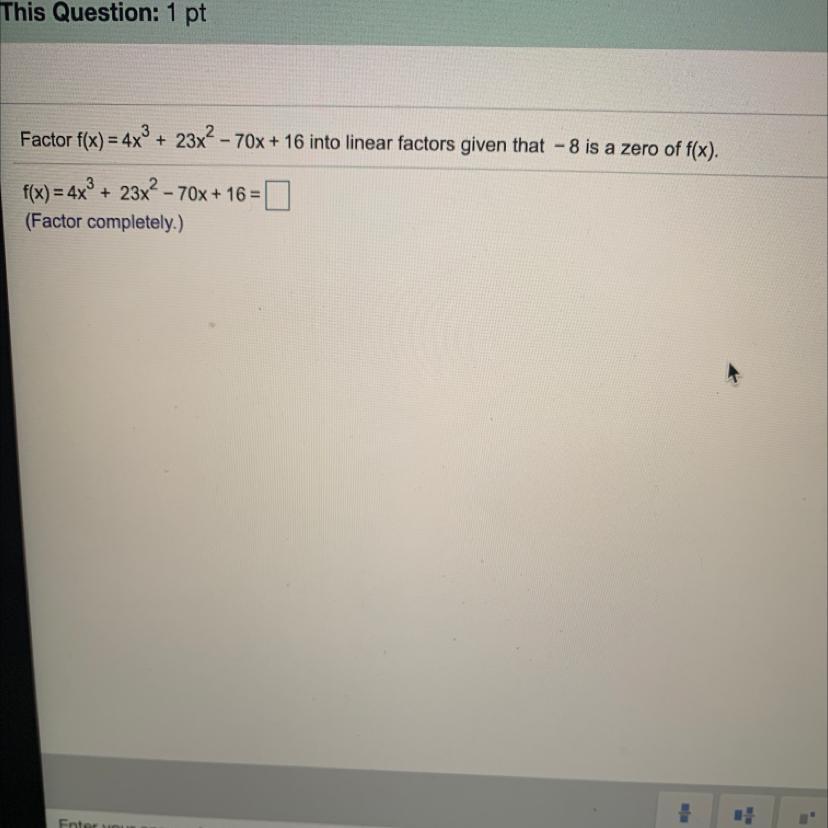
help:) Factor f(x) = 4x^3+ 23x^2- 70x + 16 into linear factors given that - 8 is a zero of f(x).
Answers
Answer:
(x + 8)(x - 2)(4x - 1)
Step-by-step explanation:
Given that x = - 8 is a zero then (x + 8) is a factor
Divide f(x) by (x + 8) using Synthetic division
- 8 | 4 23 - 70 16
↓ - 32 72 - 16
---------------------------------
4 - 9 2 0
Quotient = 4x² - 9x + 2 = (x - 2)(4x - 1)
Thus
f(x) = (x + 8)(x - 2)(4x - 1)
An amusement park has 15 roller coasters. In how many ways can you choose 10 of the roller coasters to ride during your visit to the park? *
Answers
Answer:
3003 ways
Step-by-step explanation:
We are in a combination or permutation exercise, the difference between them is if the order matters (permutations) or does not matter (combinations),
in this case the order does not matter, since they only ask us for the ways to choose 10 of 15 roller coasters, therefore it would be a combination:
nCr = n! / (r! * (n-r)!
we know that n = 15 and r = 10, we replace:
15C10 = 15! / (10! * (15-10)!
15C10 = 3003
In other words, there are 3003 ways to choose 10 of the 15.
Write the equation for the relationship 19
Answers
Answer:
Did you mess up the question? This doesn't make any sense. If you post a new question I can help! Otherwise uhhh x=9*2 ???
NO LINKS!! Please help me with this problem 2dd

Answers
Answer:
\(\begin{array}{|c|c|} \cline{1-2}\text{n} & \text{A}\\\cline{1-2}1 & 4376.10\\\cline{1-2}2 & 4442.10\\\cline{1-2}4 & 4476.86\\\cline{1-2}12 & 4500.73\\\cline{1-2}365 & 4512.49\\\cline{1-2}\text{Continuous} & 4512.89\\\cline{1-2}\end{array}\)
The values in the second column represent dollar figures.
There's no need to type in the dollar symbol into the boxes since each dollar sign is taken care of by your teacher.
I would avoid typing commas into the boxes since it might cause the computer to mark the answer wrong.
==================================================
Work Shown:
P = 2100 dollar depositr = 0.085 = annual interest rate in decimal formt = 9 yearsThese values will be used in every section, including the final section at the bottom. For the first five sections, the only input that changes is the value of n.
--------------------
n = 1 = annual or 1 time a year compounding
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/1)^(1*9)
A = 2100*(1.085)^9
A = 2100*2.08385570683634
A = 4376.09698435631
A = 4376.10
Therefore, if the money is compounded 1 time per year (aka annually), then you'll have $4,376.10 in the account after the 9 year period. The interest rate must stay at 8.5%; also you cannot deposit nor withdraw money from this account.
We'll repeat these similar steps for the other sections, with the exception of the last section that uses a different formula.
Your steps or work shown to your teacher doesn't need to be as verbose as I have written above. You can have this shortened version like this perhaps:
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/1)^(1*9)
A = 4376.09698435631
A = 4376.10
I'm choosing to be a bit "wordy" in terms of steps to show how the order of operations PEMDAS is playing out. Use of a spreadsheet is recommended to quickly compute these values, as well as organize the items in a handy table (as shown above).
--------------------
n = 2 = semiannual compounding, aka every 6 months
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/2)^(2*9)
A = 2100*(1+0.0425)^(18)
A = 2100*(1.0425)^18
A = 2100*2.11528624641441
A = 4442.10111747027
A = 4442.10
--------------------
n = 4 = quarterly compounding
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/4)^(4*9)
A = 2100*(1+0.02125)^(36)
A = 2100*(1.02125)^(36)
A = 2100*2.13183949332905
A = 4476.86293599101
A = 4476.86
--------------------
n = 12 = monthly compounding
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/12)^(12*9)
A = 2100*(1+0.0070833333)^(108)
A = 2100*(1.0070833333)^(108)
A = 2100*2.14320709156311
A = 4500.73489228253
A = 4500.73
---------------------
n = 365 = daily compounding, ignoring leap years
A = P*(1+r/n)^(n*t)
A = 2100*(1+0.085/365)^(365*9)
A = 2100*(1+0.000232876712328767)^(3285)
A = 2100*(1.00023287671233)^(3285)
A = 2100*2.14880299048115
A = 4512.48628001041
A = 4512.49
---------------------
The continuous case:
As n gets larger, it appears that the value of A is approaching around $4512.49 or so. Perhaps the amount may be slightly larger.
To account for n going to infinity, we use the continuously compounded interest formula
A = P*e^(r*t)
to plug in
P = 2100r = 0.085t = 9The 'e' refers to the special constant e = 2.718...
Let your calculator handle this value. There should be a button with the single letter "e" on it.
So,
A = P*e^(r*t)
A = 2100*e^(0.085*9)
A = 4512.88818677718
A = 4512.89
Each result is shown in the table at the top of the solution.
Don't forget to round to the nearest hundredth.
Answer:
\(\begin{array}{|c|c|}\cline{1-2} \vphantom{\dfrac12} n& A\\\cline{1-2} \vphantom{\dfrac12} \sf 1& \$ \;\boxed{\sf 4376.10}\\\cline{1-2} \vphantom{\dfrac12} \sf 2& \$ \;\boxed{\sf 4442.10}\\\cline{1-2} \vphantom{\dfrac12} \sf 4& \$ \;\boxed{\sf 4476.86}\\\cline{1-2} \vphantom{\dfrac12} \sf 12& \$ \;\boxed{\sf 4500.73}\\\cline{1-2} \vphantom{\dfrac12} \sf 365& \$ \;\boxed{\sf 4512.49}\\\cline{1-2} \vphantom{\dfrac12} \sf Continuous & \$ \;\boxed{\sf 4512.89}\\\cline{1-2} \end{array}\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+\frac{r}{n}\right)^{nt}$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given:
P = $2100r = 8.5% = 0.085t = 9 yearsSubstitute the given values into the formula to create a formula for n number of years:
\(\implies A=2100\left(1+\dfrac{0.085}{n}\right)^{9n}\)
To complete the first five rows of the table, substitute each value of n into the found formula.
\(\begin{aligned}n=1 \implies A& =2100\left(1+\dfrac{0.085}{1}\right)^{9 \cdot 1}\\A& =2100\left(1.085\right)^{9}\\A& =4376.10\end{aligned}\)
\(\begin{aligned}n=2 \implies A& =2100\left(1+\dfrac{0.085}{2}\right)^{9 \cdot 2}\\A& =2100\left(1.0425\right)^{18}\\A& =4442.10\end{aligned}\)
\(\begin{aligned}n=4 \implies A& =2100\left(1+\dfrac{0.085}{4}\right)^{9 \cdot 4}\\A& =2100\left(1.02125\right)^{36}\\A& =4476.86\\\end{aligned}\)
\(\begin{aligned}n=12 \implies A& =2100\left(1+\dfrac{0.085}{12}\right)^{9 \cdot 12}\\A& =2100\left(1.00708333...\right)^{108}\\A& =4500.73\end{aligned}\)
\(\begin{aligned}n=365 \implies A& =2100\left(1+\dfrac{0.085}{365}\right)^{9 \cdot 365}\\A& =2100\left(1.00023287...\right)^{3285}\\A& =4512.49\end{aligned}\)
\(\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Formula}\\\\$ A=Pe^{rt}$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}\)
Substitute the given values into the formula to find the balance of the account when the interest is continuously compounding:
\(\implies A=2100 \cdot e^{0.085 \cdot 9}\)
\(\implies A=2100 \cdot e^{0.765}\)
\(\implies A=4512.89\)
Completed table:
\(\begin{array}{|c|c|}\cline{1-2} \vphantom{\dfrac12} n& A\\\cline{1-2} \vphantom{\dfrac12} \sf 1& \$ \;\boxed{\sf 4376.10}\\\cline{1-2} \vphantom{\dfrac12} \sf 2& \$ \;\boxed{\sf 4442.10}\\\cline{1-2} \vphantom{\dfrac12} \sf 4& \$ \;\boxed{\sf 4476.86}\\\cline{1-2} \vphantom{\dfrac12} \sf 12& \$ \;\boxed{\sf 4500.73}\\\cline{1-2} \vphantom{\dfrac12} \sf 365& \$ \;\boxed{\sf 4512.49}\\\cline{1-2} \vphantom{\dfrac12} \sf Continuous & \$ \;\boxed{\sf 4512.89}\\\cline{1-2} \end{array}\)
A road has a speed limit sign at the beginning that is noticed by 84 % of people. 95 % of people who didn't notice the sign speed on the road. Of those who notice the sign, 75 % follow the speed limit.
How many percent of people speeding on this road noticed the sign? In other words, how many people on this road speed on purpose. Give your answer in percentage.
Answers
The percentage is the indicating hundredth thus the percentage of people speeding on this road who noticed the sign would be 84% - 75% = 9%.
What is the percentage?The percentage is defined as a given amount in every hundred. It is a fraction with 100 as the denominator percentage is represented by the one symbol %.
As per the given,
Percentage of people who notice the speed limit = 84%
The percentage of people who notice the sign and follow the speed limit is 75%.
Therefore, 84% - 75% = 9% are the percentage speeding and noticed.
Hence "The percentage is the indicating hundredth thus the percentage of people speeding on this road who noticed the sign would be 84% - 75% = 9%".
For more about the percentage,
brainly.com/question/13450942
#SPJ1
Which of the following is true about the linear function 4x+2y=12
1.it has a slope of -2 and a y intercept of 6
2. It has a slope of -2 and a y intercept of 12
3 it has a slope of -1/2 and a y intercept of 6
4 it has a slope of -4 and a y intercept of 12
Answers
Answer:
i believe is 4
Step-by-step explanation:
If you 2y=-4x+12
need to get the Y by it self
Determine the amplitude of function

Answers
The amplitudes of functions are a) 8 and b) 6.
Given are the functions we need to determine the amplitude of function,
a) y = 8 Sin (x/2) + 3
b) y = 6 Cos x + 2
So,
To determine the amplitude of a trigonometric function, you can follow these steps:
For a sine function of the form y = A×sin(Bx + C) + D:
The amplitude is equal to the absolute value of the coefficient A.
For a cosine function of the form y = A×cos(Bx + C) + D:
The amplitude is equal to the absolute value of the coefficient A.
Let's apply these steps to the given functions:
a) y = 8×sin(x/2) + 3
The coefficient of sin in this function is 8, so the amplitude is |8| = 8.
Therefore, the amplitude of function a) is 8.
b) y = 6×cos(x) + 2
The coefficient of cos in this function is 6, so the amplitude is |6| = 6.
Therefore, the amplitude of function b) is 6.
Hence the amplitudes of functions are a) 8 and b) 6.
Learn more about amplitude click;
https://brainly.com/question/9525052
#SPJ1
A local catering company ordered 15 pounds of chicken, 21 pounds of beef, and 7 pounds of lobster. The cost of the chicken was $2 per pound, the cost of the beef was $4 per pound, and the cost of the lobster was $12 per pound. What was the total cost of the order?
Answers
the total price of the catering company's order was $198.
To discover the total value of the order, we need to multiply the kilos of every type of meat via its respective cost in keeping with pound and then add those products together.
For the chook:
15 pounds x $2 per pound = $30
For the beef:
21 kilos x $4 per pound = $84
For the lobster:
7 pounds x $12 per pound = $84
Now, we add up the costs of each form of meat to find the total cost of the order:
$30 + $84 + $84 = $198
Consequently, the whole price of the catering company's order was $198.
Learn more about multiplication:-
https://brainly.com/question/29793687
#SPJ1
Please help fast easy points!

Answers
The probabilities and the odds are P(E) = 4/9, P(E) = 1/8 and o(E) = 1 : 7
How to determine the probabilitiesProbability P(E)
From the question, we have the following notation that can be used in our computation:
Odds, o(E) = 4 : 5
Using the above as a guide, we have the following probability equation
P(E) = 4/(4 + 5)
Evaluate
P(E) = 4/9
Probability P(E)
Here, we have
Odds, o(E) = 7 : 4
Using the above as a guide, we have the following probability equation
P(E) = 7/(7 + 4)
Evaluate
P(E) = 7/11
Odds (E)
Here, we have
P(E) = 1/8
Using the above as a guide, we have the following probability equation
o(E) = P(E) : 1 - P(E)
So, we have
o(E) = 1/8 : 7/8
Evaluate
o(E) = 1 : 7
Read more about probability at
https://brainly.com/question/251701
#SPJ1
f(x)=x^2+6x+7
f(x+h)=?
f(x+h)-f(x)=?
f(x+h)-f(x)/h=?
Answers
The values are;
f (x + h) = x² + 2xh + h² + 6x + 6h + 7
f (x + h) - f (x) = h² + 2xh + 6h
f (x + h) - f (x) / h = h + 2x + 6
What is substitution method?
Find the value of any one of the variables from one equation in terms of the other variable is called the substitution method.
Given that;
The value of the function is;
f (x) = x² + 6x + 7
Now, Find the given values of f (x + h) , f (x + h) - f (x) and f (x + h) - f (x) / h by substitution method.
The value of the function is;
f (x) = x² + 6x + 7
Substitute x = x + h;
The value of the function is;
f (x + h) = (x + h)² + 6(x + h) + 7
= x² + 2xh + h² + 6x + 6h + 7
Thus, The value of f (x + h) = x² + 2xh + h² + 6x + 6h + 7.
Now,
f (x + h) - f (x) = (x² + 2xh + h² + 6x + 6h + 7) - (x² + 6x + 7)
= x² + 2xh + h² + 6x + 6h + 7 - x² - 6x - 7
= h² + 2xh + 6h
Thus, The value of f (x + h) - f (x) = h² + 2xh + 6h.
Now,
f (x + h) - f (x) / h = h² + 2xh + 6h / h
= h (h + 2x + 6) / h
= h + 2x + 6
Thus, The value of f (x + h) - f (x) / h = h + 2x + 6.
Therefore, The values are;
f (x + h) = x² + 2xh + h² + 6x + 6h + 7
f (x + h) - f (x) = h² + 2xh + 6h
f (x + h) - f (x) / h = h + 2x + 6
Learn more about the substitution method visit:
https://brainly.com/question/19256999
#SPJ1
Enter your answer as a proper fraction, or mixed number.

Answers
Answer:
3/14
Step-by-step explanation:
Answer:
3/14
Step-by-step explanation:
1.
What is the common difference of the sequence 4, 11, 18, 25, 32?
9
7
8
14
Answers
Answer: 7
Step-by-step explanation: its correct, trust me
What is 23.58 in word form
Answers
The equilateral triangle shown has a perimeter of 30 inches and a height of a inches.
What is the value of a?
O 5 in
O 5√3 in
O10 in
•10√3 in
Answers
The height of the equilateral triangle is a = 5√3 inches
Given data ,
Since the triangle is equilateral, all sides are of equal length.
Let's call the length of one side x.
Therefore, the perimeter of the triangle is 3x, which is given to be 30 inches.
On simplifying , we get
3x = 30
x = 10
Now, we know that the height of an equilateral triangle is given by the formula:
height = √3/2 x
Substituting the value of x, we get:
height = √3/2 x 10
height = 5√3 inches
Hence , the height of triangle is 5√3 inches
To learn more about equilateral triangle click :
https://brainly.com/question/17824549
#SPJ1
Solve for x in the diagram below

Answers
Answer:
X=6
Step-by-step explanation:
5x+(x+54)=90
6x+54=90
6x=36
X=6
Can somebody please help me with question 2? Thanks! :)

Answers
Answer:72 bracelets
Step-by-step explanation:
24*3
72 bracelets
If she can make 4 bracelets with 12 beads, you divide to get three. Three times 24 is 72 bracelets
What is the quotient?
(6 * 108) = (1.5 * 10-4)
4 x 1012
4 x 104
4 x 10-32
410-2
Answers
Answer:
(A)\(4X10^{12}\)
Step-by-step explanation:
Given the quotient:
\(\dfrac{6*10^8}{1.5*10^{-4}}\)
To evaluate, we first separate the given expression as follows.
\(=\dfrac{6}{1.5}X\dfrac{10^8}{10^{-4}}\)
Next, we apply the division law of indices to the powers of 10.
Division Law of Indices: \(\frac{a^x}{a^y}=a^{x-y}\)
\(=4X10^{8-(-4)}\\=4X10^{8+4}\\=4X10^{12}\)
Therefore, our quotient is \(4X10^{12}\).
The correct answer is A.
help me please ill give brainlest

Answers
Answer:
D is the answer I think......
Please help me with #1Please help me on my hw

Answers
The given expression is,
\((2x^2)^3\)According to the law of exponents,
\(\begin{gathered} (xy)^m=x^my^m\text{ ---(a)} \\ (x^m)^n=x^{mn}\text{ ---(b)} \end{gathered}\)Applying the law of exponents to the given expression,
\(\begin{gathered} (2x^2)^3=2^3(x^2)^3\text{ (using law (a))} \\ =8x^{2\times3}\text{ (using law (b))} \\ =8x^6 \end{gathered}\)Therefore, the correct expression is
\((2x^2)^3=8x^6\)
A Car moves 45km in 45 min.What
is it speed in kilometres per hour
Answers
Hello !
45min = 3/4h = 0,75h
\(\frac{45km}{0,75h} \\\\= \frac{45km*\frac{1}{0,75} }{0,75h*\frac{1}{0,75} } \\\\= \frac{60km}{1h}\)
s = 60km/h
\(s=\dfrac{d}{t}\\\\d=45\text{ km}\\t=45\text{ min}=0.75\text{ h}\\\\s=\dfrac{45\text{ km}}{0.75\text{ h}}=60\dfrac{\text{km}}{\text{h}}\)
Approximate the root by using a linearization centered at an approximate nearby number
√101
Answers
Linearization is the idea in calculus where if you zoom in really close onto a section of the graph, the curve and the tangent line will be extremely similar to each other.
We can use this idea and approximate nearby values to the tangent line.
The parent graph of a square root function is \(f(x)=\sqrt{x}\).
There are two methods in which we can calculate the approximate value of \(\sqrt{101}\) by using linearization techniques.
Method 1:Write equation of tangent line.Find the value of y at x = 101.Let's use the nearest perfect square to \(\sqrt{101}\), which is \(\sqrt{100}\). When drawing the graph of the square root function, we use the point (100, 10) because where x = 100, y = 10 on a square root function.
Now, we have a point that the tangent line passes through, and we want to find the slope.
We can do so by taking the derivative of \(f(x) =\sqrt{x}\).
\(f'(x)=x^\frac{1}{2}\) \(f'(x)=\frac{1}{2} x^-^\frac{1}{2}\) \(f'(x)=\frac{1}{2x^\frac{1}{2} }\) \(}f'(x)=\frac{1}{2\sqrt{x} }\)Plug in x = 100 to find the slope of the tangent line here.
\(f'(100)=\frac{1}{2\sqrt{100} }\) \(f'(100)=\frac{1}{2(10)}=\frac{1}{20}\)The slope of the tangent line at x = 100 is 1/20. Now, we can use the point and the slope of the tangent line to determine the equation for the tangent line.
(100, 10), m = 1/20
Point-slope equation:
\(y-y_1=m(x-x_1)\) \(y-(10)=\frac{1}{20}(x-(100))\) \(y=\frac{1}{20}x-5+10\) \(y=\frac{1}{20}x+5\)To find the value of y at x = 101, plug this into the tangent line equation.
\(y=\frac{1}{20}(101)+5\) \(y=\frac{101}{20}+5\) \(y=\frac{101}{20} +\frac{100}{20} = \frac{201}{20}\)201/20 is equal to 10.05. Let's estimate the error of this calculation to the actual value of \(\sqrt{101}\), inputted into a calculator.
We get \(\sqrt{101}=10.04987562\), which is extremely close to 10.05. Our estimate using linearization only has an error of 0.00012.
Method 2:You may have noticed that the first method uses little calculus, apart from taking the derivative of f(x).
The more "calculus-y" method involves finding the change in y in terms of the change of x.
We know that dy/dx is the the change in y due to a change in x, so we can use this to find the change in y when x = 101.
\(\frac{dy}{dx} =\frac{1}{2\sqrt{x} }\)Solve for dy by mutliplying dx to both sides of the equation.
\(dy=\frac{1}{2\sqrt{x} } \cdot dx\)The change in x is 1, because 101 - 100 = 1.
We want to find the change in y when x = 100, and has a change of 1. Therefore, we have:
\(dx=1\) \(x=100\)Plug these values into the equation \(dy=\frac{1}{2\sqrt{x} } \cdot dx\) and solve for dy.
\(dy=\frac{1}{2\sqrt{200} } \cdot 1\) \(dy=\frac{1}{2(10)}\) \(dy=\frac{1}{20}\)The change in y when x = 100 with a change of 1 is 1/20. We know when x = 100 the y-value is 10. Therefore, when x = 101, the change in y is 1/20, so y = \(10\frac{1}{20} = \frac{201}{20} = 10.05\).
You can see that we get the same answer with either method.
Candice scored 74 on an exam that had a mean of 66 and a standard deviation of 4. Erin scored 58 on an exam with a mean of 42 and a standard deviation of 7. Who scored better?
Answers
Answer:
Erin
Step-by-step explanation:
Z score formula:
z = (x-μ)/σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation.
For Candice:
Z score = 74 -66/4
Z score = 2
For Erin
Z score = 58 - 42/7
Z score = 2.28571
Erin z score is larger hence, he did better
22% of high school students in the United Kingdom say that Dobby is their favoite character in the Harry Potter books. Let's assume this is the parameter value for the entire population of high school students in the U.K. You take a sample of 150 high school students and record the porportion, (p-hat) of individuals in your sample who say Dobby is their favorite character. a) What are the mean and Standard deviation of the sampling distribution of p-hat
Answers
Answer:
The mean of the sampling distribution is 0.22 and the standard deviation is 0.0338.
Step-by-step explanation:
Central Limit Theorem:
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
In this question, we have that:
\(p = 0.22, n = 150\)
a) What are the mean and Standard deviation of the sampling distribution of p-hat
By the Central Limit Theorem,
Mean:
\(\mu = p = 0.22\)
Standard deviation:
\(s = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0.22*0.78}{150}} = 0.0338\)
The mean of the sampling distribution is 0.22 and the standard deviation is 0.0338.
Frank's father came home from San Francisco by airplane. He had to wait 1 hour and 45 minutes at the airport in San Francisco. Then Frank's
father had to wait another 35 minutes while the plane was in Portland.
How long did Frank's father spend waiting?
Answers
Answer:
2 hrs and 20 minutes
Step-by-step explanation:
45 + 35 = 80
what is the square root of 4/25
Answers
Answer:
square roots of 25 =5
Step-by-step explanation:
5×5= 25