Answers
Answer:
Your answer is A.
Step-by-step explanation:
Looking at the graphing two-equation: y = x^3 -3 and y = x^2+6 are up there, it can help us determine the limit of domain.
The dot is the x<=2 for equation y=x^3-3.
The circle is x>2 for equation y=x^2+6
Related Questions
) Quantifier negation.
Form the negation of the following statements. Then apply De Morgan’s law and/or conditional law, when
applicable. Negation should appear only within predicates, i.e., no negation should be outside a quantifier
or an expression involving logical connectives. Show all steps.
a) ∀x (P(x) ∧ R(x))
b) ∀y∃z(¬P(y) → Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Answers
The negations of the given statements with the application of De Morgan's law and/or conditional law.
a) ∃x (¬P(x) ∨ ¬R(x))
De Morgan's law:
∃y ∀z(¬P(y) ∧ ¬Q(z))
b) ∃y ∀z(¬P(y) ∧ ¬Q(z))
The double negation:
∃y ¬∃z(P(y) ∨ Q(z))
c) ¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
The conditional law:
¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
Let's form the negation of the given statements and apply De Morgan's law and/or conditional law, when applicable:
a) ∀x (P(x) ∧ R(x))
The negation of this statement is:
∃x ¬(P(x) ∧ R(x))
Now let's apply De Morgan's law:
∃x (¬P(x) ∨ ¬R(x))
b) ∀y∃z(¬P(y) → Q(z))
The negation of this statement is:
∃y ¬∃z(¬P(y) → Q(z))
Using the conditional law, we can rewrite the negation as:
∃y ¬∃z(¬¬P(y) ∨ Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
The negation of this statement is:
¬∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Using the conditional law, we can rewrite the negation as:
¬∃x (P(x) ∨ (∀z (R(z) ∨ ¬Q(z))))
Applying De Morgan's law:
¬∃x (P(x) ∨ (∀z ¬(¬R(z) ∧ Q(z))))
Simplifying the double negation:
¬∃x (P(x) ∨ (∀z ¬(R(z) ∧ Q(z))))
Using De Morgan's law again:
¬∃x (P(x) ∨ (∀z (¬R(z) ∨ ¬Q(z))))
For similar questions on De Morgan's law
https://brainly.com/question/28735989
#SPJ8
using the numbers 1-9, at most one time each, fill the blanks to make this equation true. find one solution for this equation.( ) = 81
Answers
The solution for this equation is (3¹)⁴=81.
The power of a number defines how many times to use the number in multiplication, Powers are also called Exponents or Indices.
If the power is positive, multiply the number by itself that many times. If the power is negative, multiply the number's reciprocal by itself that many times. If the power is zero, the result will always be 1.
For example, 8^2 could be called “8 to the power 2” “8 to the second power”, or simply “8 squared”.
A number, X, to the power of 2 is also referred to as X squared.
X is called the base number.
To know more about the Powers of a number:
https://brainly.com/question/25263760
#SPJ4
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = In x
Y = 1
Y = 2
X = 0
About the Y axis
Answers
Work attached in image. Since the solid is being rotated about the y-axis, you would need to solve y=lnx in terms of x. The rest of the process is showed in the image.

Finding Missing Angles in a Polygon

Answers
The value of x° is 133°.
Given,
Pentagon with angles 107° , 120° , 90° , 90° , x° .
A pentagon is formed by combining three triangles and thus have total of interior angles to be 540°.
Now, to calculate the value of x:
Sum of all interior angles of pentagon = 540°
Put the values of all the angles given in the figure,
120° + 107° + 90° + 90° + x° = 540°
407° + x = 540°
x = 133°
Hence the missing angle is of 133° .
Know more about Polygons,
https://brainly.com/question/17756657
#SPJ1
What is the volume of this rectangular prism?
A)40 cu in
B)120 cu in
C)22cu in
D)84 cu in
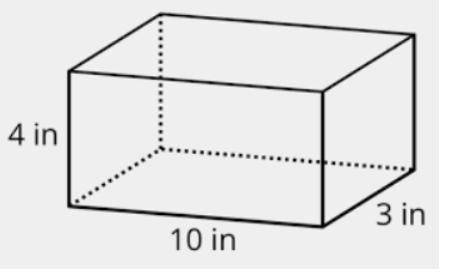
Answers
Answer: B (120 in^3)
Step-by-step explanation: W * L *H = V
Length * Width * Height = Volume
You can multiply the LWH in any order.
Height = 4
Length = 10
Width = 3
Remember, anything multiplied by ten is just the product (answer) with a zero added to the end. Example: 4 * 3 = 12; 12 * 10 = 120
Another Example: 15 * 2 = 30; 30 * 10 = 300
4 * 10 = 40
40 * 3 = 120
Therefore, 120 is your answer.
Hope this helps!
Answer:
The answer to your problem is, 120 cu in
Step-by-step explanation:
In order to find the volume of the cube there is only one thing that you need to do which is pretty simple just follow these steps:
Multiply, l * w * h ( * = multiply )
By following the formula up above you can find the volume of a rectagular prism which is:
4 x 10 = 40
3 x 40 = 120.
Thus the answer to you problem is, 120 cu in
Complete the equation of the line through (6,-6 ) and (8, 8) Use exact numbers. y=
Answers
Answer:
\( m =\frac{y_2 -y_1}{x_2 -x_1}\)
And replacing we got:
\( m=\frac{8-(-6)}{8-6}= 7\)
And now we can use one of the points and we can find the intercept b like this:
\( 8 = 7*8 +b\)
And solving for b we got:
\( b = 8 -56 = -48\)
And the line would be:
\( y = 7x -48\)
Step-by-step explanation:
For this case we have two points given :
(x1=6,y1=-6) and (x2=8,y2=8)
We can find the line equation given by:
\( y = mx+b\)
The slope would be:
\( m =\frac{y_2 -y_1}{x_2 -x_1}\)
And replacing we got:
\( m=\frac{8-(-6)}{8-6}= 7\)
And now we can use one of the points and we can find the intercept b like this:
\( 8 = 7*8 +b\)
And solving for b we got:
\( b = 8 -56 = -48\)
And the line would be:
\( y = 7x -48\)
An isosceles triangle whose sides are 5cm, 5cm and 6cm is inscribed in a circle. Find the radius of the circle.
Answers
Answer:
To find the radius of the circle inscribed in an isosceles triangle, we can use the following formula:
r = (a/2) * cot(π/n)
where r is the radius of the inscribed circle, a is the length of one of the equal sides of the isosceles triangle, and n is the number of sides of the polygon inscribed in the circle.
In this case, we have an isosceles triangle with two sides of 5cm and one side of 6cm. Since the triangle is isosceles, the angle opposite the 6cm side is bisected by the altitude and therefore, the two smaller angles are congruent. Let x be the measure of one of these angles. Using the Law of Cosines, we can solve for x:
6^2 = 5^2 + 5^2 - 2(5)(5)cos(x)
36 = 50 - 50cos(x)
cos(x) = (50 - 36)/50
cos(x) = 0.28
x = cos^-1(0.28) ≈ 73.7°
Since the isosceles triangle has two equal sides of length 5cm, we can divide the triangle into two congruent right triangles by drawing an altitude from the vertex opposite the 6cm side to the midpoint of the 6cm side. The length of this altitude can be found using the Pythagorean theorem:
(5/2)^2 + h^2 = 5^2
25/4 + h^2 = 25
h^2 = 75/4
h = sqrt(75)/2 = (5/2)sqrt(3)
Now we can find the radius of the inscribed circle using the formula:
r = (a/2) * cot(π/n)
where a = 5cm and n = 3 (since the circle is inscribed in a triangle, which is a 3-sided polygon). We can also use the fact that the distance from the center of the circle to the midpoint of each side of the triangle is equal to the radius of the circle. Therefore, the radius of the circle is equal to the altitude of the triangle from the vertex opposite the 6cm side:
r = (5/2) * cot(π/3) = (5/2) * sqrt(3) ≈ 2.89 cm
Therefore, the radius of the circle inscribed in the isosceles triangle with sides 5cm, 5cm, and 6cm is approximately 2.89 cm.
36 minus 20 minus 32 times 1/4
Answers
Answer:
6
Step-by-step explanation:
36 - 20 - 32 x 1/4
=> 36 - 20 - 32/4
=> 36 - 20 - 8
=> 36 - 28
=> 6
Pilar has 40 shells in her collection. She goes to the beach. She collects 6 more shells in the morning and 3 more shells in the afternoon. What is the percent change in Pilar's shell collection from the beginning of the day to the end? Show your work.
Answers
The percent change in Pilar's shell collection from the beginning of the day to the end is, 22.5%
What is the percentage?Percentage is a way to express a number as a fraction of 100. It is often used to represent ratios and proportions in a more convenient and understandable form, especially in financial and statistical contexts. For example, 50% means 50 per 100, or half of a given quantity. It is denoted using the symbol "%".
Given that,
Pilar has 40 shells in her collection.
She collects 6 more shells in the morning and 3 more shells in the afternoon.
The percent change in Pilar's shell collection from the beginning of the day to the end = ?
At the beginning of the day, Pilar has 40 shells.
In the morning, she collects 6 more shells, bringing her total to
= 40 + 6
= 46 shells.
Then, in the afternoon, she collects 3 more shells, bringing her total to
=46 + 3
= 49 shells.
To find the percent change in Pilar's shell collection from the beginning of the day to the end, we can use the formula:
percent change = (final value - initial value) / initial value * 100%
Plugging in the values we have:
percent change = (49 - 40) / 40 x 100%
percent change = 9 / 40 x 100%
percent change = 22.5%
Therefore, there is a 22.5% increase in Pilar's shell collection from the beginning of the day to the end.
To know more about Percentage check:
https://brainly.com/question/29306119
#SPJ1
The sequence -4,-6,-8,-10 has a constant ratio or difference of
Answers
Answer:
2
Step-by-step explanation:
We can subtract to find the common difference.
-4 - (-6) = 2
-6 - (-8) = 2
-8 - (-10) = 2
As you can see it is constant.
Best of Luck!
Plz help
.
X
X
X
X
D
E
D
D
D

Answers
Answer:
radius by 2 ye this will be the correct answer d=r/2
Can someone help me!!!

Answers
formula:
l(length) x w(width)

An electrician charges $80 for a service call, and then $100/hr for labor. Find the linear equation that models the cost based on the number of labor hours. How much will it cost for 3 ½ hours of the electrician’s time?
Answers
If the first two terms of a geometric sequence are 16 and 24, which of the following is the value of the fourth term?
a. 32
b. 36
c. 40
d. 54
Answers
Answer:
D. 54
Step-by-step explanation:
Remember that for geometric series, it's a progression by multiplication. From the first term, you multiply by your common ratio to get each successive term.
\(a_{n}\) = \(ar^{n-1}\)
In which \(a_{n}\) is the nth term in a sequence.
A is the first term.
And R is the common ratio.
The common ratio is 1.5. Which was found by dividing 24 by 16.
Our equation would now be : \(16*1.5^{n-1}\)
By replacing n with 4, you will get 54.
Or, if we multiply each term by 1.5, you will end up with 54 by the time you reach the fourth term.
Hope this helps mate.
Determine how many integer solutions there are to
x₁ + x₂ + x3 + x₁ = 20, if
0≤x₁ < 3, 0≤ x₂ < 4, 0≤x3 <5, 0≤x4 < 6
Answers
Based on the information given, there are a total of 118 solutions.
How many possible solutions are there?This is a problem of solving a Diophantine equation subject to some conditions. Let's introduce a new variable y4 = 20 - (x1 + x2 + x3 + x4). Then the problem can be restated as finding the number of solutions to:
x1 + x2 + x3 + y4 = 20
Subject to the following conditions:
0 ≤ x1 < 3
0 ≤ x2 < 4
0 ≤ x3 < 5
0 ≤ y4 < 6
We can solve this problem using the technique of generating functions. The generating function for each variable is:
(1 + x + x^2) for x1
(1 + x + x^2 + x^3) for x2
(1 + x + x^2 + x^3 + x^4) for x3
(1 + x + x^2 + x^3 + x^4 + x^5) for y4
The generating function for the equation is the product of the generating functions for each variable:
(1 + x + x^2)^3 (1 + x + x^2 + x^3 + x^4 + x^5)
We need to find the coefficient of x^20 in this generating function. We can use a computer algebra system or a spreadsheet program to expand the product and extract the coefficient. The result is: 1118
Learn more about solutions in https://brainly.com/question/30665317
#SPJ1
Answer: This problem involves finding the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints. We can use the stars and bars method to solve this problem.
Suppose we have 20 stars representing the sum x₁ + x₂ + x3 + x₁. To separate these stars into four groups corresponding to x₁, x₂, x₃, and x₄, we need to place three bars. For example, if we have 20 stars and 3 bars arranged as follows:
**|**||
then the corresponding values of x₁, x₂, x₃, and x₄ are 2, 4, 6, and 8, respectively. Notice that the position of the bars determines the values of x₁, x₂, x₃, and x₄.
In general, the number of ways to place k identical objects (stars) into n distinct groups (corresponding to x₁, x₂, ..., xₙ-₁) using n-1 separators (bars) is given by the binomial coefficient (k+n-1) choose (n-1), which is denoted by C(k+n-1, n-1).
Thus, the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints is:
C(20+4-1, 4-1) = C(23, 3) = 1771
However, this count includes solutions that violate the upper bounds on x₁, x₂, x₃, and x₄. To eliminate these solutions, we need to use the principle of inclusion-exclusion.
Let Aᵢ be the set of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints, where xᵢ ≥ mᵢ for some integer mᵢ. Then, we want to find the cardinality of the set:
A = A₀ ∩ A₁ ∩ A₂ ∩ A₃
where A₀ is the set of all non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20, and Aᵢ is the set of solutions that violate the upper bound on xᵢ.
To find the cardinality of A₀, we use the formula above and obtain:
C(20+4-1, 4-1) = 1771
To find the cardinality of Aᵢ, we subtract the number of solutions that violate the upper bound on xᵢ from the total count. For example, to find the cardinality of A₁, we subtract the number of solutions where x₂ ≥ 4 from the total count. To count the number of solutions where x₂ ≥ 4, we fix x₂ = 4 and then count the number of solutions to the equation x₁ + 4 + x₃ + x₄ = 20 subject to the constraints 0 ≤ x₁ < 3, 0 ≤ x₃ < 5, and 0 ≤ x₄ < 6. This count is given by:
C(20-4+3-1, 3-1) = C(18, 2) = 153
Similarly, we can find the cardinalities of A₂ and A₃ by fixing x₃ = 5 and x₄ = 6, respectively. Using the principle of inclusion-exclusion, we obtain:
|A| = |A₀| - |A
Step-by-step explanation:
Could somebody help me solve this step-by-step? I'm stuck


Answers
Answer:
[1, 3]
Step-by-step explanation:
g(x) = f(2x), so g(x) is f(x) compressed horizontally by a factor of 2. Vertically, it is not changed.
Therefore, the ranges are identical.
work out the area of the shape

Answers
Answer:
45cm^2
Step-by-step explanation:
we have two shapes in the diagram a square and a triangle so we find the area of each of them and add them together
finding the area of a square
we have area= s×s
area = 7×5
area = 35cm^2
finding the area of a triangle
1/2 ×b×h
1/2×4×5
area = 10cm^2
so we add together
total area = 35+ 10
area = 45cm^2
Determinar los pasos para encontrar el conjunto solucion de una ecuacion lineal en una variable

Answers
Una ecuación es una igualdad matemática entre dos expresiones algebraicas
Pasos para resolver una ecuacion lineal de una sola variable:
0. Resolver el denominador en caso de ser una fraccion.
,1. Resolver las operaciones presentes dentro de los paréntesis
,2. Agrupar los terminos con variable a un lado y los terminos independientes en el otro.
,3. Reducir los terminos semejantes
,4. Despejar la variable.

The length of a rectangle is 5 cm less than 3 times its width. If the perimeter is 54 cm, find its length.
Answers
Answer:
W = 8cm
L = 19cm
Step-by-step explanation:
The first step to solving these problems is always writing the information that is given into 2 equations.
Piece of info #1: Length is 5cm less than 3 times the width
Piece of info #2: Perimeter (of the rectangle, which has 4 sides) is 54cm
Turing these into equations...
Equation 1) L = 3*W - 5
Equation 2a) L+L+W+W = 54
Let's simplify that second equation:
Equation 2b) 2L+2W = 54
Now, we just solve the system of two equations by substitution. Take the known value of L from equation 1 and substitute it in for the value of L in equation 2b:
2*(3*W-5)+2W = 54
Now we solve for W:
6W - 10 + 2W = 54
8W - 10 = 54
8W = 64
W = 64/8
W = 8 cm
Now that we know W, we can substitute its value into either equation 1 or equation 2 to find L. Here, I'll randomly choose equation 1.
Equation 1) L = 3*W - 5
L = 3*8 - 5
L = 24-5
L = 19 cm
Use a symbolic method to solve each equation. Show each solution exactly as a rational or a radical expression

Answers
Here, we want solve for the value of x
We proceed as follows;
Firstly, we divide both sides by the minus sign
\((x-1)^2\text{ = 17}\)Now, we find the square roots of both sides;
\(\begin{gathered} (x-1)\text{ = }\pm\sqrt[]{17} \\ x\text{ = 1+}\sqrt[]{17}\text{ or 1-}\sqrt[]{17} \end{gathered}\)please help :) thanks !

Answers
Answer:
Step-by-step explanation:
b
What the meaning of statement this?

Answers
Axiom of Infinity states that there is at least one set that contains an infinite number of elements.
A basic tenet of set theory, the Axiom of Infinity affirms the existence of an endless set. In plainer language, it proves that at least one set has elements with an infinite number.
This axiom is crucial because it enables rigorous and consistent mathematical reasoning about and interaction with infinite collections. It offers a fundamental premise for many infinity-related mathematical notions and structures, including infinite sequences, series, and cardinality.
The Axiom of Infinity ensures that mathematics is not restricted to only finite quantities and allows for the exploration of the rich and intriguing realm of infinite structures by declaring the existence of an endless set.
Learn more about axiom here:
https://brainly.com/question/31203196
#SPJ1
Anne bought a piece of ribbon that is 7 over 9 m long. She used 3 over 18 m of it to tie a birthday present. She then used the remaining ribbon to form squares of sides 1 over 16 m. What was the maximum number of squares she could form?
Answers
Answer:
9 squares
Step-by-step explanation:
Anne bought a piece of ribbon = 7 over 9 m long = 63 m²
she used = 3 over 18 m = 54 m²
left = 9 m²
maximum number of squares she could form of 1 m = 9
i need help with this equation: p+9=-1
Answers
Answer:
p = - 10
Step-by-step explanation:
Step 1:
p + 9 = - 1 Equation
Step 2:
p = - 1 - 9 Subtract 9 on both sides
Answer:
p = - 10
Hope This Helps :)
What is the total surface of the pyramid in square centimeters? A: 17.5 B:70 C:140 D:35

Answers
Answer:
C:140
Step-by-step explanation:
because 7 x 5 in the tiangle.
some adults and children are watching a musical there are n children there are 25 fewer adults
Answers
According to the concept of algebraic expression and arithmetic, the correct answers are A) Number of adults = N - 25. B) Number of adults when N = 124: 124 - 25 = 99
A) Let's denote the number of children as N. Since there are 25 fewer adults than children, the number of adults can be expressed as N - 25.
B) If there are 124 children, we substitute N with 124 in the expression from part A. Thus, the number of adults would be 124 - 25 = 99.
To arrive at these answers, we used the given information that there are "N" children and 25 fewer adults than children. By substituting the value of N, we determined the number of adults in terms of N and then calculated the specific number of adults when N is equal to 124.
Note: The given question is incomplete. The complete question is:
Some adults and children are watching a musical. there are 'N' number of children. There are 25 fewer adults than children.
A) find the number of adults in terms of 'N'.
B) if there are 124 children how many adults are there?
For more questions on algebraic expression:
https://brainly.com/question/29333936
#SPJ8
100%
Which is true?
O A. 2.01 < 2.2
B. 0.060 > 0.1
O C. 3.259 < 3.2
D. 0.088 > 0.098
E. 9.9 > 10.01
Due right now like now
Answers
Answer:
A
Step-by-step explanation:
2.2 IS GREATER THAN 2.01
help fast pleaseeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
40 x 18 = 720
Step-by-step explanation:
Hope this is what you need! =)
How many hours would it take Natalie if she worked alone?

Answers
Given the following exponential function, identify whether the change represents growth or decay, and determine the percentage rate of increase or decrease.
y=57(0.4)^x
Answers
Answer:
Decay, 60%
Step-by-step explanation:
Remember that the exponential function is written in the form \(y=ab^x\). In this problem, a=57 and b=0.4. A function is considered a growth function when \(b>1\). Since 0.4 not greater than 1, this is an exponential decay function.
Now, to find the rate of decrease we can use part of the form \(y=a(1-r)^x\).
\(1-r\) represents the percentage decrease, in this case, 0.4. If that entire term is 0.4, we need to solve for \(r\).
\(1-r=0.4\\r=0.6\)
So, the rate of percentage decrease is 60%.
I hope this helps!
