Guys please solve 3-3(2x+1)+8x≥ 3 − 3
Answers
Step-by-step explanation:
3-3(2x+1)+8x>=3-3
3-3*2x-3*1+8x>=0
3-3-6x+8x>=0
2x>=0
x>=0
Related Questions
Chandler decided to go cliff jumping into the lake at his cottage. He started on the cliff at 32 ft above sea level. He jumped for 40 feet! How far below sea level did Chandler end up?
Answers
Chandler ended up 8 feet below sea level. The negative sign indicates that his final position is below sea level. This means that he has descended further into the lake compared to the starting point on the cliff.
Chandler started on the cliff at 32 feet above sea level. When he jumped for 40 feet, we need to determine the final position in relation to sea level.
Since Chandler jumped down, the distance below sea level will be calculated as a negative value. To find how far below sea level Chandler ended up, we subtract the jump distance (40 feet) from the starting height (32 feet above sea level):
32 feet - 40 feet = -8 feet
It's important to note that negative values are used here to represent the direction and magnitude of Chandler's descent relative to sea level
For more such questions on feet
https://brainly.com/question/30403118
#SPJ8
Answer:
-8 feet
Step-by-step explanation:
Evaluate [log2(3)].[log3(4)].[log4(5)]...[log63(64)]. (Note here that 62 logarithmic terms are being multiplied together.) 1 614985 2020
Answers
Evaluating [log2(3)].[log3(4)].[log4(5)]...[log63(64)] is 6
How to evaluate the logarithmic termsWe can use the property that [log_a(b)]=[log_c(b)/log_c(a)] to simplify the expression. Applying this property repeatedly, we get:
[log2(3)].[log3(4)].[log4(5)]...[log63(64)]
= [log2(3)/log2(2)].[log3(4)/log3(3)].[log4(5)/log4(4)]...[log63(64)/log63(62)]
= [log2(3)/1].[log3(4)/1].[log4(5)/1]...[log63(64)/1]
= log2(3) log3(4) log4(5) ... log63(64)
Now, we can use the identity [log_a(b)log_b(c)log_c(d)...log_y(z)] = log_a(z) to combine the logarithms into a single logarithm with a base of 2:
log2(3) log3(4) log4(5) ... log63(64) = log2(64)
Since 2^6 = 64, we have:
log2(64) = 6
Therefore, [log2(3)].[log3(4)].[log4(5)]...[log63(64)] evaluates to 6.
learn more about logarithmic terms at:https://brainly.com/question/25710806
#SPJ1
|3y - 7| - 10 = -5 solve for y:
Answers
Answer: y=1.25
Step-by-step explanation:
First things first you have to find what is in the bracket things (i don’t know what it’s called) So 3 - 7 is -4y but since it’s absolute it’s going to be 4y.
So now you’ve got 4y - 10 = -5. Your going to want to eliminate 10 so, subtract 10 to both sides giving you 4y = -5
Lastly to get y by itself you need to divide it by its self so, 4y divided by 4. Do it to both sides. This gives you…
Y = 1.25
While problem and solution essays are considered expository (writing that exposes facts) in nature, they are persuasive in nature because they call for ____________ to a problem. Evidence An explanation A solution
Answers
While problem and solution essays are considered expository (writing that exposes facts) in nature, they are persuasive in nature because they call for a solution to a problem.
What is the problem?
A mathematical problem is one that can be modeled, examined, and potentially resolved using mathematical techniques. This can be a practical issue, like figuring out the orbits of the planets in our solar system, or a more theoretical issue, like Hilbert's problems.
The expository essay is a type of essay that calls for the student to research a topic, assess the evidence, elaborate on the topic, and present an argument about the topic in a clear and succinct manner. This can be done by using examples, definitions, comparisons, cause and effect analyses, and more.
To learn more about a solution, click on the below link:
https://brainly.com/question/4364712
#SPJ1
can a quadratic function have both a maximum value and a minimum value?
Answers
No, a quadratic function cannot have both a maximum value and a minimum value.
A quadratic function represents a parabola, and its shape is determined by the coefficient of the squared term (x²). If the coefficient is positive, the parabola opens upward, and if it is negative, the parabola opens downward. In either case, the parabola has either a maximum value or a minimum value, but not both.
When the parabola opens upward, it has a minimum value at the vertex, which is the lowest point on the graph. Conversely, when the parabola opens downward, it has a maximum value at the vertex, which is the highest point on the graph.
Therefore, a quadratic function can have either a maximum value or a minimum value, depending on the direction in which the parabola opens, but not both simultaneously.
Kindly Heart and 5 Star this answer and especially don't forgot to BRAINLIEST, thanks!Answer:
no it cant
Step-by-step explanation:
Find the arc length AB
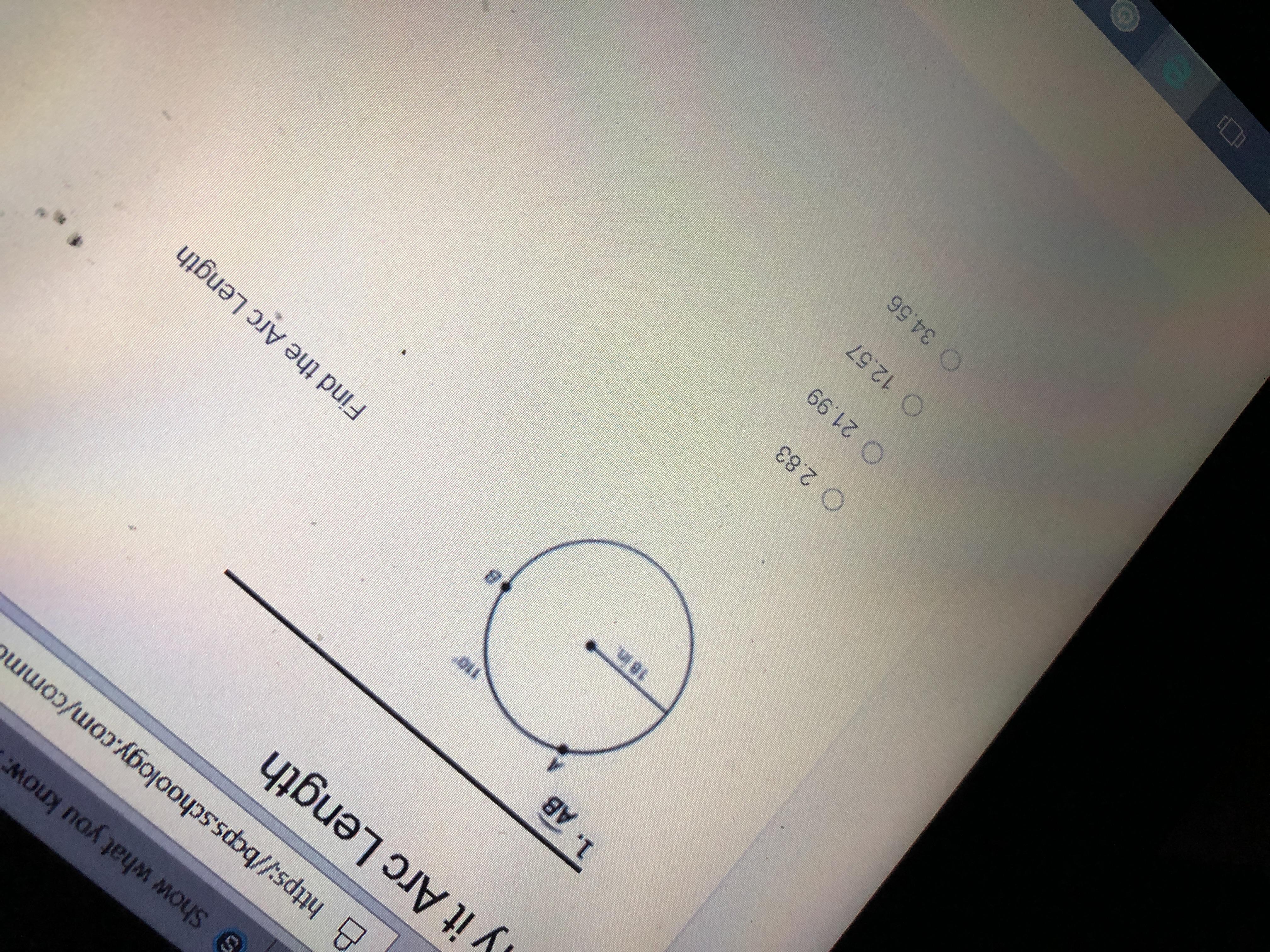
Answers
Answer :
34.56
I hope it helps

If the graph passes the horizontal-line test, then the function is one-to-one. Functions that are one-to-one have inverses that are also functions. Therefore, the inverse is a function. Compare your response to the sample response above. What did you include in your explanation? a reference to the horizontal-line test a statement that the function is one-to-one the conclusion that the inverse is a function
Answers
Based on the sample response given, the statements included in the explanation on the horizontal line test are:
a reference to the horizontal-line test.a statement that the function is one-to-one. inverse is a function.What is the horizontal-line test?The horizontal line test is used to not only find out if a graph has an inverse function, but also if that inverse is also a function itself.
To pass the horizontal line test, the function has to be one-to-one which means that a horizontal line can intersect the graphed function at one point in all places. If this happens, then there is an inverse and the inverse itself is a function.
Find out more on the horizontal line test at https://brainly.com/question/11471811
#SPJ1
A company created a new container in the shape of a
triangular prism that will hold sunflower seeds. A three-
dimensional image of the container is shown below, as
well as a two-dimensional image of the base.
6 in.
3.2 in.
2 in.
3.2 in.
1 in.
square inches
1 in.
The container will be made from cardboard. How many
square inches of cardboard are needed to make one
container? Assume there are no overlapping areas.

Answers
The number of square inches of cardboard that are needed to make one
the container is 18.
We have,
The volume of the triangular prism.
= Area of the triangle x height
Now,
Height = 6 in
And,
To find the area of a triangle, we can use Heron's formula.
A = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case, the side lengths of the triangle are 3.2 in, 3.2 in, and 2 in.
Let's calculate the area using Heron's formula:
s = (3.2 + 3.2 + 2) / 2 = 4.2
A = √(4.2(4.2 - 3.2)(4.2 - 3.2)(4.2 - 2))
A = √(4.2 x 1 x 1 x 2.2)
A = √(9.24)
A ≈ 3.04 square inches
Now,
The volume of the triangular prism.
= Area of the triangle x height
= 3.04 x 6
= 18.24 in²
Now,
Area of one cardboard.
= 1² in²
= 1 in²
Now,
The number of square inches of cardboard that are needed to make one
container.
= The volume of the triangular prism / Area of one cardboard
= 18.24 in² / 1 in²
= 18.24
= 18
Therefore,
The number of square inches of cardboard that are needed to make one
the container is 18.
Learn more about Prism here:
https://brainly.com/question/12649592
#SPJ1
HELP ASAP!!!The first picture is what each variables equal too


Answers
Answer:
Just replace the variables with the number
d5
c4 (uh oh)
a2
b-3
f-7
d-c = 5 - 4 = 1
1/3 - 4(ab+f)
2 x -3 = -6
-6 + -7 = -13
-13 x 4 = -52
1/3 - -52 = 1/3 + 52 =
52 1/3
Hope this helps
Step-by-step explanation:
Help me asap and need the answer quick

Answers
Answer:20 m/s
Step-by-step explanation:
Answer:
20 m/s
Step-by-step explanation:
700 ÷ 35 = 20 m/s
Based on previous research, the standard deviation of the distribution of the age at which children begin to walk is estimated to be 1.5 months. A random sample of children will be selected, and the age at which each child begins to walk will be recorded. A 99% confidence interval for the average age at which children begin to walk will be constructed using the data obtained from the sample of children. Of the following, which is the smallest sample size that will result in a margin of error of 0.1 month or less for the confidence interval?
a. 400.
b. 900.
c. 1,300.
d. 1,600.
e. 2,100.
Answers
Answer:
d. 1,600.
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.99}{2} = 0.005\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.005 = 0.995\), so Z = 2.575.
Now, find the margin of error M as such
\(M = z\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
Based on previous research, the standard deviation of the distribution of the age at which children begin to walk is estimated to be 1.5 months.
This means that \(\sigma = 1.5\)
Of the following, which is the smallest sample size that will result in a margin of error of 0.1 month or less for the confidence interval?
The sample size has to be n or larger. n is found when \(M = 0.1\). So
\(M = z\frac{\sigma}{\sqrt{n}}\)
\(0.1 = 2.575\frac{1.5}{\sqrt{n}}\)
\(0.1\sqrt{n} = 2.575*1.5\)
Multiplying both sides by 10
\(\sqrt{n} = 2.575*15\)
\((\sqrt{n})^2 = (2.575*15)^2\)
\(n = 1492\)
So the sample size has to be at least 1492, which means that of the possible options, the smallest sample size is 1600, given by option d.
The sample size should be at least 1492, So the possible options, the smallest sample size is 1600, option D is the correct answer
Based on previous research, the standard deviation of the distribution of the age at which children begin to walk is estimated to be 1.5 months. A random sample of children will be selected, and the age at which each child begins to walk will be recorded. A 99% confidence interval for the average age at which children begin to walk will be constructed.
What is the margin of error?
The margin of error tells you how many percentages points your results will differ from the real population value.
\(M=z\frac{\sigma}{\sqrt{n} }\)
We need to find our α level, that is the subtraction from 1 by the confidence interval for the average age divided by 2.
\(\alpha = \frac{1-0.99}{2}\\ =0.005\)
Now, we need to find z which is 1-α
\(1-\alpha \\=1-0.005\\\rm z=2.575\)
The margin of error M
\(M=z\frac{\sigma}{\sqrt{n} }\)
Here, \(\sigma\) is the standard deviation of the population.
n is the size of the sample.
So,
\(\rm M=z\frac{\sigma}{\sqrt{n} } \\\rm0.1=2.575\frac{1.5}{\sqrt{n} } \\\rm0.1\times\sqrt{n} =2.575\times{1.5}\\\rm\sqrt{n} =2.575\times{1.5}\\\rm(\sqrt{n} )^{2} =(2.575\times{1.5})^{2} \\\rm n=1492\)
Hence, the sample size should be at least 1492, So the possible options, the smallest sample size is 1600, option D is the correct answer.
Learn more about the margin of error here:
https://brainly.com/question/6979326
WILL GIVE BRAINLIEST!!
If the length of a rectangle is decreased by 4 cm and the width is increased by 5 cm, the result will be a square, the area of which will be 40 cm2 greater than the area of the rectangle. Find the area of the rectangle.
Answers
Answer:
\(\huge\boxed{\sf Area = 12.8 cm\²}\)
Step-by-step explanation:
Let,
The length of rectangle = x
The width of rectangle = y
The length of square = x - 4
The width of square = y + 5
Area of rectangle = xy
Area of square = xy + 40
Condition No. 1:
Area of Square = Length of square * Width of square
xy + 40 = (x - 4)(y - 5)
xy + 40 = xy - 5x - 4y + 20
- 5x - 4y = 40 - 20
- 5x - 4y = 20
5x + 4y = -20 ------------------(1)
Condition No. 2:
We know that:
Length of square = Width of square
x - 4 = y + 5
Add 4 to both sides
x = y + 5 + 4
x = y + 9 ---------------------------(2)
Solution:
Put Eq. (2) in (1)
5 (y + 9) + 4y = -20
5y + 45 + 4y = -20
9y + 45 = -20
9y = -20-45
y = -65 / 9
Now, Put the value of y in Eq. (2)
x = (-65 / 9) + 9
x = (-65 + 81) / 9
x = 16 / 9 cm
Now,
Area of rectangle = xy
Area = ( -65 / 9 ) * ( 16 / 9 )
Area = (-65*16) / (9*9)
Area = -1040/81
Area = 12.8 cm² (Neglecting -ve sign)
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Answer:
360
Step-by-step explanation:
360m^2
In an insect colony, there are 270 insects after 7 days. If there were initially 80 insects, how long will it take the population to grow to 700 insects?
Answers
Step-by-step explanation:
Total insects = 270
Days = 7
If 80 insects to 700 insects
Days = 700 ÷ 80 = 8.75
It will take 8.75 days
hay 1230 personas, entre hombres y mujeres. Si se sabe que el número de mujeres, supera en 150 al número de hombres. ¿Cuántos hombres están habitando la mini ciudad?
Answers
There are 540 men living in the mini city.
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
Therefore, there are 540 men living in the mini city.
To check our answer, we can substitute x = 540 into our original equation:
540 + (540 + 150) = 1230
690 = 1230
This is false, so there must be an error in our calculation. We can double-check our work by trying a different approach.
We know that the number of women exceeds the number of men by 150, so we can represent the number of women as (x + 150). We also know that the total number of people is 1230, so we can set up an equation:
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
For such more questions on mini
https://brainly.com/question/29266607
#SPJ8
Original price of a jacket: $269.50
Discount: 247
Tax: 6%
Answers
A rock is thrown from the top of a building. The height s (in feet) as a function of time (in seconds) can be modeled by the function
s(t) = -16t² + 3000
Approximately when will the rock be 1,976 feet above the ground.
O a
Ob
C
8 sec
135 sec
85 sec
15 sec
Answers
Answer: the rock will be at a height of 1,976 feet above the ground after approximately 8 seconds
Step-by-step explanation:
We can start by setting the height function equal to 1,976 and solving for t:
-16t² + 3000 = 1976
Subtracting 1976 from both sides, we get:
-16t² + 1024 = 0
Dividing both sides by -16, we get:
t² - 64 = 0
Factoring, we get:
(t + 8)(t - 8) = 0
So t = 8 or t = -8. We can ignore the negative solution since time cannot be negative.
Therefore, the rock will be at a height of 1,976 feet above the ground after approximately 8 seconds.
Answer: (A) 8 sec
Luzia ran the 400-meter race 3 times. Her fastest time was 52.3 seconds. Her slowest time was 56.3 seconds. If Luzia’s average time was 54.0 seconds, what was her time for the third race?
Answers
Answer: 53.5 seconds
Step-by-step explanation:
Question 11 of 45
Which similarity postulate or theorem can be used to verify that the two
triangles shown below are similar?
12
6 R
X 2 z
O A. Similarity cannot be determined,
B. SSS theorem
O C. AA postulate
D. SAS theorem

Answers
Answer:
You are only given a Side, an Angle, and then a side. So that is what I would choose. It can't be AA because you weren't given two angles. It can't be SSS because you weren't given 3 sides.
Step-by-step explanation:
ΔPQR and ΔXYZ are similar due to the SSS theorem.
Option B is the correct answer.
What is triangle congruency?There are ways to prove that two triangles are congruent.
- Side-Side-Side (SSS) Congruence.
The three sides of one triangle are equal to the corresponding three sides of another triangle.
- Side-Angle-Side (SAS) Congruence.
The two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle.
- Angle-Side-Angle (ASA) Congruence.
The two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle.
- Angle-Angle-Side (AAS) Congruence.
We have,
Similar triangles are triangles that have the same shape but may have different sizes.
Two triangles are similar if their corresponding angles are equal, and their corresponding sides are proportional.
When two triangles are similar, they have the same shape, but one may be larger or smaller than the other.
Now,
ΔPQR and ΔXYZ
PQ/XY = 12/4 = 3
PR/XZ = 6/2 = 3
Since the two sides are proportional,
QR/YZ will be proportional.
Now,
PQ/XY = PR/XZ = QR/YZ
ΔPQR and ΔXYZ are similar due to the SSS theorem.
Thus,
ΔPQR and ΔXYZ are similar due to the SSS theorem.
Learn more about triangle congruency here:
https://brainly.com/question/12413243
#SPJ7
A rectangular prism has a volume of 330 cubic feet. The prism is 6 feet long and 4 feet wide. What is the height of the prism? Show two different ways to find the height
Answers
Answer:
H =13.75 ft
Step-by-step explanation:
First, 6 x 4 = 24. To find the height you need to do 330/ 24 which = 13.75
In a popular online role playing game, players can create detailed designs for their character's "costumes," or appearance. Isabella sets up a website where players can buy and sell these costumes online. Information about the number of people who visited the website and the number of costumes purchased in a single day is listed below.
105 visitors purchased no costume.
41 visitors purchased exactly one costume.
8 visitors purchased more than one costume.
Based on these results, express the probability that the next person will purchase one or more costumes as a decimal to the nearest hundredth.
Answers
The probability that the next person will purchase one or more costumes can be found by dividing the number of visitors who purchased one or more costumes by the total number of visitors.
The total number of visitors is 105 + 41 + 8 = 154.
The number of visitors who purchased one or more costumes is 41 + 8 = 49.
So the probability that the next person will purchase one or more costumes is 49/154, which is approximately 0.32 to the nearest hundredth.
I WILL GIVE 50 POINTS FOR AN ANSWER The daily cost of hiring a clown, y, to work x hours at a birthday party can be modeled using a linear function. The clown charges a fixed cost of $50 for booking plus an additional cost of $15 per hour. The clown works a maximum of 6 hours per day.
For one day of work, what is the range for this situation?
Answers
PLEASE HELP!! a bag contains 10 marbles. four of them are red, three blue, two white, and one yellow. A mare ke drawn at random. What is the probability that it is blue?

Answers
Answer:
The probability that one marble drawn at random is not blue is 70%
the monthly salaries (in thousands of dollars) for a sample of 7 employees of a firm are: 9, 7, 8, 7, 10, 11 and 11. which of the following statements is true about the mean, median and mode?
Answers
For the given monthly salaries of the 7 employees of the firm , then the true statement is : (a) mean = median .
In statistics the Mean is defined as sum of a collection of numbers divided by count of numbers .
the given monthly salaries is 9, 7, 8, 7, 10, 11 and 11.
arranging the data in ascending order ,
we get ; 7 , 7 , 8 , 9 , 10 , 11 , 11 .
the sum of the salaries is = 63 ;
So , the mean is = 63/7 = 9 .
median is the middle term of the given data that is = 9 ;
the mode is the most times occurred frequency that is 7 and 11 .
On comparing the mean , mode and median ,
we get ; mean = median .
Therefore , the correct statement is (a) mean = median .
The given question is incomplete , the complete question is
The monthly salaries (in thousands of dollars) for a sample of 7 employees of a firm are: 9, 7, 8, 7, 10, 11 and 11.
Which of the following statements is true about the mean, median and mode ?
(a) mean = median
(b) mode < median < mean
(c) mode < mean < median
(d) mode = median = mode .
Learn more about Mean here
https://brainly.com/question/29990080
#SPJ4
Find a point-slope form for the line with slope 1/5 and passing through the point (-2,-1)
Answers
An = a1 r (n-1)
An > nth term (missing term)A1 > fist termr > common ration > ordinal number of the missing term in the sequence 3,6,12,24,48_____An =a1 r (n-1) > 6th term = (3)[2{6-1}] A n= 6th term 6th term = (3)(25)A1 = 3 6th term = (3) (32)r = 2 6th term = 96 n = 6Step-by-step explanation:
hope lessconsider applying critical-word first and early restart on l2 cache misses. assume a 1 mb l2 cache with 64 bytes blocks. with critical-word first, it takes 100 cycles to get the first 8-byte word. otherwise, the time to receive the first 8 bytes from the memory is 90 cycles. each additional 8 bytes from the main memory require 10 cycles. if no early restart, then any word is only accessible after the block is fully fetched. further assume that the probability of referencing the first word (64-bit wide) in a block is 30% while the rest are referenced with equal probability.
Answers
The average access time for a cache miss is decreased from 61 cycles to 116 cycles by using critical-word first and early restart, which is a considerable improvement.
Critical-word first and early restart are two approaches we can employ to enhance the L2 cache's performance.
The first word in the cache block is accessed first when using the critical-word first strategy to reduce latency. In our scenario, getting the first 8-byte word requires 100 cycles. So, to speed up access when a cache miss occurs, the critical word should be fetched first.
The number of blocks in the cache can be determined using the formula below, assuming a 1 MB L2 cache with 64-byte blocks:
1 MB = 1024 * 1024 bytes
Number of blocks = 1 MB / 64 bytes = 16384
The first 8 bytes from memory must be retrieved in 90 cycles, and each subsequent 8 bytes must be retrieved in 10 cycles. The duration needed to fetch the complete block therefore is:
Time to fetch block = 90 cycles + 7 * 10 cycles = 160 cycles
Now, With the critical-word first and early restart, let's compute the average access time for a cache miss with and without these features.
Without critical-word first and early restart:
The probability of referencing the first word in a block is 30%.
The probability of referencing the remaining words in a block is (1 - 0.3) / 7 = 0.1.
So, When a cache miss occurs without using critical-word first and an early restart, the average access time is:
Average access time = probability of referencing first word * time to fetch critical word + probability of referencing remaining words * time to fetch block
= 0.3 * 90 cycles + 0.1 * 160 cycles
= 45 cycles + 16 cycles
= 61 cycles
With critical-word first and early restart:
The essential word is retrieved first, which requires 100 cycles.
As soon as the required data is made available, we begin accessing it.
In the background, the remaining words in the block are fetched.
With critical-word first and an early restart, the average access time for a cache miss is as follows:
Average access time = time to fetch critical word + probability of referencing remaining words * time to fetch block
= 100 cycles + 0.1 * 160 cycles
= 100 cycles + 16 cycles
= 116 cycles
Therefore, The average access time for a cache miss is decreased from 61 cycles to 116 cycles by using critical-word first and early restart, which is a considerable improvement.
To learn more about probability , visit the link below:
https://brainly.com/question/13957582
#SPJ4
The circumference of a circle is 15pi centimeters what is the area of the circle in terms of pi?
Answers
\(\textit{circumference of a circle}\\\\ C=2\pi r ~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ C=15\pi \end{cases}\implies 15\pi =2\pi r\implies \cfrac{15\pi }{2\pi }=r\implies \cfrac{15}{2}=r \\\\[-0.35em] ~\dotfill\\\\ \textit{area of a circle}\\\\ A=\pi r^2 \begin{cases} r=radius\\[-0.5em] \hrulefill\\ r=\frac{15}{2} \end{cases}\implies A=\pi \left( \cfrac{15}{2} \right)^2\implies A=\cfrac{225\pi }{4}\implies A=56.25\pi\)
One card is selected from a standard deck of 52 cards. Find the following probabilities. Round to the
nearest hundredth if necessary.
Event
12. The the probability of selecting a spade
or a six
13. The probability of selecting a black card
or a jack
14. The probability of selecting a seven or a
face card
15. The probability of selecting a face card
or a queen
16. The probability of selecting a four or a
king
Work
Answer

Answers
Answer:
12. The probability of selecting a spade or a six: There are 13 spades and four sixes in a standard deck of 52 cards. However, one of the cards (the six of spades) is counted twice. Therefore, the total number of cards that are either spades or sixes is 13 + 4 - 1 = 16. So, the probability of selecting a spade or a six is 16/52 = 4/13.
13. The probability of selecting a black card or a jack: There are 26 black cards and four jacks in a standard deck of 52 cards. However, two of the cards (the jack of clubs and the jack of spades) are counted twice. Therefore, the total number of cards that are either black cards or jacks is 26 + 4 - 2 = 28. So, the probability of selecting a black card or a jack is 28/52 = 7/13.
14. The probability of selecting a seven or a face card: There are four sevens and 12 face cards (which include jacks, queens, and kings) in a standard deck of 52 cards. However, three of the cards (the jack, queen, and king of hearts) are counted twice. Therefore, the total number of cards that are either sevens or face cards is 4 + 12 - 3 = 13. So, the probability of selecting a seven or a face card is 13/52 = 1/4.
15. The probability of selecting a face card or a queen: There are 12 face cards and four queens in a standard deck of 52 cards. However, one of the cards (the queen of hearts) is counted twice. Therefore, the total number of cards that are either face cards or queens is 12 + 4 - 1 = 15. So, the probability of selecting a face card or a queen is 15/52 = 15/52.
16. The probability of selecting a four or a king: There are four fours and four kings in a standard deck of 52 cards. However, one of the cards (the king of hearts) is counted twice. Therefore, the total number of cards that are either fours or kings is 4 + 4 - 1 = 7. So, the probability of selecting a four or a king is 7/52 = 1/7.
The unit circle below shows 100∘ and -100∘. Find the values below, rounded to three decimal places if necessary.

Answers
Answer:
sin(100°) = 0.985
sin(-100°) = -0.985
Step-by-step explanation:
In a unit circle, each point (x, y) on the circumference corresponds to the coordinates (cos θ, sin θ), where θ represents the angle formed between the positive x-axis and the line segment connecting the origin to the point (x, y).
Therefore, sin(100°) equals the y-coordinate of the point (-0.174, 0.985), so:
\(\boxed{\sin(100^{\circ}) = 0.985}\)
Similarly, sin(-100°) equals the y-coordinate of the point (-0.174, -0.985), so:
\(\boxed{\sin(-100^{\circ}) = -0.985}\)
In the unit circle the value of sin (100) = 0.985 and the value of sin (-100) = -0.985, in three decimal places.
What is the value of sine of the angles?The value of the sine of the angles is calculated by applying the following formula as follows;
The value of sin (100) is calculated as follows;
sin(100°) corresponds to the y-coordinate of the point (-0.174, 0.985) as given on the coordinates of the unit circle.
sin (100) = 0.985
The value of sin (-100) is calculated as follows;
sin(100°) corresponds to the y-coordinate of the point (-0.174, -0.985), as given on the coordinates of the circle.
sin (-100) = -0.985
Thus, in the unit circle the value of sin (100) = 0.985 and the value of sin (-100) = -0.985, in three decimal places.
Learn more about unit circle here: https://brainly.com/question/30403151
#SPJ1
Classify the polynomial by degree and number of terms: 3x ^ 4 - 3x ^ 2 - 7x
Cubic Binomial
Quintic Trinomial
Cubic Trinomial
Quartic Trinomial
Answers
The polynomial 3x^4 - 3x^2 - 7x is classified as a Cubic Trinomial.
The polynomial 3x^4 - 3x^2 - 7x can be classified as a Cubic Trinomial.
Here's the breakdown of the classification:
Degree: The highest power of the variable x is 4, so the degree of the polynomial is 4. Since the degree is 4, the polynomial is not cubic (which would have a degree of 3) or quintic (which would have a degree of 5).
Number of terms: The polynomial consists of three terms: 3x^4, -3x^2, and -7x. A polynomial with three terms is called a trinomial.
For more question on polynomial click on
https://brainly.com/question/2833285
#SPJ11
Answer:Quartic trinomial
Step-by-step explanation:
Don't listen to the other guy, I put cubic and I got the answer wrong thanks to the other guy.
An insurance provider states that their customers save at least, on average, 300 dollars per year by switching to them, with a standard deviation of 150 dollars. Before we decide to switch to the new company and go through all of the hassle, we want to test the claim. So, we go out and sample 64 individuals who switched to the new insurance company and found them to have saved an average of 255 dollars per year. Do we have enough evidence at the α = 0.05 level to state that the insurance provider is false in their claim? Discussion Prompts Answer the following questions in your initial post: What are the hypotheses based on the words given in the problem? Should we use a Z or T distribution in this case? What is our Z or T statistic? What is the P-value? Based on your p-value and alpha, what conclusion will we make? Based on your results, would you switch to this company? Explain why or why not (Note: this can go beyond the use of statistics, but statistical analysis can help our decisions)
Answers
The solution to the question is mathematically given as
1)
H0: M \(\geqslant\) 300
H0: M \(\geqslant\) 300
2)
Z distribution.
3)
z=-2.4
4)
P=0.0082
5)
"H0" is rejected as a hypothesis with a level of significance of 0.05.
What is the hypothesis ?Generally, the equation for is mathematically given as
Solutions
we have, \($u=300$$$\begin{aligned}& \sigma=150 \text { dollars } \\N &=64 \text { individuals } \\\bar{x} &=255 \text { dollare. } \\a=& 0.05 .\end{aligned}\)
(1):
H0: M \(\geqslant\) 300 dollars; customers save at least 300 dollars per year by switching to them.
H0: M \(\geqslant\) 300 dollars:
(This is a left-tailed test)
(2):
when \(\sigma\) is known, we use the Z test. we use Z distribution.
(3):
\(\begin{gathered}z=\frac{\bar{x}-\mu}{6 / \sqrt{n}}=\frac{255-300}{150 / \sqrt{64}}=\frac{-45}{18.75}=-2.4 \\z=-2.4\end{gathered}\)
(4):
\(Pvalue $=P(z < -2 \cdot 4)$ $=0.0082 \quad\{$ wing $z$ tables $\}$ \\\\\text { Pvalue }=0.0082\)
(5):
In conclusion, Since p-value = 0·0082 <0.05
This is statistically significant at the 0.05 level.
We thus "Refect H0" using a threshold of significance of 0.05.
"H0" is rejected as a hypothesis with a level of significance of 0.05.
There is not enough data to support the assertion that consumers may save at least $300 annually by switching insurance providers.
Therefore, we would not consider making the transition to this firm.
Read more about probability
https://brainly.com/question/795909
#SPJ1