Grayson is behind on his retirement savings and wants to start saving $1,000 per month so he can retire in 20 years. If he earns 9% a year, compounded monthly, how much money will Grayson have to retire? $622,447 $667,887 $684,254 $724,333
Answers
If Grayson begins saving $1,000 per month and makes 9% a year, compounded monthly, he will have $667,887 in retirement. Therefore, $667,887 is the correct number.
Future Value: What Is It?A financial notion known as future value (FV) gives a worth to an asset based on anticipated factors like future interest rates and cashflows. Knowing how much their money might be in five years, given an anticipated rate of return, may be helpful for an investor. Future value is the idea of taking the investment's current worth, adding anticipated development, and estimating what the investment is going to cost in the future.
To calculate the amount of money Grayson will have at retirement, we can use the formula for the future value of an annuity:
FV = Pmt x (((1 + r/n)^(n*t)) - 1) / (r/n)
where:
FV is the future value of the annuity (i.e., the amount Grayson will have at retirement)
Pmt is the monthly payment ($1,000 in this case)
r is the annual interest rate (9% in this case)
The number of annual increasing times is n. (12 for monthly compounding)
t is the number of years (20 in this case)
Plugging in the numbers, we get:
FV = 1000 x (((1 + 0.09/12)⁽¹²*²⁰⁾) - 1) / (0.09/12)
FV = $667,887.20
Therefore, Grayson will have $667,887 at retirement if he starts saving $1,000 per month and earns 9% a year, compounded monthly. Therefore, the answer is $667,887.
To know more about Future value visit:
https://brainly.com/question/29053212
#SPJ1
Related Questions
if the work required to stretch a spring 1 ft beyond its natural length is 6 ft-lb, how much work (in ft-lb) is needed to stretch it 6 in. beyond its natural length
Answers
According to the question The work needed to stretch the spring 6 in. beyond its natural length is 36 ft-lb.
If the work required to stretch a spring 1 ft beyond its natural length is 6 ft-lb, we can find the work needed to stretch it 6 in. beyond its natural length.
Let's denote the work required to stretch the spring by W. We can set up a proportion based on the lengths and work values:
\(\(\frac{1 \text{ ft}}{6 \text{ ft-lb}} = \frac{6 \text{ in.}}{W \text{ ft-lb}}\)\)
To find W, we can cross-multiply and solve for W:
1 ft × W ft-lb = 6 ft-lb × 6 in.
\(W = \(\frac{6 \text{ ft-lb} \times 6 \text{ in.}}{1 \text{ ft}}\)\)
W = 36 ft-lb
Therefore, the work needed to stretch the spring 6 in. beyond its natural length is 36 ft-lb.
To know more about spring visit -
brainly.com/question/29434686
#SPJ11
4
Type the correct answer in each box.
The area of a square is given by s2 and the perimeter is given by 4s, where s is the side length of the square.
If the side length of a square is 4 inches, Its area is
square inches and its perimeter is
inches.
Reset
Next
Answers
Answer:
Area = 16sq inches
Perimeter = 16 inches
Step-by-step explanation:
The shape of body is a square:
Area = S²
Perimeter = 4S
S is the side length
So;
S = 4inches
Therefore;
Area = S² = 4² = 16sq inches
Perimeter = 4S = 4(4) = 16inches
!No Links; Please
2x+3(x^2-10x-12)
find the product
Answers
Answer: 3x^2-28x-36
hope it helps :)
suppose that 78% of all dialysis patients will survive for at least 5 years. in a simple random sample of 100 new dialysis patients, what is the probability that the proportion surviving for at least five years will exceed 80%, rounded to 5 decimal places?
Answers
The probability that the 78% of all the dialysis patients survive for at least five years will exceed 80%, rounded to 5 decimal places is 0.3192.
What is the probability?The proportion of dialysis patients surviving for at least 5 years = 78% = 0.78
Assuming that a simple random sample of 100 dialysis patients is selected, the sample size is n = 100.
Let p be the proportion of dialysis patients in the sample surviving for at least 5 years.
Then, the sample mean is given by:
μp = E(p) = p = 0.78
So, the mean proportion of dialysis patients surviving for at least 5 years is equal to 0.78.
The standard error of the sample proportion is given by:
σp=√p(1−p)/n
σp=√0.78(1−0.78)/100
σp=0.04278
The required probability is to find P(p > 0.80):
P(p > 0.80) = P(Z > (0.80 - 0.78)/0.04278)
P(p > 0.80) = P(Z > 0.467) = 1 - P(Z < 0.467) = 1 - 0.6808 = 0.3192 (rounded to 5 decimal places)
Therefore, the probability that the proportion surviving for at least five years will exceed 80% in a simple random sample of 100 new dialysis patients is 0.3192.
Learn more about Probability here:
https://brainly.com/question/30034780
#SPJ11
How do you subtract mixed fractions with different denominators examples?
Answers
Answer: To subtract mixed fractions with different denominators, you need to convert the mixed fractions to equivalent fractions with a common denominator. Once the fractions have a common denominator, you can simply subtract the numerators and keep the denominator the same.
Example:
the difference of 2 1/3 and 1 3/4 is 5/12.
Step-by-step explanation:
First, convert 2 1/3 to an improper fraction: 2 1/3 = 7/3
Next, convert 1 3/4 to an improper fraction: 1 3/4 = 7/4
Now, both fractions have the same denominator, 3. So, you can subtract the numerators:
7/3 - 7/4 = (7 * 4 - 7 * 3) / (3 * 4) = 28/12 - 21/12 = 7/12
Finally, convert the answer back to a mixed fraction: 7/12 = 7 ÷ 12 = 5/12.
Jada earns $7 dollars per hour mowing her neighbors’ lawns. Name the two quantities in Jada’s situation that are in a functional relationship. Which did you choose to be the independent variable? What is the variable
Answers
The two quantities in Jada’s situation that are in a functional relationship are the number of hours she works (independent variable) and the amount of money she earns (dependent variable).
The two quantities in Jada’s situation that are in a functional relationship are the number of hours she works and the amount of money she earns. The number of hours worked is the independent variable because it is the variable that affects the amount of money earned. The amount of money earned is the dependent variable because this is the variable that is dependent on the number of hours worked.If she works 8 hours, she would earn $56.Jada earns $7 per hour, so if she works 3 hours, she would earn
$21 (3 x 7 = 21).
If she works 5 hours, she would earn
$35 (5 x 7 = 35).
If she works 8 hours, she would earn
$56 (8 x 7 = 56).
Learn more about independent variable here
https://brainly.com/question/29430246
#SPJ4
This past winter, 643 flamingos migrated to Gordon Lake. A researcher states that the number of flamingos migrating to the lake is decreasing by 12 birds every year. Which of the following represents the number of flamingos, n, that will migrate to the lake t winters from last winter if the researcher’s trend continues? A. t = 643 - 12n B. n = 643 - 12t C. t = 12 - 643n D. n = 12 - 643t
Answers
Answer:
n=643-12t
i had this question on an exam and got it right
Define Chi square test OR Tests of significance based on Chi-Square. A: -Various tests of significance described previously have mostly applicable to only quantitative data and usually to the data which are approximately normally distributed. It may also happens that we may have data which are not normally Inference: (i) If Z0 ≤ Ze we accept the H0 (ii) If Z0 >Ze we reject the H0 Example: A test of the breaking strengths of two different types of cables was conducted using samples of n1 = n2 = 100 pieces of each type of cable. Do the data provide sufficient evidence to indicate a difference between the mean breaking strengths of the two cables? Use 0.01 level of significance. x = 1925 and sigm = 40 and X2 = 1905, sigma = 30
Answers
The Chi-square test is a statistical test used to determine if there is a significant difference between observed and expected frequencies in categorical data. In this example, the test is used to assess whether there is a significant difference in the mean breaking strengths of two types of cables.
The Chi-square test of significance is employed when dealing with categorical or nominal data. It compares the observed frequencies with the frequencies that would be expected if the variables were independent. In this case, the breaking strengths of the two cables are the variables of interest.
To perform the test, the first step is to define the null hypothesis (H0) and the alternative hypothesis (Ha). In this example, H0 assumes that there is no difference in the mean breaking strengths of the two cables, while Ha suggests that there is a difference.
Next, the test statistic, denoted by X2 (chi-square), is calculated using the formula X2 = Σ[(O - E)²/E], where O represents the observed frequencies and E represents the expected frequencies under the assumption of independence.
To determine the expected frequencies, we need to estimate the means and variances of the breaking strengths. Here, x = 1925 and sigma = 40 for the first cable, and x = 1905 and sigma = 30 for the second cable.
Once the test statistic is calculated, it is compared to a critical value from the Chi-square distribution with degrees of freedom equal to (r - 1)(c - 1), where r is the number of rows and c is the number of columns in the contingency table. The significance level of 0.01 determines the critical value.
If the calculated X2 value is greater than the critical value, we reject the null hypothesis and conclude that there is sufficient evidence to indicate a difference in the mean breaking strengths of the two cables. Conversely, if the calculated X2 value is less than or equal to the critical value, we fail to reject the null hypothesis and conclude that there is no significant difference.
To learn more about chi-square click here: brainly.com/question/32379532
#SPJ11
2x +5y +1=0
3x + 7y= 1
Answers
Answer:
We can solve this system of equations using substitution or elimination.
Using substitution, we can solve for one variable in terms of the other in one equation and substitute that expression into the other equation. For example, we can solve the first equation for x in terms of y:
2x + 5y + 1 = 0
2x = -5y - 1
x = (-5/2)y - 1/2
Now we can substitute this expression for x into the second equation:
3x + 7y = 1
3((-5/2)y - 1/2) + 7y = 1
-15/2 y - 3/2 + 7y = 1
9.5y = 5
y = 5/9.5 = 1/1.9
Now we can substitute this value of y back into either equation to solve for x:
x = (-5/2)y - 1/2
x = (-5/2)(1/1.9) - 1/2
x = -2.632
So the solution to the system of equations is x = -2.632 and y = 1/1.9.
Complete the input-output table for the function f = 3 + n.
Input n 0 1 2 3
Output f 3
Answers
The complete table of values is
X |f(x)
0 | 3
1 | 4
2 | 5
3 | 6
How to complete the table of valuesFrom the question, we have the following parameters that can be used in our computation:
f = 3 + n
We have the x values to be
x = 1, 2 and 3
Substitute the known values in the above equation, so, we have the following representation
f = 3 + 1 =4
f = 3 + 2 = 5
f = 3 + 3 = 6
So, the values to use are 4, 5 and 6
Read more about functions at
brainly.com/question/28277110
#SPJ1
four times a # added to -7,
subtracted from twice the
Sum of four times the # and 6
simplify
Right answers only please
Answers
Answer:
4x + 19Step-by-step explanation:
Let the number be x
Four times a # added to -7:
4x + (-7) = 4x -7Sum of four times the # and 6:
4x + 6Subtracted from twice the Sum:
2(4x + 6) - (4x - 7) = 8x + 12 - 4x + 7 = 4x + 19Linda hears a story on National Public Radio stating that one in six eggs in the US are contaminated with Salmonella. If Salmonella contamination occurs independently within and between egg cartons and Linda makes a three-egg omelet, what is the probability that her omelet will contain at least one Salmonella-contaminated egg?
Answers
The probability that Linda's omelet will contain at least one Salmonella-contaminated egg is approximately 0.4213 or 42.13%.
We have,
To calculate the probability that Linda's omelet will contain at least one Salmonella-contaminated egg, we can use the concept of complementary probability.
The complementary event to "at least one Salmonella-contaminated egg" is "no Salmonella-contaminated eggs."
The probability of no Salmonella-contaminated eggs in a three-egg omelet is (5/6) x (5/6) x (5/6) since each egg has a 1/6 probability of not being contaminated.
Therefore,
The probability of at least one Salmonella-contaminated egg is:
= 1 - (5/6) x (5/6) x (5/6)
= 91/216 or approximately 0.4213.
Thus
The probability that Linda's omelet will contain at least one Salmonella-contaminated egg is approximately 0.4213 or 42.13%.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ4
Question 38.
Write the first six terms of the arithmetic sequence with the first term, a1 = 240, and common difference, d= 24.
The first six terms are a1 = ,a3= , a4= ,a5= , and a6= .
Answers
\(a(1) = 240 \\ a(2) = a(1) + d = 240 + 24 = 264 \\ a(3) = a(2) + d = 264 + 24 = 288 \\ a(4) = a(3) + d = 288 + 24 = 312 \\ a(5) = a(4) + d = 312 + 24 = 336 \\ a(6) = a(5) + d = 336 + 24 = 360\)
(x + yi) + (4 + 9i) = 9 - 4i
Answers
Answer:
x
=
5
−
y
i
−
13
i
Step-by-step explanation:
lost-time accidents occur in a company at a mean rate of 0.3 per day. what is the probability that the number of lost-time accidents occurring over a period of 7 days will be exactly 3? assume poisson situation. p(x
Answers
The probability that the number of lost-time accidents occurring over a period of 7 days will be exactly 3 is 0.7295
Binomial Distribution
The binomial distribution is the sum of a series of multiple independent and identically distributed Bernoulli trials. In a Bernoulli trial, the experiment is said to be random and can only have two possible outcomes- success or failure.
In a binomial distribution the probability of getting success must remain the same for the trials we are investigating. For example, when tossing a coin, the probability of flipping a coin is ½ or 0.5 for every trial we conduct, since there are only two possible outcomes.
Mean rate of lost time accident = 0.3 per day
probability that the number of lost-time accidents occurring over a period of 7 days will be no more than 3.
n = 7
Using binomial distribution formula :
P(x ≤3)
Probability of success (p) = 0.3
1 - p = 1- 0.3 = 0.7
nCx * p^x * (1 - p)^(n-x)
Using the binomial probability distribution calculator to save computation time :
P(x ≤3) = P(x = 0) + p(x = 1) + p(x = 2) + p(x = 3)
P(x ≤3) = 0.0403 + 0.1556 + 0.2668 + 0.2668
P(x ≤3) = 0.7295
0.7295
To learn more about Binomial distribution visit:
brainly.com/question/14565246
#SPJ4
Find the volume of the cone. Use 3.14 for pi
Round your answer to the nearest tenth if needed.
(Hint #1: the diagram displays the slanted height, NOT the vertical height).
(Hint #2: use properties of a 45-45-90 degree triangle to find the vertical height. Round this to the nearest tenth.)

Answers
Answer:
1329.3 yd³
Step-by-step explanation:
You want the volume of a cone with an offset peak such that the angle of elevation of the peak from one side of the base is 45°, and that slant height is 18 yards. The diameter of the base is 20 yards.
HeightThe ratio of sides in a 45°-45°-90° triangle is 1 : 1 : √2. That is, the height of the cone is ...
h = (18 yd)/√2 ≈ 12.7 yd . . . . . rounded height value
VolumeThe volume of the cone is given by ...
V = (π/3)r²h
The radius is half the diameter, so is ...
r = (20 yd)/2 = 10 yd
Then the volume is ...
V = (3.14/3)(10 yd)²(12.7 yd) ≈ 1329.3 yd³
The volume of the cone is about 1329.3 yd³.
__
Additional comment
If the "pi button" on the calculator is used, and no intermediate rounding of computation results is done, the volume is computed as 1332.9 yd³.
Loose granular material rarely has an angle of repose greater than 45°. The angle on the other side of the cone is about 60.3° relative to the base.
<95141404393>

Which expression is equivalent to
Please help I will mark brainlist !

Answers
Answer:
answer is b
Step-by-step explanation:
Please help me on 1,2, and 3 please help

Answers
Answer: put it in rice<333
Step-by-step explanation:
no matter what the resource allocation is, area a will always have the highest resource availability.
Answers
The given statement "no matter what the resource allocation is, area A will always have the highest resource availability," is not essentially true.
The term "area" generally refers to a specific region or part of a larger space. In the context of your question, area A represents a particular zone with resources allocated to it. Resource availability refers to the quantity and accessibility of resources in a given area.
To claim that area A will always have the highest resource availability regardless of resource allocation, it implies that there are factors inherent to area A that consistently make it the most resource-rich zone. This could be due to natural resource distribution, infrastructure, or other variables that ensure area A maintains the highest resource availability.
However, without additional information about area A and the specific resources in question, it is difficult to definitively state that area A will always have the highest resource availability.
To learn more about area visit : https://brainly.com/question/25292087
#SPJ11
.
Which of the following expressions is equivalent
31622
to
3/27 3/2
o 3.3.16
3/27.16
79. 19. 2
O
3
DONE
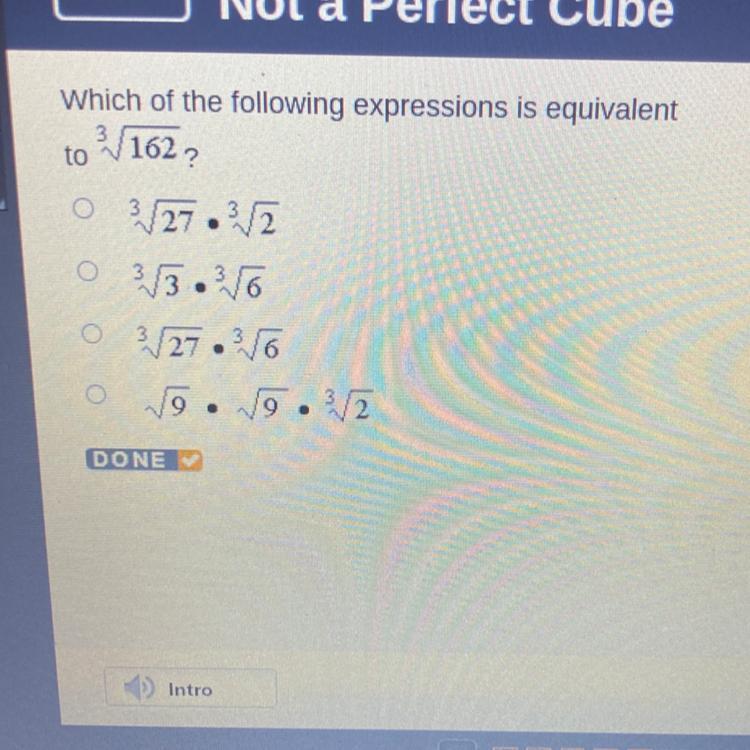
Answers
Answer:
a.18
b.162
c.9 3radical2
Find the solution of the following differential equation by Laplace transforms with initial conditions for each equation: a) y" – y = t y(0) = 1, y'(0) = 1 b) y" + y' = t² + 2t y(0) = 4, y'(0) = -2 c) d²y/dt⁴ + d³y/dt³ = cost y(0) = y'(0) = y"' (0) = 0, y" (0) = 1
Answers
Laplace transforms are an essential mathematical tool used to solve differential equations. These transforms transform differential equations to algebraic equations that can be solved easily.
To solve the differential equations given in the question, we will use Laplace transforms. So let's start:Solution:a) y" – y = t y(0) = 1, y'(0) = 1First, we take the Laplace transform of the given differential equation.L{y" - y} = L{ty}
Taking the Laplace transform of both sides gives:L{y"} - L{y} = L{ty}Using the formula, L{y"} = s²Y(s) - s*y(0) - y'(0), and L{y} = Y(s) then we get:s²Y(s) - s - 1 = (1/s²) + (1/s³)Rearranging the above equation, we get:Y(s) = [1/(s²*(s² + 1))] + [1/(s³*(s² + 1))]Now, we apply the inverse Laplace transform to find the solution.y(t) = (t/2)sin(t) + (cos(t)/2)
The solution of the differential equation y" – y = t, with initial conditions y(0) = 1, y'(0) = 1 is y(t) = (t/2)sin(t) + (cos(t)/2).
To know more about Laplace transforms visit
https://brainly.com/question/30759963
#SPJ11
plz help me. Solve this Question
Answer is 1. plz solve

Answers
Answer: \(m^{\frac{-bc^{2} + a^{2}b + ac^{2} - a^{3}}{a^{2}bc^{2}}\)
Classify these functions as even, odd, or neither
F(x) = 4x^3 - 3x^2 + 5
F(x) = -7x^2+1
y = cos (-x)
y = csc x
y = tan x / x
y = sin x/cos X
Pls help
Answers
Step-by-step explanation:
F(x) = 4x^3 - 3x^2 + 5 neither
F(x) = -7x^2+1 even
y = cos (-x) even
y = csc x odd
y = sin x/cos x odd
which sample size will produce the widest 95onfidence interval, given a sample proportion of 0.5?  a. 60  b. 80
Answers
For a given sample proportion of 0.5, the sample size that will produce the widest confidence interval is the largest option given, which in this case is 80.
The sample size that will produce the widest 95% confidence interval, given a sample proportion of 0.5, is option b, 80. This is because the width of the confidence interval is directly proportional to the sample size, meaning that as the sample size increases, the confidence interval becomes narrower.
Additionally, the width of the confidence interval is inversely proportional to the square root of the sample size. Therefore, for a given sample proportion of 0.5, the sample size that will produce the widest confidence interval is the largest option given, which in this case is 80.
Learn more about sample size here:
brainly.com/question/31734526
#SPJ11
Find the surface area of the prism

Answers
a building height has a height of 125 and a legth of 80 meters. On a scale drawing of the building, the height is 25 centimeters. what is the legth of the building on the scale drawing in centimeters
Answers
Answer: 16 cm
Step-by-step explanation:
Use ratios to solve:
125 m -> 25 cm
80 m -> x cm
Find the value of x:
x = 80*25/125 = 16
Hope this helps!
The length of the building on the scale drawing is 16 centimeters.
To determine the length of the building on the scale drawing in centimeters, we first need to establish the scale factor. Since the actual height of the building is 125 meters and its representation on the scale drawing is 25 centimeters, we can find the scale factor by dividing the height on the scale drawing by the actual height:
Scale factor = (Height on scale drawing) / (Actual height) = 25 cm / 125 m
As there are 100 centimeters in a meter, we need to convert the actual height to centimeters:
125 m * 100 = 12,500 cm
Now, we can recalculate the scale factor:
Scale factor = 25 cm / 12,500 cm = 1/500
This means that every 1 centimeter on the scale drawing represents 500 centimeters (or 5 meters) in reality. Now that we know the scale factor, we can use it to find the length of the building on the scale drawing:
Length on scale drawing = (Actual length) * (Scale factor) = 80 m * (1/500)
First, convert the actual length to centimeters:
80 m * 100 = 8,000 cm
Now, multiply by the scale factor:
Length on scale drawing = 8,000 cm * (1/500) = 16 cm
So, the length of the building on the scale drawing is 16 centimeters.
In summary, we can use the scale factor to convert between the actual measurements and the measurements on the scale drawing.
To know more about scale drawing, refer to the link below:
https://brainly.com/question/28651690#
#SPJ11
Henry runs each lap in 4 minutes. He will run at most 11 laps today. What are the possible numbers of minutes he will run today?
Answers
Answer:
44 Minutes
Step-by-step explanation:
If he takes for minutes per lap than some easy multiplication will do the job to find out how long 11 laps will take.
If he keeps running a lap in 4 minutes for every lap up, until the 11th lap, that means we multiply 11 times 4.
Another example being, if I run 1 lap in 1 minute then if I ran 2 laps it would take me 2 minutes, because 1 times 2 is 2, and so fourth for each lap. So if I ran 11 laps it would take me 11 minutes because 11 times 1 is 11.
Give The measures of the angle that is complementary to the given angle

Answers
Answer:
36°
Step-by-step explanation:
We know that
Sum of two complementary angles is 90°Let the other angle be xSo\( \rm \dashrightarrow \: x + 54 = 90 \\ \rm \dashrightarrow \: x = 90 - 54 \\ \rm \dashrightarrow \: x = 36\)
Solve and list your answer in interval notation. x+5 /X-3 ≤0
Answers
The solution to the inequality (x + 5) / (x - 3) ≤ 0 is an empty set. There are no values of x that satisfy the inequality. In interval notation, we represent this as an empty interval: ∅.
To solve the inequality (x + 5) / (x - 3) ≤ 0, we need to find the values of x that make the expression less than or equal to zero.
First, we identify the critical points where the expression becomes zero or undefined. In this case, the denominator x - 3 becomes zero at x = 3.
Next, we create a sign chart by testing intervals on the number line. We choose test points within each interval and determine the sign of the expression.
Test x = 0:
(0 + 5) / (0 - 3) = -5 / -3 = 5/3 > 0 (positive)
Test x = 4:
(4 + 5) / (4 - 3) = 9 / 1 = 9 > 0 (positive)
Test x = 10:
(10 + 5) / (10 - 3) = 15 / 7 > 0 (positive)
Based on the sign chart, the expression is positive (greater than zero) for all tested values of x. Therefore, the solution to the inequality (x + 5) / (x - 3) ≤ 0 is an empty set. There are no values of x that satisfy the inequality.
In interval notation, we represent this as an empty interval: ∅.
Learn more about interval from
https://brainly.com/question/30460486
#SPJ11
Seven friends are buying tickets to a concert. Each person pays $8. How much money do they pay altogether?
$
Answers
Answer:
56$
Step-by-step explanation:
8$x7=56.
you just need to multiply it