Graph this line using the slope and y-intercept: y= – 7x–3 Click to select points on the graph.
Answers
The slope of the line is -7 and the y-intercept is negative 3. The line is drawn below.
How to draw the graph of the function?The collection includes all locations on the surface of the shape (x, f(x)) that make up a function of f's graph. We may alternatively say that the graph of f is the curve of y = f. (x). As a result, the diagram of an equation is a particular instance of the graphs of functions.
A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
The linear equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
The equation is given below.
y = -7x - 3
More about the graph of the function link is given below.
https://brainly.com/question/27757761
#SPJ1

Related Questions
Simplity
-12c^8 divided by 6c^5
Answers
Answer:
-2c^13
hopefully i helped :)
Please look at the image and help me out (maths)
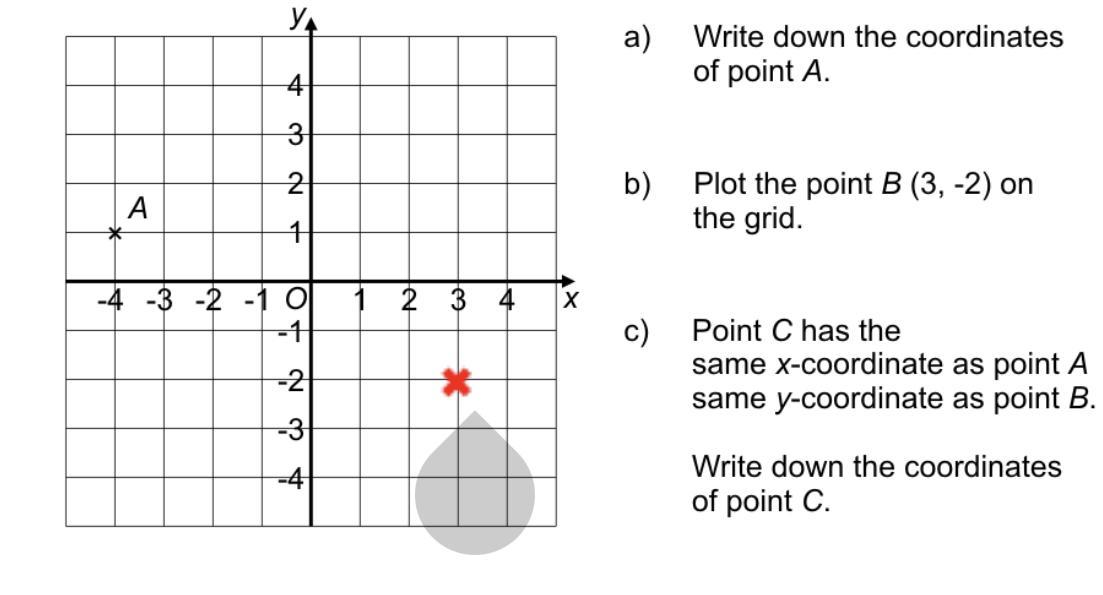
Answers
a) The coordinates of point A are given as follows: (-4,1).
b) The point B is plotted in red on the image given for this problem.
c) The coordinates of point C are given as follows: (-4,-2).
How to define the ordered pair?The general format of an ordered pair is given as follows:
(x,y).
In which the coordinates are given as follows:
x is the x-coordinate.y is the y-coordinate.Then the coordinates of point C are given as follows:
x = -4 -> same x-coordinate of point A.y = -2 -> same y-coordinate of point B.Hence the ordered pair is given as follows:
(-4, -2).
More can be learned about ordered pairs at brainly.com/question/1528681
#SPJ1
The population on a certain island increased from 1500 in 2000 to 1577 in 2001 a. Determine the growth rate b. Write a general equation for the popolation p(t) c. Estimate the population in 2010 d. How many years will it take for the population to double?
Answers
Therefore, it will take approximately 13.7 years for the population to double.
a. To determine the growth rate, you need to calculate the percentage increase in population. The formula for growth rate is:
Growth Rate = (New Value - Old Value) / Old Value * 100
Using the given values, we have:
Growth Rate = (1577 - 1500) / 1500 * 100
Growth Rate = 77 / 1500 * 100
Growth Rate ≈ 5.13%
b. To write a general equation for the population, you can use the formula:
p(t) = p(0) * (1 + r/100)^t
where p(t) is the population at time t, p(0) is the initial population, r is the growth rate, and t is the number of years.
c. To estimate the population in 2010, we need to find the population at time t = 2010 - 2000 = 10 years. Using the general equation from part b, and substituting the given values:
p(10) = 1500 * (1 + 5.13/100)^10
p(10) ≈ 1500 * (1.0513)^10
p(10) ≈ 1500 * 1.6436
p(10) ≈ 2465.4
Therefore, the estimated population in 2010 is approximately 2465.
d. To find out how many years it will take for the population to double, we need to solve the equation:
2 * p(0) = p(0) * (1 + r/100)^t
Simplifying the equation, we have:
2 = (1 + r/100)^t
Taking the logarithm of both sides, we get:
log(2) = t * log(1 + r/100)
Finally, solving for t, we have:
t = log(2) / log(1 + r/100)
Substituting the growth rate from part a, we have:
t = log(2) / log(1 + 5.13/100)
t ≈ log(2) / log(1.0513)
t ≈ 13.7 years
Therefore, it will take approximately 13.7 years for the population to double.
To know more about population visit :
https://brainly.com/question/19169926
#SPJ11
Let f be the function given by f(x) 9x. If four subintervals of equal length are used, what is the value of the right Riemann sum approximation for (x) dx?
Answers
The value of the right Riemann sum approximation for integral ∫₀² f(x) dx is (c) 60.
The right Riemann sum approximation is obtained by dividing the interval [0, 2] into four subintervals of equal length and evaluating the function at the right endpoints of each subinterval. In this case, each subinterval has a length of (2-0)/4 = 0.5. The right endpoints of the subintervals are 0.5, 1.0, 1.5, and 2.0.
To calculate the right Riemann sum, we evaluate the function at these right endpoints and sum up the values multiplied by the subinterval length.
f(0.5) = \(9^{0.5\) = 3
f(1) = 9¹ = 9
f(1.5) = \(9^{1.5\) = 27
f(2) = 9² = 27
The right Riemann sum is then
= (0.5 * f(0.5)) + (0.5 * f(1.0)) + (0.5 * f(1.5)) + (0.5 * f(2.0))
= 0.5 * (3 + 9 + 27 + 81)
= 60.
Therefore, the value of the right Riemann sum approximation for ∫2 to 0 f(x) dx is 60, which corresponds to option (c).
Learn more about Riemann sum here
https://brainly.com/question/30404402
#SPJ4
Given question is incomplete, the complete question is below
let f be the function given by f(x)= 9ˣ, if four subintervals of equal length are used, what is the value of the right riemann sum approximation for∫₀² f(x) dx. 20b. 40c. 60d. 80
Salton Sea Beach in California has an elevation of about −230 feet. This is about 11.5 times the elevation of Indio, California.
What is the elevation of Indio, California?
Answers
let indio, california's elevation be x
then salton sea beach elevation = 11.5 * x = -230
x = -230/11.5 = -20 feet
you're welcome....
find the postive value of x when y = 25
Answers
Heck I can't leave I should but I can't---At a local pet store, Shirley noticed that about four out of five customers who bought pets chose goldfish. Shirley wants to know the estimated probability that three randomly selected customers buying pets would not buy goldfish. How could Shirley design a simulation for this scenario?
A.
She could roll a six-sided die three times. On the die, numbers 1 to 3 represent customers who buy goldfish and 4 to 6 represent customers who don’t buy goldfish.
B.
She could spin a spinner divided into nine equal sections three times. On the spinner, four sections represent customers who buy goldfish and five sections represent customers who do not buy goldfish.
C.
She could spin a spinner divided into five equal sections three times. On the spinner, four sections represent customers who buy goldfish and one section represents customers who do not buy goldfish.
D.
She could use a random number generator to generate a set of three numbers from 0 to 9. The numbers 0 to 4 represent customers who buy goldfish, and 5 to 9 represent customers who do not buy goldfish.
E.
She could use a number generator to generate a set of five numbers from 0 to 3. The numbers 0 to 2 represent customers who buy goldfish, and 3 represents customers who do not buy goldfish.
Answers
Answer:
C. She could spin a spinner divided into five equal sections three times. On the spinner, four sections represent customers who buy goldfish and one section represents customers who do not buy goldfish.
Step-by-step explanation:
We are told that four out of five customers who bought pets chose goldfish.
Thus;
P(those who bought pets also chose gold fish) = 4/5
Therefore;
P(those who bought pets but do not buy gold fish) = 1 - (4/5) = 1/5
Now, she wants to know the estimated probability that three randomly selected customers buying pets would not buy goldfish.
The probability we have is 1/5.
Therefore,to accommodate the 3 randomly selected customers, we have to multiply the numerator and denominator for each probability by 3.
Thus;
P(those who bought pets also chose gold fish) = 4/5 × 3/3 = 12/15
P(those who bought pets but do not buy gold fish) = 1/5 × 3/3 = 3/15
Looking at the new probabilities, the simulation she can use is to divide a spinner into five equal sections three times so that for each section, we can have the probability of 1/5 and 4/5.
Thus, option C is correct.
Gianna invested $60,000 in an account paying an interest rate of 3.4% compounded
daily. Assuming no deposits or withdrawals are made, how much money, to the
nearest ten dollars, would be in the account after 11 years?
Answers
To the nearest ten dollars, there would be approximately $81,329 in the account after 11 years.
To calculate the future value of an investment with compound interest, we can use the formula:
FV = P(1 + r/n)^(nt)
Where:
FV = Future value
P = Principal amount (initial investment)
r = Annual interest rate (as a decimal)
n = Number of times interest is compounded per year
t = Number of years
In this case:
P = $60,000
r = 3.4% = 0.034 (as a decimal)
n = 365 (daily compounding)
t = 11 years
Plugging in these values, we can calculate the future value (FV):
FV = $60,000 * (1 + 0.034/365)^(365*11)
Calculating this expression, we find:
FV ≈ $60,000 * (1.000093835)^40015 ≈ $81,329.20
Therefore, to the nearest ten dollars, there would be approximately $81,329 in the account after 11 years.
For more such questions on dollars,click on
https://brainly.com/question/30057220
#SPJ8
a 17 feet ladder is placed against a building. the bottom of the ladder is sliding away from the building at a rate of 5 feet per second. find the rate at which the top of the ladder is slipping down at the instant when the bottom of the ladder is 15 feet from the base of the building.
Answers
The rate at which the top of the ladder is slipping down at the instant when the bottom of the ladder is 15 feet from the base of the building is -75/8 feet per second
The length of the ladder = 17
Consider the length of the base as x and the height is h
The rate at which the ladder is sliding = 5 feet per second
dx/dt = 5
Apply the Pythagorean theorem
x^2 + h^2 = 17^2
h^2 = 289 - x^2
h = \(\sqrt{289-x^2}\)
The rate of change of height with respect to x is
dh/dx = - x / (289 - x^2)^(1/2)
dh/dt = dh/dx × dx/dt
Substitute the values in the equation
= - 15 / (289 - 15^2)^(1/2) × 5
= -15/8 × 5
= -75/8 feet per second
Therefore, the rate of change of height when x = 15 is -75/8 feet per second
Learn more about rate of change here
brainly.com/question/29518179
#SPJ4
a random number generator picks a number from one to nine in a uniform manner. find mu
Answers
The expected value or mean μ of the random number generator is 5.
To find μ, the expected value or mean of the random number generator that picks a number uniformly from one to nine, we can use the formula for the mean of a discrete uniform distribution.
In a discrete uniform distribution, all outcomes have equal probabilities. Since the random number generator picks a number from one to nine uniformly, each number has a probability of 1/9.
The formula for the mean of a discrete uniform distribution is:
μ = (a + b) / 2
where a is the minimum value and b is the maximum value of the distribution.
In this case, a = 1 and b = 9. Substituting these values into the formula, we have:
μ = (1 + 9) / 2
= 10 / 2
= 5.
Therefore, the expected value or mean μ of the random number generator is 5.
Question: A random number generator picks a number from one to nine in a uniform manner. Then find the mean (\(\mu\)).
To know more about uniform distribution check the below link:
https://brainly.com/question/22209943
#SPJ4
To search for in-depth science content, visitAdult tickets to the fall play cost and student tickets cost . The drama class sold more student tickets than adult tickets to the fall play. If the class collected from ticket sales, how many student tickets were sold
Answers
If the class collected $660 from ticket sales, the drama class sold a total of 90 student tickets. Let's assume that the number of adult tickets sold is x.
Since the drama class sold 25 more student tickets than adult tickets, the number of student tickets sold can be expressed as (x + 25).
The total revenue from ticket sales is given as $660. Adult tickets cost $6 each and student tickets cost $3 each. Therefore, the total revenue can be expressed as 6x + 3(x + 25).
Setting up the equation: 6x + 3(x + 25) = 660.
Simplifying the equation: 6x + 3x + 75 = 660.
Combining like terms: 9x + 75 = 660.
Subtracting 75 from both sides: 9x = 585.
Dividing both sides by 9: x = 65.
Therefore, the drama class sold 65 adult tickets.
To find the number of student tickets sold, we substitute the value of x into the expression (x + 25): (65 + 25) = 90.
Thus, the drama class sold 90 student tickets.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
(2.3x10^4)x(1.5x10^-2
Answers
here's the solution luv

Answer:
3.45x10^2
Step-by-step explanation:
Thankyou
A segment is m units long. Find the distance between the midpoints of the first and last parts if the segment is divided into 5 equal parts.
Answers
The midpoints of the first and last parts are 4/5m units apart
How to determine the distance between the midpoints?The length of the line segment is given as
Length = m units
From the question, the number of partitions is given as
Partition = 5
So, the length of each partition is
Each partition = Length/Partition
This gives
Each partition = m/5
The midpoint of a partition is
Partition midpoint = m/5 x 1/2
Evaluate
Partition midpoint = m/10
The distance between the midpoints of the first and last segments is then calculated as
Distance = Length - 2 x Partition midpoint
So, we have
Distance = m - 2 x m/10
Evaluate
Distance = m - m/5
This gives
Distance = 4/5m
Hence, the distance is 4/5m units
Read more about midpoints at
https://brainly.com/question/24682065
#SPJ1
In football, a punter is the player that punts (kicks) the ball. The punter wants to maximize two things: the hangtime (the time the ball is in the area) and the range of the punt. We can treat the punt as a projectile. Image the punter is standing on the 50 yard line ( 1 yard =3 feet) and kicks the ball, giving it an initial velocity of 22.0 m/s at 50
∘
above the horizontal. You can assume the kick starts at ground level and air resistance is negligible. a.) (4 points) What are the x-and y-components of the initial velocity (in m/s) ? b.) (7 points) How long is the ball in the air from the time it is kicked until it hits the ground? c.) (4 points) Does the kick go into the endzone (50 yards away from the kick) or not? (You must show your work. Remember to make sure your units are correct.)
Answers
a) The x-component of the initial velocity is approximately 14.14 m/s, and the y-component is approximately 16.91 m/s.
b) The ball is in the air for approximately 3.44 seconds.
c) The kick does not reach the endzone (45.72 m) as the range of the kick is approximately 48.64 m.
a) To find the x- and y-components of the initial velocity, we can use trigonometry. The initial velocity is given as 22.0 m/s at an angle of 50 degrees above the horizontal.
The x-component of the initial velocity (Vx) can be calculated using:
Vx = V * cos(θ)
where V is the magnitude of the initial velocity and θ is the angle of the initial velocity.
Vx = 22.0 m/s * cos(50°) ≈ 14.14 m/s
The y-component of the initial velocity (Vy) can be calculated using:
Vy = V * sin(θ)
Vy = 22.0 m/s * sin(50°) ≈ 16.91 m/s
Therefore, the x-component of the initial velocity is approximately 14.14 m/s, and the y-component of the initial velocity is approximately 16.91 m/s.
b) The time the ball is in the air can be found using the y-component of the motion. The ball is kicked from ground level, so we can use the equation:
y = y0 + Vy * t - (1/2) * g * t^2
where y0 is the initial vertical position (0 m), Vy is the initial vertical velocity (-16.91 m/s), g is the acceleration due to gravity (-9.8 m/s^2), and t is the time.
Setting y equal to 0 and solving for t, we get:
0 = 0 + 16.91 * t - (1/2) * 9.8 * t^2
This is a quadratic equation, and solving it gives us two solutions: t = 0 and t ≈ 3.44 s. We discard the t = 0 solution as it represents the initial time.
Therefore, the ball is in the air for approximately 3.44 seconds.
c) To determine if the kick reaches the endzone (50 yards = 45.72 m away), we can calculate the horizontal distance traveled (range) using the x-component of the motion:
Range = Vx * t
Range = 14.14 m/s * 3.44 s ≈ 48.64 m
Since the range of the kick is less than the distance to the endzone (45.72 m), the kick does not reach the endzone.
To learn more about velocity visit : https://brainly.com/question/80295
#SPJ11
how do i simplify 6⁴ 6⁸ please help its dou today
Answers
Answer: 6^12 (or 2176782336)
When you multiply exponents with the same base, you add the exponents together. (e.g., x^m · x^n = x^m+n)
6^4 · 6^8 = 6^4+8 = 6^12
Find the product of 32 and 46. Now reverse the digits and find the product of 23 and 64. The products are the same!
Does this happen with any pair of two-digit numbers? Find two other pairs of two-digit numbers that have this property.
Is there a way to tell (without doing the arithmetic) if a given pair of two-digit numbers will have this property?
Answers
Let's calculate the products and check if they indeed have the same value:
Product of 32 and 46:
32 * 46 = 1,472
Reverse the digits of 23 and 64:
23 * 64 = 1,472
As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.
To find two other pairs of two-digit numbers that have this property, we can explore a few examples:
Product of 13 and 62:
13 * 62 = 806
Reversed digits: 31 * 26 = 806
Product of 17 and 83:
17 * 83 = 1,411
Reversed digits: 71 * 38 = 1,411
As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.
For example, let's consider the pair 25 and 79:
A = 2, B = 5, C = 7, D = 9
The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.
Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.
19. highlight where values show g(x) = 0 and what is the answer20. highlight where values show f(x) > g(x) and what is the answer

Answers
19) g(x)=0 is the value of x at points where the line cuts the x-axis
From the graph that is at:
x=-7, x=1, x=3, and x=9
20) f(x)>g(x) where the curve f(x) is higher than the curve g(x), and this is at:
x<-3, 07
6. Inverse distance weighting: What is it for? Why is it better than just an average? (5)
Answers
Inverse distance weighting is a useful tool for estimating values at unsampled locations in geostatistics. Another advantage of inverse distance weighting is that it allows for the incorporation of multiple variables into the estimation process.
Inverse distance weighting is a method used in geostatistics to estimate values at unsampled locations based on values at surrounding sample locations. It works by assigning weights to the sample points based on their proximity to the unsampled point. The closer a sample point is to the unsampled point, the higher its weight. The weights are then used to calculate a weighted average of the sample values, which is used as the estimate for the unsampled location.
The benefit of inverse distance weighting over a simple average is that it takes into account the spatial variability of the data. A simple average treats all sample points equally, regardless of their distance from the unsampled point. This can lead to inaccurate estimates if there is a high degree of spatial variability in the data. In contrast, inverse distance weighting gives more weight to sample points that are closer to the unsampled point, which is likely to provide a more accurate estimate.
Another advantage of inverse distance weighting is that it allows for the incorporation of multiple variables into the estimation process. For example, if there are two variables of interest (e.g., temperature and precipitation), inverse distance weighting can be used to estimate values for both variables simultaneously. This is not possible with a simple average.
Overall, inverse distance weighting is a useful tool for estimating values at unsampled locations in geostatistics. Its ability to account for spatial variability and incorporate multiple variables makes it a powerful technique for analyzing spatial data.
for more questions on variables
https://brainly.com/question/29058061
#SPJ11
a) Work out the value of x and give
a reason for your answer.
+
53°
+
Lo
b) Work out the value of y and give
a reason for your answer.
Circle theorems
Answers
The value of x and y from the given figure are 106 and 127 respectively.
Circle geometryFor a circle geometry, the sum of the opposite angles of the quadrilateral is 180 degrees. Hence;
53 + y = 180
y = 180 - 53
y = 127 degrees
Also, the angle at the center is twice that at the circumference. Hence:
x = 2(53)
x = 106 degrees
Hence the value of x and y from the given figure are 106 and 127 respectively.
Learn more on circle geometry here: https://brainly.com/question/24375372

what is the importance of federal system
Answers
Featured snippet from the web
It protects against tyranny. One reason for the creation of a federal system was to prevent any one part of the government from having too much power. By decentralizing power, our federal system helps to protect us from having one part of the government become too strong at which point it could tyrannize us.
Can you please solve this as soon as you can? Thank you!

Answers
Step-by-step explanation:
x=120⁰
hdbdbdddfhcydhgdjvds
Help will give brainliest
Using order of operations, which calculation should be done first to simplify this expression?
48 + 3 x (4 + 8) ÷ 4
4 + 8
4 + 8
48 + 3
48 + 3
8 ÷ 4
8 ÷ 4
3 x 4
Answers
Answer:
4+8
Step-by-step explanation:
oh and the answer to the whole equation is 153
Verify the distributive property: a x (b + c) = a x b + a x c where, a = −3/11 , b = 9/5 , c = 1/5
Answers
Answer:
Distributive property is verified.
Step-by-step explanation:
Verifying distributive property:
a * (b +c) = a*b + a*c
a = -3/11 ; b = 9/5 ; c = 1/5
LHS = a * (b + c)
First Slove that is inside the parenthesis, (b +c)
\(\sf = \dfrac{-3}{11}*\left(\dfrac{9}{5}+\dfrac{1}{5}\right)\\\\=\dfrac{-3}{11}*\dfrac{10}{5}\\\\= \dfrac{-3}{11}*2\\\\=\dfrac{-6}{11}\)
RHS = a * b + a*c
\(\sf = \dfrac{-3}{11}*\dfrac{9}{5} +\dfrac{-3}{11}*\dfrac{1}{5}\\\\=\dfrac{-27}{55}-\dfrac{3}{55}\\\\=\dfrac{-30}{55}\\\\=\dfrac{-30 \div 5}{55 \div 5}\\\\=\dfrac{-6}{11}\)
LHs = RHS
Hence, verified
Solve the equation below

Answers
Answer:
(-3,8)
Step-by-step explanation:
7x+5y=19
y=8
Because we know y=8 we cane use 8 instead of y in the first equation.
1) 7x+5(8)=19
2) 7x+40=19
3) 7x=-21
4) x=-3
Checking the work)
1) 7(-3)+5(8)=19
2) -21+40=19
3) 19=19
6 x 1000000000000000
Answers
Answer:
6000000000000000
Step-by-step explanation:
Answer:
6000000000000000
Step-by-step explanation:
add {-6 -2 2}+ {-3 2 1}
Answers
Answer:
\(\huge\boxed{\sf \left[\begin{array}{ccc}-9&0&3\end{array}\right] }\)
Step-by-step explanation:
\(\sf = \left[\begin{array}{ccc}-6&-2&2\end{array}\right] + \left[\begin{array}{ccc}-3&2&1\end{array}\right] \\\\= \left[\begin{array}{ccc}-6+(-3)&-2+2&2+1\end{array}\right] \\\\= \left[\begin{array}{ccc}-6-3&0&3\end{array}\right] \\\\= \left[\begin{array}{ccc}-9&0&3\end{array}\right] \\\\\rule[225]{225}{2}\)
Hope this helped!
~AH1807Peace!A computer processes tasks in the order they are received. Each task takes an Exponential amount of time with the average of 2 minutes. Compute the probability that a package of 5 tasks is processed in less than 8 minutes.
Answers
The probability that a package of 5 tasks is processed in less than 8 minutes is 0.963.
Let X denote the time required to process a package of five tasks. X is an exponentially distributed random variable with mean 2 minutes.
The probability of X being less than 8 minutes is given by:
P(X ≤ 8) = 1 - P(X > 8)
= \(1 - (1 - e^{(-8/2)}^{5}\)
= 0.963
Therefore, the probability that a package of 5 tasks is processed in less than 8 minutes is 0.963.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ4
Clark Heter is an industrial engineer at Lyons Products. He would like to determine whether there are more units produced on the night shift than on the day shift. The mean number of units produced by a sample of 82 day-shift workers was 359. The mean number of units produced by a sample of 88 night-shift workers was 365. Assume the population standard deviation of the number of units produced is 35 on the day shift and 42 on the night shift. At the 0.05 significance level, is the number of units produced on the night shift larger? a. Is this a one-tailed or a two-tailed test?
b. State the decision rule.
Answers
At the 0.05 significance level, is the number of units produced on the night shift larger. This is a two-tailed test.
The mean number of units produced by a sample of 82 day-shift workers was 359. The mean number of units produced by a sample of 88 night-shift workers was 365.
The population standard deviation of the number of units produced is 35 on the day shift and 42 on the night shift.
To determine whether there are more units produced on the night shift than on the day shift.
Null Hypothesis, H0: μ1 = μ2
Alternative Hypothesis, Ha: μ1 < μ2
Pooled Variance
\(sp = \sqrt{(S_1)^2/n_1+(S_2)^2/n_2}\)
sp = √(441/82 + 784/88)
sp = 3.77
Test statistic,
\(z = (\bar x_1 - \bar x_2)/sp\)
z = (359 - 365)/3.77
z = -1.59
P-value Approach
P-value = 0.0968
As P-value >= 0.05, fail to reject null hypothesis.
At the 0.05 significance level, is the number of units produced on the night shift larger. This is a two-tailed test.
Learn more about Hypothesis here:
https://brainly.com/question/17063554
#SPJ4
there are 650 students at Malcolm middle school. 40% of the students say they enjoy math class. how many students at Malcolm middle enjoy math class. SOMEONE ANSWER
Answers
260 Students enjoy math class.
say you randomly select americans until you find one who is married. how many americans would you expect to select in order to find your first married respondent? round to two decimal places.
Answers
On average, you would expect to select approximately 1.90
Americans in order to find your first married respondent. This is because according to the U.S. Census Bureau, the national marriage rate in 2018 was 6.9 per 1,000 individuals, which is equivalent to 0.69% of the population being married.
Therefore, if we assume the population of Americans is uniformly distributed, the probability of randomly selecting a married American is 0.69%. Consequently, the expected number of trials necessary to select a married respondent is 1/0.0069 = 1.90.
To calculate this, we used the probability formula for a single trial: P(X) = N/S, where P(X) is the probability of success, N is the number of successes, and S is the number of trials.
Therefore, by substituting the number of successes (1) and the probability of success (0.0069) into the formula, we can determine the expected number of trials necessary to select a married respondent (1/0.0069 = 1.90).
To know more about U.S. Census Bureau click on below link:
https://brainly.com/question/28341588#
#SPJ11