Given the function f(x, y) =-3x+4y on the convex region defined by R= {(x,y): 5x +2y < 40,2x + 6y < 42, x > 0, y>0} (a) Enter the maximum value of the function 38 (6) Enter the coordinates (x,y) of a point in R where f(x, y) has that maximum value.
Answers
The maximum value of the function f(x, y) = -3x + 4y on the convex region R is 28. This maximum value occurs at the point (0, 7), which is a corner point of the feasible region defined by the given constraints.
To compute the maximum value of the function f(x, y) = -3x + 4y on the given convex region R, we need to solve the linear programming problem.
The constraints for the linear programming problem are:
1. 5x + 2y < 40
2. 2x + 6y < 42
3. x > 0
4. y > 0
To determine the maximum value of the function, we can use the method of corner points. We evaluate the objective function at each corner point of the feasible region defined by the constraints.
The corner points of the region R are the points of intersection of the lines defined by the constraints. By solving the system of equations formed by the constraint equations, we can find the corner points.
The corner points of the region R are:
1. (0, 7)
2. (4, 3)
3. (10, 0)
Now we evaluate the objective function f(x, y) = -3x + 4y at each corner point:
1. f(0, 7) = -3(0) + 4(7) = 28
2. f(4, 3) = -3(4) + 4(3) = 0
3. f(10, 0) = -3(10) + 4(0) = -30
The maximum value of the function f(x, y) on the region R is 28, which occurs at the point (0, 7).
To know more about maximum value refer here:
https://brainly.com/question/22562190#
#SPJ11
Related Questions
Find anexpression for the sum of fourconsecutive odd integers.
Answers
Given:-
Sum of four consecutive odd integers.
To find the required expression.
So the first term is n.
So the second term is n+2.
So the third term is n+4.
So the fourth term is n+6.
So the sum of terms is,
\(n+(n+2)+(n+4)+(n+6)_{}\)Where n is an odd integer.
Michelle withdrew $120 from her bank
account. She now has $3345 in her
account. Write and solve an equation to
find how much money m was in her
account before she made the withdrawal
Answers
Answer:
3345+120=3465
Step-by-step explanation:
Nalini thinks of an number. She doubles it and adds 5. Her answer is sixteen more than the number she thought. What number did Nalini think of? a) 10 b) 11 c)12 d) 6
Answers
x = 11
She thought of 11
Answer:
B. 11
Step-by-step explanation:
We can try it for each
10*2+5=25
25-10=15❌
11*2+5=27
27-11=16 ✔
12*2+5=29
29-12=17❌
6*2+5=17
16-6=11❌
So it's B
Solve the following quadratic function
by utilizing the square root method.
y = 16 – x2
Answers
. Assume that the annual percentage rate increases by 5%, 10%, 20%, 40%, and 60%. [30 marks] a. Calculate the approximate doubling time (Dappx) b. Calculate the exact doubling time (Dexact) c. Calculate the percentage error in calculating the doubling time for each case.
Answers
a) Approximate Doubling Time Dappx = 70/r, where r is the annual interest rate in percentage terms.Assuming that r = 5%, 10%, 20%, 40%, and 60%Doubling time for 5% = 70/5 = 14 yearsDoubling time for 10% = 70/10 = 7 yearsDoubling time for 20% = 70/20 = 3.5 yearsDoubling time for 40% = 70/40 = 1.75 yearsDoubling time for 60% = 70/60 = 1.1667 yearsb) Exact Doubling Time Dexact = ln2/r where r is the annual interest rate in decimal terms.
Assuming that r = 5%, 10%, 20%, 40%, and 60%For 5%: ln2/0.05 ≈ 13.86 yearsFor 10%: ln2/0.1 ≈ 6.93 yearsFor 20%: ln2/0.2 ≈ 3.47 yearsFor 40%: ln2/0.4 ≈ 1.73 yearsFor 60%: ln2/0.6 ≈ 1.16 yearsc)
The percentage error is given by:(Dexact − Dappx)/Dexact × 100%For 5%: (13.86 - 14)/13.86 x 100% ≈ 1.18%For 10%: (6.93 - 7)/6.93 x 100%
≈ 1.15%For 20%: (3.47 - 3.5)/3.47 x 100%
≈ -0.86%For 40%: (1.73 - 1.75)/1.73 x 100%
≈ -1.15%For 60%: (1.16 - 1.1667)/1.16 x 100%
≈ -0.60%Note that the percentage error is small for lower values of interest rates but increases as the interest rate increases.
Also, the percentage error is negative for 20%, 40%, and 60%, which means that the approximate doubling time is actually larger than the exact doubling time.
To know more about Doubling visit:
https://brainly.com/question/23848329
#SPJ11
2. {At the grocery store, Marilyn bought 4 apples and 7 oranges. Select two ways she could write the ratio of apples to oranges.} {3. There are 12 inches in 1 foot. How many inches are in 12 feet?} {4. Alexa is making a bracelet using beads. She uses 1 red bead for every 5 silver beads. If she uses a total of 20 silver beads, how many red beads does she use?}* {5. Peter is assembling gift bags for his birthday party. For every two Hershey candy cars he puts in each bag, he puts 3 lollipops. He decides to put six Hershey candy cars in one bag. How many lollipops does he put in the same bag?} Whoever can answer these questions you are amazing!!! And I give you 50 points =D
Answers
Answer:
I'm really sorry I wish I could give you the right answer but maybe if you like put it in like different parts cause it's like I can't read it to sa jumbled up but I will answer you if you put it in different parts please
Which triangle pairs are similar polygons?
Answers
Triangle pairs are similar polygons if they have the same shape but not necessarily the same size. In order for two triangles to be similar, they must satisfy the following conditions:
They must have the same angles. This means that the measures of the angles in one triangle must be the same as the measures of the corresponding angles in the other triangle.
The lengths of the sides must be in the same ratio. This means that if you divide the lengths of the corresponding sides of one triangle by the lengths of the corresponding sides of the other triangle, you must get the same ratio for all pairs of sides.
For example, if triangle ABC is similar to triangle DEF, the ratios of AB/DE, AC/DF, and BC/EF must all be the same.
To determine if two triangles are similar, you can use one of several theorems and postulates, such as the Side-Side-Side (SSS) Similarity Theorem, the Side-Angle-Side (SAS) Similarity Theorem, or the Angle-Angle (AA) Similarity Postulate. These theorems and postulates provide different sets of conditions that must be satisfied in order for two triangles to be similar.
To more about triangle similarity follow link : https://brainly.com/question/8691470
#SPJ4
Aaron has 47 m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. (The fourth side of the enclosure would be the river.) The area of the land is 266 square meters. List each set of possible dimensions (length and width) of the field.
Answers
The possible dimensions (length and width) of the field are:(10 m × 13 m) or (13 m × 10 m) and (11 m × 12 m) or (12 m × 11 m).
Given that Aaron has 47m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. The fourth side of the enclosure would be the river.
The area of the land is 266 square meters.To find the possible dimensions (length and width) of the field, we can use the given information.The length of fencing required = 47 m.
Since the fence needs to be built on three sides of the rectangular plot, the total length of the sides would be 2l + w = 47.1. When l = 10 and w = 13, we have:
Length of the field, l = 10 m Width of the field, w = 13 mArea of the field = l × w = 10 × 13 = 130 sq. m2. When l = 11 and w = 12,
we have:Length of the field, l = 11 m
Width of the field, w = 12 m
Area of the field = l × w = 11 × 12 = 132 sq. m
To learn more about : dimensions
https://brainly.com/question/28107004
#SPJ8
a system of equations is shown.
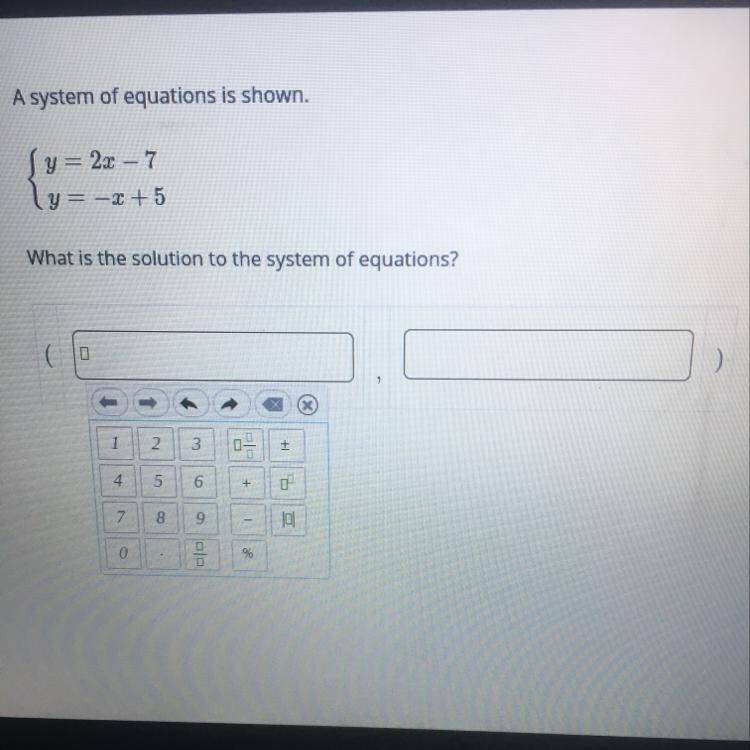
Answers
Answer:
x=4 , y=1
Step-by-step explanation:
y = 2x-7
y = -x +5
Set them equal to each other
2x-7 = -x+5
add x to each side
2x+x-7 = -x+x+5
3x-7 = 5
Add 7 to each side
3x-7+7 = 5+7
3x = 12
Divide by 3
3x/3 = 12/3
x=4
Now find y
y = -x+5
y = -4 +5
y = 1
The Andromeda galaxy is 2.54 million (2.54x106) light years from earth. If light can travel 5.865 trillion (5.865x1012) miles in a
year then how many miles is the Andromeda galaxy from earth?
O 1.48971x1019
O 2.309055x106
3.325x106
O 8.405x1018
Answers
Answer: 1.48971 x 10^19
Step-by-step explanation: 1-light year is approximately 5.865 x 10^12 which is 5,865,000,000,000 kilometers or 6 trillion miles in 1-year. The Andromeda galaxy is indeed 2.54 million light-years from Earth which is the closest galaxy to our Milky Way Galaxy.
The best way to this is to put this into a scientific calculator. If it shows 1.48971E19, the E stands for exponent and the 19 next to the E stands to the 19th power. That is written as 1,489,710,000,000,000,000 miles!! from Earth. That's a lot of zeros. That's the reason scientific notation is used; to avoid all those zeros and express very small/large figures.
Hope this explanation helps.
please help- What is the value of X ?

Answers
Answer:
\( x=12\sqrt 2\)
x = 100
Step-by-step explanation:
\( \sin \: 45 \degree = \frac{12}{x} \\ \\ \frac{1}{ \sqrt{2} } = \frac{12}{x} \\ \\ \huge \red{ x = 12 \sqrt{2} } \\ \\ \\ \sin \: 45 \degree = \frac{x}{100 \sqrt{2} } \\ \\ \frac{1}{ \sqrt{2} } = \frac{x}{100 \sqrt{2} } \\ \\ x = \frac{100 \sqrt{2} }{ \sqrt{2} } \\ \\ \huge \purple{ x = 100 } \)
Which of the following factors does NOT control the stability of a slope?
the angle of repose for intact bedrock
whether the slope is rock or soil
the amount of water in the soil
the orientation of fractures, cleavage, and bedding
Answers
The factor that does NOT control the stability of a slope is the angle of repose for intact bedrock. The angle of repose refers to the steepest angle at which a pile of loose material remains stable without sliding. It is mainly applicable to loose materials like soil and granular substances, not intact bedrock.
Bedrock stability depends on factors such as its strength, fracturing, and geological properties, rather than the angle of repose. Factors that control the stability of a slope include whether the slope is rock or soil. Rock slopes tend to be more stable than soil slopes due to the cohesive nature of intact rock.
The amount of water in the soil also affects slope stability, as excessive water can increase pore pressure and reduce the shear strength of the soil, leading to slope failure. Additionally, the orientation of fractures, cleavage, and bedding in the rock can influence slope stability by creating planes of weakness or strength.
To summarize, while the angle of repose is a significant factor in slope stability, it is not applicable to intact bedrock. The stability of a slope is influenced by the type of material (rock or soil), the presence of water, and the orientation of fractures and bedding.
know more about Bedrock.
https://brainly.com/question/2948854
#SPJ11
please help me!!!!!

Answers
Answer: 194
Step-by-step explanation:
1. Square both sides to get (b+2)=14^2=196
2. Subtract 2 from both sides to get b=194
Breast-feeding mothers secrete calcium into their milk. Some of the calcium may come from their bones, so mothers may lose bone mineral. Researchers measured the percent change in mineral content of the spines of 47 mothers during three months of breast-feeding.6Here are the data:
Blend Images/Superstock
(a)
The researchers are willing to consider these 47 women as an SRS from the population of all nursing mothers. Suppose that the percent change in this population has standard deviation ? = 2.5%. Make a stemplot of the data to verify that the data follow a Normal distribution quite closely. (Don
Answers
To create a stemplot, we first need to separate the data into "stems" and "leaves." Each stem represents the first digit(s) of each data point, while each leaf represents the last digit(s). For example, if the data point is 12.3, the stem would be 12 and the leaf would be 3.
To make a stemplot, the data should be arranged in increasing order, and then separated into stems and leaves.
STEMPLOT OF THE DATAHowever, you can use the data given and arrange it in increasing order and separate it into stems and leaves to make a stemplot. A stemplot is a good way to check if the data follow a normal distribution quite closely, the more the data is spread out and the more symmetric it is, the more likely it is to follow a normal distribution.
Also, it is important to mention that from the given data, it is not possible to conclude if the percent change in this population has standard deviation of 2.5%. This parameter can only be estimated from a sample if it follows a normal distribution which is not clear from the given data.
Learn more about Stemplot here:
https://brainly.com/question/29174445
#SPJ4
formula of (a^3+b^3)
Answers
Answer:
\((a+b)(a^2-ab+b^2)=(a^3+b^3)\)
Step-by-step explanation:
What’s the difference between 25,770 97,355
Answers
Which expression has the greatest value?
16
V162
✓642
84

Answers
given the relation R = {P, Q, R, S, T, U, V, W, X, Y, Z} and the set of functional dependencies F = { {P, R}→{Q}, {P}→{S, T}, {R}→{U}, {U}→{V, W}, {S}→{X, Y}, {U}→{Z}}. Find the key for R? Decompose R into 2NF and then 3NF relations and then to BCNF (show the steps of decomposition steps clearly).
Answers
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
R4({S, X, Y}, {P → R4}) or ({R → R4})
To find the key for R, we need to determine which attribute(s) uniquely identify each tuple in R. We can do this by computing the closure of each attribute set using the given functional dependencies F.
Starting with P, we have {P}+ = {P, R, U, V, W, Z}, since we can derive all other attributes using the given functional dependencies. Similarly, {R}+ = {R, U, V, W, Z}. Therefore, both {P} and {R} are candidate keys for R.
To decompose R into 2NF, we need to identify any partial dependencies in the functional dependencies F. A partial dependency exists when a non-prime attribute depends on only a part of a candidate key. In this case, we can see that {P}→{S, T} is a partial dependency since S and T depend only on P but not on the entire candidate key {P,R}.
To remove the partial dependency, we can create a new relation with schema {P, S, T} and a foreign key referencing R. This preserves the functional dependency {P}→{S,T} while eliminating the partial dependency.
The resulting relations are:
R1({P, R, Q, U, V, W, Z})
R2({P, S, T}, {R → R2})
To decompose R into 3NF, we need to identify any transitive dependencies in the functional dependencies F. A transitive dependency exists when a non-prime attribute depends on another non-prime attribute through a prime attribute.
In this case, we can see that {U}→{V,W} is a transitive dependency since V and W depend on U through the prime attribute R. To eliminate this transitive dependency, we can create a new relation with schema {U, V, W} and a foreign key referencing R.
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
To decompose R into BCNF, we need to identify any non-trivial functional dependencies where the determinant is not a superkey. In this case, we can see that {S}→{X,Y} is such a dependency since S is not a superkey.
To remove this dependency, we can create a new relation with schema {S, X, Y} and a foreign key referencing P (or R). This preserves the functional dependency while ensuring that every determinant is a superkey.
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
R4({S, X, Y}, {P → R4}) or ({R → R4})
Learn more about resulting from
https://brainly.com/question/1578168
#SPJ11
PLEASE HELP, I'M RUNNING OUT OF TIME


Answers
The equation of the line is y = 0.4x - 793.65 and the minimum wage is $18.35
What is Equation of LineThe equation of a line can be formed with the help of the slope of the line and a point on the line. Let us understand more about the slope of the line and the needed point on the line, to better understand the formation of the equation of a line. The slope of the line is the inclination of the line with the positive x-axis and is expressed as a numeric integer, fraction, or the tangent of the angle it makes with the positive x-axis. The point refers to a point in the coordinate system with the x coordinate and the y coordinate.
a)
Taking two points from the table;
Using 1996 and 1997
The data are; (1996, 4.75), (1997, 5.15)
m = y₂ - y₁ / x₂ - x₁
m = 5.15 - 4.75 / 1997 - 1996
m = 0.4
The slope of the line is 0.4
Using the line equation;
y = mx + c
Taking one point, we can find y-intercept here
5.15 = 0.4(1997) + c
5.15 = 798.8 + c
c = 5.15 - 798.8
c = -793.65
The equation of the line is y = 0.4x - 793.65
b) The minimum wage in 2030
y = 0.4x - 793.65
y = 0.4(2030) - 793.65
y = 18.35
The minimum wage is $18.35
Learn more on equation of line here;
https://brainly.com/question/18831322
#SPJ1
Sixty-four percent of voters in a very large electorate support candidate Smith in an upcoming election. A student employee working the evening shift at a telephone survey facility calls voters at random and asks them which candidate they prefer. a. What is the probability that, among five voters the student calls, exactly one supports candidate Smith? b. What is the probability that, among five voters the student calls, at least one supports candidate Smith? c. What is the probability that the first voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach the first voter who supports candidate Smith? d. What is the probability that the third voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach three voters who supports candidate Smith?
Answers
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4
\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5
\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls. The calculation results in approximately 0.369, or 36.9%.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
[P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
[P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
PLEASE HELP ITSS TIMED!!!
Choose any 3 of the 4 features listed below for the function log2(x-3)+5 and include a description of how you found those answers using complete sentences.
1) Vertical Asymptote: (Name the equation of the asymptote and tell me how you found it from the equation or where you found it on the graph.)
2) X and Y Intercepts: (Name the x and y intercepts and tell me how you found them from the equation or where you found them on the graph.)
3) Transformations compared to its parent function LaTeX: f\left(x\right)=\log_2x\:. (You can just list the specific tranformations that occurred such as vertical shifts, horizontal shifts, stretch or compress, any reflections)
4) Domain: (Name the domain of this function and tell me how you found it from the equation or where you found it on the graph.)
Answers
A store sells a 1 1/4 pound package of turkey for $9
.What is the unit price of the turkey in the package?
Answers
If 1(1/4) pound of turkey is sold for $9, then the unit-price of the turkey is $7.20 per pound.
The "Unit-Price" is defined as the price of a single unit or item of a product, typically expressed in terms of a standard unit of measurement, such as price per pound, price per liter, or price per piece.
To find the unit price of turkey in the package, we need to divide the total cost of the package by the weight of the turkey in the package.
First, we need to convert 1(1/4) pounds to a decimal, which is 1.25 pounds.
Then, we can find the unit price by dividing the total-cost of $9 by the weight of the turkey in the package:
⇒ Unit price = (Total cost)/(Weight of turkey in package),
⇒ Unit price = $9/1.25 pounds,
⇒ Unit price = $7.20 per pound,
Therefore, the unit price of turkey in the package is $7.20 per pound.
Learn more about Unit Price here
https://brainly.com/question/29023044
#SPJ1
The given question is incomplete, the complete question is
A store sells a 1(1/4) pound package of turkey for $9. What is the unit price of the turkey in the package?
What is this number in standard form?
(8×10)+(2×1100)+(9×11,000)
Enter your answer in the box.
Answers
Answer:
101280 is the answer
Step-by-step explanation:
Consider a continuous-time Markov chain with three states 1, 2, 3, 4, 5 and transition rates q12=1, q13 = 2, q21 = 0, q23 = 3, q31 = 0, q32 = 0. (1) Write the system of ODEs for the corresponding transition probabilities Pᵢⱼ (t) . (2) Suppose that the initial state is 1. What is the probability that after the first transition, the process X(t) enters state 2?
Answers
the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
To write the system of ordinary differential equations (ODEs) for the transition probabilities Pᵢⱼ(t) of the given continuous-time Markov chain, we need to consider the rate at which the system transitions between different states.
Let Pᵢⱼ(t) represent the probability that the Markov chain is in state j at time t, given that it started in state i at time 0.
The ODEs for the transition probabilities can be written as follows:
dP₁₂(t)/dt = q₁₂ * P₁(t) - q₂₁ * P₂(t)
dP₁₃(t)/dt = q₁₃ * P₁(t) - q₃₁ * P₃(t)
dP₂₁(t)/dt = q₂₁ * P₂(t) - q₁₂ * P₁(t)
dP₂₃(t)/dt = q₂₃ * P₂(t) - q₃₂ * P₃(t)
dP₃₁(t)/dt = q₃₁ * P₃(t) - q₁₃ * P₁(t)
dP₃₂(t)/dt = q₃₂ * P₃(t) - q₂₃ * P₂(t)
where P₁(t), P₂(t), and P₃(t) represent the probabilities of being in states 1, 2, and 3 at time t, respectively.
Now, let's consider the second part of the question: Suppose that the initial state is 1. We want to find the probability that after the first transition, the process X(t) enters state 2.
To calculate this probability, we need to find the transition rate from state 1 to state 2 (q₁₂) and normalize it by the total rate of leaving state 1.
The total rate of leaving state 1 can be calculated as the sum of the rates to transition from state 1 to other states:
total_rate = q₁₂ + q₁₃
Therefore, the probability of transitioning from state 1 to state 2 after the first transition can be calculated as:
P(X(t) enters state 2 after the first transition | X(0) = 1) = q₁₂ / total_rate
In this case, the transition rate q₁₂ is 1, and the total rate q₁₂ + q₁₃ is 1 + 2 = 3.
Therefore, the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
Learn more about probability here
https://brainly.com/question/32117953
#SPJ4
You take a package to the local shipping company. They charge a fixed base cost of $3 per package plus an additional $0. 63 per pound. If P represents the number of pounds of your package, and C is the total cost of shipping your package, write an equation that represents the relationship between P and C
Answers
If P represents the number of pounds of your package, and C is the total cost of shipping your package, the equation that represents the relationship between P and C is C = 3 + 0.63P.
To write an equation that represents the relationship between the weight of the package (P) and the total cost of shipping (C), we need to use the information given in the problem. The shipping company charges a fixed base cost of $3 per package plus an additional $0.63 per pound.
We can represent the additional cost per pound as 0.63P, since the cost increases by $0.63 for every additional pound. Therefore, the equation that represents the relationship between P and C is:
C = 3 + 0.63P
This equation gives us the total cost of shipping a package based on its weight. We can use this equation to calculate the cost of shipping a package of any weight by simply plugging in the weight (in pounds) for P and then solving for C.
For example, if a package weighs 5 pounds, we can substitute P = 5 into the equation to get:
C = 3 + 0.63(5)
C = 3 + 3.15
C = 6.15
To learn more about equation click on,
https://brainly.com/question/30391353
#SPJ4
What topics are introduced in Algebra 2?
Answers
Answer:
Algebra 2 typically builds on the concepts covered in Algebra 1 and introduces more advanced topics such as:
Quadratic equations and functions
Complex numbers
Polynomial functions and their operations
Rational functions and their operations
Conic sections
Exponential and logarithmic functions
Sequences and series
Trigonometry
Matrices and determinants
Permutations and combinations
Probability
Functions and relations
Limits and derivatives
Answer:
rrtgf thing for them code mine took also
3
Step-by-step explanation:
tutfd
what must be true for any direction if the instantaneous rate of change from (1,3,2) is equal to 0? what shape is formed by the collection of these vectors? (be as specific as you can.)
Answers
The instantaneous rate of change is the change in the rate at a particular instant and it is same as the change in derivative value at a specific point.
From the above given data, the following solution is given below:
Given:
Let f(x,y,z) = x³z - yz²
To find the partial derivatives of f
Here the directional derivative of a function f(x,y,z) is given by:
(df/dx , df/dy, df/dz)
df/dx = 3x²
df/dy = -z²
df/dz = x³ - 2yz
at points(1,3,2)
(df/dx)₍₁,₃,₂₎ = 3(1)² = 3
| (df/dx)₍₁,₃,₂₎ | = 3
(df/dy)₍₁,₃,₂₎ = -2² = 4
| (df/dy)₍₁,₃,₂₎ | = 4
(df/dz)₍₁,₃,₂₎ = 1³ - 2*3*2 = 1-12 = -11
| (df/dz)₍₁,₃,₂₎ | = 11
As we got the maximum modulus of derivative in direction of x. Since, therefore we should move into z direction to maximize the directional derivative.
(df/dz)₍₁,₃,₂₎ = -11
Hence, the instantaneous rate of change is the change in the rate at a particular instant and it is same as the change in derivative value at a specific point.
To know more about derivative check the below link:
https://brainly.com/question/28376218
#SPJ4
The instantaneous rate of change is the change in the rate at a particular instant and it is same as the change in derivative value at a specific point | (∂f/∂z)₍₁,₃,₂₎ | = 11.
What is instantaneous rate of change?
The derivative value change at a particular point is the same as the instantaneous rate of change, which is the change in rate at a specific instant. The tangent line slope and the instantaneous rate of change at a given point on a graph are the same. That is, the slope is curved.
From the given data, the solution is given below:
Given:
Let f(x, y, z) = x³z - yz²
To find the partial derivatives of f
Here the directional derivative of a function f(x, y, z) is given by:
(∂f/∂x , ∂f/∂y, ∂f/∂z)
∂f/∂x = 3x²
∂f/∂y = -z²
∂f/∂z = x³ - 2yz
at points(1,3,2)
(∂f/∂x)₍₁,₃,₂₎ = 3(1)² = 3
| (∂f/∂x)₍₁,₃,₂₎ | = 3
(∂f/∂y)₍₁,₃,₂₎ = -2² = 4
| (∂f/∂y)₍₁,₃,₂₎ | = 4
(∂f/∂z)₍₁,₃,₂₎ = 1³ - 2*3*2 = 1-12 = -11
| (∂f/∂z)₍₁,₃,₂₎ | = 11
As we got the maximum modulus of derivative in direction of z. Since, therefore we should move into z direction to maximize the directional derivative.
(∂f/∂z)₍₁,₃,₂₎ = -11
Hence, The instantaneous rate of change is the change in the rate at a particular instant and it is same as the change in derivative value at a specific point.
To know more about instantaneous rate of change, click on the link
https://brainly.com/question/24592593
#SPJ4
Complete question:
Complete question is attached below.


Please help me..................................................................................


Answers
Answer:
The given image is a graph of an exponential function. The graph is in the form of y = ab^x, where a is the initial value (y-intercept), b is the base (growth or decay factor), and x is the exponent (input value).
In this particular graph, the function appears to be a decay function since the value of the function is decreasing as x increases. We can also see that the initial value of the function is 24, which means that when x = 0, y = 24. We can also see that the base of the function is less than 1 (approximately 0.8), which tells us that the function is decreasing at a constant rate.
To write the exponential function that represents this graph, we can use the general form of the function y = ab^x and substitute the known values:
y = 24(0.8)^x
Therefore, the exponential function that represents the given graph is y = 24(0.8)^x.
Image 2.
The given image is a graph of an exponential function. The graph is in the form of y = ab^x, where a is the initial value (y-intercept), b is the base (growth or decay factor), and x is the exponent (input value).
In this particular graph, the function appears to be a growth function since the value of the function is increasing as x increases. We can also see that the initial value of the function is 5, which means that when x = 0, y = 5. We can also see that the base of the function is greater than 1 (approximately 1.2), which tells us that the function is increasing at a constant rate.
To write the exponential function that represents this graph, we can use the general form of the function y = ab^x and substitute the known values:
y = 5(1.2)^x
Therefore, the exponential function that represents the given graph is y = 5(1.2)^x.
What is the equation of the line that passes through the points (-2,10) and (-9,-5)? Write your answer in slope intercept form
Answers
\((\stackrel{x_1}{-2}~,~\stackrel{y_1}{10})\qquad (\stackrel{x_2}{-9}~,~\stackrel{y_2}{-5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-5}-\stackrel{y1}{10}}}{\underset{run} {\underset{x_2}{-9}-\underset{x_1}{(-2)}}} \implies \cfrac{-15}{-9 +2} \implies \cfrac{ -15 }{ -7 } \implies \cfrac{ 15 }{ 7 }\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{10}=\stackrel{m}{ \cfrac{ 15 }{ 7 }}(x-\stackrel{x_1}{(-2)}) \implies y -10 = \cfrac{ 15 }{ 7 } ( x +2) \\\\\\ y-10=\cfrac{ 15 }{ 7 }x+\cfrac{ 30 }{ 7 }\implies y=\cfrac{ 15 }{ 7 }x+\cfrac{ 30 }{ 7 }+10\implies {\Large \begin{array}{llll} y=\cfrac{ 15 }{ 7 }x+\cfrac{100}{7} \end{array}}\)
And 7/8 hours Greg reads 2/3 chapters what’s the unit rate in chapters per hour?
Answers
The unit rate in chapters per hour is 21/16 hours
How to calculate the unit rate?Greg read 7/8 hours in 2/3 chapter
The unit rate can be calculated as follows
7/8= 2/3
1= x
cross multiply both sides
2/3x= 7/8
x= 7/8 ÷ 2/3
x= 7/8 × 3/2
x= 21/16
Hence 21/16 chapters is read in one hour
Read more on unit rate here
https://brainly.com/question/29216013
#SPJ1