Given the check digit is 3, find the missing number X for the Mater card number 5164 2X13 2705 0183?
SHOW WORK . please help!
Answers
Answer:
9
Step-by-step explanation:
So there's 3 1's, 2 2's, 2 3's, 1 4, 2 5's, a 6, a 7, an 8, 2 0's, and no 9's.
Related Questions
HELP ASAP.....NO LINKS AND NO TROLLING
the graph of f(x)=x^2 is shown
compare the graph of f(x) with the graph of g(x)=x^2+8

Answers
Convert g(x) to vertex form
y=x²+8y=(x-0)²+8Vertex at (0,8)
f(x) has vertex (0,0)Hence
f(x) is translated 8 units upOption D
Answer:
D. The graph of g(x) is 8 units above the graph of f(x)
Step-by-step explanation:
Transformations
For \(a > 0\)
\(f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}\)
\(f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}\)
\(f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}\)
\(f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}\)
Parent function: \(f(x)=x^2\)
Translated 8 units up: \(f(x)+8=x^2+8\)
Therefore, the graph of g(x) is 8 units above the graph of f(x)

the number which best completes the sequence below is: 20 5 30 6 42 7 ?
Answers
The answer to the question is 56. The sequence appears to alternate between adding and multiplying by a certain equation number.
From 20 to 5, we multiplied by 0.25 (or divided by 4). From 5 to 30, we added 25. From 30 to 6, we multiplied by 0.2 (or divided by 5). From 6 to 42, we added 36. Therefore, to continue the pattern, we need to multiply 7 by a certain number and then add another number. It turns out that if we multiply 7 by 8, we get 56. Adding 49 to 56 gives us the next number in the sequence: 105.
So, the long answer is that the number which best completes the sequence is 56, and the next number in the sequence after that would be 105. The sequence can be split into two sub-sequences: 20, 30, 42 and 5, 6, 7. The first sub-sequence represents an increasing series of even numbers (20, 30, 42) with a difference of 10, 12, and so on. The second sub-sequence represents a consecutive series of odd numbers (5, 6, 7). Combining these sub-sequences forms the original sequence.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ11
find u · v, v · v, ||u||² , (u · v)v, and u · (5v). u = (−3, 2), v = (4, 3)
a. u · v
b. v · v
c. ||u||²
d. (u · v)v
Answers
a) u · v, is -34 + 23 = -12 + 6 = -6. b) v · v, is 44 + 33 = 16 + 9 = 25.
c) The squared norm of vector u, ||u||², is (-3)² + 2² = 9 + 4 = 13.
d) the dot product of u and v with v. In this case, (-6)(4, 3) = (-24, -18).
In the first paragraph, the dot product of vectors u and v is calculated by multiplying the corresponding components of the vectors and summing them. For u · v, (-34) + (23) = -12 + 6 = -6.
In the second paragraph, the other calculations are performed. For v · v, (44) + (33) = 16 + 9 = 25. The squared norm of vector u, ||u||², is found by squaring each component of u and summing them. (-3)² + 2² = 9 + 4 = 13. Finally, the expression (u · v)v represents the projection of vector u onto vector v and is obtained by multiplying the dot product of u and v with v. (-6)(4, 3) = (-24, -18).
Learn more about vectors here:
https://brainly.com/question/24256726
#SPJ11
HELP ASAP! Will name brainliest!

Answers
Answer:
The answer to your question is given in the attached photo.
Step-by-step explanation:
To determine the answer to the question,
First, we shall determine the value 3A.
This is obtained by multiplying matrix A by 3 as shown in the attached photo.
Next, we shall carry out the operation 3A – B as shown in the attached photo.

2. An article in the Journal of the American Medical Association reports the results of a
study designed to see if the herb St. John's wort is effective in treating moderately
severe cases of depression. The study involved 338 patients who were being treated
for major depression. The subjects were randomly assigned to receive one of three
treatments: St. John's wort, Zoloft (a prescription drug), or placebo (an inactive
treatment) for an 8-week period. The two way table summarizes the data from the
experiment
Treatment
a. What proportion of subjects in the study were
St. John's
randomly assigned to take St. John's wort?
wort Zoloft Placebo
Explain why this value makes sense.
Full
27 27
The proportion of subjects in the study that were randomly assigned
response
to take St. John's wort is about 1/3 (113/338).
Change in Partial
16 26 13
depression response
No
70 56 66
b. Find the distribution of change in depression
response
for the subjects in this study using relative
frequencies.
37
1
C. What percent of subjects took Zoloft and showed a full response?

Answers
Answer:
a. 113/338
b. The relative frequency distribution is presented as follows;
\({}\) St. John's wort Zoloft Placebo
Full response \({}\) 27/91 27/91 37/91
Partial response \({}\) 16/55 26/55 13/55
No response \({}\) 35/96 7/24 11/32
c. 29.67%
Step-by-step explanation:
a. The proportion of subjects assigned to take St. John wort is found as follows;
The total number of subjects = 27 + 27 + 37 + 16 + 26 + 13 + 70 + 56 + 66 = 338 subjects
The number of subjects assigned to take St. John wort = 27 + 16 + 70 = 113
The proportion of subjects assigned to take St. John wort = 113/338
b. The distribution of change in depression response using relative frequency is found as follows;
Total full response = 27 + 27 + 37 = 91
Total partial response = 16 + 26 + 13 = 55
No response = 70 + 56 + 66 = 192
\({}\) St. John's wort Zoloft Placebo
Full response \({}\) 27/91 27/91 37/91
Partial response \({}\) 16/55 26/55 13/55
No response \({}\) 35/96 7/24 11/32
c. The percentage of subjects that took Zoloft and showed full response is given as follows;
The percentage of subjects that took Zoloft and showed full response = 27/91 × 100 = 29.67%
WILL GIVE BRAINLIEST! (Geometry)
The circle below has a radius of 10 inches. Find the area of Sector A and Sector C
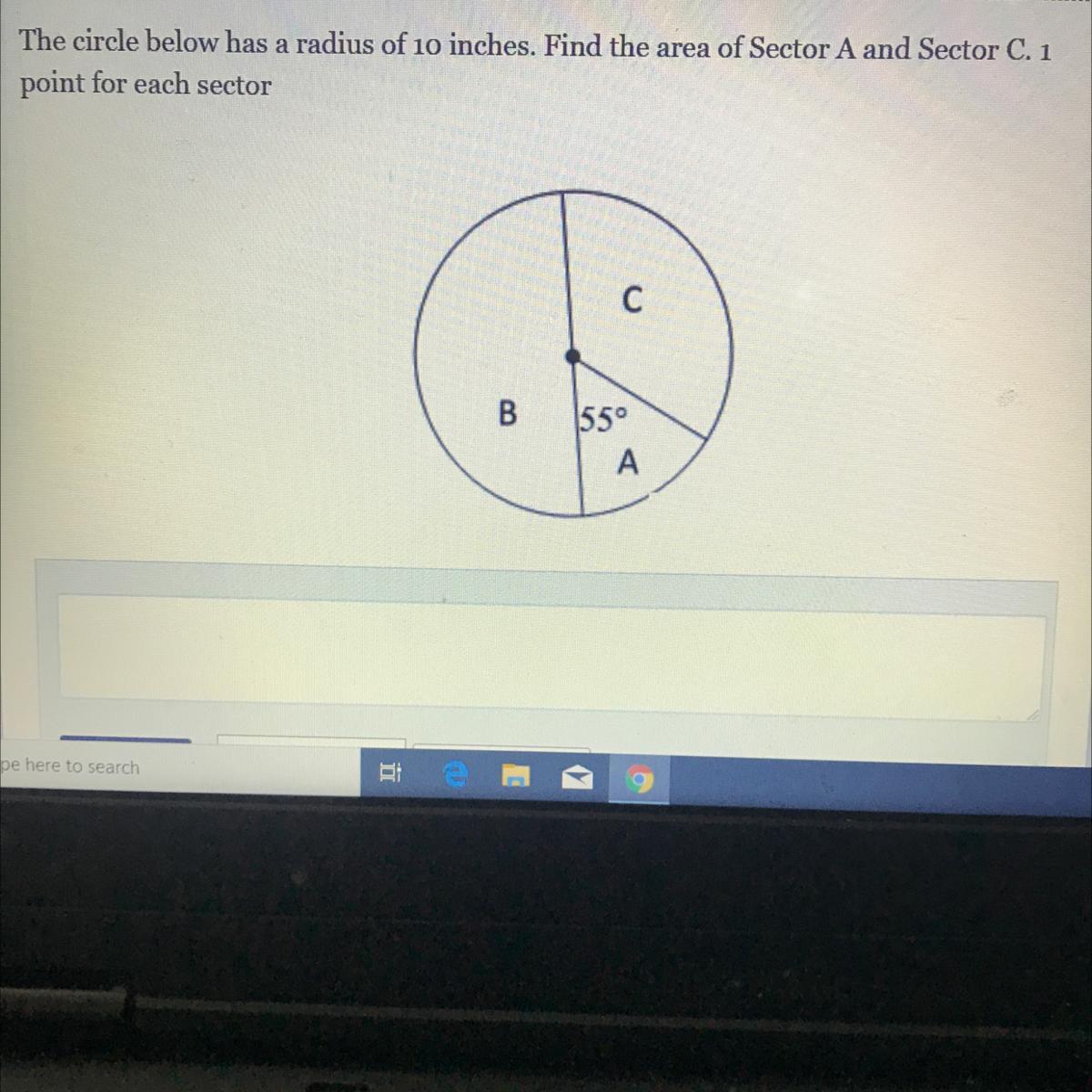
Answers
Answer:
area of sector A = 47.97 in²
area of sector C = 109.03 in²
Step-by-step explanation:
area of full circle = πr² = (3.14)(10²) = 314 in²
area of sector A = (55/360)(314) = 47.97 in²
area of sector C = (314/2) - 47.97 = 109.03 in²
Which value(s) is a solution for the inequality f < 4? Choose all that apply.

Answers
f = -4
f = 3
f = -2
Explanations:f < 4 means that f consists of all the values that are less than 4.
From the options:
Numbers that are less than 4 are -4, 3 and -2.
7 is greater than 4, therefore, f = 7 is an incorrect choice
(4.2x10^6)(1.1x10^7)
Answers
Answer:4.62x10^13
Step-by-step explanation:
What does * mean in mathematics?
Answers
Answer:
multiply
Step-by-step explanation:
for example:
4 * 5 = 20
other ways of writing multiply:
4 x 5 = 20
4(5) = 20
Answer:
Usually in math it is used to indicate multiplication.
Step-by-step explanation:
Most of the time people will use * instead of x for multiplication on a calculator or computer.
Hope this helps. Plz give brainliest.
.A ball that is dropped from a window hits the ground in 7 seconds. How high is the window? (Give your answer in feet; note that the acceleration due to gravity is 32 ft/s² . Height = _______
Answers
Answer:
(1/2)(32 ft/sec^2)((7 sec)^2)
= (16 ft/sec^2)(49 sec^2)
= 784 feet
Height = 112 feet.
To find the height of the window, we can use the following kinematic equation for motion with constant acceleration:
y = yo + voyt + ½at²
Here, y is the final height of the ball above the ground, yo is the initial height of the ball (which is the height of the window in this case), voy is the initial velocity of the ball (which is 0 because the ball is dropped from rest), t is the time taken for the ball to hit the ground (which is 7 seconds), and a is the acceleration due to gravity (which is 32 ft/s²).
Substituting the values, we have:y = yo + 0 + ½(32)(7)
Simplifying the expression, we get:y = yo + 112
Thus, the height of the window (in feet) is given by:y = 112 feet
Answer: Height = 112 feet
To know more about kinematic equations visit:
https://brainly.in/question/10166787
#SPJ11
Let X
t
be an AR(2) process defined by X
t
−X
t−1
+0.5X
t−2
=e
t
, where e
t
is a white noise innovation process with variance V(e
t
)=4. Find the covariance function of X
t
at lags zero, one and two, that is, compute r
X
(0),r
X
(1) and r
X
(2). Hint: Use the Yule-Walker equations.
Answers
The Yule-Walker equations relate the autocovariance function of a stationary time series to its autocorrelation function. In this case, we are interested in finding the autocovariance function.
The Yule-Walker equations for an AR(2) process can be written as follows:
r_X(0) = Var(X_t) = σ^2
r_X(1) = ρ_X(1) * σ^2
r_X(2) = ρ_X(2) * σ^2 + ρ_X(1) * r_X(1)
Here, r_X(k) represents the autocovariance at lag k, ρ_X(k) represents the autocorrelation at lag k, and σ^2 is the variance of the white noise innovation process e_t.
In our case, we are given that V(e_t) = 4, so σ^2 = 4. Now we need to find the autocorrelations ρ_X(1) and ρ_X(2) to compute the autocovariances.
Since X_t is an AR(2) process, we can rewrite the Yule-Walker equations in terms of the AR parameters as follows:
1 = φ_1 + φ_2
0.5 = φ_1 * φ_2 + ρ_X(1) * φ_2
0 = φ_2 * ρ_X(1) + ρ_X(2)
Solving these equations will give us the values of ρ_X(1) and ρ_X(2), which we can then use to compute the autocovariances r_X(0), r_X(1), and r_X(2).
To learn more about variance : brainly.com/question/31432390
#SPJ11
a recipe needs 1/4 tablespoon salt. this same recipe is made 5 time,es how much total is needed?
Answers
Answer:
1 and 1/4
Step-by-step explanation:
If you multiply 1/4 five times, you will get your answer
Ellora wants to accumulate $150000.00 in an RRSP by making annual contributions of $5000.00 at the beginning of each year. If interest is 5.5% compounded quarterly, calculate how long she has to make contributions.
a. 18.202125
b. 18.676765
c. 17.455483
d. 17.585794
e. 18.076686
Answers
Option A is the correct answer. Ellora wants to accumulate 150,000 in an RRSP by making annual contributions of 5,000 at the beginning of each year. If interest is 5.5% compounded quarterly, calculate how long she has to make contributions.
First, we have to find the interest rate per quarter, which will be
\(5.5% / 4\)= 1.375%.
The formula for the future value of an annuity is:
\(FV = (C * [(1 + r)^n - 1] / r)\),
For Ellora, \(FV = $150,000, C = $5,000, and r = 1.375%.\)
Substituting these values into the formula gives:
\(150,000 = 5,000 * [(1 + 0.01375)^n - 1] / 0.01375\)
Simplifying this equation gives:
\(30 = [(1.01375)^n - 1]\)
We can solve this using logarithms:
\(ln 30 = ln [(1.01375)^n - 1]\)
\(ln 30 = n * ln 1.01375 - ln 1.01375e^(ln 30) / e^(-ln 1.01375) = n18.202125 = n\)
Therefore, it will take Ellora 18.202125 years to accumulate 150,000 in her RRSP through \($5,000\)annual contributions made at the beginning of each year with interest of \(5.5%\) compounded quarterly.
To know more about compounded quarterly visit:-
https://brainly.com/question/29021564
#SPJ11
Question
Which polygon appears to be regular?
Responses
Figure A
Figure B
Figure C
Figure D

Answers
The answer would be figure B. (pentagon)

Calculate the rate of change for each given function.

Answers
Answer:
For function B the rise/run or the rate of change is 3/5 and for the chart would be 2
Step-by-step explanation:
Explain because its change in y/ change in x so up 3 over 5 would give 3/5 and for the chart is 2 because its change in y over change in x and since y is 4 and x is 2 4/2=2. hope this helps
Express (root 19 - root 7)(root 19 + root 7) in simplest form.
Answers
Answer
root 354
Step-by-step explanation:
Answer:
12
Step-by-step explanation:
(√19 -√7)(√19 +√7)
( a +b)( a -b) = a²-b²
(√19)² -(√7)² = 19 -7 = 12
Sussman Industries purchased a drilling machine for $100,000 and paid cash. Sussman expects to use the machine for 20 years, after which it will have no value. It will be depreciated straight-line over the 20 years. Assume a tax rate of 37%. What are the cash flows associated with the machine? Round the answers to the nearest whole dollar. Show inflows as positives and outflows as negatives (using the sign "-").
a. what is the amount at the time of purchase
b. What is the amount In each of the following 20 years
Answers
The cash flows for the depreciation per year for the 20 years are estimated.
a. Amount at the time of purchase is $-100,000 (Negative because it is an outflow)
b. Amount in each of the following 20 years:
The straight-line depreciation rate can be calculated by dividing the purchase price by the number of years the asset is expected to last.
Here, the purchase price is $100,000 and the expected life is 20 years.
Depreciation per year = Purchase price / Expected life
= $100,000 / 20
= $5,000 per year (constant for 20 years)
For each of the 20 years, the cash flows are as follows:
Year 1: -$5,000 (depreciation expense)
Year 2: -$5,000 (depreciation expense)
Year 3: -$5,000 (depreciation expense)
Year 4: -$5,000 (depreciation expense)
Year 5: -$5,000 (depreciation expense)
Year 6: -$5,000 (depreciation expense)
Year 7: -$5,000 (depreciation expense)
Year 8: -$5,000 (depreciation expense)
Year 9: -$5,000 (depreciation expense)
Year 10: -$5,000 (depreciation expense)
Year 11: -$5,000 (depreciation expense)
Year 12: -$5,000 (depreciation expense)
Year 13: -$5,000 (depreciation expense)
Year 14: -$5,000 (depreciation expense)
Year 15: -$5,000 (depreciation expense)
Year 16: -$5,000 (depreciation expense
)Year 17: -$5,000 (depreciation expense)
Year 18: -$5,000 (depreciation expense)
Year 19: -$5,000 (depreciation expense)
Year 20: -$5,000 (depreciation expense)
Know more about the Depreciation
https://brainly.com/question/27971176
#SPJ11
a researcher separated the people in a population into three political categories: democrat, republican, or independent. she then selected a random sample from each of these three groups. what kind of sample did she select?
Answers
The researcher makes use of stratified sampling method to select a random sample from each of the three groups mentioned.
It is given to us that -
A researcher separated the people in a population into three political categories:
Democrat
Republican
or, Independent.
It is also mentioned that she then selected a random sample from each of these three groups.
We have to determine the kind of sample she selected.
In this case, stratified sampling is used by the researcher to select a random sample.
Stratified sampling is a type of probability sampling method where the total population is segmented into homogenous groups to successfully complete the sampling technique.
Here we see that the researcher has separated the total population into homogenous groups of democrat, republican, or independent.
From these homogenous groups, she selected random samples.
Thus, the kind of sample selected by the researcher is stratified sampling.
To learn more about stratified sampling visit https://brainly.com/question/20544692
#SPJ4
Which set of decimals below is ordered from greatest to least?
A
0.4, 0.03, 0.2
B
0.72, 0.79, 0.80
C
0.78, 0.68, 0.7
D
0.8, 0.75, 0.09
Answers
0.78 0.68, 0.7
An equilateral triangle has a perimeter of 12x+33. What is the length of each side of the triangle?
Answers
The length of each side of the triangle is 3 2/3 units
What is an equilateral triangle?An equilateral triangle can be defined as a type of triangle having all three sides of equal length.
It is also known as a regular triangle.
Unlike other triangles, an equilateral triangle is one having not only two sides equal like an isosceles triangle but all of its sides equal in length.
The formula for perimeter of an equilateral triangle is expressed as;
P = 3x
Where;
P is the perimeterx is the length of its sideSubstitute the values
12x + 33 = 3x
collect like terms
12x - 3x = 33
substract the like terms
9x = 33
Make 'x' the subject
x = 33/9
x = 3 2/3 units
Hence, the value is 3 2/3 units
Learn more about equilateral triangles here:
https://brainly.com/question/17264112
#SPJ1
The National Junior Honor Society made $238at their cake sale. They sold circular Shaped cakes for $7 and heart shaped cakes for $5. If they Sold twice as many heart cakes as circular ones. how many heart cakes did they sell?
Answers
The number of heart cakes that were sold at the cake sale was 28
According to the question,
Cost of circular-shaped cake = $7
Cost of heart shaped cake = $5
Total sale = $238
Let the number of circular cakes shaped be x
Since the number of heart cakes was sold twice as many as the circular cake, the number of heart cakes will be 2x
Cost of x circular-shaped cake = $7 * x
Cost of 2x heart shaped cake = $5 * 2x
Total sale = Cost of x circular cake + Cost of 2x heart cake
Thus, we get the following equation,
238 = 7x + 10x
238 = 17x
x = 14
Thus, the number of heart cakes sold was 2x that is 28.
Learn more about Equation:
https://brainly.com/question/28871326
#SPJ1
24.7% of the products in the local shop are specialty soaps. 76% of those soaps are made with fresh herbs. if there are 350 bars of specialty soap in the shop, approximately how many of them are not made with fresh herbs? round your answer up to nearest whole number
Answers
we know that 76% of the specialty soaps are made with fresh herbs, and we also know that there are a total of 350 specialty soap bars, so how many are made with fresh herbs? well, just 76% of those 350
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{76\% of 350}}{\left( \cfrac{76}{100} \right)350}\implies 266\)
which ordered pair is a solution to the system of inequalities? y>3x y HELP WILL MARK BRAINLIEST

Answers
Answer:
D
Step-by-step explanation:
used guess-and-check and (1,5) is the only ordered pair that made each inequality true
Simplify the expression (d^7)^6
Answers
Answer:
d^42
Step-by-step explanation:
Hope this helps!
HELP I WILL GIVEBRAINLIST! FALSE ANSWERS OR SPAM WILL BE REPORTED!!!!1
What do the differences between the points (as shown on the graph) represent? On a coordinate plane, point B is at (2, 7) and point D is at (4, 14). StartFraction 7 over 2 EndFraction is the unit rate because it compares the change in y-values to the change in x-values of the points on the graph. StartFraction 2 over 7 EndFraction is the unit rate because it compares the change in y-values to the change in x-values of the points on the graph. StartFraction 7 over 2 EndFraction can be used to find the unit rate if one divides 7 by 2 and compares the result to 1. StartFraction 2 over 7 EndFraction can be used to find the unit rate if one divides 2 by 7 and compares the result to 1.
Answers
Answer:
StartFraction 7 over 2 EndFraction can be used to find the unit rate if one divides 7 by 2 and compares the result to 1
Step-by-step explanation:
we know that
The formula to calculate the slope between two points is equal to
we have the points
B(2, 7) and D(4, 14)
substitute the values
The unit rate is
therefore
StartFraction 7 over 2 EndFraction can be used to find the unit rate if one divides 7 by 2 and compares the result to 1
Step-by-step explanation:
Answer:
StartFraction 7 over 2 EndFraction can be used to find the unit rate if one divides 7 by 2 and compares the result to 1
Step-by-step explanation:
we know that
The formula to calculate the slope between two points is equal to
we have the points
B(2, 7) and D(4, 14)
substitute the values
The unit rate is
therefore
StartFraction 7 over 2 EndFraction can be used to find the unit rate if one divides 7 by 2 and compares the result to 1
find the standard equation of the sphere. (let r = 8 and c = (9, 2, 5).)
Answers
The standard equation of the sphere is:
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
The standard equation of a sphere is given by:
(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2
where (a, b, c) is the center of the sphere and r is the radius.
In this case, the center of the sphere is given by c = (9, 2, 5) and the radius is r = 8.
Substituting these values into the standard equation of the sphere, we get:
(x - 9)^2 + (y - 2)^2 + (z - 5)^2 = 8^2
Expanding and simplifying, we get:
x^2 - 18x + 81 + y^2 - 4y + 4 + z^2 - 10z + 25 = 64
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
Therefore, the standard equation of the sphere is:
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
To know more about standard equation refer here :
https://brainly.com/question/29059560#
#SPJ11
the kutta-joukowski theorem, equation (3.140), was derived exactly for the case of the lifting cylinder. in section 3.16 it is stated without proof that equation (3.140) also applies in general to a two-dimensional body of arbitrary shape. although this general result can be proven mathematically, it also can be accepted by making a physical argument as well. make this physical argument by drawing a closed curve around the body where the closed curve is very far away from the body, so far away that in perspective the body becomes a very small speck in the middle of the domain enclosed by the closed curve.
Answers
The Kutta-Joukowski theorem, which is represented by equation (3.140), was originally derived for the case of a lifting cylinder. However, it can also be applied to a two-dimensional body of arbitrary shape, as stated in section 3.16.
A more detailed explanation of the answer.
To make a physical argument for this generalization, we can draw a closed curve around the body.
The key is to draw the curve far enough away from the body such that the body appears as a very small speck in the middle of the domain enclosed by the closed curve.
By doing this, we are essentially treating the body as a point object at the center of the curve. Since the body is now a very small speck in comparison to the large domain, its specific shape becomes insignificant to the overall flow around it.
Therefore, the lifting force calculations derived from the Kutta-Joukowski theorem for the lifting cylinder should also apply to the two-dimensional body of arbitrary shape, as long as the body is small in comparison to the domain enclosed by the closed curve.
This physical argument allows us to accept that equation (3.140) can be applied in general to a two-dimensional body of arbitrary shape without requiring a mathematical proof.
Learn more about Kutta-Joukowski theorem.
brainly.com/question/15454204
#SPJ11
There are 5 Germans and 5 Italians in an English class. If a group of 3 is going to be created, what is the probability that everyone in the group
is Italian?
A. 83%
B. 8.3%
C.10
D. 12%
Answers
Answer:
Im pretty sure its A. 83%
Step-by-step explanation:
8. The table shows how many pages Andy reads. Does Andy read at a
constant rate? Explain.
20
30
40
10
50
Time (min), x
9
4
10.
15
20
Pages, y
34
Answers
Rates are used to show how a quantity measures over another.
Andy does not read at a constant rate.
The table is given as:
\(\left[\begin{array}{cccccc}x&10&20&30&40&50\\y&4&9&10&15&20\end{array}\right]\)
Pick any two points from the table:
\((x_1,y_1) = (10,4)\)
\((x_2,y_2) = (20,9)\)
The rate (m) is then calculated as:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
So, we have:
\(m = \frac{9-4}{20-10}\)
\(m = \frac{5}{10}\)
\(m = 0.5\)
Pick another point from the table
\((x_1,y_1) = (10,4)\)
\((x_2,y_2) = (30,10)\)
The rate (m) is then calculated as:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
\(m = \frac{10 - 4}{30 - 10}\)
\(m = \frac{6}{20}\)
\(m = 0.3\)
The rates calculated are not equal
i.e. 0.3 and 0.5 are not equal
This means that;
Andy does not read at a constant rate.
Read more about rates at:
https://brainly.com/question/13103052
Jenny is making jewelry craft kits. She purchases 3 bags of each color band. She divides the total number of bands equally into 4 kits. How many bands are in each kit?
Answers
Answer:
12
Step-by-step explanation:
Given:
3 bags of each color band
4 kits
To "divide equally" we need the greatest number that divides the two numbers 3 and 4 equally.
Find the greatest common factor of 3 and 4:
factors of 3 = 1,3,6,9,12,15,18,21,24....
factors of 4 = 1,2,4,8,12,16,20,24...
How many bands are in each kit?
12 or any other number that is a factor of both 3 and 4 such as 24,..etc.