Given b(x) = |x+4|, what is b(-10)?
A) -10
B) -6
C) 6
D) 14
Answers
Answer:
b
Step-by-step explanation:
.because -10 plus 4 is -6
Related Questions
What is the equation of the line that passes through the point (−3,4) and has a slope of −2?
Answers
Answer:
y=−2x−2
Step-by-step explanation:
Which of the following is equivalent to 125%
7\4
0.125
5/4
1.025
Answers
\(\huge\boxed{\boxed{\bold{\frac{5}{4}}}}\)
\(\hrulefill\)
Let's start by finding \(125\%\) in decimal form. To do this, just divide the percentage by \(100\):
\(125\div100=1.25\)
This doesn't match any of our choices, so we'll try fraction form.
A percentage in fraction form is just the percentage over a denominator of \(100\).
\(\frac{125}{100}\)
Now we divide both the numerator and denominator by their greatest common factor, which is \(25\):
\(\frac{125\div25}{100\div25}=\large\boxed{\frac{5}{4}}\)
7.) Thazzie solved 5 math problems while Zhaniyah finished all the remaining 8problems. What percent of the math problems was Thazzie able to solve?
Answers
ANSWER:
38.46%
STEP-BY-STEP EXPLANATION:
Given:
Problems solved by Thazzie: 5 problems
Problems solved by Zhaniyah: 8 problems
Which means that there are 13 problems in total.
Therefore, those 5 represent the following percent:
\(\begin{gathered} p=\frac{5}{13}\cdot100 \\ \\ p=38.46\% \end{gathered}\)Therefore, it represents 38.46% of the problems solved by Thazzie
Make x the subject of the formula.
y = √x² +1
Answers
Answer: x = \(\sqrt{y^2 -1}\)
Step-by-step explanation:

________ refers to the pattern of covariation that is constant around the regression line, whether the values are small, medium, or large.
Answers
Homoscedasticity refers to the pattern of covariation that is constant around the regression line, whether the values are small, medium, or large.
Regression line is defined as the line which is used to estimate the unknown relationship between two variables and the relationship is linear.
The equation of this line is used to find or predict the value of one of the variable from the other.
Homoscedasticity is something which assumes that the variances are equal for different groups.
So, this refers to the pattern of covariation that is constant around the regression line, whether the values are small, medium, or large.
Hence the correct term is Homoscedasticity.
Learn more about Homoscedasticity here :
https://brainly.com/question/11097822
#SPJ1
PLEASE HELP
Lanny goes to the bank and puts $4000 in a savings account. He earns a simple interest of 2.5%. If he leaves the money in the account for five years, what is the total amount in the account after the five years?
Answers
The total amount in the account after interest will be about $4525.63 .
In the fields of finance and economics, interest is the additional sum that is paid by a borrower or deposit-taking financial institution to a lender or depositor at a certain rate (the amount borrowed).
The borrower may be obliged to pay fees to the lender or another entity, but interest is different.Interest also differs from a dividend, which is money given to shareholders (owners) by a company from its profit or reserve but not at a set rate or proportionally;It is a share of the reward or interest received by risk-taking businesspeople when income is generated that exceeds all expenses.Interest when the principal is $4000 , time is 5 years and rate is 2.5%.
We know that from compound interest:
Amount = principal (1 + rate)ⁿ
Therefore
Amount = 4000 (1 +0.025)⁵
Amount = $4525.6328...
Amount ≈ $4525.63
Therefore adding interest the sum would be worth $657.51
To learn more about interest visit:
https://brainly.com/question/13324776
#SPJ1
Help i will give brainlyest

Answers
Answer: 4
Step-by-step explanation:
a) A small island 210 square miles contain 15 species, the slope curve of species area curve for these species is 0.60 on a log-log plot. all else is being equal how many species would you expect to find on an island of 70,000 square miles?
b) there is a island area of 7000 square kilometer and that provide good habitat for peaches. the fitted constant z has been calculated 0.6. suppose that the island suddenly grows to a size of 19000 square kilometer and once it equilibrates conatin 210 species of peaches. how many species of figs would you estimate had been on the island orignially?
Answers
a) S' be the number of species on the larger island. We have S' = c * (70,000)^0.6 =489.57. b) F be the number of species of figs on the original island. F = c * (7,000)^0.6= 115.18. Solved as follows:
a) The species-area relationship, also known as the species-area curve, can be described by the equation S = cA^z.
Where S is the number of species, A is the area, c is a constant, and z is the slope of the curve on a log-log plot. Given that the slope is 0.60, we can use this information to estimate the number of species on an island of 70,000 square miles.
Calculate the constant c: Since the curve has a slope of 0.60, we know that c = S / A^z. Using the given values, c = 15 / 210^0.6 = 0.606.
Substitute the values into the equation: Now we can use the estimated constant c and the area of 70,000 square miles to find the expected number of species. Let S' be the number of species on the larger island. We have S' = c * (70,000)^0.6 =489.57.
b) To estimate the number of species of figs on the island originally, we can use the same species-area relationship and the given information about peaches on the island.
Calculate the constant c: Using the equation S = cA^z and the values S = 210 (species of peaches) and A = 19,000 square kilometers (equilibrated island size), we can solve for c: c = S / A^z = 0.568.
Estimate the number of species of figs: Let F be the number of species of figs on the original island. Using the estimated constant c and the original area of 7,000 square kilometers, we have F = c * (7,000)^0.6= 115.18.
By substituting the values into the respective equations, we can estimate the number of species for each scenario.
To learn more about log-log plot click here:
brainly.com/question/30287848
#SPJ11
In the past twenty years, scientists have seen the sea level rise at a rate of approximately 0.13 inches per year. If this rate continues, which best represents the change in sea level over the next 27 months (2.25 years)?
–2.925 inches
–0.2925 inches
0.2925 inches
2.925 inches
Answers
Answer: C or the third choice 0.2925
I just took the test I got it right!
Step-by-step explanation:
You multiply 0.13 by 2.25
0.13×2.25=0.2925
Answer:
The answer is c
Step-by-step explanation:
I just did a quiz.
How do you solve #10?

Answers
We see that since they are congruent triangles, their corresponding sides are also equal.
-> 2x + 1 = x + 3.
-> x + y = 3x - 3y
From the first equation, we can solve for x ;
2x + 1 = x + 3
Minus both sides by 1 :
2x = x + 2
Finally, minus both sides by x :
x = 2.
We substitute the value of x = 2 into the second equation :
2 + y = 6 - 3y
Add both sides by 3y :
2 + 4y = 6
Solve for y : 4y = 4 -> y = 1.
a jury pool consists of 30 people, 16 men and 14 women. compute the probability that a randomly selected jury of 12 people is all male.
Answers
The probability that a randomly selected jury of 12 people is all male is 2.1 × 10⁻⁵.
What is the probability?
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a proposition is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
An order does not matter so it is a Combination.
There are 16 men and we are going to choose 12 --> ₁₆C₁₂
There are 30 people and we are going to choose 12 --> ₃₀C₁₂
₁₆C₁₂ / ₃₀C₁₂
\(= \frac{16!}{(16 - 12)!} \div \frac{30!}{(30 - 12)!}\)
= 0.00002104211
= 2.1 × 10⁻⁵
Hence, the probability that a randomly selected jury of 12 people is all male is 2.1 × 10⁻⁵.
To learn more about the probability visit,
https://brainly.com/question/24756209
#SPJ4
Select all the lines in the proof of △ABC≅△CDA that have the correct justification. AB || CD and BC || AD, ASA Triangle Congruence Theorem ∠BAC≅∠DCA, Alternate Interior Angles Theorem △ABC≅△CDA, SAS Triangle Congruence Theorem ∠ACB≅∠CAD, Alternate Interior Angles Theorem AC≅AC, Reflexive Property of Congruence
Answers
Answer:
AB and MN
∠B and ∠N
CB and LN
Step-by-step explanation:
edg
Tanya went to the store and bought a box of spaghetti noodles for $4. She also bought x pounds of ground beef for $3.52 per pound. The total amount of money Tanya spent can be represented by the equation 18 = 3.52x + 4. How many pounds of ground beef did Tanya buy?
Answers
Answer:
Answer is in the attached photo.
Step-by-step explanation:
SolutionThe solution is in the attached photo, do take note for this question, we will have to make x the subject and solve for x.

x is equal to 3.97
What is the equation of the graphed line?
y = -x - 3
y = x + 4
y = -x - 6
y = -x + 3

Answers
Answer:
\(y=-x-3\)
Step-by-step explanation:
From the graph, we observe that the y-intercept of the line is c=-3.
So, the equation of the line is, where m is the slope:
\(y=mx+c= > y=mx-3---(1)\)
Since the line contains the point (x,y)=(-3,0), substitute x=-3 and y=0 into (1):
\(0=m(-3)-3\\0=-3m-3\\3m=-3\\m=-\frac{3}{3}= > m=-1---(2)\)
Substitute (2) into (1), and we get:
\(y=-x-3\)
Riddle
I AM THE SON OF WATER BUT WHEN I RETURN TO WATER I DIE.
WHO AM I…?
can some one help
Answers
Answer:
I am the son of waterbut when I return to water I die
Ice
Perform the indicated multiplication if possible. (Enter NONE in any unused answer blanks. If the matrices cannot be multiplied, enter NONE in each answer blank.) 7 -5 2 -9 2 - 7 1 -3 2 -10 10 [1 110]
Answers
The given matrices are a 3x2 matrix and a 2x1 matrix, which means they can be multiplied. To perform the multiplication, we need to multiply the corresponding elements in each row of the first matrix with the corresponding elements in each column of the second matrix and add the products.
The resulting matrix will be a 3x1 matrix, which means it will have 3 rows and 1 column.
Performing the multiplication, we get:
[7 -5] [1] [(7x1) + (-5x2)] [(-5)]
[2 -9] x [2] = [(2x1) + (-9x2)] = [-16]
[1 -3] [10] [(1x1) + (-3x2)] [-17]
Therefore, the resulting matrix is:
[ 1 ]
[-16]
[-17]
So, the answer to the given problem is:
[ 1 ]
[-16]
[-17]
To know more about matrix visit:-
https://brainly.com/question/29132693
#SPJ11
Ming had a box of chalk in her backpack.While walking home from school, shedecided to draw a chalk line on thesidewalk all the way to her house. The firstpiece of chalk lasted for two-thirds of ablock. If she had 11 more pieces of chalkin the box, for how many blocks in all wasshe able to draw a line?lloublocksif
Answers
In order to find how many blocks she was able to draw a line, we can calculate the following rule of three:
\(\begin{gathered} \text{chalk}\to\text{blocks} \\ 1\text{ piece}\to\frac{2}{3}\text{ block} \\ 12\text{ pieces}\to x\text{ blocks} \end{gathered}\)Now, we can write the following equation and solve it for x:
\(\begin{gathered} \frac{1}{12}=\frac{\frac{2}{3}}{x} \\ x\cdot1=\frac{2}{3}\cdot12 \\ x=\frac{24}{3} \\ x=8 \end{gathered}\)Therefore she would be able to draw a line in a total of 8 blocks.
Principal Time. Rate
$470. 10 days. 9%
Whats the interest?
Answers
Interest be I
If interest is daily
I=PRT/100I=470(10)(9)/100I=4230/10I=423$If interest is monthly (30days)
I=(470)(1/3)(9)/100I=470(3)/100I=1410/100I=14.10$Answer:
$ 1.20
Step-by-step explanation:
\(\sf Time = 10 \ days = \dfrac{10}{365}=\dfrac{2}{73}\)
\(Interest = Principal * time *rate\\\\\\=470*\dfrac{2}{73}*\dfrac{9}{100}\\\\= 1.20\)
= $ 1.20
10. If R is the midpoint of QS, find QS.

Answers
Statement:
R is the midpoint of QS.
To find out:
The measure of QS.
Solution:
QR + RS = QSSince R is the midpoint of QS, then QR = RS.QR = 2x + 16, RS = 5x - 17.Therefore, 2x + 16 = 5x - 17or, 2x - 5x = -17 - 16or, -3x = -33or, x = -33 ÷ -3or, x = 11Therefore, QR = 2(11) + 16= 22 + 16 = 38So, QS = 2QR = 2 × 38= 76Answer:
QS is 76.
Hope you could understand.
If you have any query, feel free to ask.
After reading the question what is the inequality equation and its shaded graph?

Answers
Let x represent the age of a person.
From the information given, a person must be at least 2 years old. This means that the person must be greater than or equal to 2 years. The inequality symbold representing greater than or equal to is '≥'
Thus, the inequality is
x ≥ 2
The graph would be a vertical line passing through x = 2 and the shaded area would be to the right of the line. The line would be solid, indicating that the points on the line are inclusive. Thus, the correct graph is
Four friends get the lunch special at a restaurant and leave a $3 tip. The total amount paid was $26.00. How much does the lunch special cost?
Answers
Answer:
23 dollars
Step-by-step explanation:
26 is the total with tax, so subtract the tax to get the lunch by itself
Answer:
it's 5.75
Step-by-step explanation:
first i subtracted 3$ from 26.00 and got 23.00 then i divide 23.00 by 4 and got 5.75 so that's what they payed
Allister's father is 120% of Allister's height
Answers
If Allister’s father measures 180 cm, then the height of Allister would be 150 cm
Let us assume that 'h' represents the height of Allister and 'm' represents the height of Allister’s father.
Here, Allister’s father is 120% of Allister’s height.
This means that m is 120 percent of 'h'
Using the formula of percentage,
m = 120% of h
m = 120/100 × h
m = 6h/5
But Allister’s father actually measures 180 cm
This means m = 180
so , 180 = 6h/5
We solve this equation to find the value of h.
⇒ h = 180 × 5/6
⇒ h = 150 cm
Therefore, Allister's height = 150 cm.
Learn more about percentage here:
https://brainly.com/question/16797504
#SPJ4
The complete question is:
Allister’s father is 120% of Allister’s height. If his father measures 180 cm, how tall is Allister?
Which of the following values for x and y make the equation 4x+2y+3=19 true?
Ox=5₁y=3
Ox=4,y=5
Ox=3,y=2
Ox=2,y=5
Answers
Answer:
x = 3, y = 2
Step-by-step explanation:
Substitute the values of x from each alternative in the previous question, then solve for y. This is depicted below.
A. y = -7, x = 5, 4(5) + 2y + 3 = 19B. y = 0 and x = 4, 4(4) + 2y + 3 = 19C. y = 2 and x = 3, 4(3) + 2y + 3 = 1D. y = 4, x = 2, 4(2) + 2y + 3 = 19Only the third option has a y value that is comparable to the value in the computations, according to the calculations.
As a result, the letter C is the correct response.
I know it's easy but, I'm thinking of different ways of doing it.

Answers
Answer:
9 students
Explanation:
Every 8th person that entered the cinema received a free ticket.
The number of students who entered in the first hour = 76.
The first person given a ticket was the 8th person.
To calculate the number of persons who received a free ticket, we can view this problem as an arithmetic sequence in which:
• The first term = 8
,• The last term = 76.
,• The common difference (every 8th person) = 8.
Using the formula for the last term of an arithmetic sequence, we have:
\(\begin{gathered} l=a+(n-1)d_{} \\ 76=8+8(n-1) \end{gathered}\)Our goal is to find n, the number of students.
\(\begin{gathered} 76=8+8n-8 \\ 76=8n \\ n=\frac{76}{8} \\ n=9.5 \end{gathered}\)Since the number of students that entered in the first hour is not more than 76, we have that:
\(\begin{gathered} n\le9.5 \\ \implies n=9 \end{gathered}\)9 students received a free ticket.
(a) Find the Fourier transform X (jw) of the signals x(t) given below: i. (t – 2) – 38(t – 3) ii. e-2t u(t) iii. e-3t+12 uſt – 4) (use the result of ii.) iv. e-2|t| cos(t) (b) Find the inverse Fourier transform r(t) of the following functions X(jw): i. e-j3w + e-jów ii. 27 8W - 2) + 210(w + 2) iii. cos(w + 4 7T )
Answers
i. The Fourier transform of (t - 2) - 38(t - 3) is [(jw)^2 + 38jw]e^(-2jw). ii. The Fourier transform of e^(-2t)u(t) is 1/(jw + 2). iii. The Fourier transform of e^(-3t+12)u(t-4) can be obtained using the result of ii. as e^(-2t)u(t-4)e^(12jw). iv. The Fourier transform of e^(-2|t|)cos(t) is [(2jw)/(w^2+4)].
i. To find the Fourier transform of (t - 2) - 38(t - 3), we can use the linearity property of the Fourier transform. The Fourier transform of (t - 2) can be found using the time-shifting property, and the Fourier transform of -38(t - 3) can be found by scaling and using the frequency-shifting property. Adding the two transforms together gives [(jw)^2 + 38jw]e^(-2jw).
ii. The function e^(-2t)u(t) is the product of the exponential function e^(-2t) and the unit step function u(t). The Fourier transform of e^(-2t) can be found using the time-shifting property as 1/(jw + 2). The Fourier transform of u(t) is 1/(jw), resulting in the Fourier transform of e^(-2t)u(t) as 1/(jw + 2).
iii. The function e^(-3t+12)u(t-4) can be rewritten as e^(-2t)u(t-4)e^(12jw) using the time-shifting property. From the result of ii., we know the Fourier transform of e^(-2t)u(t-4) is 1/(jw + 2). Multiplying this by e^(12jw) gives the Fourier transform of e^(-3t+12)u(t-4) as e^(-2t)u(t-4)e^(12jw).
iv. To find the Fourier transform of e^(-2|t|)cos(t), we can use the definition of the Fourier transform and apply the properties of the Fourier transform. By splitting the function into even and odd parts, we find that the Fourier transform is [(2jw)/(w^2+4)].
Learn more about exponential here:
https://brainly.com/question/29160729
#SPJ11
solve this please and tell me how you did it
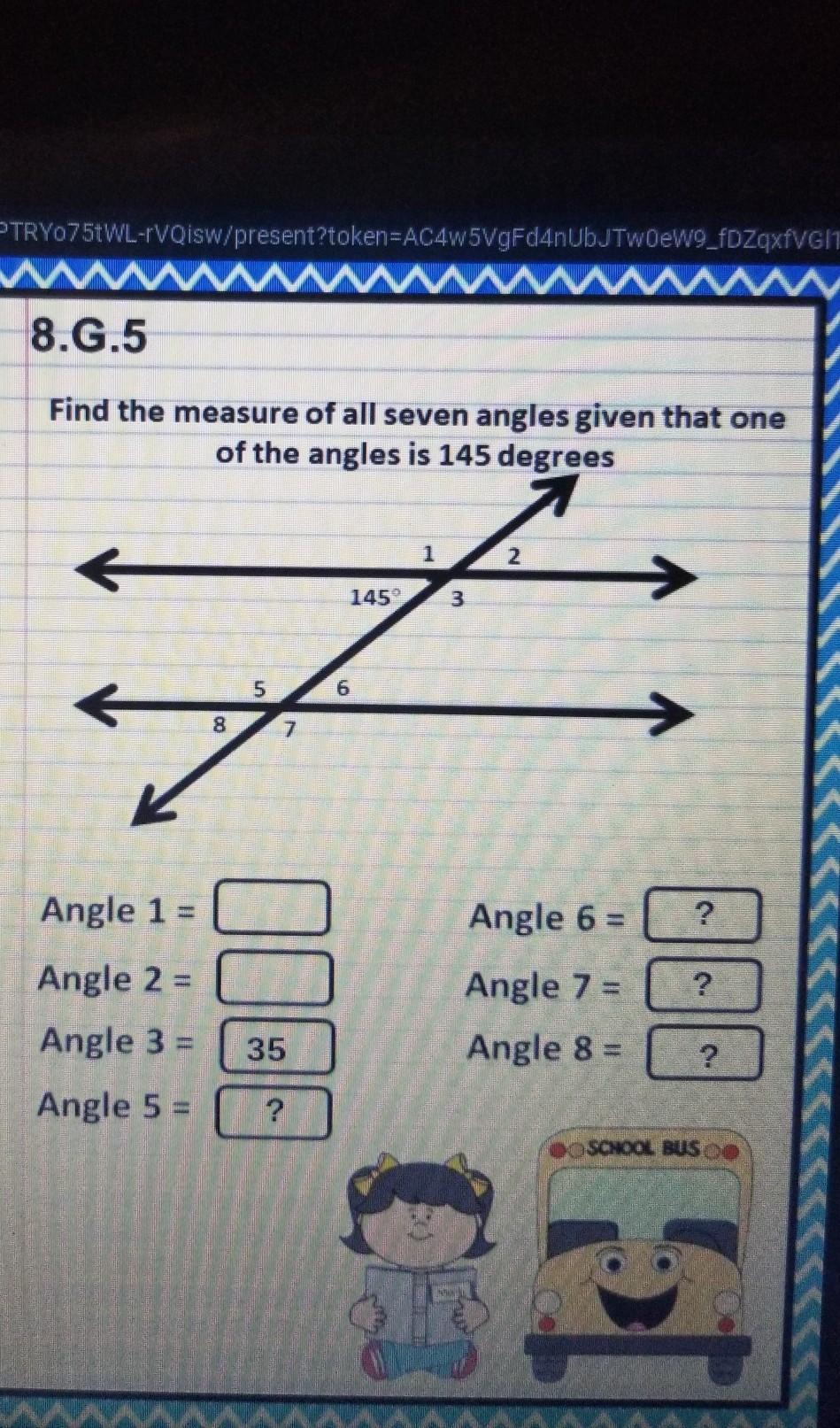
Answers
The angle ∠2 is a vertically opposite angle to the angle 145°, so they are congruent:
∠2 = 145°
The angles 1 and 3 are supplementary angles to the angle 145°, so they are equal to:
180° - 145° = 35°
∠1 = 35°
∠3 = 35°
The angle 8 is a corresponding angle to the angle 145°, so they are congruent:
∠8 = 145°
The angle ∠6 is a vertically opposite angle to the angle ∠8 so they are congruent:
∠6 = 145°
The angles 5 and 7 are supplementary angles to the angle ∠8, so they are equal to:
180° - 145° = 35°
∠5 = 35°
∠7 = 35°
Find the value of x and y and each labeled
angle.

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The required values are ~
\(\fbox \colorbox{black}{ \colorbox{white}{x} \: \: \: \: \: \: \: \: \colorbox{white}{=} \: \: \: \: \: + \colorbox{white}{40 \degree}}\)
\(\fbox \colorbox{black}{ \colorbox{white}{y} \: \: \: \: \: \: \: \: \colorbox{white}{=} \: \: \: \: \: + \colorbox{white}{80 \degree}}\)
\( \large \boxed{ \mathfrak{Step\:\: By\:\:Step\:\:Explanation}}\)
From the given figure, we can infer that ~
3x - 20° + 2x = 180°(by linear pair)
now, let's solve for x ~
\(5x - 20 \degree = 180 \degree\)\(5x = 180 \degree + 20 \degree\)\(5x = 200 \degree\)\(x = 200 \degree \div 5\)\(x = 40 \degree\)And, we can see that 2x = y (by alternate interior angle pair)
So, let's find the value of y ~
\(2x\)\(2 \times 40 \degree\)\(80 \degree\)Answer:
x = 40
3x - 20 = 100
2x = 80
y = 80
2x - 15 = 65
Step-by-step explanation:
The angles 3x - 20 and 2x are a linear pair, so they are supplementary. Their measures has a sum of 180°.
Angles 2x and y are alternate interior angles, so they are congruent.
Once we find the value of x, we can find the measure of angle 2x - 15.
3x - 20 + 2x = 180
5x = 200
x = 40
3x - 20 = 3(40) - 20 = 120 - 20 = 100
2x = 2(40) = 80
y = x = 80
2x - 15 = 2(40) - 15 = 80 - 15 = 65
A company rents out 15 food booths and 28 game booths at the county fair. The fee for a food booth is $50 plus $10 per day. The fee for a game booth is $50 plus $8 per day. The fair lasts for d days, and all the booths are rented for the entire time. Enter a simplified expression for the amount, in dollars, that the company is paid.
Answers
Answer:
$100 + $18d = payed amount
Step-by-step explanation:
Dinos really are awesome
the average of 8 girls is 15 and the average of 6 girls is 13 find the average of the other two girls with equal age
Answers
Answer:
21
Step-by-step explanation:
Since the girls have the same age, let their age be x.
Then, their average is
\(\frac{x+x}{2} = \frac{2x}{2} = x\)
Let \(S_{i}\) denote the age of 'i' girls.
Then, \(S_{8} = S_{6} + x + x - eq(1)\)
Also, we have,
\(\frac{S_{8}}{8} =15 - eq(2)\)
\(\frac{S_{6}}{6} =13 - eq(3)\)
Then eq(2):
(from eq(1) and eq(3))
\(\frac{S_{6} + 2x}{8} =15\\\\\frac{13*6 + 2x}{8} = 15\\\\78+2x = 120\\\\2x = 120-78\\\\x = 21\)
The average of the other two girls with equal age is 21
Determine the inverse Laplace transform of the function below. se - 2s 2 s+8s +41 Click here to view the table of Laplace transforms. Click here to view the table of properties of Laplace transforms. se -2s el (t) = 2 s+8s +41 (Use parentheses to clearly denote the argument of each function.)
Answers
The inverse Laplace transform of the given function is \(L^{-1}[se^{-2s}(2s^2 + 8s + 41)^{-1}] = (e^{-2t}/3) sin(4t) - (2e^{-2t}/33) (t sin(4t) + cos(4t))\)
Determination of inverse Laplace transformUse partial fraction decomposition and the Laplace transform table.
\(2s^2 + 8s + 41 = 2(s^2 + 4s + 20.5) = 2[(s+2)^2 + 16.5]\)
Using partial fraction decomposition, the Laplace transform of the given function is;
\(L{e^{-2s}} = (As + B)/(s^2 + 4s + 20.5) + (Cs + D)/(s^2 + 4s + 20.5)^2\)
Use algebraic manipulation to find the values of A, B, C, and D
Then, multiply both sides by the denominator, we have
\(e^{-2s} = (As + B)(s^2 + 4s + 20.5)^{-1} + (Cs + D)(s^2 + 4s + 20.5)^{-2}\)
Expand and equate coefficients of like terms
A = 0
B = \(e^{4}/33\)
C = 0
D =\(-2e^{4}/495\)
The Laplace transform of the function is
\(L{e^{-2s}} = (e^{4}/33)/(s^2 + 4s + 20.5) - (2e^{4}/495)/(s^2 + 4s + 20.5)^2\)
Now, we need to get the inverse Laplace transform
By using the Laplace transform table, the inverse Laplace transform of the first term is
\(L^{-1}[(e^{4}/33)/(s^2 + 4s + 20.5)] = (e^{-2t}/3) sin(4t)\)
The inverse Laplace transform of the second term is
\(L^{-1}[-(2e^{4}/495)/(s^2 + 4s + 20.5)^2] = -(2e^{-2t}/33) (t sin(4t) + cos(4t))\)
Thus, the inverse Laplace transform of the given function is
\(L^{-1}[se^{-2s}(2s^2 + 8s + 41)^{-1}] = (e^{-2t}/3) sin(4t) - (2e^{-2t}/33) (t sin(4t) + cos(4t))\)
Learn more on Inverse Laplace transform on https://brainly.com/question/31433192
#SPJ4