Answers
The standard equation of the circle is:- x²- 6x + y²+ 10y - 39 = 0
What is equation of circle ?
The equation of a circle is given by:
(x - h)²+ (y - k)² = r²
where (h, k) is the center of the circle and r is the radius. This equation represents all the points in the coordinate plane that are at a distance of r units from the point (h, k).
Center (4,1) and radius 5:
The standard equation of a circle with center (h,k) and radius r is:
(x-h)² + (y-k)² = r²
Substituting the given values, we get:
(x-4)²+ (y-1)² = 5²
Simplifying and expanding the terms, we get:
x²- 8x + y² - 2y - 8 = 0
So the standard equation of the circle is:
(x-h)² + (y-k)² = r²
Substituting the given values, we get:
(x-3)² + (y+5)²= 11²
Simplifying and expanding the terms, we get:
x²- 6x + y² + 10y - 39 = 0
So the standard equation of the circle is:
x²- 6x + y²+ 10y - 39 = 0
In geometry, a circle is a shape consisting of all the points in a plane that are equidistant from a given point called the center of the circle. The distance from the center to any point on the circle is called the radius of the circle.
A circle can be defined as the locus of all points in a plane that are at a constant distance (the radius) from a fixed point (the center). The circle is a fundamental shape in mathematics and geometry, and it appears in many different contexts, such as in the description of orbits in astronomy, the geometry of lenses in optics, and the analysis of electric fields in physics. Circles also have many applications in engineering, architecture, and other fields.
To know more about circle visit :-
https://brainly.com/question/24375372
#SPJ1
Related Questions
If f (x) = 2 x + 5 and three-halves are inverse functions of each other and StartFraction 41
Answers
The inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
What is the procedure to find inverse of function ?Inverse of a function can be calculated by following the steps mentioned below -
Step 1 - Replace {y} with {x} and vice - versa.Step 2 - Rewrite the equation by solving for {y}.Step 3 - Replace {y} with f⁻¹(x).According to the question, the equation given is as follows
y = f(x) = 2x + 5
y = 2x + 5
Replace 'y' with 'x', we get -
x = 2y + 5
Now, solve for y -
2y = x - 5
y = (x/2) - (5/2)
Replace 'y' with f⁻¹(x) -
f⁻¹(x) = (x/2) - (5/2)
Hence, the inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
To solve more questions on inverse of function, visit the link below-
brainly.com/question/28229665
#SPJ1
Which mixed numbers have 12 as the LCD (lowest common denominator)?
2 11/12
3 1/7
5 3/4
6 4/5
8 38
MARK
Answers
The mixed numbers that have 12 as the LCD are 2 11/12 and 6 4/5. All other fractions do not have 12 as the denominator and are not equivalent.
What are mixed numbers?Mixed numbers consist of a whole number and a fractional part. To add or subtract mixed numbers, the fractions must have the same denominator (the bottom number of the fraction).
The LCD (lowest common denominator) is the smallest number that all of the denominators can be divided into evenly. In this case, the LCD is 12.
2 11/12 and 6 4/5 both have 12 as the denominator. The denominator of 11/12 can be divided by 11 and 12, so it is the same as 12/12. The denominator of 4/5 can be divided by 4 and 12, so it is the same as 48/12 (4 x 12 = 48). Therefore, both fractions have the same denominator.
The other fractions do not have 12 as their denominator. 3 1/7 can be divided by 3, 7, and 12, so it is the same as 21/12 (3 x 7 = 21). 5 3/4 can be divided by 4, 5, and 12, so it is the same as 60/12 (4 x 5 = 60). 8 38/47 can be divided by 8, 47, and 12, so it is the same as 376/12 (8 x 47 = 376). Since none of these fractions are equal to 12/12, they are not equivalent to the other two fractions.
For more questions related to fractions
https://brainly.com/question/28699958
#SPJ1
Question :
Which mixed numbers have 12 as the LCD (lowest common denominator)?
2 11/12
3 1/7
5 3/4
6 4/5
8 38/47
How do you write a point slope form equation from this graph?

Answers
Answer: y-1=3(x-3)
this in the correct answer. you take one point on the line and substitues x and y of the point into the equation. M is your slope. y-y1=m(x-x1)
At the local Theatre of the Arts, tickets cost $4 for children and $5 for adults. In the opening Saturday night of a play, the theater made $540. The second day was a matinee and the prices were lower for children at $3 and the same price as Saturday for adults. They made $440 at the matinee.
A) Write a system of equations in standard form that represents the prices at the Theatre on Saturday and the second day.
B) Rewrite the system of equations in slope-intercept form. What are the y-intercepts of both equations?
Answers
A. The system of equations in standard form is: 4x + 5y = 540 and 3x + 5y = 440.
B. The y-intercept of the equation representing the prices on Saturday night is 108, and the y-intercept of the equation representing the prices at the matinee on the second day is 88.
A) Let's define the variables:
Let x represent the number of children attending.
Let y represent the number of adults attending.
On Saturday night:
The equation for the revenue generated on Saturday night is:
4x + 5y = 540 (since children's tickets cost $4 and adults' tickets cost $5, and the total revenue is $540).
Matinee on the second day:
The equation for the revenue generated at the matinee is:
3x + 5y = 440 (since children's tickets cost $3 and adults' tickets still cost $5, and the total revenue is $440).
Therefore, the system of equations in standard form is:
4x + 5y = 540
3x + 5y = 440
B) Let's rewrite the system of equations in slope-intercept form:
On Saturday night:
4x + 5y = 540
Rearranging the equation, we get:
5y = -4x + 540
Dividing both sides by 5, we get:
y = (-4/5)x + 108
The y-intercept of this equation is 108.
Matinee on the second day:
3x + 5y = 440
Rearranging the equation, we get:
5y = -3x + 440
Dividing both sides by 5, we get:
y = (-3/5)x + 88
The y-intercept of this equation is 88.
For such more question on equation:
https://brainly.com/question/17145398
#SPJ8
Hiking
(15,18
(10, 12)
Distance (miles)
15,6
10
15
Time
Using the data shown on the graph, which sztements are correct?
The
3
The ratio of L is consistent
The graph represents a proportional relationship
D
The grach does not represent a proportional relationship
The graph of a proportional relationship must past through. (0,0)
Answers
Answer:
I’m sorry but I don’t understand the question
Step-by-step explanation:
If
to DEF?
A 23
B. 16°
C. 32°
D. 58°
Answers
The calculated measure of the angle D is (c) 32 degrees
How to determine the measure of the angleFrom the question, we have the following parameters that can be used in our computation:
The triangles ABC and DEF
The triangles are similar triangles
This means that the corresponding angles are equal
Given that
A = 32 degrees
And the corresponding angle is D
We have
D = 32 degrees
Hence, the measure of the angle is (c) 32 degrees
Read more about angles at
https://brainly.com/question/31898235
#SPJ1

12. Find the values of x and y in the diagram below.

Answers
Answer:
x = 15
y = 19
The value of the x and y are; 11/6, -5 and 18/4 in the linear equation.
What is linear equation?The definition of a linear equation is an algebraic equation in which each term has an exponent of one and the graphing of the equation results in a straight line.
From the given parameters;
The equations are;
(4y - 18)
(6x - 11)
(x + 5)
Now put all equation equal to zero.
Then;
4y - 18 = 0
y = 18/4
And then;
6x - 11 = 0
x = 11/6
And
x + 5 = 0
x = -5.
Hence, In the linear equation, value of the x and y are 11/6, -5 and 18/4.
Learn more about linear equation here;
brainly.com/question/4074386
#SPJ2
some adults and children are watching a musical there are n children there are 25 fewer adults
Answers
According to the concept of algebraic expression and arithmetic, the correct answers are A) Number of adults = N - 25. B) Number of adults when N = 124: 124 - 25 = 99
A) Let's denote the number of children as N. Since there are 25 fewer adults than children, the number of adults can be expressed as N - 25.
B) If there are 124 children, we substitute N with 124 in the expression from part A. Thus, the number of adults would be 124 - 25 = 99.
To arrive at these answers, we used the given information that there are "N" children and 25 fewer adults than children. By substituting the value of N, we determined the number of adults in terms of N and then calculated the specific number of adults when N is equal to 124.
Note: The given question is incomplete. The complete question is:
Some adults and children are watching a musical. there are 'N' number of children. There are 25 fewer adults than children.
A) find the number of adults in terms of 'N'.
B) if there are 124 children how many adults are there?
For more questions on algebraic expression:
https://brainly.com/question/29333936
#SPJ8
Devi invested a principal of $2750 in her bank account with an interest rate of 1.5%. How much simple interest did she earn in 3 years?
Answers
To calculate the simple interest, we use the following formula:
(Principal) • (interest rate) • (time) = simple interest
Plugging the values in, we will find that:
$2,750 (our principal) • 0.015% (our interest rate represented by a decimal) • 3 (our time period in years) = $123.75 (our simple interest)
Ultimately, Devi made an investment and in 3 years earned a simple interest of $123.75.
A soccer player has a large cylindrical water cooler that measures 3 feet in diameter and is 4 feet tall. If there are approximately 7.48 gallons of water in a cubic foot, how many gallons of water are in the water cooler when it is completely full? Use π = 3.14 and round to the nearest hundredth. 28.26 gallons 113.04 gallons 211.38 gallons 845.54 gallons
Answers
The volume of the cylindrical water cooler is 211.38 gallons. Therefore, option C is the correct answer.
What is the volume?Volume is the measure of the capacity that an object holds.
Formula to find the volume of the object is Volume = Area of a base × Height.
Given that, a soccer player has a large cylindrical water cooler that measures 3 feet in diameter and is 4 feet tall.
Now, radius = 3/2 =1.5 feet
We know that, the formula to find the volume of a cylinder is πr²h.
Here, 3.14×1.5²×4
= 28.26 cubic feet
In gallons = 28.26×7.48
= 211.38 gallons
Therefore, option C is the correct answer.
To learn more about the volume visit:
https://brainly.com/question/13338592.
#SPJ1
The correct option is C, 211.38. Hope this helps :)
the sum of twice a number and five is 11 . find the number?
Answers
Solution
Let the number be represented by x
\(2x+5=11\)Now, solve x
\(\begin{gathered} 2x=11-5 \\ 2x=6 \\ divide\text{ both sides by 2} \\ \frac{2x}{2}=\frac{6}{2} \\ \\ x=3 \end{gathered}\)The final answer
The number is 3
\(x=3\)he polynomial of degree 5, P ( x ) has leading coefficient 1, has roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 Find a possible formula for P ( x ) .
f]
Answers
The possible formula for the polynomial in discuss whose roots are described as; having roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 is; P(x) = x^5 -5x⁴-6x³+18x².
What is the polynomial in discuss whose roots and leading coefficient are as discussed?The polynomial which is as described in the task content whose roots are as given can be written in its factorised form as follows;
P(x) = (x-3) (x-3) (x) (x) (x+1)
The expanded form is therefore;
P(x) = x^5 - 5x⁴- 6x³+ 18x².
Therefore, the polynomial having roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 is P(x) = x^5 - 5x⁴- 6x³+ 18x².
Read more on polynomials;
https://brainly.com/question/13793580
#SPJ1
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
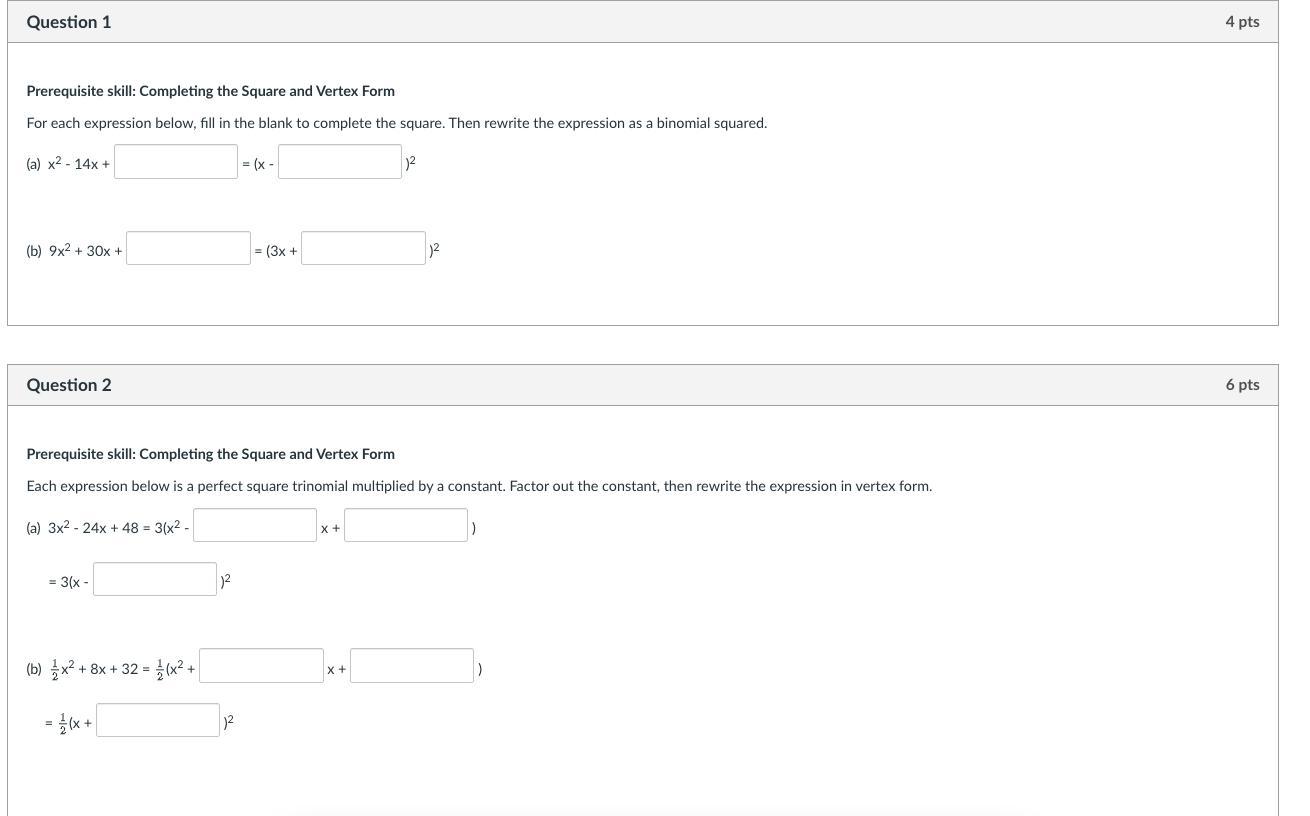
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Merry Christmas, I have a riddle for you.
Who has a popular Christmas song titled with his name,
He looks pretty normal unless you look at his nose.
Answers
Enola is saving money and plans on making monthly contributions into an account
earning a monthly interest rate of 0.4%. If Enola would like to end up with $5,000
after 3 years, how much does she need to contribute to the account every month, to
the nearest dollar? Use the following formula to determine your answer.
Answers
Enola needs to contribute $4,330.68 per month to the account.
How much does Enola need to contribute to the account?Let's denote the monthly contribution as X.
The interest rate is 0.4% per month.
Since Enola plans to save for 3 years, the total number of months is:
= 3 * 12
= 36 months.
Using formula for compound interest: Future value = Present value * (1 + interest rate)^number of periods
We will plug values:
$5,000 = X * (1 + 0.004)^36
X = $5,000 / (1 + 0.004)^36
X = $5,000 / (1.004)^36
X = $4,330.68248
X = $4,330.68.
Need help fast please help me as quickly as possible

Answers
Shipping rates for Company A and Company B are shown in the tables below. Which company has shipping rates that you can represent using an equation of the form y = kx?
Answers
Answer:
OMG I KNOW THE ANSWER!!!!!!!!
Step-by-step explanation:
its b.
Answer:
company b
Step-by-step explanation:
2. The holding tanks are congruent in size, and both are in the shape of a cylinder that has been cut in half vertically. The bottom of the tankis a curved surface. What is the volume of both tanks if the radius of tank #1 is 15 feet and the height of tank #2 is 120 feet? You mustexplain your answer using words, and you must show all work and calculations to receive creditx

Answers
So,
Congruent tanks implies that both tanks are of identifical shape, form & dimensions. Congruent means that the tanks have the same radius as well as height. Hence, the heights and radius of tanks #1 and #2 are equal and the same.
Now:
- radius(tank #1) = 15 ft ⇒ radius(tank #2) = 15 ft
- height(tank #2) = 120 ft ⇒ height(tank #1) = 120 ft
The volume of a cylinder is given by the equation:
\(V=\pi\cdot r^2\cdot h\)As the tanks have been cut into half, we got that the volume of each tank is:
\(V=\frac{1}{2}\pi\cdot r^2\cdot h\)The volume of both tanks is the sum of the volume each one, so:
\(\text{TotalVolume=VTank1+Vtank2}_{}\)Both are cogruent so we could write:
\(\text{Total}=\frac{1}{2}\pi\cdot r^2\cdot h+\frac{1}{2}\pi\cdot r^2\cdot h=\pi\cdot r^2\cdot h\)If we replace:
\(TotalVolume=\pi\cdot(15ft)^2(120ft)=84823.002ft^3\)Find the slope of the line y= -1/3x-6
Answers
Answer:
-1/3
Step-by-step explanation:
y=mx+b where m=slope and b=y-intercept.
Connor and Maria are doing yard work for a neighbor. They make a total of $597.19. Since Maria works fewer hours than Connor, Maria gets 19% of the money. About how much (in whole dollars) does Maria make?
Answers
Answer:
$113
Step-by-step explanation:
Find 19% of $597.19:
0.19($597.19) = $113 (in whole dollars)
w/-6=20 read as w divided by -6 equals 20. what would my answer be?
Answers
From the expression: w/-6 = 20, we can solve for w, like this:
\(\begin{gathered} \frac{w}{-6}=20 \\ \frac{w}{-6}\times-6=20\times-6 \\ w\times\frac{-6}{-6}=-120 \\ w\times1=-120 \\ w=-120 \end{gathered}\)As proved, w equals -120
6. Determine the system of equations based on the following relationships and then solve
for the two integers.
a. Fourteen more than twice the first integer gives the second integer
b. The second integer increased by one is the square of the first integer
Answer: (-3,8) and (5,24)
Answers
The two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).
To solve the system of equations, let's assign variables to the two integers. Let the first integer be represented by 'x' and the second integer by 'y'.
According to the given information:
a. Fourteen more than twice the first integer gives the second integer:
This can be expressed as: 2x + 14 = y
b. The second integer increased by one is the square of the first integer:
This can be expressed as: y + 1 = x^2
Now, we have a system of equations:
1) 2x + 14 = y
2) y + 1 = x^2
To solve this system, we can substitute the value of 'y' from equation 1) into equation 2):
2x + 14 + 1 = x^2
2x + 15 = x^2
Rearranging the equation, we have:
\(x^2 - 2x - 15 = 0\)
Factoring the quadratic equation, we get:
(x - 5)(x + 3) = 0
Setting each factor equal to zero:
x - 5 = 0 --> x = 5
x + 3 = 0 --> x = -3
Substituting the values of 'x' back into equation 1), we can find the corresponding values of 'y':
For x = 5:
2(5) + 14 = y
10 + 14 = y
y = 24
For x = -3:
2(-3) + 14 = y
-6 + 14 = y
y = 8
Therefore, the two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).
for more such question on integers visit
https://brainly.com/question/929808
#SPJ8
Please explain how to solve this

Answers
The solution to the variables are x = 7 and y = 4
How to determine the solution to the variables?From the question, we have the following parameters that can be used in our computation:
Shape = Triangle
The marks on the triangles imply that
The visibly smaller triangle is an equilateral triangleThe other triangle is an isosceles triangleSo, we have the following representation
3x - 5 = 5y - 4
3x - 5 = y + 12
Substitute 3x - 5 = y + 12 in 3x - 5 = 5y - 4
y + 12 = 5y - 4
Evaluate the like terms
4y = 16
So, we have
y = 4
Substitute y = 4 in 3x - 5 = y + 12
3x - 5 = 4 + 12
So, we have
3x = 21
This gives
x = 7
Hence, the values are x = 7 and y = 4
Read more about triangles at
https://brainly.com/question/14285697
#SPJ1
Find the distance between points A = (2, 0) and
B= (0, 9). Round your answer to the nearest tenth.
Show your work
Answers
Answer:
9.2
Step-by-step explanation:
You want the distance between A(2, 0) and B(0, 9).
DistanceThe distance formula is based on the Pythagorean theorem. It tells you the distance between (x1, y1) and (x2, y2) is ...
d = √((x2 -x1)² +(y2 -y1)²)
For the given points, this becomes ...
d = √((0 -2)² +(9 -0)²) = √(4+81) = √85
d ≈ 9.2
The distance between A and B is about 9.2 units.

A light bulb consumes 15300 watt-hours in 4 days and 6 hours . How many watt-hours does it consume per day?
Answers
Answer:
3600
Step-by-step explanation:
It consumes 3600 watt hours per day. Steps are included below.
We know that there is 24 hours in a day so we times 24 by the consumes watt hours that is 15300. So 24 times 15300. After that we need to time 4 times 24+6 = the answer that is 3600. That how you get the answer.
Steps:
1: 24*15300/(4*24+6)=3600
Answer: 3600 watt hours per day
Hope this helps.
Answer:
3,600
Step-by-step explanation:
In the question, there is energy consumption and a rate but not in an easy way.
In order to find out how much watt-hours the light bulb consumes per day, the easiest way is to multiply by the hour to find out how much it uses in a day.
In 4 days and 6 hours there are 102 hours.
\(4 \times 24 = 96\)
\(96 + 6 = 102\)The hours for 4 days...
\(96 + 6 = 102\)
4 days plus 6 hours. The total time...
Now make the watt-hours usage an hourly rate...
\(15300 + 102 = 150\)
150 watts/hour...
Take the hourly rate and multiply it by 24 (number of hours in a day) to find out how many watt-hours the lightbulb uses in a day...
\(150 \times 24 = 3600\)
(05.03 MC)
Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 4x and y = 2x−2 intersect are the solutions of the equation 4x = 2x−2. (4 points)
Part B: Make tables to find the solution to 4x = 2x−2. Take the integer values of x between −3 and 3. (4 points)
Part C: How can you solve the equation 4x = 2x−2 graphically? (2 points)
(10 points)
Answers
Part A: The intersection of these two lines is (-1,-4). Since x=-1, this is also the solution to 4x=2x-2 as per the graph.
Part B: Table attached.
Part C: Graph attached.
What is a graph?Graphing a function involves tracing the curve on a coordinate plane that corresponds to the function. If the curve represents the function for the curve, then each point on the curve will satisfy the function equation. The graph below shows the linear function f(x) = -x+ 2 as an illustration.
In the question,
The expression 4x = 2x - 2 reduces to x = -1. This is true for all values of y, since y is not a factor in this expression.
The two other equations intersect at point (-1, -4). See the attached graph (Solutions2)
y = 4x
y = 2x−2
Mathematically, we can substitute the value of y from the first equation into the second:
y = 2x−2
(4x) = 2x−2
2x = -2
x = -1
The intersection of these two lines is (-1,-4). Since x=-1, this is also the solution to 4x=2x-2.
To know more about graphs, visit:
https://brainly.com/question/17267403
#SPJ1


Determine f(-1) (3). Use the following table of values

Answers
Answer:
-5
Step-by-step explanation:
The value of x that gives f(x) = 3 is -5.
\(f^{-1}(3)=-5\)
Find the volume of the figure. For calculations involving , give both the exact value and an approximation to the nearest hundredth of a unit. Let d = 10 and h = 18.
________ ft3 ≈ _________ft3
Answers
Thus, the volume of cylinder with the given height and diameter is found as 1413 ft³.
Explain about the shape of cylinder:A cylinder is three-dimensional. It's not a flat thing. There are parallel circular bases in this shape. These bases have a curved face affixed to them. A cylinder in this instance has three faces. Along both end of a curved face, which rounds back to the face's origin, are two spherical bases.
Given that-
diameter d = 10 ftRadius r = 10/2 = 5 ftHeight h = 18 ftVolume of cylinder = πr²h
Volume of cylinder = 3.14 *5²*18
Volume of cylinder = 3.14*25*18
Volume of cylinder = 1413 ft³
Thus, the volume of cylinder with the given height and diameter is found as 1413 ft³.
Know more about the cylinder:
https://brainly.com/question/23935577
#SPJ1

Construct an equation for the expression: 3 less than 2 times a number is 7. Show the solution to the equation and prove your solution to be true through your work.
Answers
Answer:
5 x 2 -3 = 7
Step-by-step explanation:
i mean.... thats all
Calculate the distance between the points (4,-2) and (7,-9)
Answers
The Distance between the points (4, -2) and (7, -9) is sqrt(58) or approximately 7.62 units.
The distance between two points in a coordinate plane. The distance formula is based on the Pythagorean theorem and calculates the straight-line distance between two points.
The coordinates of the first point as (x1, y1) = (4, -2) and the coordinates of the second point as (x2, y2) = (7, -9).
The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Plugging in the values:
d = sqrt((7 - 4)^2 + (-9 - (-2))^2)
d = sqrt((3)^2 + (-7)^2)
d = sqrt(9 + 49)
d = sqrt(58)
Hence, the distance between the points (4, -2) and (7, -9) is sqrt(58) or approximately 7.62 units.
To know more about Distance .
https://brainly.com/question/23848540
#SPJ11
